Performance Analysis of Orthogonal Multiuser Short Reference Differential Chaos Shift Keying Communication System
-
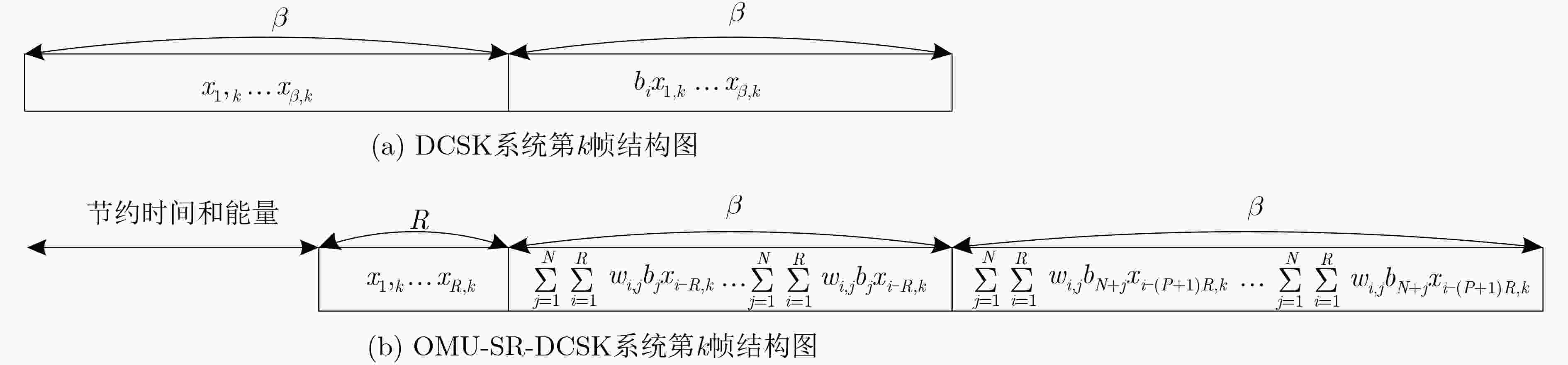
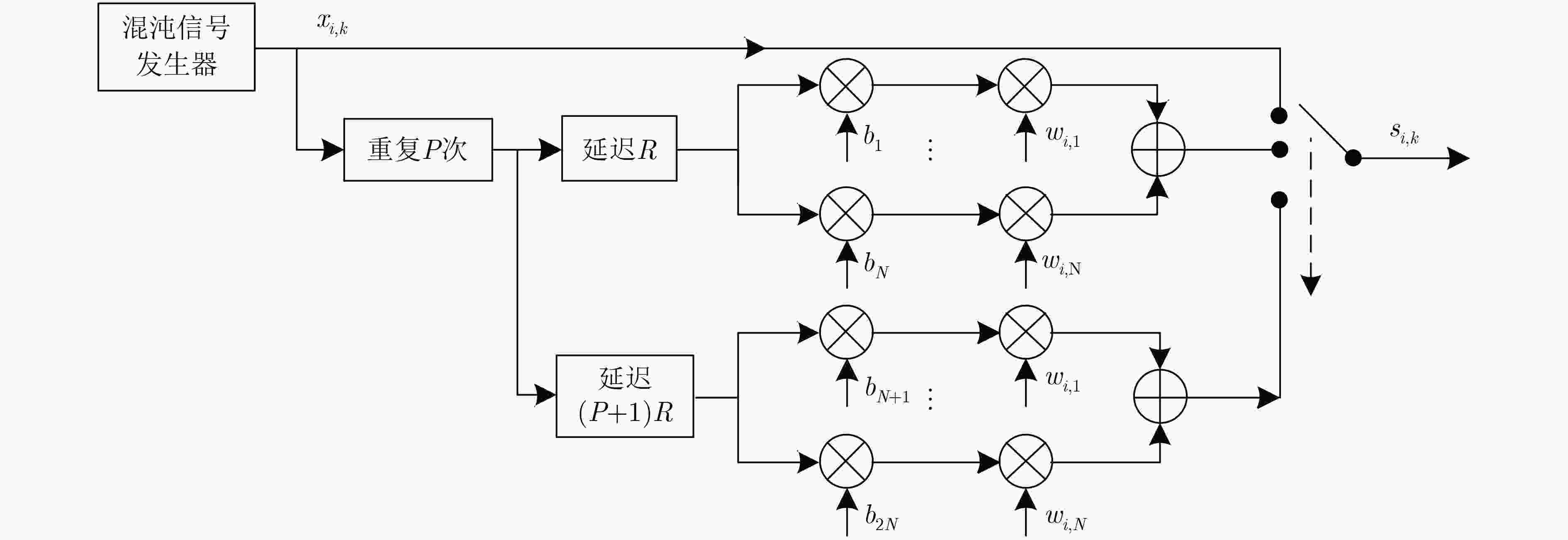
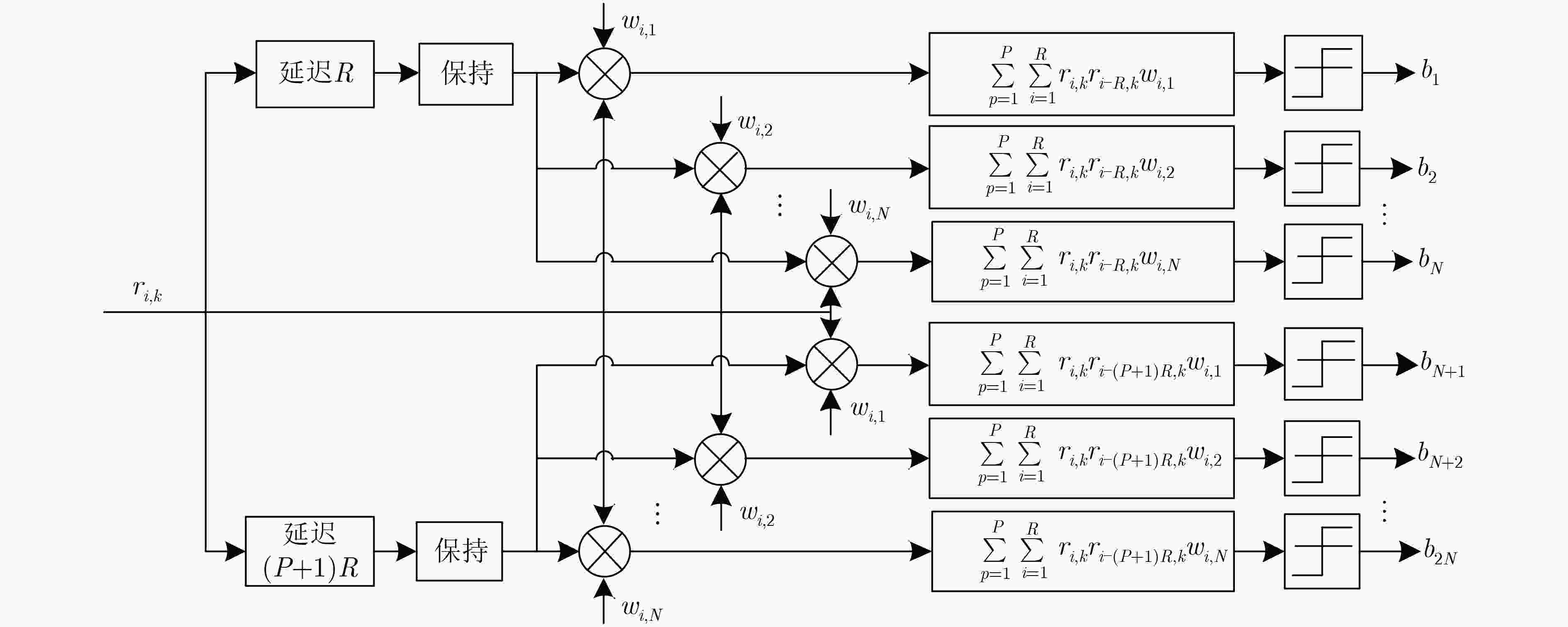
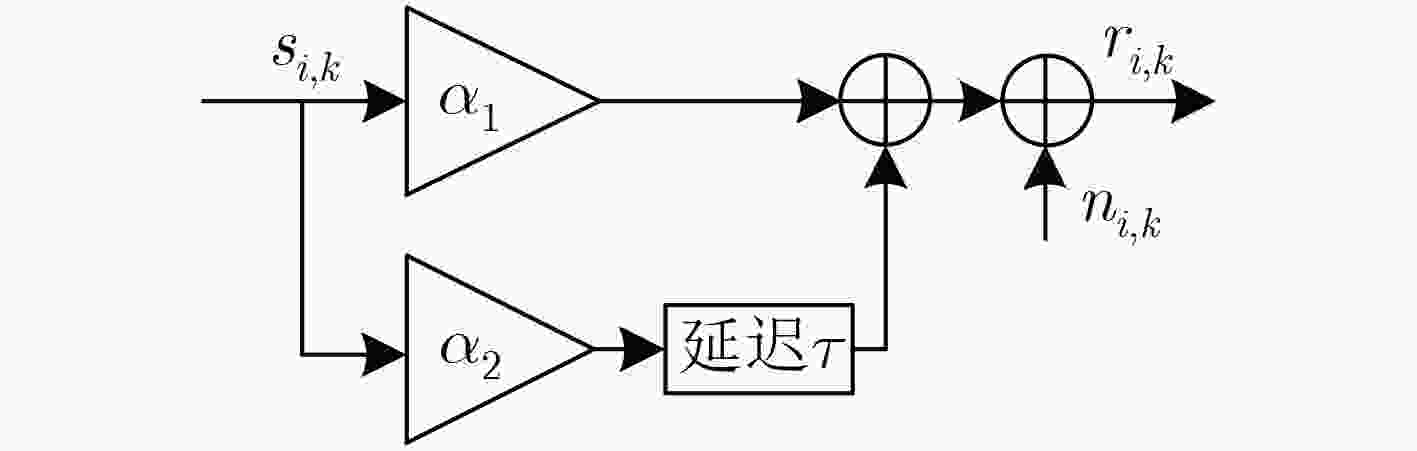
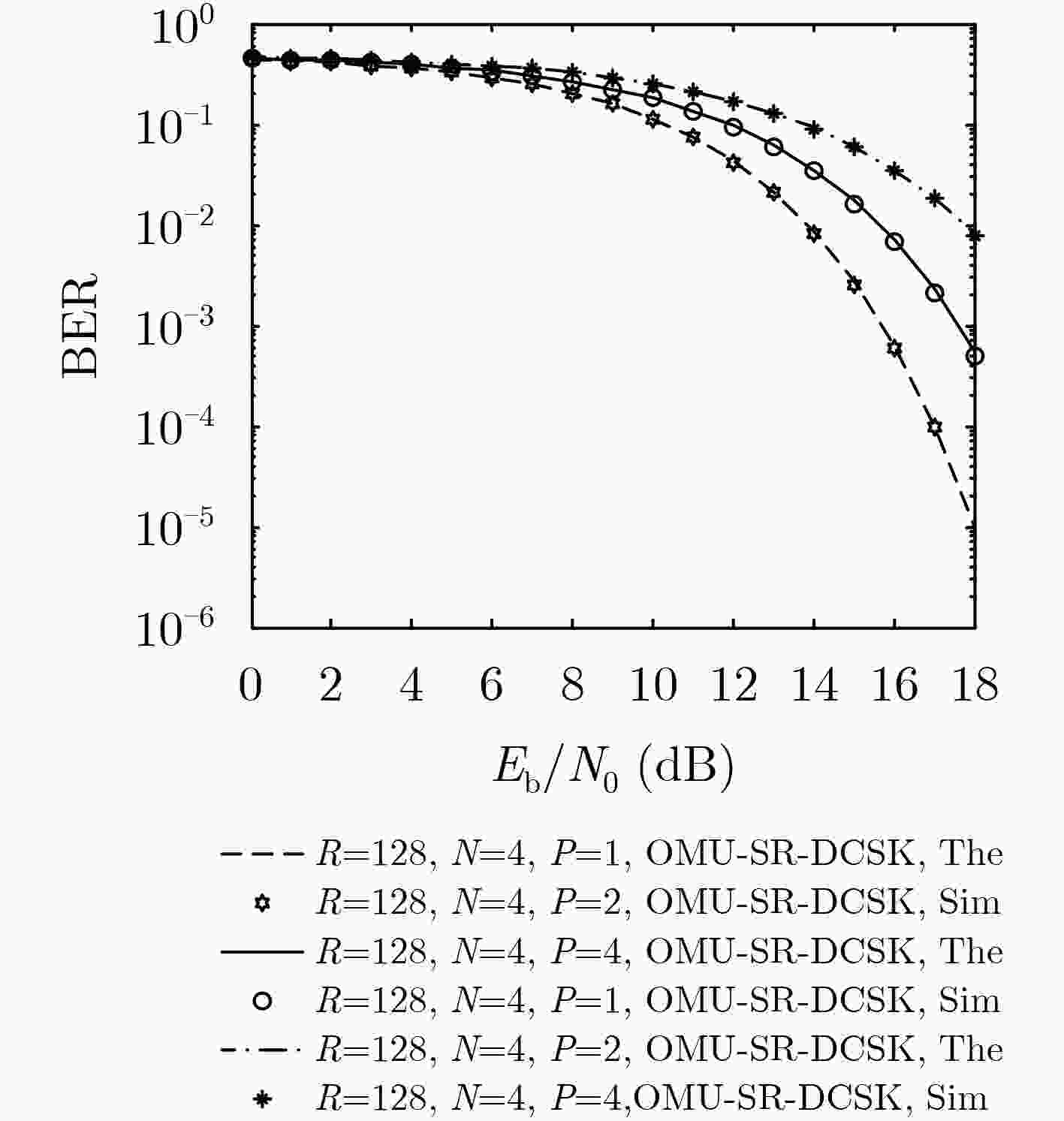
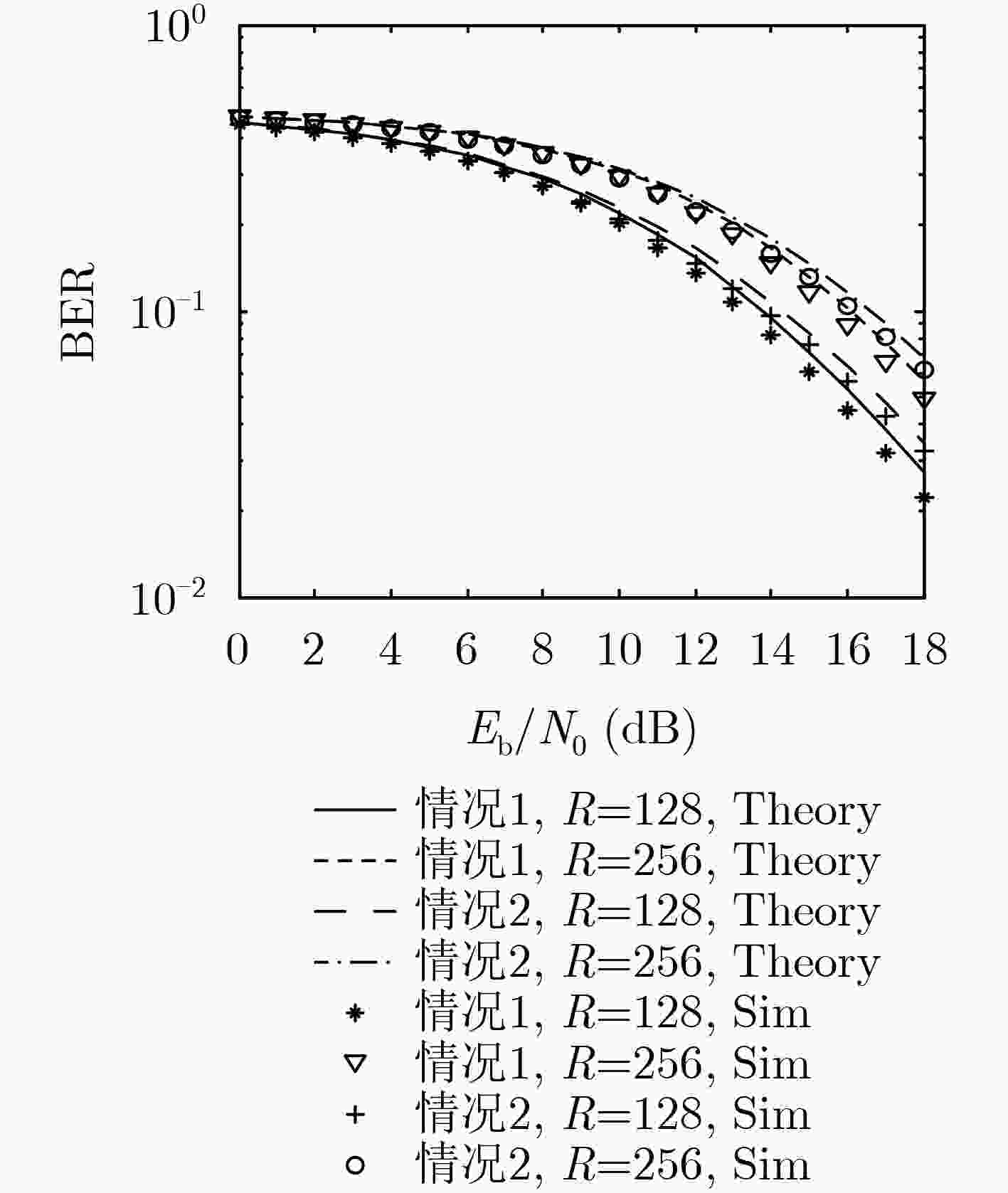
摘要: 针对差分混沌移位键控系统传输速率和能量效率低的缺点,该文提出一种正交多用户短参考差分混沌移位键控(OMU-SR-DCSK)通信系统。系统将参考信号长度缩短为每个信息承载信号长度的1/P,并在参考时隙后增加了两路连续的信息时隙,每个信息时隙内,N个用户信息在Walsh码正交特性作用下同时传输,利用Walsh码的正交特性可完全消除用户间干扰,从而改善系统误码性能。推导了OMU-SR-DCSK在加性高斯白噪声(AWGN)信道和Rayleigh衰落信道下的理论比特误码率(BER)公式并进行了仿真。仿真结果和理论推导的吻合证明了理论推导的正确性,从而为OMU-SR-DCSK应用于多用户串行传输系统提供了理论依据。Abstract: An Orthogonal MultiUser Short Reference Differential Chaos Shift Keying (OMU-SR-DCSK) communication system is proposed to overcome the dominant drawbacks of DCSK system relating to low transmission rate and energy efficiency. The proposed system shortens the reference signal to 1/P of information bearing signal. Two consecutive information time slots are added after the reference time slot. Due to the excellent features of Walsh codes, the system sends information from N users in one information time slot. Meanwhile, the use of orthogonality of the Walsh code eliminates completely intra-signal interference and enhances the performance of Bit Error Rate (BER) better. The theoretical BER formula of OMU-SR-DCSK over Additive White Gaussian Noise (AWGN) channel and Rayleigh fading channel are derived and simulations are carried out respectively. The coincidence between the simulation results and the theoretical derivations proves the correctness of the theoretical derivation, providing a theoretical basis for the application of OMU-SR-DCSK to multiuser serial transmission system.
-
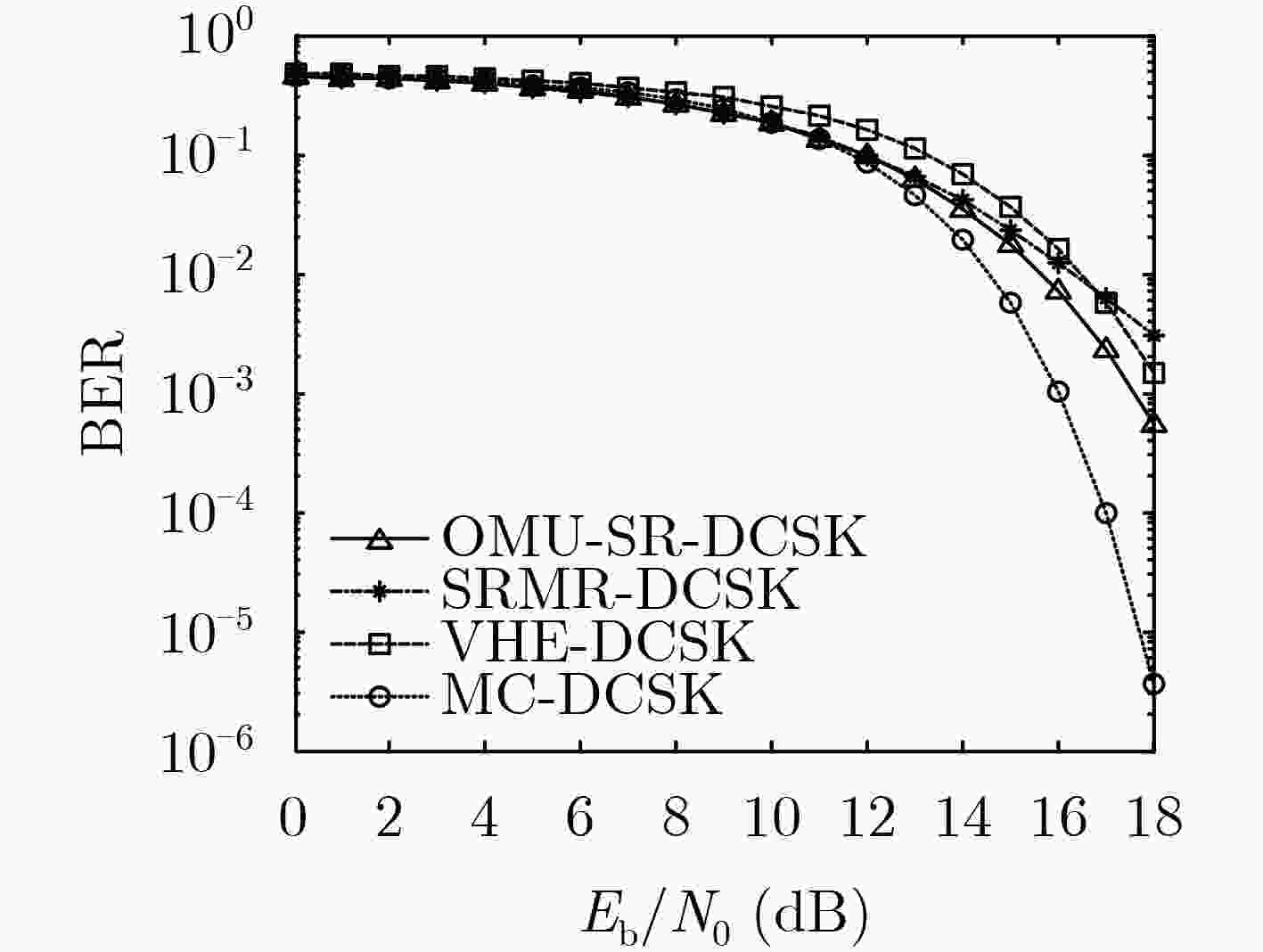
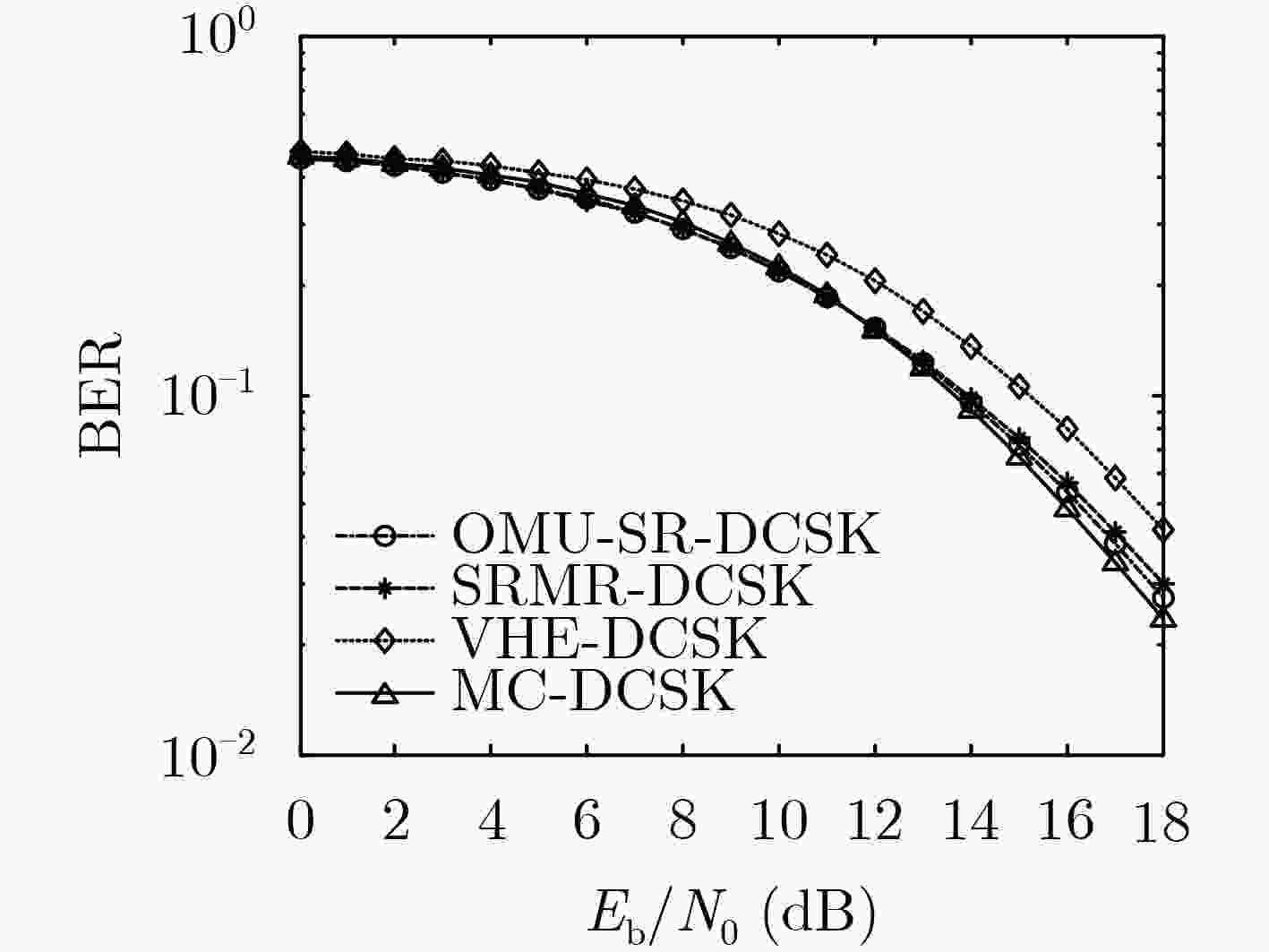
表 1 OMU-SR-DCSK, SRMR-DCSK, VHE-DCSK和MC-DCSK系统的能量效率及传输速率
系统名称 传输速率(${R_B}$) 能量效率(${E_\eta }$) OMU-SR-DCSK ${{2N} / {(R + 2\beta )}}$ ${{2N\beta } / {(R + 2N\beta )}}$ SRMR-DCSK ${N / {(R + \beta )}}$ ${{N\beta } / {(R + N\beta )}}$ VHE-DCSK ${N / {(2\beta }})$ ${N / {(1 + N)}}$ MC-DCSK ${N / \beta }$ ${N / {(1 + N)}}$ -
ÇICEK S, KOCAMAZ U E, and UYAROĞLU Y. Secure chaotic communication with Jerk chaotic system using sliding mode control method and its real circuit implementation[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2019, 43(3): 687–698. doi: 10.1007/s40998-019-00184-9 ESCRIBANO F J, KADDOUM G, WAGEMAKERS A, et al. Design of a new differential chaos-shift-keying system for continuous mobility[J]. IEEE Transactions on Communications, 2016, 64(5): 2066–2078. doi: 10.1109/TCOMM.2016.2538236 CAI Guofa, FANG Yi, HAN Guojun, et al. A new hierarchical M-ary DCSK communication system: Design and analysis[J]. IEEE Access, 2017, 5: 17414–17424. doi: 10.1109/ACCESS.2017.2740973 KADDOUM G, TRAN H V, KONG Long, et al. Design of simultaneous wireless information and power transfer scheme for short reference DCSK communication systems[J]. IEEE Transactions on Communications, 2017, 65(1): 431–433. doi: 10.1109/TCOMM.2016.2619707 HU Wei, WANG Lin, and KADDOUM G. Design and performance analysis of a differentially spatial modulated chaos shift keying modulation system[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2017, 64(11): 1302–1306. doi: 10.1109/TCSII.2017.2697456 张琳, 徐位凯, 王琳, 等. 码复用差分混沌键控性能分析与同步算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(3): 330–336.ZHANG Lin, XU Weikai, WANG Lin, et al. Performance analysis and synchronization algorithm for CS-DCSK system[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition) , 2016, 28(3): 330–336. YANG Hua and JIANG Guoping. High-efficiency differential-chaos-shift-keying scheme for chaos-based noncoherent communication[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2012, 59(5): 312–316. doi: 10.1109/TCSII.2012.2190859 KOLUMBAN G and KIS G. Multipath performance of FM-DCSK chaotic communications system[C]. 2000 IEEE International Symposium on Circuits and Systems, Geneva, Switzerland, 2000: 433–436. doi: 10.1109/ISCAS.2000.858781. BAO Jiyu, XU Weikai, WANG Lin, et al. Performance analysis and sub-carriers power allocation for MC-QCSK[C]. 2015 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 2015: 1–5. doi: 10.1109/WCSP.2015.7341173. 张刚, 许嘉平, 张天骐. 基于希尔伯特变换的多用户DCSK通信系统性能分析[J]. 电子与信息学报, 2018, 40(11): 2744–2751. doi: 10.11999/JEIT180110ZHANG Gang, XU Jiaping, and ZHAGN Tianqi. Performance analyze for multiuser-DCSK communication system based on hilbert transform[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2744–2751. doi: 10.11999/JEIT180110 YANG Hua, JIANG Guoping, TANG W K S, et al. Multi-carrier differential chaos shift keying system with subcarriers allocation for noise reduction[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(11): 1733–1777. doi: 10.1109/TCSII.2017.2752754 张刚, 赵畅畅, 张天骐. 短参考正交多用户差分混沌键控方案的性能分析[J]. 电子与信息学报, 2019, 41(9): 2055–2062. doi: 10.11999/JEIT181038ZHANG Gang, ZHAO Changchang, and ZHANG Tianqi. Performance analysis of short reference orthogonal multiuser differential chaotic shift keying scheme[J]. Journal of Electronics &Information Technology, 2019, 41(9): 2055–2062. doi: 10.11999/JEIT181038 TALEB F, BENDIMERAD F T, and ROVIRAS D. Very high efficiency differential chaos shift keying system[J]. IET Communications, 2016, 10(17): 2300–2307. doi: 10.1049/iet-com.2016.0411 KADDOUM G, RICHARDSON F D, and GAGNON F. Design and analysis of a multi-carrier differential chaos shift keying communication system[J]. IEEE Transactions on Communications, 2013, 61(8): 3281–3291. doi: 10.1109/TCOMM.2013.071013.130225 张刚, 郝怡曼, 张天骐. 短参倍速差分混沌键控系统[J]. 系统工程与电子技术, 2018, 40(1): 184–190. doi: 10.3969/j.issn.1001-506X.2018.01.27ZHANG Gang, HAO Yiman, and ZHANG Tianqi. Short reference multifold rate differential chaos shift keying[J]. Systems Engineering and Electronics, 2018, 40(1): 184–190. doi: 10.3969/j.issn.1001-506X.2018.01.27 CAI Guofa, WANG Lin, and CHEN Guanrong. Capacity of the non-coherent DCSK system over Rayleigh fading channel[J]. IET Communications, 2016, 10(18): 2663–2669. doi: 10.1049/iet-com.2016.0487 -





 下载:
下载:











 下载:
下载:
