Certificateless Puklic Key Encryption With Equality Test of Supporting Keyword Search
-
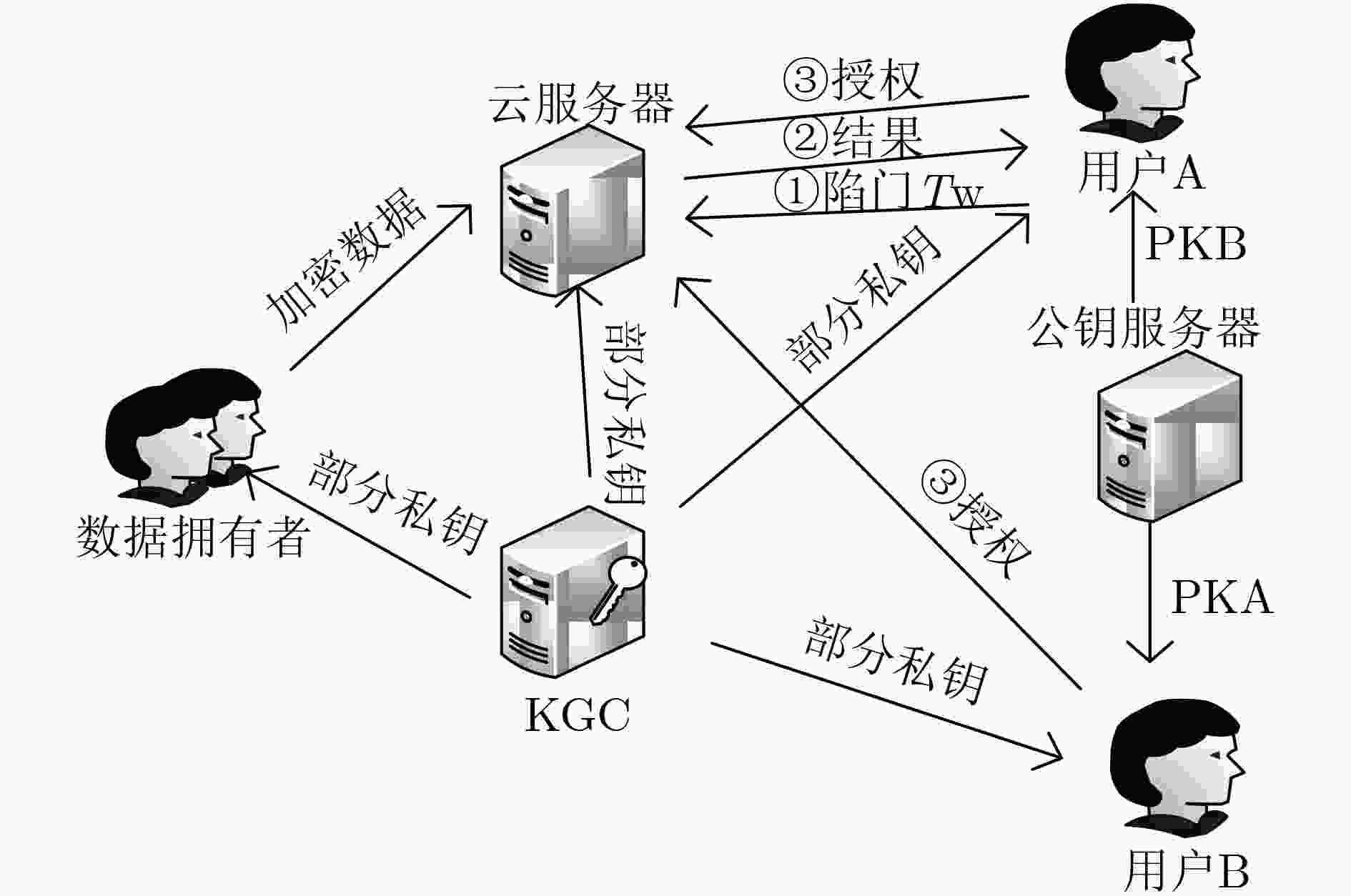
摘要: 公钥加密等值测试(PKEET)可以实现云环境下不同公钥加密数据之间的密文等值比较,即不对密文解密的情况下测试两个密文对应的明文是否一致。但是,密文等值测试加密不提供关键字密文搜索功能。已有密文等值测试加密方案直接以消息生成陷门作为等值测试的凭证,测试的准确度不高,搜索效率较低。针对此问题,该文首先提出了支持关键字搜索的无证书密文等值测试加密(CLEETS)方案。方案通过关键字检索判断是否包含自己需要的信息,根据判断结果选择执行等值测试,从而避免无效测试。然后,在随机预言机模型下证明该方案满足适应性选择关键词不可区分性。最后,对方案进行功能和效率对比。对比结果表明,该文方案的计算代价略高,但是方案在密文等值测试加密中实现了关键字的检索功能,弥补了效率低的不足。Abstract: Public Key Encryption with Equality Test (PKEET) is an important method to achieve the equality test of ciphertexts which are generated by the different public key aiming to the same plaintext in cloud environment. In other words, it can tests the plaintext corresponding to the two ciphertext’s equivalence without decrypting the ciphertext, but does not supply the searchable function. Nowadays, the existing PKEET scheme takes directly the message to generate a trapdoor as the proof of equality test, which has low test accuracy and search efficiency. To solve the above problems, a certificateless public key encryption with equality test scheme supporting keyword search (CertificateLess Equality test EncrypTion with keyword Search, CLEETS) is proposed. The scheme determines whether it contains information needed by the user through the keyword search, then performs the equality test according to the search result, which can avoid invalid test. Then, it is proved that the scheme satisfies the indistinguishability of adaptive selection of keywords under the random oracle model. Finally, the comparison analyses of function and efficiency are performed. The results indicate the computation cost of CLEETS scheme is less efficient. Fortunately, it can realizes the function of keyword search in encryption with equality test, which can remedies the inefficiency.
-
表 1 功能对比
表 2 通信开销
方案 部分私钥长度 秘密值长度 公钥长度 密文长度 文献[6]方案 |2Zq| |2Zq| |2G1| n(|G1|+lgq) 本文方案 |2G1| |2Zq| |2G1| n(|G1|+|G2|+lgq) 表 3 计算代价(ms)
密钥生成 加密 陷门 授权 测试算法1 测试算法2 4Tex +2TH +2Tsm=38.252 4Tex +3Tb +Tmul +2TH +2Tsm=
40.365TH +Tex +Tmul =11.473 Tex =5.611 2Tb +Tex=6.953 4Tb +2TH=14.208 -
张键红, 李鹏燕. 一种有效的云存储数据完整性验证方案[J]. 信息网络安全, 2017(3): 1–5. doi: 10.3969/j.issn.1671-1122.2017.03.001ZHANG Jianhong and LI Pengyan. An efficient data integrity verification scheme for cloud storage[J]. Netinfo Security, 2017(3): 1–5. doi: 10.3969/j.issn.1671-1122.2017.03.001 MAYER-SCHONBERGER V and CUKIER K. Big data: A Revolution that Will Transform How We Live, Work and Think[M]. London: John Murray, 2013: 94–98. SONG D X, WAGNER D, and PERRIG A. Practical techniques for searches on encrypted data[C]. 2000 IEEE Symposium on Security and Privacy, Berkeley, USA, 2000: 44–55. doi: 10.1109/SECPRI.2000.848445. BONEH D, DI CRESCENZO G, OSTROVSKY R, et al. Public key encryption with keyword search[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 506–522. doi: 10.1007/978-3-540-24676-3_30. 江明明, 郭宇燕, 余磊, 等. 有效的标准模型下格上基于身份的代理重加密[J]. 电子与信息学报, 2019, 41(1): 61–66. doi: 10.11999/JEIT180146JIANG Mingming, GUO Yuyan, YU Lei, et al. Efficient identity-based proxy re-encryption on lattice in the standard model[J]. Journal of Electronics &Information Technology, 2019, 41(1): 61–66. doi: 10.11999/JEIT180146 PENG Yanguo, CUI Jiangtao, PENG Changgen, et al. Certificateless public key encryption with keyword search[J]. China Communications, 2014, 11(11): 100–113. doi: 10.1109/CC.2014.7004528 MA Mimi, HE Debiao, KUMAR N, et al. Certificateless searchable public key encryption scheme for industrial internet of things[J]. IEEE Transactions on Industrial Informatics, 2018, 14(2): 759–767. doi: 10.1109/TII.2017.2703922 MA Mimi, HE Debiao, KHAN M K, et al. Certificateless searchable public key encryption scheme for mobile healthcare system[J]. Computers & Electrical Engineering, 2018, 65: 413–424. doi: 10.1016/j.compeleceng.2017.05.014 张玉磊, 刘祥震, 郎晓丽, 等. 云存储环境下多服务器的密钥聚合可搜索加密方案[J]. 电子与信息学报, 2019, 41(3): 674–679. doi: 10.11999/JEIT180418ZHANG Yulei, LIU Xiangzhen, LANG Xiaoli, et al. Multi-server key aggregation searchable encryption scheme in cloud environment[J]. Journal of Electronics &Information Technology, 2019, 41(3): 674–679. doi: 10.11999/JEIT180418 张玉磊, 刘文静, 刘祥震, 等. 基于授权的多服务器可搜索密文策略属性基加密方案[J]. 电子与信息学报, 2019, 41(8): 1808–1814. doi: 10.11999/JEIT180944ZHANG Yulei, LIU Wenjing, LIU Xiangzhen, et al. Searchable multi-server CP-ABE scheme based on authorization[J]. Journal of Electronics &Information Technology, 2019, 41(8): 1808–1814. doi: 10.11999/JEIT180944 YANG Guomin, TAN C H, HUANG Qiong, et al. Probabilistic public key encryption with equality test[C]. Cryptographers’ Track at the RSA Conference 2010, San Francisco, USA, 2010: 119–131. doi: 10.1007/978-3-642-11925-5_9. TANG Qiang. Towards public key encryption scheme supporting equality test with fine-grained authorization[C]. The 16th Australasian Conference on Information Security and Privacy, Melbourne, Australia, 2011: 389–406. TANG Qiang. Public key encryption supporting plaintext equality test and user-specified authorization[J]. Security and Communication Networks, 2012, 5(12): 1351–1362. doi: 10.1002/sec.418 TANG Qiang. Public key encryption schemes supporting equality test with authorisation of different granularity[J]. International Journal of Applied Cryptography, 2012, 2(4): 304–321. doi: 10.1504/IJACT.2012.048079 MA Sha, HUANG Qiong, ZHANG Mingwu, et al. Efficient public key encryption with equality test supporting flexible authorization[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(3): 458–470. doi: 10.1109/TIFS.2014.2378592 MA Sha. Identity-based encryption with outsourced equality test in cloud computing[J]. Information Sciences, 2016, 328: 389–402. doi: 10.1016/j.ins.2015.08.053 QU Haipeng, YAN Zhen, LIN Xijun, et al. Certificateless public key encryption with equality test[J]. Information Sciences, 2018, 462: 76–92. doi: 10.1016/j.ins.2018.06.025 HUANG Kaibin, TSO R, CHEN Yuchi, et al. PKE-AET: Public key encryption with authorized equality test[J]. The Computer Journal, 2015, 58(10): 2686–2697. doi: 10.1093/comjnl/bxv025 LEE H T, LING San, SEO J H, et al. Semi-generic construction of public key encryption and identity-based encryption with equality test[J]. Information Sciences, 2016, 373: 419–440. doi: 10.1016/j.ins.2016.09.013 The pairing-based cryptography library[EB/OL]. http://crypto.stanford.edu/pbc/, 2015. -





 下载:
下载:


 下载:
下载:
