Application of Finite Element-Based Domain Decomposition Method to the Simulation for Permanent Magnet Focusing System
-
摘要:
随着计算机技术以及并行求解技术的发展,区域分解方法越来越多地应用于计算电磁学的各个领域。针对微波管中的永磁聚焦系统仿真,该文提出一种基于有限元的非重叠区域分解方法,其引入一种新型传输条件,并采用内罚的方式推导出有限元弱形式。该区域分解法的最大优势是不需要引入多余的未知量,并且最终集成的有限元矩阵满足对称正定性,适合采用预处理共轭梯度法进行矩阵方程的求解。该文仿真了多个微波管永磁聚焦系统,并与商业软件Maxwell进行了详细的对比,结果表明所提出的区域分解方法和Maxwell精度相当,却拥有着更加优越的计算性能。
Abstract:With the development of computer technology and parallel solving technology, domain decomposition method has been increasingly applied to various fields of computational electromagnetics. For the simulation of microwave tube permanent magnet focusing system, this paper proposes a finite element-based non-overlapping domain decomposition method, and introduces a novel transmission condition. Then the interior penalty formulation is used to derive the finite element weak form. The biggest advantage of the proposed domain decomposition method is that no extra unknowns are introduced, and the final finite element matrix is symmetric and positive definite, which makes the matrix equation suitable be solved by the preconditioned conjugate gradient method. In this paper, several microwave tube permanent magnet focusing systems are simulated and compared with the commercial software Maxwell in detail. The results show that the proposed domain decomposition method has the same accuracy as Maxwell, but has a more superior computational performance.
-
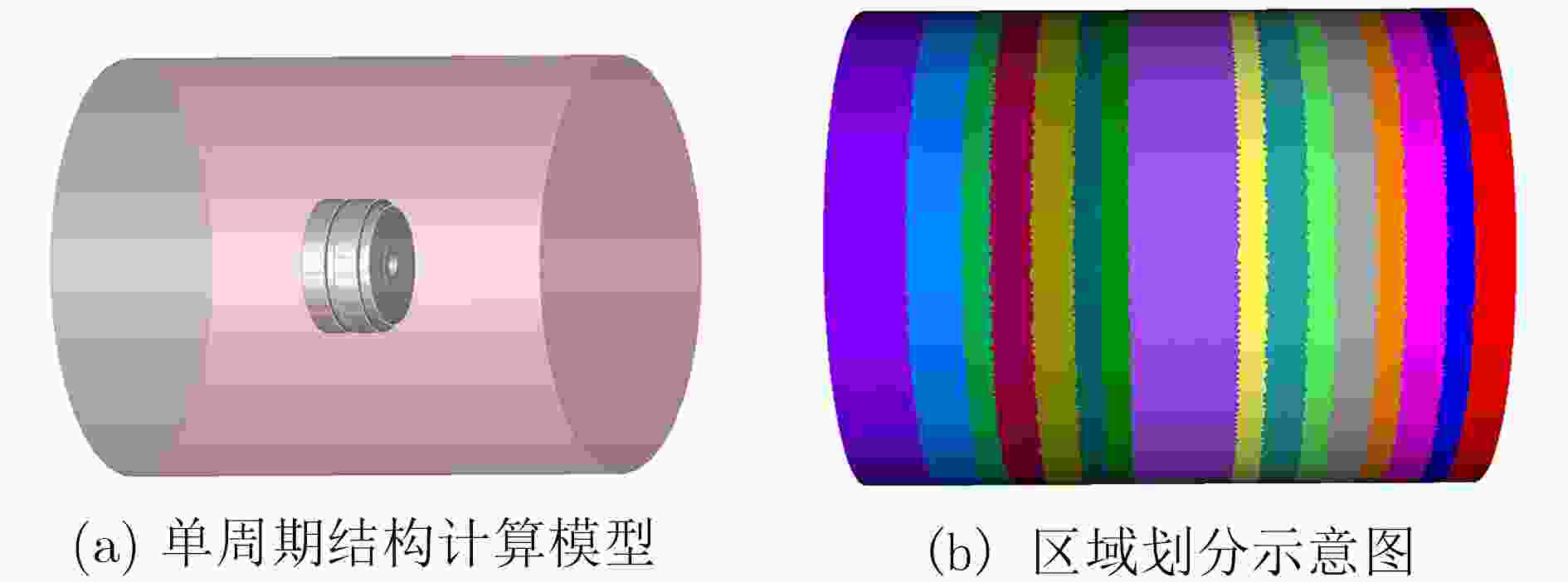
表 1 单周期结构区域分解法与Maxwell软件性能对比
求解方法 子区域数 网格数 计算时间(s) 峰值内存(MB) Maxwell 2428919 435 10342 区域分解法 8 2718101 291 8129 12 2718101 135 7111 16 2718101 132 6461 20 2718101 38 5532 表 2 Wiggler结构区域分解法与Maxwell性能对比
实例 网格数 求解方法 计算时间(s) 峰值内存(MB) 实例1 5987880 Maxwell 2171 30515 6476933 区域分解法 589 23407 实例2 7784252 Maxwell 2717 35942 8200780 区域分解法 858 29387 实例3 9014971 Maxwell 4766 45875 9158627 区域分解法 1129 33466 -
PARKER R K, ABRAMS R H, DANLY B G, et al. Vacuum electronics[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(3): 835–845. doi: 10.1109/22.989967 SRIKRISHNA P, CHANAKYA T, VENKATESWARAN R, et al. Thermal analysis of high-average power helix traveling-wave tube[J]. IEEE Transactions on Electron Devices, 2018, 65(6): 2218–2226. doi: 10.1109/TED.2017.2786941 LIU Gaofeng, XUE Qianzhong, ZHANG Shan, et al. Development and demonstration of a Ka-band gyrotron traveling-wave tube[J]. IEEE Transactions on Plasma Science, 2018, 46(6): 1975–1983. doi: 10.1109/TPS.2018.2835843 CHEN Wenlong, HU Quan, HU Yulu, et al. Magnetic focusing simulator: A 3-D finite-element permanent-magnet focusing system design tool[J]. IEEE Transactions on Electron Devices, 2015, 62(4): 1319–1326. doi: 10.1109/TED.2015.2400993 YANG Wenying, PENG Fei, DINAVAHI V, et al. A generalized parallel transmission line iteration for finite element analysis of permanent magnet axisymmetrical actuator[J]. IEEE Transactions on Magnetics, 2019, 55(3): 7400410. doi: 10.1109/TMAG.2018.2885966 FU Dongshan, XU Yanliang, GILLON F, et al. Presentation of a novel transverse-flux permanent magnet linear motor and its magnetic field analysis based on Schwarz-Christoffel mapping method[J]. IEEE Transactions on Magnetics, 2018, 54(3): 6000204. doi: 10.1109/TMAG.2017.2756847 ANSYS. Maxwell 3D electromagnetic field solver[EB/OL]. https://www.ansys.com/products/electronics/ansys-maxwell, 2019. LI Bin, YANG Zhonghai, LI Jianqing, et al. Theory and design of microwave-tube simulator suite[J]. IEEE Transactions on Electron Devices, 2009, 56(5): 919–927. doi: 10.1109/TED.2009.2015413 LU Jiaqing, CHEN Yongpin, LI Dongwei, et al. An embedded domain decomposition method for electromagnetic modeling and design[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(1): 309–323. doi: 10.1109/TAP.2018.2874751 BELGACEM F B. The mortar finite element method with Lagrange multipliers[J]. Numerische Mathematik, 1999, 84(2): 173–197. doi: 10.1007/s002110050468 KÖPPEL M, MARTIN V, and ROBERTS J E. A stabilized Lagrange multiplier finite-element method for flow in porous media with fractures[J]. GEM-International Journal on Geomathematics, 2019, 10(1): 7. doi: 10.1007/s13137-019-0117-7 SHAO Yang, PENG Zhen, and LEE J F. Thermal-aware DC IR-drop co-analysis using non-conformal domain decomposition methods[J]. Proceedings of the Royal Society A, 2012, 468(2142): 1652–1675. doi: 10.1098/rspa.2011.0708 RAWAT V. Finite element domain decomposition with second order transmission conditions for time-harmonic electromagnetic problems[D]. [Ph. D. dissertation], The Ohio State University, 2009: 11–19. MATSUO T, OHTSUKI Y, and SHIMASAKI M. Efficient linear solvers for mortar finite-element method[J]. IEEE Transactions on Magnetics, 2007, 43(4): 1469–1472. doi: 10.1109/TMAG.2007.891415 LIONS P L. On the Schwarz alternating method III: A variant for nonoverlapping subdomains[C]. The 3rd International Symposium on Domain Decomposition Methods for Partial Differential Equations. Philadelphia, USA, 1990: 202–223. BLANDFORD G E and TAUCHERT T R. Thermoelastic analysis of layered structures with imperfect layer contact[J]. Computers & Structures, 1985, 21(6): 1283–1291. doi: 10.1016/0045-7949(85)90182-8 SAVIJA I, CULHAM J R, YOVANOVICH M M, et al. Review of thermal conductance models for joints incorporating enhancement materials[J]. Journal of Thermophysics and Heat Transfer, 2003, 17(1): 43–52. doi: 10.2514/2.6732 WEBB J P and FORGAHANI B. Hierarchal scalar and vector tetrahedra[J]. IEEE Transactions on Magnetics, 1993, 29(2): 1495–1498. doi: 10.1109/20.250686 YIN Junhui, XU Li, WANG Hao, et al. Accurate and fast three-dimensional free vibration analysis of large complex structures using the finite element method[J]. Computers & Structures, 2019, 221: 142–156. doi: 10.1016/j.compstruc.2019.06.002 KARYPIS G. A software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices[EB/OL]. http://glaros.dtc.umn.edu/gkhome/fetch/sw/metis/manual.pdf, 2013. -





 下载:
下载:



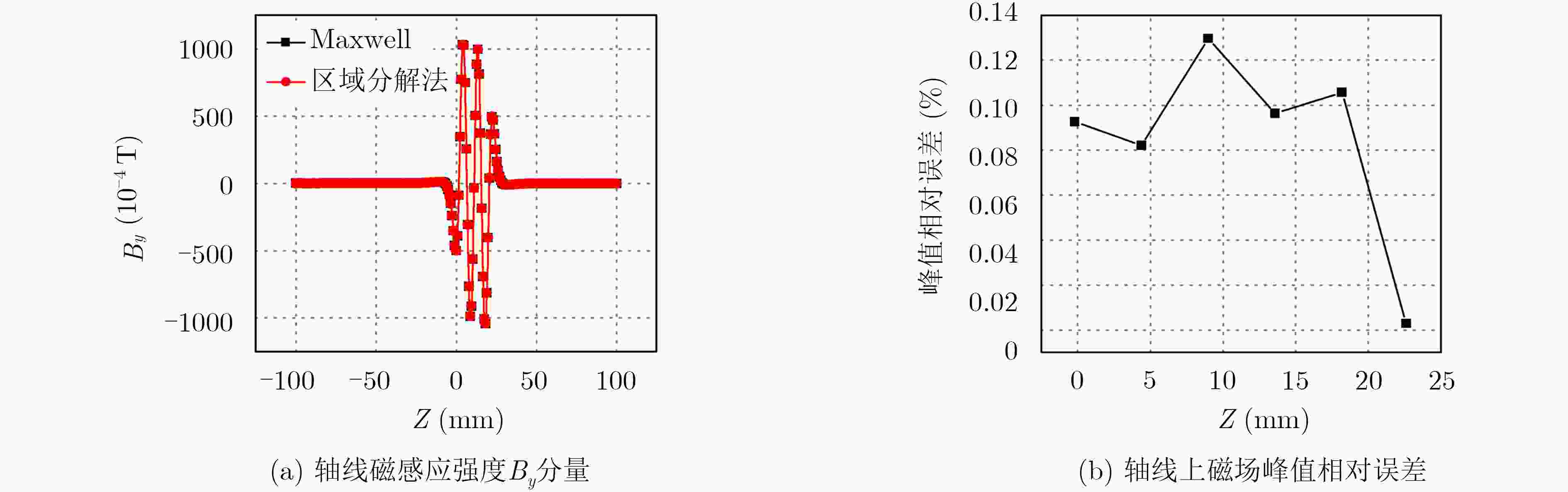


 下载:
下载:
