基于深度神经网络的Morse码自动译码算法

游凌; 李伟浩; 张文林; 王科人

doi:10.11999/JEIT190658

基于深度神经网络的Morse码自动译码算法

doi: 10.11999/JEIT190658

游凌²,
李伟浩^{1, 2, ,},
张文林¹,
王科人²

1.
战略支援部队信息工程大学郑州 450001
2.
盲信号处理国家级重点实验室成都 610041

基金项目: 国家自然科学基金(61403415)，中国博士后科学基金(2016M602975)

详细信息

作者简介:
游凌：男，1971年生，博士，研究员，研究方向为信号分析

李伟浩：男，1996年生，硕士生，研究方向为深度学习、信号分析

张文林：男，1982年生，博士，副教授，研究方向为语音信号处理、语音识别、自然语言理解

王科人：男，1986年生，博士，助理研究员，研究方向为信号分析、智能信息处理

通讯作者:
李伟浩　liweihao315@gmail.com

中图分类号: TN919.32
计量
- 文章访问数: 3997
- HTML全文浏览量: 1186
- PDF下载量: 178
- 被引次数: 0
出版历程
- 收稿日期: 2019-08-29
- 修回日期: 2020-05-08
- 网络出版日期: 2020-05-28
- 刊出日期: 2020-11-16

Automatic Decoding Algorithm of Morse Code Based on Deep Neural Network

Ling YOU²,
Weihao LI^{1, 2
, ,},
Wenlin ZHANG¹,
Keren WANG²

1.
PLA Strategic Support Force Information Engineering University, Zhengzhou 450001, China
2.
National Key Laboratory of Science and Technology on Blind Signal Processing, Chengdu 610041, China

Funds: The National Natural Science Foundation of China (61403415), The Postdoctoral Science Foundation of China(2016M602975)

摘要

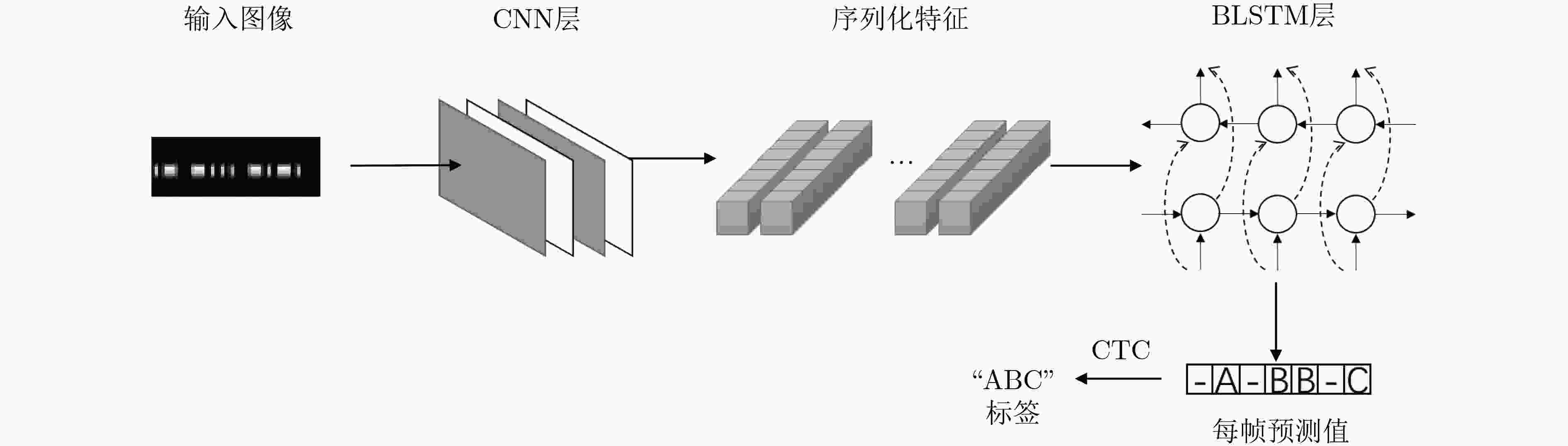
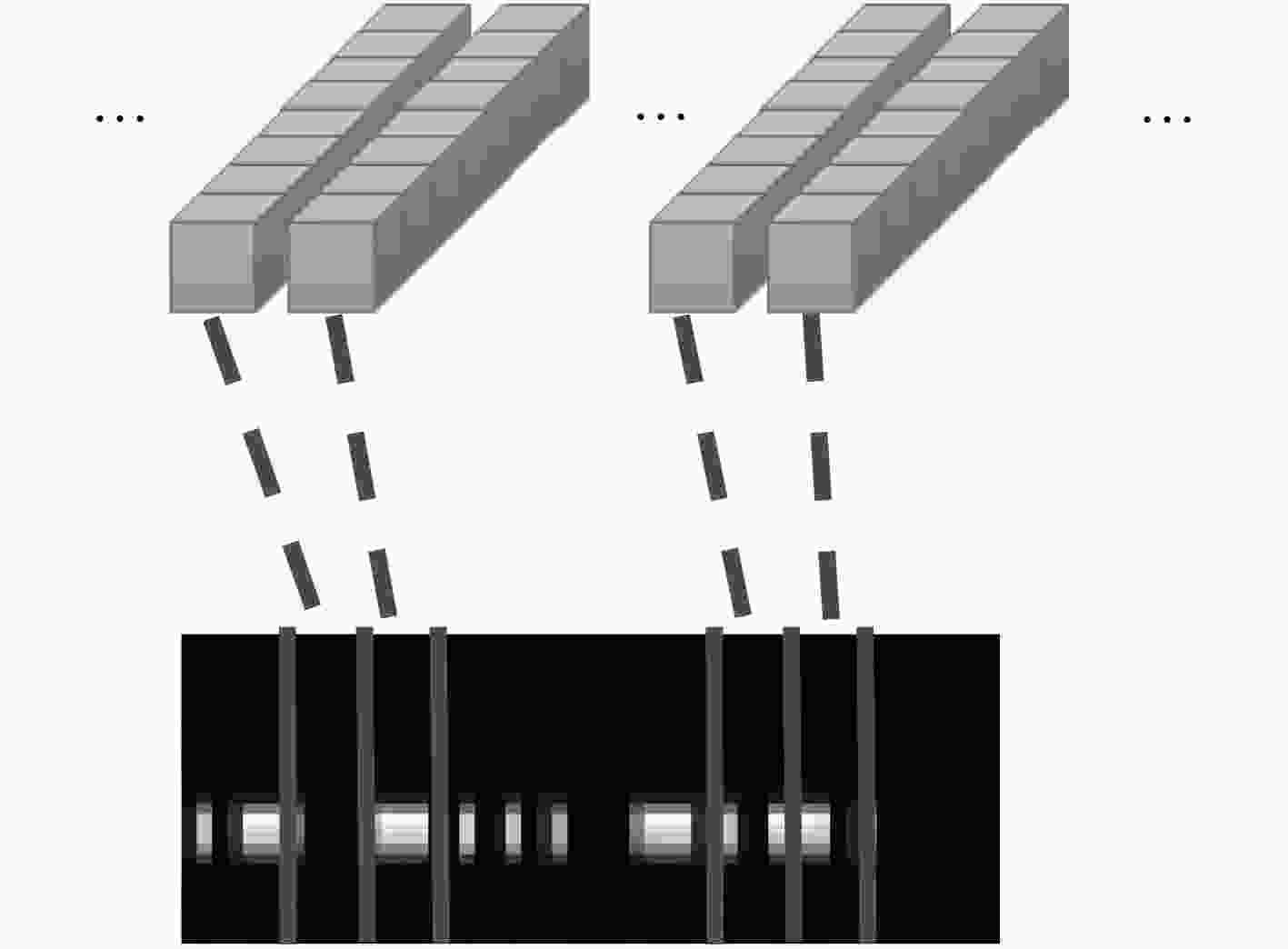
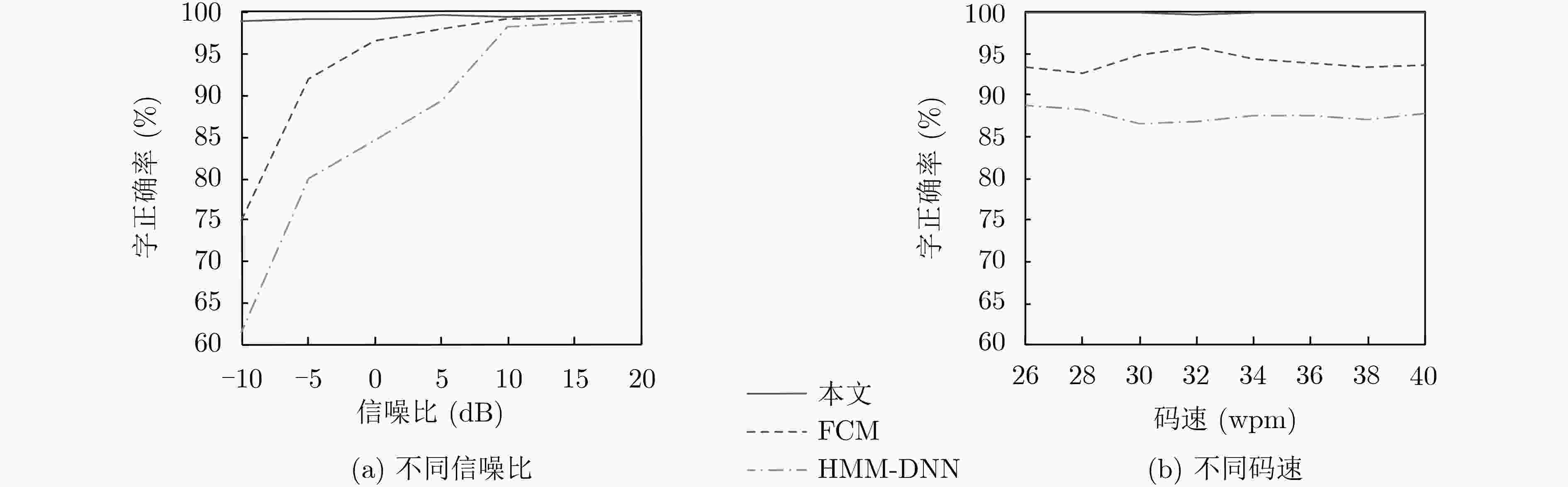
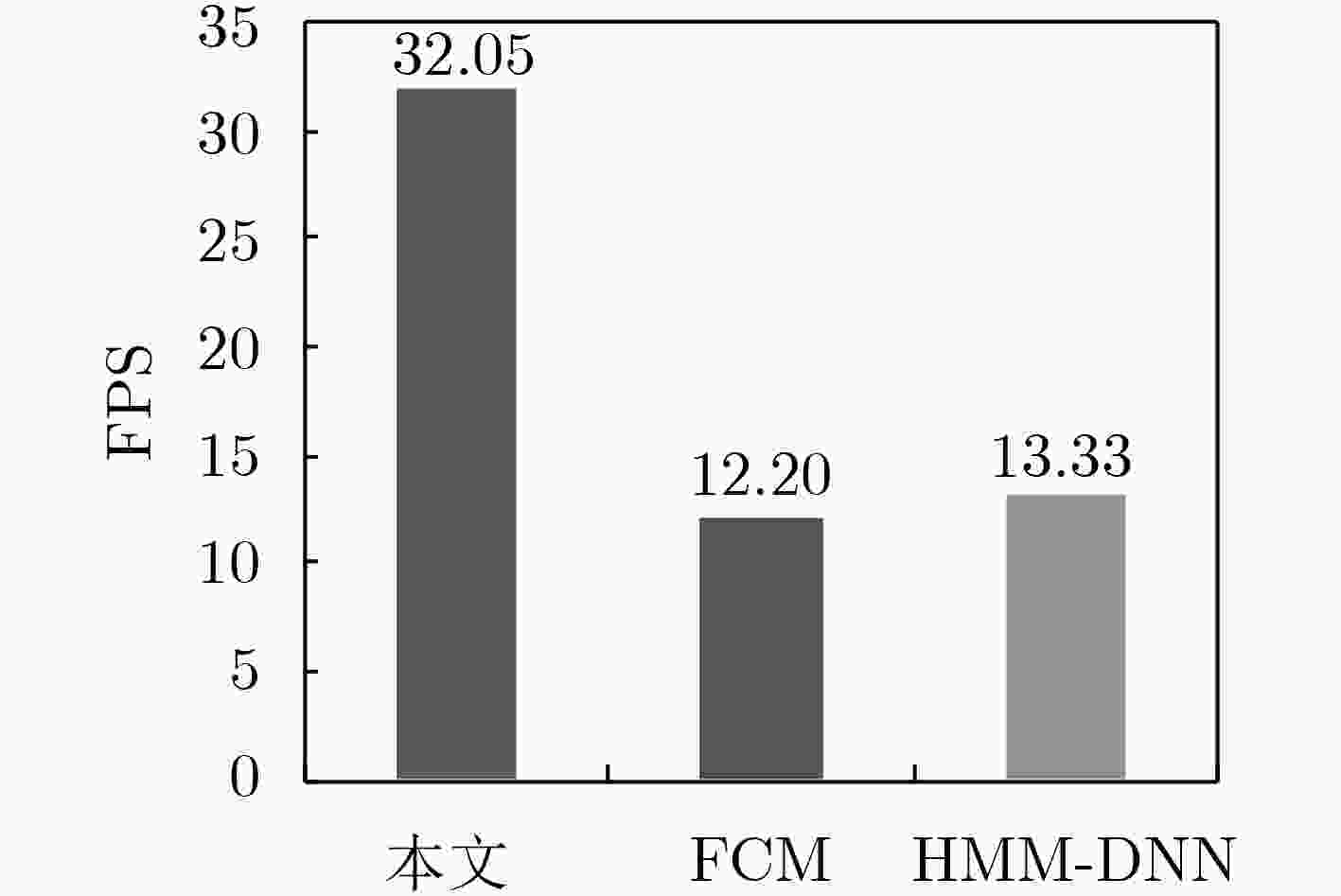
摘要: 在军用和民用领域，Morse电报一直是一种重要的短波通信手段，但目前的自动译码算法仍然存在准确率低、无法适应低信噪比和不稳定的信号等问题。该文引入深度学习方法构建了一个Morse码自动识别系统，神经网络模型由卷积神经网络、双向长短时记忆网络和连接时序分类层组成，结构简单，且能够实现端到端的训练。相关实验表明，该译码系统在不同信噪比、不同码速、信号出现频率漂移以及不同发报手法引起的码长偏差等情况下，均能取得较好的识别效果，性能优于传统的自动识别算法。
- Morse码 /
- 自动译码 /
- 深度学习 /
- 频率漂移 /
- 码长偏差
Abstract: In the military and civilian fields, the Morse telegraph is always as an important means of short-wave communication, but the current automatic decoding algorithms still have problems such as low accuracy, inability to adapt to low signal-to-noise ratio and unstable signals. A deep learning method is introduced to construct a Morse code automatic recognition system. The neural network model consists of convolutional neural network, bidirectional long short-term memory network and connectionist temporal classification layer. The structure is simple and can implement end-to-end training. Related experiments show that the decoding system can achieve good recognition results under different signal-to-noise ratio, code rate, frequency drift and code length deviation caused by different sending manipulation, and the performance is better than the traditional recognition algorithms.
- Morse code /
- Automatic decoding /
- Deep learning /
- Frequency drift /
- Code length deviation

HTML全文

1. 引言

随着人类太空探索及航天活动的不断增加，轨道中包含着大量空间碎片及失效卫星等微动目标。同时，中段或再入段弹道目标(如舱体、诱饵、弹头等)也具有自旋、进动等典型微动。因此，如何从空间微动目标独特的微多普勒调制中提取丰富的形状、结构和运动信息，进而实现有效的分类识别在空间态势感知及弹道目标防御中具有重要作用^[1-3]。

针对微动目标窄带回波，主要提取均值、方差、中位数、极值、标准差等统计特征和微动周期等运动特征^[4]。针对窄带回波时频图(Joint Time-Frequency, JTF)^[5]，主要提取周期、多普勒调制带宽等物理特征和图像熵、矩、方向性、倒谱、双相关系数等统计特征^[6]。在此基础上，可对JTF沿时间轴做傅里叶变换得到2维韵律频谱(Cadence Velocity Diagram, CVD)，并从CVD及平均归一化CVD序列中提取伪泽尼克矩等相关统计特征^[7]。针对微动目标宽带回波，可从高分辨1维距离像(High Resolution Range Profiles, HRRP)序列中估计微动频率及尺寸^[8]。同时，通过在距离-慢时间域进行逆Radon变换提取目标运动及散射点分布特征^[9]。

综上所述，现有空间微动目标识别方法主要为物理驱动，即根据专家经验及先验知识设计特征提取器(如区域特征、轮廓特征、散射特征、运动特征等)和分类器，该过程耗时较长且难以推广。同时，大部分微动目标识别方法要求目标的观测时间应大于一个微动周期，由于多功能雷达任务繁多、资源有限，很难满足该要求。此外，空间微动目标观测时往往能够同时获得其宽、窄带回波，而现有识别方法仅从宽带或窄带等单一回波中提取特征。由于难以充分利用空、时、频信息，因此识别精度较低。当目标特性或雷达参数变化时，对单一回波的高度依赖会造成识别方法性能下降甚至完全失效。

针对上述空间微动目标识别中的难点与关键问题，本文提出基于稀疏自编码器(Sparse Auto-Encoder, SAE)的空间微动目标特征级融合识别方法。该方法为数据驱动，能够自动提取有助于识别的目标特征，从而避免了人工特征设计及选择环节，具有较强的泛化能力^[10]。在训练阶段，首先采用卷积神经网络(Convolution Neural Network, CNN)分别提取HRRP, JTF、距离-瞬时多普勒(Range Instantaneous Doppler, RID)像的层级特征，进而通过特征拼接形成联合特征向量。随后，采用SAE无监督地学习出联合特征向量的隐层特征。进而剔除SAE解码器部分并在编码器后接入Softmax分类器构成识别网络。最后利用SAE网络参数对识别网络进行初始化，并利用上述联合特征向量对其进行微调得到训练好的识别网络。在测试阶段，将CNN所提测试集的联合特征向量直接输入训练好的识别网络中，得到融合识别结果。各种条件下的电磁仿真数据识别结果表明，即使观测时间小于目标微动周期，所提方法仍然能够获得优良的识别性能。同时，与仅采用单一回波的识别方法相比，所提方法显著提升了识别正确率，并且对噪声具有稳健性。

2. 建模

2.1 微动建模

空间微动目标通常包含自旋、进动、章动、旋转、翻滚等多种微动形式。在目标本地坐标系中，若初始时刻散射中心 $p$ 的坐标矢量为 ${{\boldsymbol{r}}_p} = {[{x_p},{y_p},{z_p}]^{\rm{T}}}$ ，雷达视线矢量为 $\xi$ ，则该散射点瞬时斜距满足

${R_p}\left( t \right) = \left\langle {{{\boldsymbol{R}}_{{\rm{rot}}}}{{\boldsymbol{r}}_p},\xi } \right\rangle$

(1)

其中， $\left\langle {} \right\rangle$ 表示内积， ${{\boldsymbol{R}}_{{\rm{rot}}}}$ 为旋转矩阵，具体表达式由目标微动形式决定^[2]。

2.2 信号建模

在距离脉压后，微动目标回波满足

$\begin{split} g\left( {r,t} \right) = &\sum\nolimits_p {{\sigma _p}a\left( {\frac{{2B}}{{\rm{c}}}\left( {r - \Delta {R_p}\left( t \right)} \right)} \right)}\\ & \cdot{\text{exp}}\left( { - {\rm{j}}\frac{{4\pi }}{\lambda }\Delta {R_p}\left( t \right)} \right) \end{split}$

(2)

其中， $p$ 表示散射点序号， ${\sigma _p}$ 表示第 $p$ 个散射点的后向散射系数， $a(\cdot)$ 为与波形相关的函数， $B$ 为信号带宽， ${\rm{c}}$ 为光速， $\Delta {R_p}\left( t \right){\text{ = }}{R_p}\left( t \right) - {R_{{\rm{ref}}}}$ ， ${R_{{\rm{ref}}}}$ 为参考距离， $\lambda {\text{ = }}{\rm{c}}/{f_c}$ 为载频对应的波长。

对于窄带雷达，目标回波集中在一个距离单元内，因此式(2)退化为

${g_n}\left( {r,t} \right) = \sum\nolimits_p {{\sigma _p}} {\text{exp}}\left( { - {\rm{j}}\frac{{4\pi }}{\lambda }\Delta {R_p}\left( t \right)} \right)$

(3)

2.3 预处理

在获得目标原始回波后，对其对做短时傅里叶变换(Short-Time Fourier Transform, STFT)得到联合时频分布图。对于窄带回波 ${g_n}\left( {r,t} \right)$ ，

${\rm{STFT}}\left( {t,\omega } \right) = \int {{g_n}\left( {r,t'} \right)h\left( {t - t'} \right)\exp \left\{ { - {\rm{j}}\omega t'} \right\}{\rm{d}}t'}$

(4)

其中， $t$ 和 $\omega$ 分别是时间与多普勒单元， $h(\cdot)$ 是窗函数。

对于宽带回波，可进一步进行距离-瞬时多普勒成像^[11]。设宽带回波分别包含 ${N_r}$ 个距离单元和 ${N_a}$ 个方位单元，则在距离脉压后对 ${N_r}$ 个距离单元分别作短时傅里叶变换得到其时频图 ${I_n}\left( {{t_m},{f_d}} \right) \in {\mathbb{R}^{M \times {N_d}}}$ ，其中 $n = 1,2, \cdots ,{N_r}$ , $M = \left\lfloor {\left( {{N_a} - L/2} \right)/{s_{{\rm{tr}}}}} \right\rfloor$ , $m = 1,2, \cdots ,M$ , $L$ 为窗长， ${s_{{\rm{tr}}}}$ 为步长， ${N_d}$ 是多普勒单元的数量。然后，将时频图 ${I_n}\left( {{t_m},{f_d}} \right)$ 堆叠成一个3维矩阵 ${\boldsymbol{Q}}\left( {n,{t_m},{f_d}} \right) \in {\mathbb{R}^{{N_r} \times M \times {N_d}}}$ 并沿时间轴抽取2维矩阵切片，即可得RID像。

3. 所提算法

本节将详细介绍基于SAE的空间微动目标特征级融合识别方法，该方法的流程如图1所示。在训练阶段，首先采用CNN分别提取HRRP, JTF, RID像的层级特征，进而通过特征拼接形成联合特征向量。随后，采用SAE无监督地学习出联合特征向量的隐层特征。进而剔除SAE解码器部分并在编码器后接入Softmax分类器构成识别网络。最后利用SAE网络参数对识别网络进行初始化，并利用上述联合特征向量对其进行微调得到训练好的识别网络。在测试阶段，将CNN所提测试集的联合特征向量直接输入训练好的识别网络中，得到融合识别结果，下面将详细介绍各模块结构。

图 1 基于SAE的空间微动目标特征级融合识别流程

下载: 全尺寸图片幻灯片

3.1 基于CNN的特征提取

与基于手动特征提取的传统目标识别方法不同，CNN的数据驱动机制能够避免复杂的特征提取器设计。此外，其局部连接、权值共享、池化及多层结构^[10]保证了层级特征的有效提取。对于从微动目标宽带回波获得的HRRP序列、RID像及从窄带回波获得的JTF，本文分别设计3种CNN结构用于数据域特征提取，如所示。以为例，CNN-I网络“Conv.16@5×5 BN/ReLU/Dropout”表示卷积层中特征图数量为16，卷积核大小为 $5 \times 5$ ，卷积核滑动步长为1，在每个卷积层之后加入批归一化BN^[12]和整流线性单元(ReLU)^[13]进行激活，为防止过拟合在该层之后加入dropout层^[14]；“Max pool 2×2”表示采用最大池化，池化核大小为 $2 \times 2$ ，滑动步长为2；“Fully connected/256”表示全连接层，全连接点数为256。同时，CNN-I网络结构共包含4个卷积层、4个池化层和2个全连接层。4个卷积层的卷积核大小分别为 $5 \times 5$ , $5 \times 5$ , $4 \times 4$ 和 $4 \times 4$ ，步长均为1；对应卷积特征图数量分别为16, 32, 64, 128。第1个全连接层节点数为256，第2个全连接层节点数为4。最后，通过Softmax分类器输出预测标签。为进一步防止过拟合，在CNN-I和CNN-III中将网络部分权重以0.1概率随机剔除，CNN-II中网络部分权重以0.2概率随机剔除。

图 2 CNN网络结构

下载: 全尺寸图片幻灯片

在训练过程中，输出层损失函数采用交叉熵损失函数

$L\left( {\boldsymbol{w}} \right) = - \sum\limits_{t = 1}^T {{y_t}\ln {{\hat y}_t}} \left( {\boldsymbol{w}} \right)$

(5)

其中， ${\hat y_t}$ 为激活函数Softmax的输出， ${y_t}$ 为样本标签， $T$ 为总的目标类别数， ${\boldsymbol{w}}$ 为网络参数。

所提方法中，将第1个全连接层输出作为提取的深层特征。因此对于HRRP序列，JTF及RID像，可分别提取一个256维、128维以及256维的特征向量，进而将其拼接为一个640维的联合特征向量。

3.2 基于SAE的融合识别

在得到联合特征向量后，本文进一步设计SAE以无监督地学习联合特征向量的隐层特征并实现宽、窄带特征融合。相较于传统自编码器，SAE通过引入稀疏惩罚项提升隐层特征的表征能力并减小过拟合风险，同时可以实现特征优选和冗余抑制^[15,16]。如图1所示，本文所设计的SAE包含3层网络结构，即输入层、隐藏层和输出层。

SAE的训练过程包含编码和解码两个阶段。在编码阶段，通过激活函数 $f$ 将联合特征向量 ${\boldsymbol{x}} = \left[ {x^{\left( 1 \right)}}, {x^{\left( 2 \right)}}, \cdots ,{x^{\left( m \right)}} \right]$ 映射到隐藏层 $h$

$h\left( {{x^{\left( i \right)}},{{\boldsymbol{w}}^{\left( 1 \right)}},b} \right) = f\left( {{{\boldsymbol{w}}^{\left( 1 \right)}}{x^{\left( i \right)}} + {b^{\left( 1 \right)}}} \right),{\text{ }}i = 1,2, \cdots ,m$

(6)

其中， ${{\boldsymbol{w}}^{\left( 1 \right)}}$ 为输入层与隐藏层之间的权值矩阵， ${b^{\left( {1} \right)}}$ 为偏置， $m = 640$ 为联合特征向量的长度。在解码阶段，通过激活函数 $g$ 将隐藏层 $h$ 映射到输出层，得到重构联合特征向量 $\hat {\boldsymbol{x}}$ ，其第 $i$ 个元素为

${\hat x^{\left( i \right)}} = g\left( {{{\boldsymbol{w}}^{\left( 2 \right)}}h\left( {{x^{\left( i \right)}},{{\boldsymbol{w}}^{\left( 1 \right)}},b} \right) + {b^{\left( 2 \right)}}} \right),{\text{ }}i = 1,2, \cdots ,m$

(7)

其中， ${{\boldsymbol{w}}^{\left( 2 \right)}}$ 为隐藏层与输出层之间的权值矩阵， ${b^{\left( 2 \right)}}$ 为对应偏置。

传统自编码器通过最小化重构误差训练网络，其代价函数为

$\begin{split} J\left( {{\boldsymbol{w}},b} \right) = & \left[ {\frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{1}{2}{{\left\| {{x^{\left( i \right)}} - {{\hat x}^{\left( i \right)}}} \right\|}^2}} \right)} } \right] \\ & + \frac{\beta }{2}\sum\limits_{l = 1}^{{n_l} - 1} {\sum\limits_{i = 1}^{{s_l}} {\sum\limits_{j = 1}^{{s_{l + 1}}} {{{\left( {{\boldsymbol{w}}_{ji}^{\left( l \right)}} \right)}^2}} } } \end{split}$

(8)

其中，第1项为原始输入 $x$ 与重构输入 $\hat x$ 的均方误差，第2项为权值衰减项，用于防止网络过拟合。 ${n_l}$ 为神经网络的层数， ${s_l}$ 为第 $l$ 层的神经元节点数， $\beta$ 为权值衰减系数。

在传统自编码器的基础上，SAE通过引入稀疏惩罚项 ${P_{{{\rm{penalty}}}}}$ 将隐藏层的神经元节点限制在“不活跃”状态(神经单元节点的激活值为0或者接近于0)，即

$\begin{split} {P_{{\rm{penalty}}}} = & \sum\limits_{j = 1}^{{s_2}} {{\rm{KL}}\left( {\rho \left\| {{{\hat \rho }_j}} \right.} \right)} = \sum\limits_{j = 1}^{{s_2}} {\rho \lg \frac{\rho }{{{{\hat \rho }_j}}}} + \left( {1 - \rho } \right)\\ & \cdot\lg \frac{{\left( {1 - \rho } \right)}}{{\left( {1 - {{\hat \rho }_j}} \right)}} \end{split}$

(9)

${\hat \rho _j} = \frac{1}{m}\sum\limits_{i = 1}^m {{h_j}\left( {{x^{\left( i \right)}},{{\boldsymbol{w}}^{\left( 1 \right)}},b} \right)}$

(10)

其中， $\rho$ 为稀疏参数， ${\hat \rho _j}$ 为隐藏层第 $j$ 个神经元节点的平均激活值， ${h_j}\left( {{x^{\left( i \right)}},{{\boldsymbol{w}}^{\left( 1 \right)}},b} \right)$ 为联合特征向量中第 $i$ 个元素对应的第 $j$ 个隐藏节点的激活值， ${s_2}$ 为隐藏层节点数， ${\rm{KL}}(\cdot)$ 表示KL散度，用于衡量 $\rho$ 与 $\hat \rho$ 分布之间的相似性。SAE的代价函数由重构均方误差式(8)和稀疏惩罚项两项组成

${J_{{\rm{sparse}}}}\left( {{\boldsymbol{w}},b} \right) = J\left( {{\boldsymbol{w}},b} \right) + \gamma \sum\limits_{j = 1}^{{s_2}} {{\rm{KL}}\left( {\rho \left\| {{{\hat \rho }_j}} \right.} \right)}$

(11)

其中， $\gamma$ 为稀疏惩罚系数，用于控制稀疏惩罚项的权重。

本文所设计的SAE输入层和输出层均包含640个节点，隐藏层包含1 024个节点。设置稀疏参数 $\rho {\text{ = }}0.05$ ，稀疏惩罚系数 $\gamma {\text{ = }}0.2$ 。

在采用SAE学习到联合特征向量的隐层特征后，剔除SAE解码器部分，同时在编码器后接入Softmax分类器构成识别网络。而后，利用SAE网络参数对识别网络的参数进行初始化，进而利用联合特征向量对其进行微调得到训练好的识别网络。在测试阶段，用训练好的CNN提取测试样本的联合特征向量并输入识别网络中得到目标类别标签。

4. 实验设置

4.1 数据集设置

由于很难获得空间微动目标的实测数据^[17]，因此本文通过动态电磁仿真获得各类典型微动目标的回波，并通过不同条件下的实验对比分析，验证所提方法的有效性和稳健性。

根据现有空间微动目标识别文献，选取4类典型空间微动目标，同时根据文献给出的参数范围设计了对应目标的尺寸及微动参数^[4,7,17,18]。文中采用的4类目标3维几何模型及剖面图如图3所示，其形状相似、材质相同，分别为平底锥(目标1)、平底锥柱体(目标2)、球底锥(目标3)、球底锥柱体(目标4)。为实现动态回波仿真，首先采用物理光学法^[19]获得目标的静态全角域回波。由于目标旋转对称，因此在本地坐标系中雷达视线方位角固定而俯仰角在0°～360°变化(间隔为0.1°)。雷达工作于X波段，HH极化，载频为10 GHz，宽带信号带宽为2 GHz，窄带信号带宽为20 MHz。图4为4类目标窄带静态全角域回波随俯仰角的变化曲线，图5为4类目标宽带静态全角域回波随俯仰角的变化的曲线。

图 3 4类目标3维模型及剖面图

下载: 全尺寸图片幻灯片

图 4 4类目标RCS值随俯仰角变换关系图

下载: 全尺寸图片幻灯片

图 5 4类目标全俯仰角HRRP成像结果

下载: 全尺寸图片幻灯片

在动态回波仿真时，宽带信号和窄带信号的重频均为200 Hz，观测时间均为0.5 s，4类目标微动参数如所示。各类目标初始俯仰角在21°～30°内以1°为间隔连续变化，进动频率以0.2 Hz为间隔连续变化，进动角以0.15°为间隔连续变化。因此，每类目标对应10个初始俯仰角，11种进动频率(按照设定的观测时间，当进动频率低于2 Hz时，均观测不到一个完整周期)，11个进动角。为获得目标动态电磁仿真回波，首先根据微动参数计算出雷达视线与目标对称轴的夹角(等效俯仰角)，进而分别对窄带和宽带全角域静态电磁回波进行抽取^[20]。最终，每类目标可得到1 210组窄带回波和1 210组宽带回波，对应维度分别为 $1 \times 101$ 和 $101 \times 101$ 。为进一步验证所提方法对噪声的稳健性，在原始窄带和宽带回波中分别加入高斯噪声，从而获得0 dB, 5 dB, 10 dB, 15 dB和20 dB的信噪比(Signal to Noise Ratio, SNR)。在此基础上，进一步得到对应的JTF,HRRP序列和RID像。

表 1 4类目标微动参数

目标	俯仰角(°)	自旋频率(Hz)	进动频率(Hz)	进动角(°)
目标1	21～30	3.0	2.0～4.0	4.0～5.5
目标2	21～30	1.5	1.5～3.5	2.0～3.5
目标3	21～30	2.0	1.0～3.0	3.0～4.5
目标4	21～30	1.0	0.5～2.5	1.0～2.5

下载: 导出CSV

| 显示表格

本文按照初始俯仰角将数据集划分为训练集和测试集^[17]。具体而言，取初始俯仰角21°～25°对应的样本作为训练集，可得到2 420个训练样本；取初始俯仰角26°～30°对应的样本作为测试集，可得到2 420个测试样本。

4.2 实验设置

采用反向传播方法^[21]训练特征提取网络、SAE网络和识别网络。为加快网络收敛速度并减少存储空间，采用包含动量机制和权值衰减技术的SGD(Stochastic Gradient Descent)优化器^[22]进行参数更新，更新公式如下

${{\boldsymbol{w}}^{\left( {\tau + 1} \right)}} = {{\boldsymbol{w}}^{\left( \tau \right)}} + \Delta {{\boldsymbol{w}}^{\left( {\tau + 1} \right)}}$

(12)

$\Delta {{\boldsymbol{w}}^{\left( {\tau + 1} \right)}} = \alpha \Delta {{\boldsymbol{w}}^{\left( \tau \right)}} - \beta {\eta _\tau }{{\boldsymbol{w}}^{\left( \tau \right)}} - {\eta _\tau }\nabla L\left( {{{\boldsymbol{w}}^{\left( \tau \right)}}} \right)$

(13)

其中， ${{\boldsymbol{w}}^{\left( {\tau + 1} \right)}}$ 是第 $\tau {\text{ + }}1$ 次迭代时的网络参数， ${{\boldsymbol{w}}^{\left( \tau \right)}}$ 是第 $\tau$ 次迭代时的网络参数， $\Delta {{\boldsymbol{w}}^{\left( \tau \right)}}$ 是第 $\tau$ 次迭代时 ${\boldsymbol{w}}$ 的变化量， $\alpha$ 为动量系数， $\beta$ 为权值衰减系数， $\nabla L\left( {{{\boldsymbol{w}}^{\left( \tau \right)}}} \right)$ 为代价函数 $L\left( {{{\boldsymbol{w}}^{\left( \tau \right)}}} \right)$ 第 $\tau$ 次迭代时对 ${\boldsymbol{w}}$ 的导数。 ${\eta _\tau }$ 为第 $\tau$ 次迭代时的学习率，并且以指数形式衰减

${\eta _\tau } = {\eta _0} \times {d^{\frac{\tau }{{{\rm{tb}}}}}}$

(14)

其中， ${\eta _0}$ 为初始学习率， $d$ 为衰减因子， $\tau$ 为当前迭代次数， ${\rm{tb}}$ 是总迭代次数。

在训练各网络模块时，相应超参数如所示，表中 $\alpha$ 为动量系数， $\beta$ 为权值衰减系数， ${\eta _0}$ 为初始学习率， $d$ 为衰减因子， ${{\rm{tb}}}$ 是总迭代次数。同时，批处理(Batch Size)大小均设置为64。

表 2 网络超参数

网络模块	SGD优化器		学习率		迭代次数	批处理大小
网络模块	$\alpha$	$\beta$	${\eta _0}$	$d$	${{\rm{tb}}}$	Batch Size
特征提取	0.5	0.01	0.1	0.94	50	64
SAE	0.5	0.001	0.1	0.96	50	64
识别网络	0.5	0	0.1	0.94	50	64

下载: 导出CSV

| 显示表格

4.3 实验结果

当SNR为0 dB, 5 dB, 10 dB, 15 dB和20 dB时，所提方法识别结果如表3所示。可以看出，SNR为20 dB时，识别率为97.64%，SNR为0 dB时，识别率为95.00%，性能下降较少，从而证明所提方法的有效性及噪声稳健性。

表 3 所提方法在各SNR下识别结果(%)

实验结果	SNR(dB)
实验结果	0	5	10	15	20
识别率	95.00	96.69	97.27	97.52	97.64

下载: 导出CSV

| 显示表格

为进一步验证所提方法相较于单一回波识别方法的优越性，表4列出不同SNR下所提方法与基于JTF, HRRP序列及RID像等单一回波识别方法的准确率对比。可以看出，所提方法的识别率最小可提升8.59%, 7.23%, 6.69%, 5.78%, 5.00%，从而证明其优越性。

表 4 所提方法与单一回波识别结果对比(%)

识别特征	SNR(dB)
识别特征	0	5	10	15	20
JTF	86.41	89.46	90.58	91.74	92.64
HRRP	86.00	86.74	88.84	88.93	89.96
RID	85.58	87.40	88.10	88.51	88.64
所提方法	95.00	96.69	97.27	97.52	97.64

下载: 导出CSV

| 显示表格

为了证明所提特征融合方法的有效性，与两种常见的特征级融合识别方法进行对比。第1种方法将所提取的3个深层特征直接进行拼接，然后输入分类层得到识别结果。第2种方法将所提取的3个深层特征相加，然后输入分类层得到识别结果。由于提取初级特征的维度不同，因此在相加之前先将不同模态的初级特征映射到同一维度。识别结果如表5所示，可以看出，所提算法相较于传统特征级融合方法的识别率均有不同程度的提升。

表 5 实验对比结果(%)

融合方法	SNR(dB)
融合方法	0	5	10	15	20
特征拼接	92.93	93.93	94.01	94.26	95.79
特征相加	92.31	93.76	94.05	94.17	95.95
所提方法	95.00	96.69	97.27	97.52	97.64

下载: 导出CSV

| 显示表格

5. 结束语

为充分挖掘利用微动目标宽、窄带雷达回波中蕴含的丰富信息，提出基于SAE的空间微动目标特征级融合识别方法。在训练阶段，首先采用CNN提取HRRP, JTF和RID像的层级特征，进而对深层特征进行拼接以获得联合特征向量。随后，采用SAE无监督地学习出联合特征向量的隐层特征，进而剔除SAE解码器部分并在编码器后接入Softmax分类器构成识别网络。最后，利用SAE网络参数对识别网络进行初始化，并利用联合特征向量对其微调以得到训练好的识别网络。在测试阶段，用训练好的CNN提取测试样本的联合特征向量，并直接输入训练好的识别网络以得到目标类别标签。各种条件下的电磁仿真数据识别结果表明，与仅采用单一回波的识别方法相比，所提方法能显著提升识别正确率并表现出噪声稳健性。未来将进一步研究观测样本不足条件下的空间微动目标小样本融合识别方法。

图 1 Morse信号时频图

下载: 全尺寸图片幻灯片

图 2 神经网络结构

下载: 全尺寸图片幻灯片

图 3 特征序列与时频图的对应

下载: 全尺寸图片幻灯片

图 4 多模型识别准确率对比

下载: 全尺寸图片幻灯片

图 5 多模型识别速度对比

下载: 全尺寸图片幻灯片

图 6 出现频率漂移和码长偏差的Morse信号

下载: 全尺寸图片幻灯片

表 1 CNN层设置

层名称	对应核大小
卷积层1	(5, 5, 1, 32)，步长=(1, 1)
最大池化层1	(2, 2)，步长=(2, 2)
卷积层2	(5, 5, 32, 64)，步长=(1, 1)
最大池化层2	(2, 16)，步长=(2, 2)

下载: 导出CSV

表 2 数据集组成

	码速(wpm)	信噪比(dB)	数目
训练集	25, 30, 40	40, 30, 20, 10, 6, 3, –3, –6, –8, –10	25000/50000
验证集	25, 30, 40	40, 30, 20, 10, 6, 3, –3, –6, –8, –10	2500
测试集	25, 30, 40	40, 30, 20, 10, 6, 3, –3, –6, –8, –10	2500

下载: 导出CSV

表 3 频率漂移和码长偏差情况下的译码准确率

	字准确率(%)	词准确率(%)
原始信号	99.92	99.65
频率漂移	96.23	91.71
频率漂移+码长偏差	95.88	90.40

下载: 导出CSV

表 4 有无频漂时去掉CNN前后译码性能

	迭代次数	字准确率(%)	词准确率(%)
有CNN，无频漂	23	99.92	99.65
无CNN，无频漂	42	92.71	73.90
有CNN，有频漂	26	96.23	91.71
无CNN，有频漂	47	63.11	20.35

下载: 导出CSV

参考文献(17)

DEY S, CHUGG K M, and BEEREL P A. Morse code datasets for machine learning[C]. The 9th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Bangalore, India, 2018: 1–7. doi: 10.1109/icccnt.2018.8494011.

SHIH C H and LUO C H. A Morse-code recognition system with LMS and matching algorithms for persons with disabilities[J]. International Journal of Medical Informatics, 1997, 44(3): 193–202. doi: 10.1016/s1386-5056(97)00020-8

HSIEH M C, LUO C H, and MAO Chiwu. Unstable Morse code recognition with adaptive variable-ratio threshold prediction for physically disabled persons[J]. IEEE Transactions on Rehabilitation Engineering, 2000, 8(3): 405–413. doi: 10.1109/86.867882

YANG Chenghong, LUO C H, JEANG Y L, et al. A novel approach to adaptive Morse code recognition for disabled persons[J]. Mathematics and Computers in Simulation, 2000, 54(1/3): 23–32. doi: 10.1016/s0378-4754(00)00180-4

GOLD B. Machine recognition of hand-sent Morse code[J]. IRE Transactions on Information Theory, 1959, 5(1): 17–24. doi: 10.1109/TIT.1959.1057478

WU Chungmin and LUO Chinghsing. Morse code recognition system with fuzzy algorithm for disabled persons[J]. Journal of Medical Engineering & Technology, 2002, 26(5): 202–207. doi: 10.1080/03091900210156904

WANG Yaqi, SUN Zhonghua, and JIA Kebin. An automatic decoding method for Morse signal based on clustering algorithm[C]. The 12th International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kaohsiung, China, 2017: 235–242.

王亚琦, 孙中华, 贾克斌. Morse报自动译码算法研究[J]. 信号处理, 2017, 33(11): 1451–1456.

WANG Yaqi, SUN Zhonghua, and JIA Kebin. Research on automatic decoding algorithm of Morse telegraph[J]. Signal Processing, 2017, 33(11): 1451–1456.

LECUN Y, BENGIO Y, and HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444. doi: 10.1038/nature14539

WANG Xianyu, ZHAO Qi, MA Cheng, et al. Automatic Morse code recognition under low SNR[C]. 2018 International Conference on Mechanical, Electronic, Control and Automation Engineering (MECAE 2018), Qingdao, China, 2018: 46–51. doi: 10.2991/mecae-18.2018.46.

SHI Baoguang, BAI Xiang, and YAO Cong. An end-to-end trainable neural network for image-based sequence recognition and its application to scene text recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(11): 2298–2304. doi: 10.1109/TPAMI.2016.2646371

韦醒超. 摩尔斯短波无线通信系统的设计与实现研究[D]. [硕士论文], 湖南大学, 2017.

WEI Xingchao. Research on the design and implementation of Morse shortwave wireless communication system[D]. [Master dissertation], Hunan University, 2017.

CABAL-YEPEZ E, GARCIA-RAMIREZ A G, ROMERO-TRONCOSO R J, et al. Reconfigurable monitoring system for time-frequency analysis on industrial equipment through STFT and DWT[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 760–771. doi: 10.1109/TII.2012.2221131

SAINATH T N, KINGSBURY B, SAON G, et al. Deep convolutional neural networks for large-scale speech tasks[J]. Neural Networks, 2015, 64: 39–48. doi: 10.1016/j.neunet.2014.08.005

GRAVES A and SCHMIDHUBER J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures[J]. Neural Networks, 2005, 18(5/6): 602–610. doi: 10.1016/j.neunet.2005.06.042

GRAVES A, FERNÁNDEZ S, and GOMEZ F. Connectionist temporal classification: Labelling unsegmented sequence data with recurrent neural networks[C]. The 23rd International Conference on Machine Learning, Pittsburgh, USA, 2006: 369–367.

刘宏哲, 杨少鹏, 袁家政, 等. 基于单一神经网络的多尺度人脸检测[J]. 电子与信息学报, 2018, 40(11): 2598–2605. doi: 10.11999/JEIT180163

LIU Hongzhe, YANG Shaopeng, YUAN Jiazheng, et al. Multi-scale face detection based on single neural network[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2598–2605. doi: 10.11999/JEIT180163

施引文献

资源附件(0)

访问统计

图(6) / 表(4)

计量

文章访问数: 3997
HTML全文浏览量: 1186
PDF下载量: 178
被引次数: 0

1. 引言
2. 建模
2.1 微动建模
2.2 信号建模
2.3 预处理
3. 所提算法
3.1 基于CNN的特征提取
3.2 基于SAE的融合识别
4. 实验设置
4.1 数据集设置
4.2 实验设置
4.3 实验结果
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于深度神经网络的Morse码自动译码算法

doi: 10.11999/JEIT190658

通讯作者:
李伟浩　liweihao315@gmail.com

计量

Automatic Decoding Algorithm of Morse Code Based on Deep Neural Network

1. 引言

2. 建模

2.1 微动建模

2.2 信号建模

2.3 预处理

3. 所提算法

3.1 基于CNN的特征提取

3.2 基于SAE的融合识别

4. 实验设置

4.1 数据集设置

4.2 实验设置

4.3 实验结果

5. 结束语

计量

目录

1. 引言

2. 建模

2.1 微动建模

2.2 信号建模

2.3 预处理

3. 所提算法

3.1 基于CNN的特征提取

3.2 基于SAE的融合识别

4. 实验设置

4.1 数据集设置

4.2 实验设置

4.3 实验结果

5. 结束语

留言板

基于深度神经网络的Morse码自动译码算法

doi: 10.11999/JEIT190658

通讯作者: 李伟浩 liweihao315@gmail.com

计量

出版历程

Automatic Decoding Algorithm of Morse Code Based on Deep Neural Network

1. 引言

2. 建模

2.1 微动建模

2.2 信号建模

2.3 预处理

3. 所提算法

3.1 基于CNN的特征提取

3.2 基于SAE的融合识别

4. 实验设置

4.1 数据集设置

4.2 实验设置

4.3 实验结果

5. 结束语

计量

出版历程

目录

1. 引言

2. 建模

2.1 微动建模

2.2 信号建模

2.3 预处理

3. 所提算法

3.1 基于CNN的特征提取

3.2 基于SAE的融合识别

4. 实验设置

4.1 数据集设置

4.2 实验设置

4.3 实验结果

5. 结束语

通讯作者:
李伟浩　liweihao315@gmail.com