A Layered Decoding Algorithm for Spatially-coupled LDPC Codes
-
摘要:
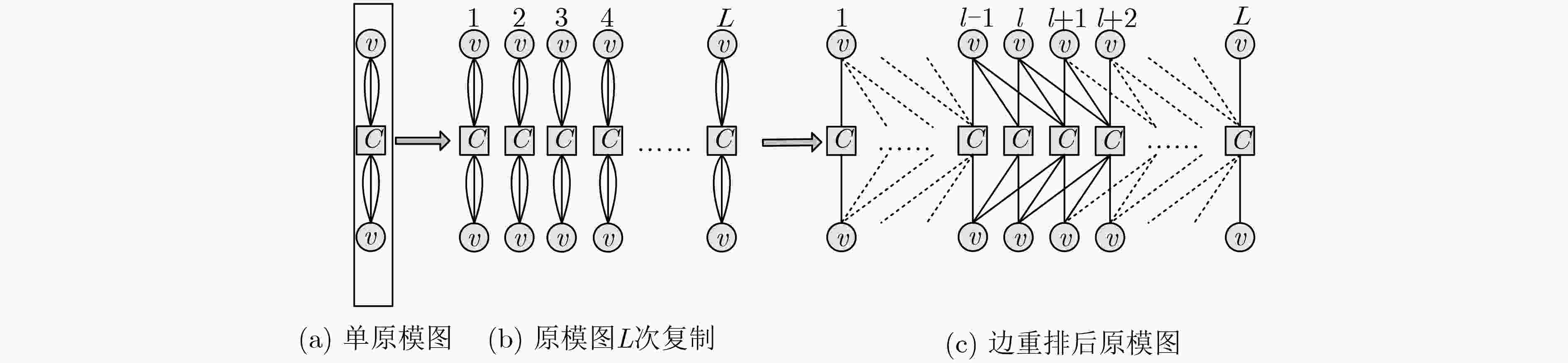
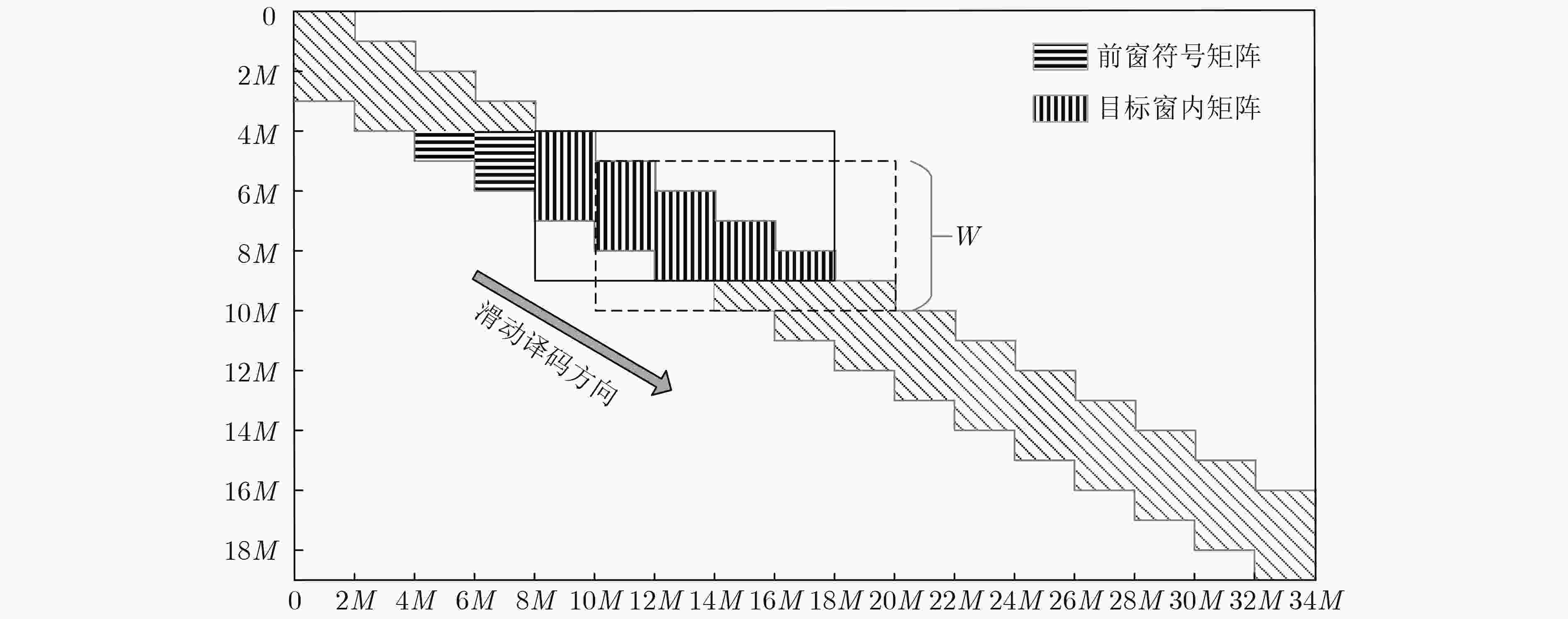
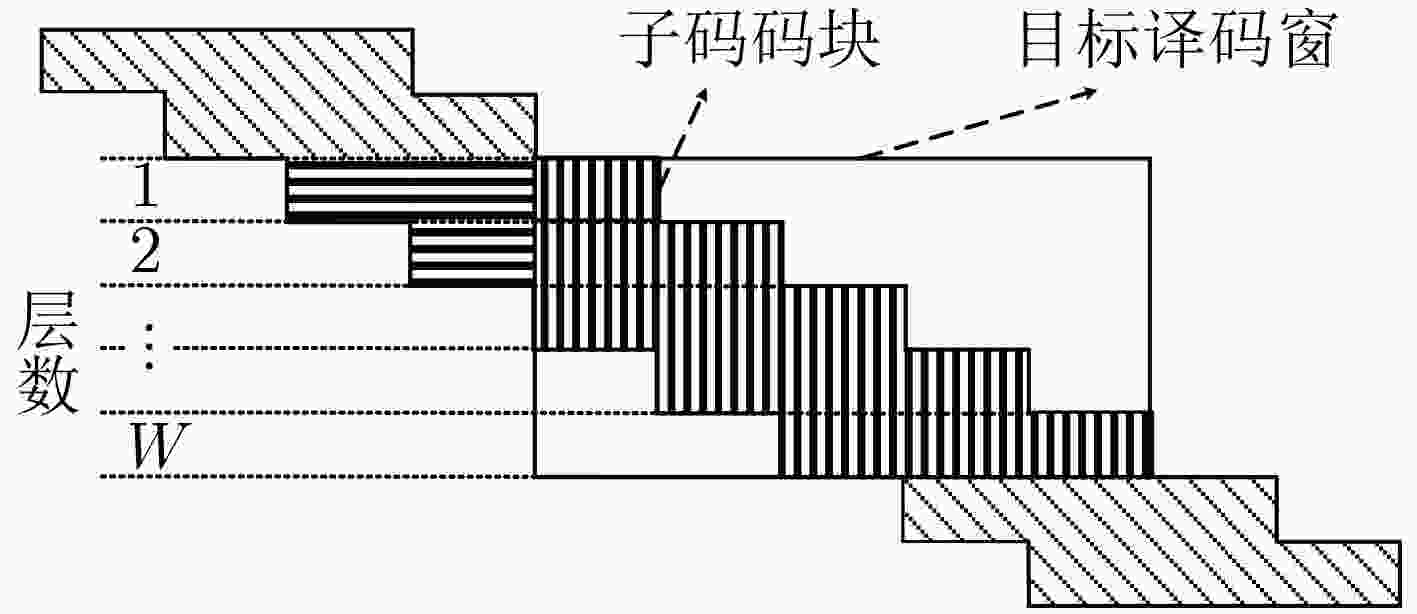
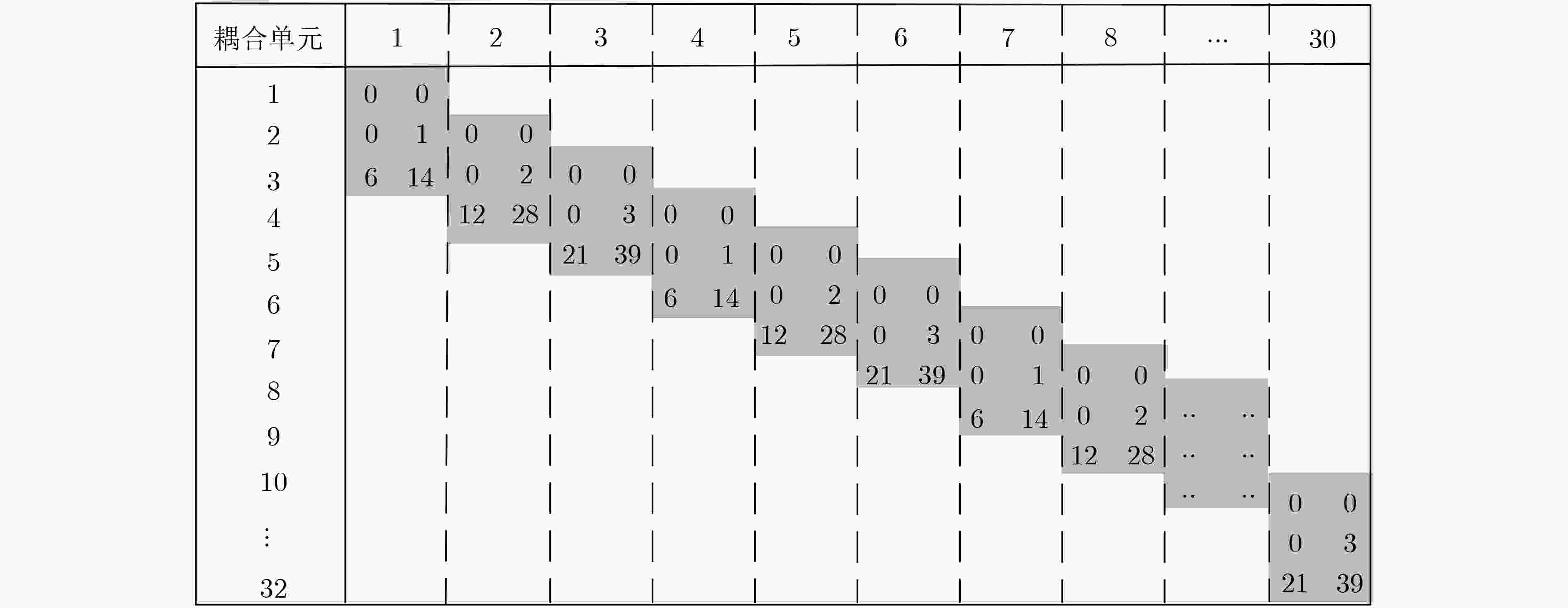
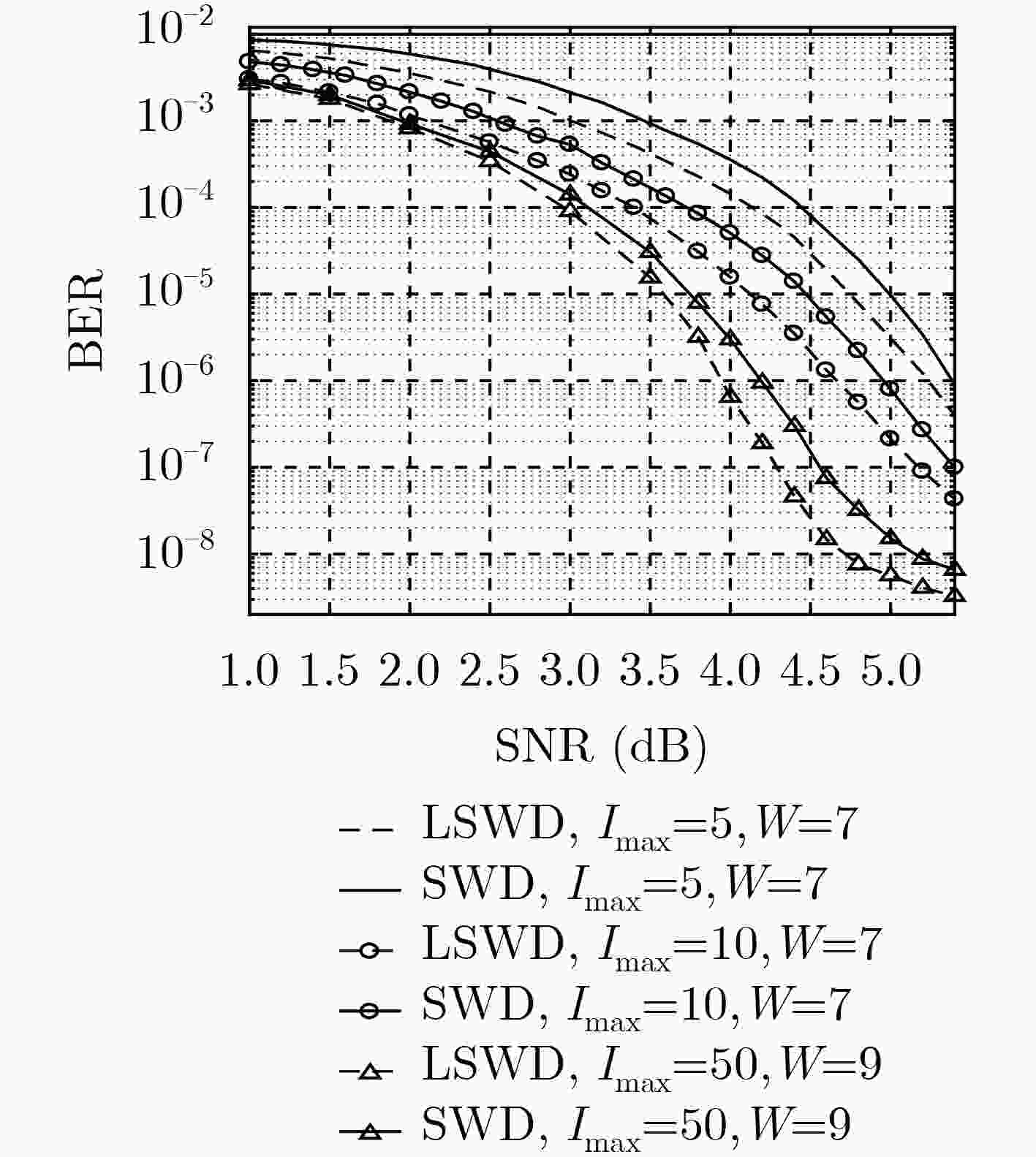
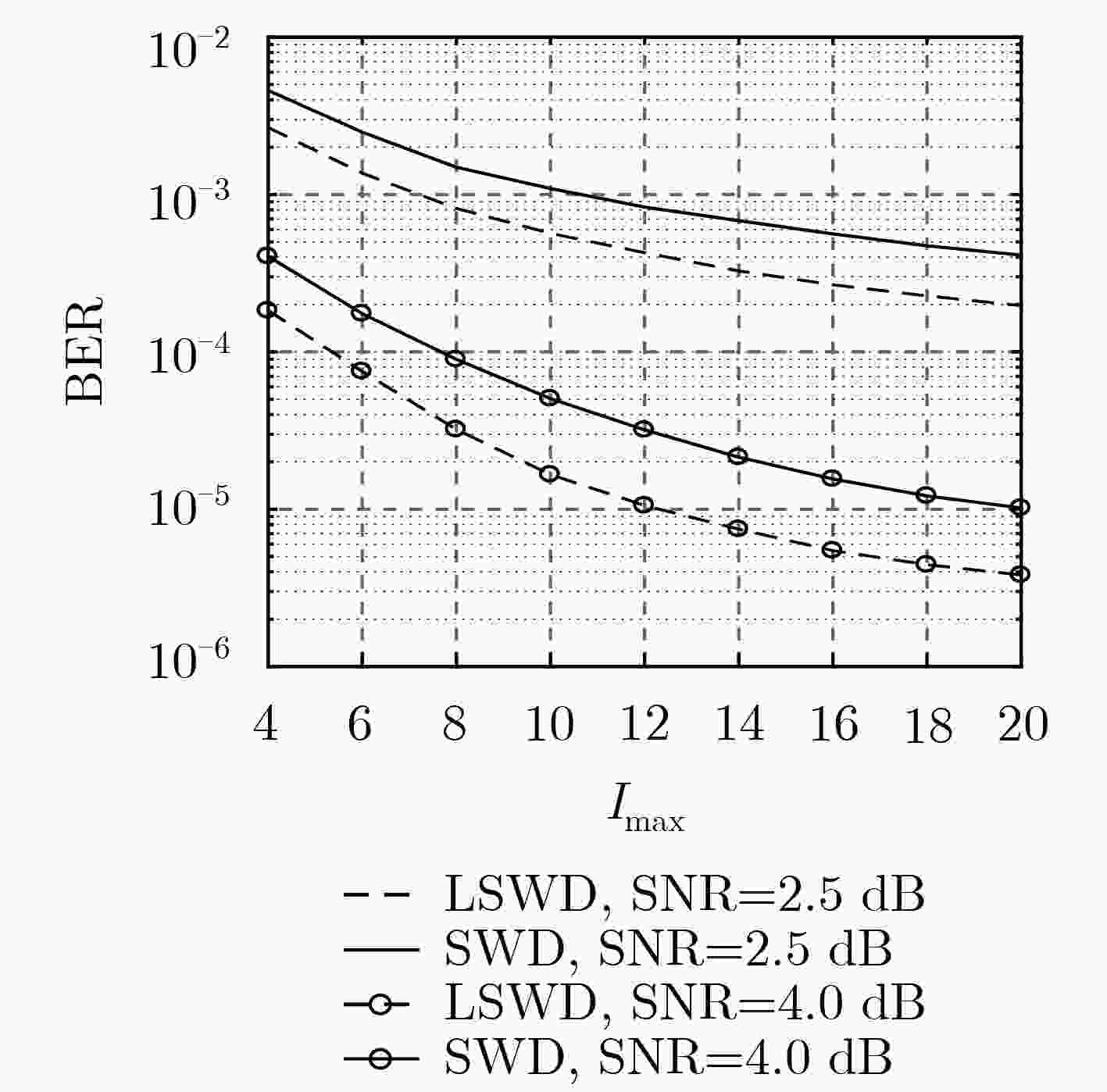
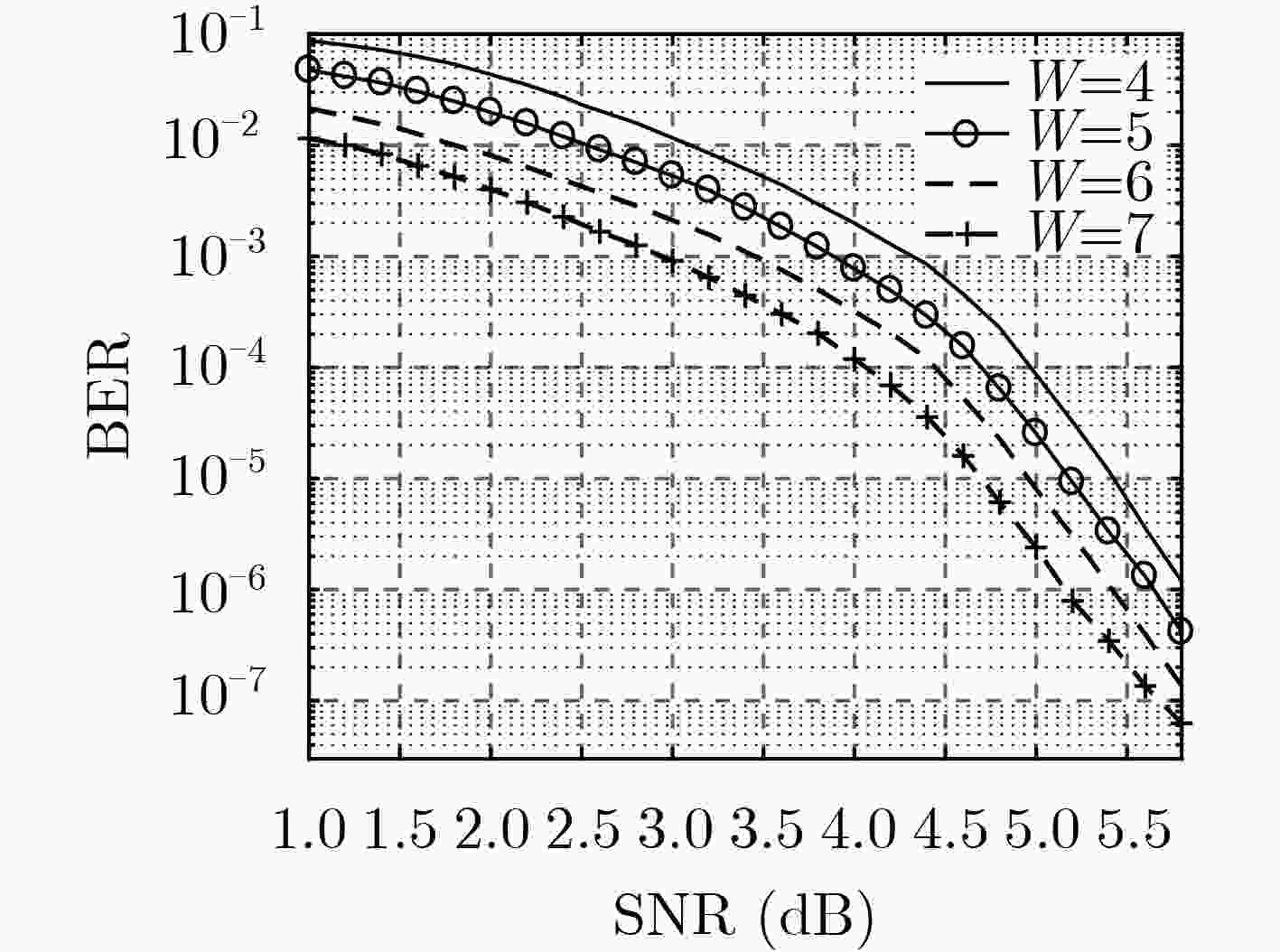
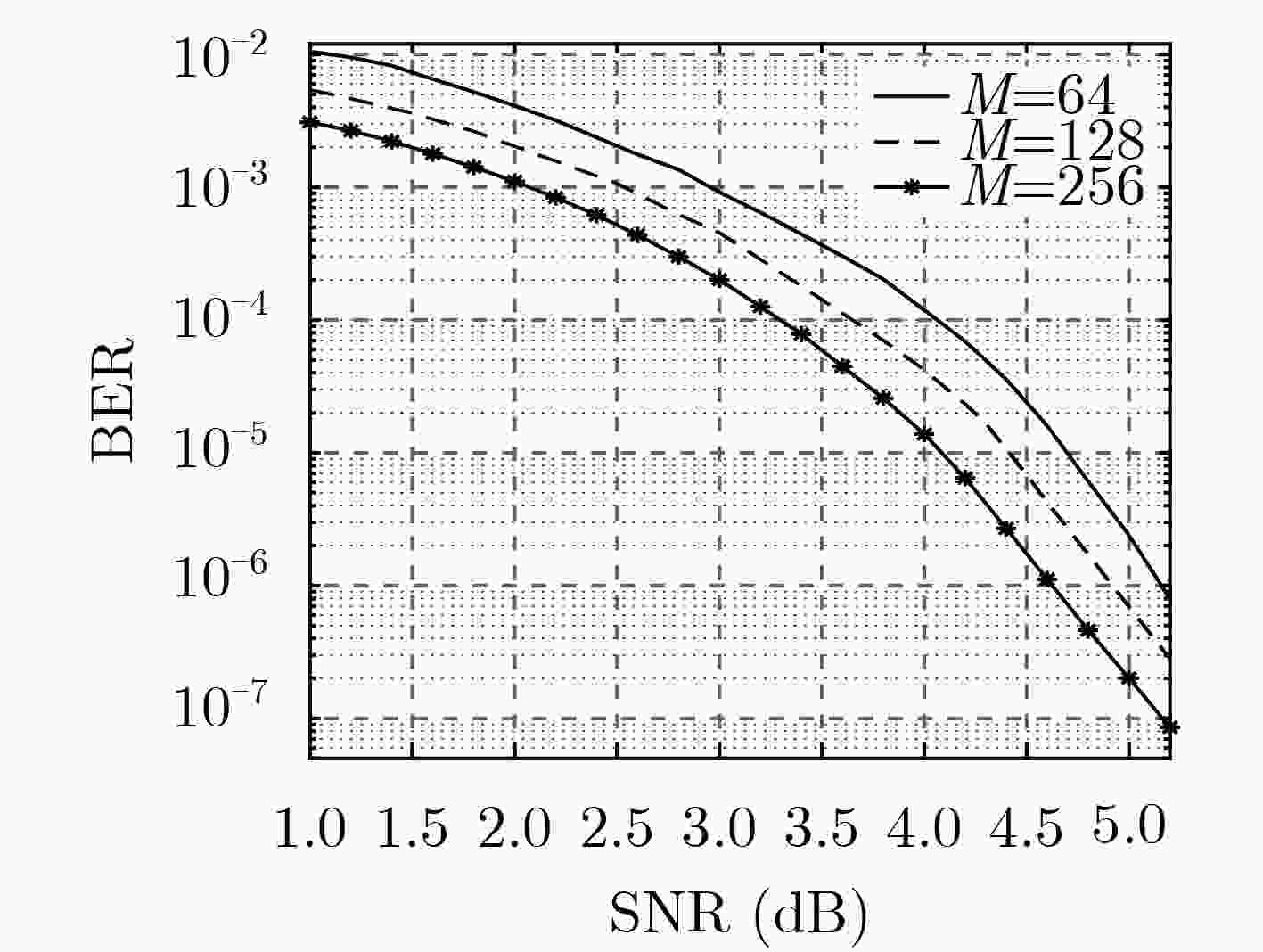
针对长码长空间耦合低密度奇偶校验(SC-LDPC)码译码时延较长的问题,该文提出了分层滑动窗译码(LSWD)算法。该算法利用SC-LDPC子码码块的准循环特性和滑动窗内校验矩阵的层次结构,通过在滑动窗内对校验矩阵进行分层处理,优化层与层之间消息传递,从而加快窗内译码的收敛速度,减少了译码迭代次数。仿真和分析结果表明:在相同的信噪比(SNR)条件和相同的误码性能要求下,LSWD算法所需的迭代次数少于滑动窗译码(SWD)算法,特别在高信噪比下,LSWD算法的迭代次数约为SWD算法的一半,从而有效缩短全局译码时延;在相同译码迭代次数下,LSWD算法的译码性能优于SWD算法,而其计算复杂度增加不大。
-
关键词:
- 空间耦合低密度奇偶校验码 /
- 分层算法 /
- 译码延时 /
- 滑动窗
Abstract:In order to solve the problem of the long decoding delay for the Spatially-Coupled Low-Density Parity-Check (SC-LDPC) code with long code length, a Layered Sliding Window Decoding (LSWD) algorithm is proposed. By exploring the quasi-cyclic characteristics of the SC-LDPC sub-codeblock and the hierarchical structure of the check matrix in the sliding window, the part of check matrix in the sliding window is layered to optimize the message transfer between two neighbor layers, with the aim of accelerating the convergence of the iterative procedure and reducing the number of decoding iterations. Simulation and analysis results show that the number of iterations in the proposed LSWD algorithm is less than that in the SWD, under the same Signal-to-Noise Ratio (SNR) and the bit error ratio. In the high SNR region, especially, the number of iterations in the proposed LSWD is about half of that in the SWD, hence the global decoding delay of the former is effectively shorten. In addition, the decoding performance of the LSWD algorithm is better than the SWD algorithm under the same number of decoding iterations, and the overall computational complexity is slightly increased.
-
表 1 译码算法单次迭代过程的计算量比较
译码算法 加法运算 $\phi (x)$运算 SWD ${K_g} \times M \times W \times (J + K + 1)$ $2{K_g} \times M \times W \times J$ LSWD ${K_g} \times M \times W \times (2J + K + 1)$ $2{K_g} \times M \times W \times J$ -
KUDEKAR S, RICHARDSON T, and URBANKE R L. Spatially coupled ensembles universally achieve capacity under belief propagation[J]. IEEE Transactions on Information Theory, 2013, 59(12): 7761–7813. doi: 10.1109/TIT.2013.2280915 IYENGAR A R, PAPALEO M, SIEGEL P H, et al. Windowed decoding of protograph-based LDPC convolutional codes over erasure channels[J]. IEEE Transactions on Information Theory, 2012, 58(4): 2303–2320. doi: 10.1109/TIT.2011.2177439 SCHWANDTER S, AMAT A G I, and MATZ G. Spatially-coupled LDPC codes for decode-and-forward relaying of two correlated sources over the BEC[J]. IEEE Transactions on Communications, 2014, 62(4): 1324–1337. doi: 10.1109/TCOMM.2014.020514.130317 MITCHELL D G M, LENTMAIER M, and COSTELLO D J. Spatially coupled LDPC codes constructed from protographs[J]. IEEE Transactions on Information Theory, 2015, 61(9): 4866–4889. doi: 10.1109/TIT.2015.2453267 XIE Yixuan, YANG Lei, KANG Peng, et al. Euclidean geometry-based spatially coupled LDPC codes for storage[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(9): 2498–2509. doi: 10.1109/JSAC.2016.2603703 贺文武, 夏巧桥, 邹炼. 基于变量节点更新的交替方向乘子法LDPC惩罚译码算法[J]. 电子与信息学报, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358HE Wenwu, XIA Qiaoqiao, and ZOU Lian. Alternating direction method of multipliers LDPC penalized decoding algorithm based on variable node update[J]. Journal of Electronics &Information Technology, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358 IYENGAR A R, SIEGEL P H, URBANKE R L, et al. Windowed decoding of spatially coupled codes[J]. IEEE Transactions on Information Theory, 2013, 59(4): 2277–2292. doi: 10.1109/TIT.2012.2231465 KANG Peng, XIE Yixuan, YANG Lei, et al. Reliability-based windowed decoding for spatially coupled LDPC codes[J]. IEEE Communications Letters, 2018, 22(7): 1322–1325. doi: 10.1109/LCOMM.2018.2835466 ABU-SURRA S, PISEK E, and TAORI R. Spatially-coupled low-density parity check codes: zigzag-window decoding and code-family design considerations[C]. Information Theory and Applications Workshop, San Diego, USA, 2015: 275-281. doi: 10.1109/ITA.2015.7309001. SCHLÜTER M, HASSAN N U, and FETTWEIS G P. On the construction of protograph based SC-LDPC codes for windowed decoding[C]. 2018 IEEE Wireless Communications and Networking Conference, Barcelona, Spain, 2018: 15–18. doi: 10.1109/WCNC.2018.8377289. ALI I, KIM J H, KIM S H, et al. Improving windowed decoding of SC LDPC codes by effective decoding termination, message reuse, and amplification[J]. IEEE Access, 2017, 6: 9336–9346. doi: 10.1109/ACCESS.2017.2771375 TADAYON M H, TASDIGHI A, BATTAGLIONI M, et al. Efficient search of compact QC-LDPC and SC-LDPC convolutional codes with large girth[J]. IEEE Communications Letters, 2018, 22(6): 1156–1159. doi: 10.1109/LCOMM.2018.2827959 穆丽伟, 刘星成, 张涵. 高性能时不变LDPC卷积码构造算法研究[J]. 电子与信息学报, 2016, 38(9): 2274–2279. doi: 10.11999/JEIT151376MU Liwei, LIU Xingcheng, and ZHANG Han. New ensemble of time-invariant LDPC convolutional codes with high performance[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2274–2279. doi: 10.11999/JEIT151376 CHEN Xiaoheng, LIN Shu, and AKELLA V. QSN-a simple circular-shift network for reconfigurable quasi-cyclic LDPC decoders[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2010, 57(10): 782–786. doi: 10.1109/TCSII.2010.2067811 -





 下载:
下载:


 下载:
下载:
