Selective Ensemble Method of Extreme Learning Machine Based on Double-fault Measure
-
摘要: 极限学习机(ELM)具有学习速度快、易实现和泛化能力强等优点,但单个ELM的分类性能不稳定。集成学习可以有效地提高单个ELM的分类性能,但随着数据规模和基ELM数目的增加,计算复杂度会大幅度增加,消耗大量的计算资源。针对上述问题,该文提出一种基于双错测度的极限学习机选择性集成方法(DFSEE),同时从理论和实验的角度进行了详细分析。首先,运用bootstrap 方法重复抽取训练集,获得多个训练子集,在ELM上进行独立训练,得到多个具有较大差异性的基ELM,构成基ELM池;其次,计算出每个基ELM的双错测度,将基ELM按照双错测度的大小进行升序排序;最后,采用多数投票算法,根据顺序将基ELM逐个累加集成,直至集成精度最优,即获得基ELM最优子集成,并分析了其理论基础。在10个UCI数据集上的实验结果表明,较其他方法使用了更小规模的基ELM,获得了更高的集成精度,同时表明了其有效性和显著性。Abstract: Extreme Learning Machine (ELM) has unique advantages such as fast learning speed, simplicity of implementation, and excellent generalization performance. However, the performance of a single ELM is unstable in classification. Ensemble learning can effectively improve the classification ability of single ELMs, but it may incur the rapid increase in memory space and computational overheads as the increase of the data size and the number of ELMs. To address this issue, a Selective Ensemble approach of ELM based on Double-Fault measure (DFSEE) is proposed, and it is evaluated by theoretical and experimental analysis simultaneously. Firstly, multiple training subsets extracted from a training dataset are obtained employing the bootstrap sampling method, and an initial pool of base ELMs is constructed by independently training multiple ELMs on different training subsets; Secondly, the ELMs in pool are sorted in ascending order according to their double-fault measures of those ELMs. Finally, it starts with one ELM and grows the ensemble by adding new base ELMs according to the order, the final ensemble of ELMs can be achieved with the best classification ability, and the theoretical basis of DFSEE is analyzed. Experimental results on 10 benchmark classification tasks show that DFSEE can achieve better results with less number of ELMs by comparing with other approaches, and its validity and significance.
-
Key words:
- Selective ensemble /
- Double-fault measure /
- Extreme Learning Machine (ELM)
-
表 1 两个分类器的联合分布
${f_i}({x_k}) = {y_k}$ ${f_i}({x_k}) \ne {y_k}$ ${f_j}({x_k}) = {y_k}$ $a$ $b$ ${f_j}({x_k}) \ne {y_k}$ $c$ $d$ 表 2 UCI数据集
数据集 实例个数 属性个数 类别 Heart 270 13 2 Cleveland 303 13 5 Bupa 345 6 2 Wholesale 440 7 2 Diabetes 768 8 2 German 1000 20 2 QSAR 1055 41 2 CMC 1473 9 3 Spambase 4601 57 2 Wineq-w 4898 11 7 表 3 在不同规模基ELM (100, 200, 300)下的集成分类准确率(%)
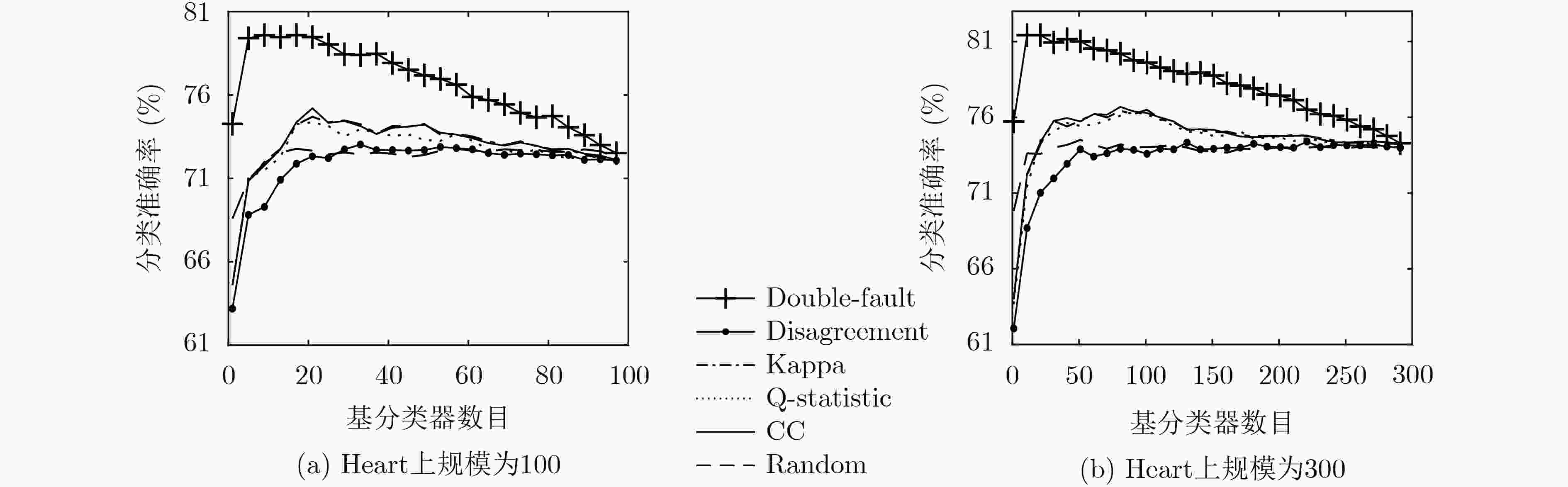
数据集 100 200 300 DFSEE 最高 平均 最低 DFSEE 最高 平均 最低 DFSEE 最高 平均 最低 Heart 80.48 75.00 63.60 51.14 82.48 76.33 63.63 49.24 82.24 76.57 63.68 48.57 Cleveland 57.01 55.87 48.66 38.86 57.61 56.62 48.68 38.11 57.91 56.82 48.68 37.71 Bupa 75.37 70.67 60.21 48.18 76.95 71.51 60.15 47.09 77.40 72.18 60.23 46.49 Wholesale 94.04 89.56 82.78 74.19 94.78 90.26 82.78 73.48 95.15 90.59 82.73 73.04 Diabetes 71.88 70.62 61.83 52.64 73.10 71.49 61.73 51.03 73.77 71.81 61.74 50.65 German 77.40 75.17 69.61 63.63 78.08 76.12 69.63 62.83 78.58 76.40 69.64 62.62 QSAR 86.26 82.67 74.45 65.63 87.78 83.63 74.52 64.92 88.28 83.89 74.49 63.98 CMC 62.99 60.45 54.21 46.57 63.41 61.03 54.25 45.92 63.88 61.33 54.23 45.46 Spambase 80.78 77.57 70.13 63.32 81.55 78.17 70.12 62.79 81.70 78.42 70.13 62.53 Wineq-w 51.38 50.80 46.97 44.52 51.73 51.03 46.94 44.21 51.90 51.20 46.94 44.07 表 4 在不同规模基ELM (100, 200, 300)下DFSEE与Bagging分类准确率对比分析(%)
数据集 100 200 300 Bagging 本文DFSEE n Bagging 本文DFSEE n Bagging 本文DFSEE n Heart 72.10 80.48 13 71.67 82.48 11 71.71 82.24 11 Cleveland 49.25 57.01 4 49.25 57.61 6 49.25 57.91 6 Bupa 65.61 75.37 12 64.14 76.95 12 64.98 77.40 15 Wholesale 86.44 94.04 8 86.00 94.78 10 86.11 95.15 11 Diabetes 63.79 71.88 7 63.51 73.10 7 63.63 73.77 8 German 74.13 77.40 14 74.40 78.08 9 74.38 78.58 9 QSAR 80.22 86.26 9 80.41 87.78 8 80.47 88.28 9 CMC 58.22 62.99 9 58.44 63.41 12 58.45 63.88 13 Spambase 73.34 80.78 12 73.37 81.55 13 73.46 81.70 11 Wineq-w 46.58 51.38 8 46.57 51.73 11 46.56 51.90 14 表 5 与其他方法在集成精度(%)和集成规模方面对比分析(基ELM规模200)
数据集 本文DFSEE n AGOB n POBE n MOAG n EP-FP n SCG-P n Heart 82.48 11 74.14 49 77.52 96 74.86 43 74.38 95 75.24 38 Cleveland 57.61 6 54.43 22 51.09 132 50.85 25 49.25 95 56.25 1 Bupa 76.95 12 69.93 37 72.95 99 69.47 59 65.89 66 76.89 48 Wholesale 94.78 10 89.67 36 92.74 99 88.59 27 86.11 96 87.85 9 Diabetes 73.10 7 66.03 26 68.99 102 66.27 52 63.73 89 65.30 58 German 78.08 9 75.15 36 76.60 96 75.30 38 74.47 86 75.18 54 QSAR 87.78 8 83.48 24 84.37 100 83.94 32 80.43 88 82.02 37 CMC 63.41 12 59.63 47 60.92 103 59.67 51 58.46 97 59.51 67 Spambase 81.55 13 76.18 32 79.12 97 76.47 67 76.64 93 76.66 58 Wineq-w 51.73 11 50.37 23 49.48 93 48.10 34 48.60 96 50.98 46 表 6 与其他方法在运行时间方面的对比分析(s)
数据集 本文DFSEE AGOB POBE MOAG EP-FP SCG-P Heart 0.80 10.96 0.79 0.87 18.24 0.86 Cleveland 0.77 22.36 0.73 1.10 2.77 1.10 Bupa 0.86 13.97 0.85 0.95 41.26 0.95 Wholesale 1.16 17.26 1.15 1.27 21.97 1.26 Diabetes 1.29 17.95 1.28 1.40 30.40 1.39 German 1.79 12.58 1.78 1.86 11.58 1.86 QSAR 2.29 14.01 2.29 2.37 23.55 2.37 CMC 2.25 24.44 2.21 2.62 30.85 2.61 Spambase 8.54 43.86 8.52 8.80 110.46 8.78 Wineq-w 7.71 79.18 7.58 8.85 48.56 8.82 -
HUANG Guangbin, ZHU Qinyu, and SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. doi: 10.1016/j.neucom.2005.12.126 YANG Yifan, ZHANG Hong, YUAN D, et al. Hierarchical extreme learning machine based image denoising network for visual Internet of Things[J]. Applied Soft Computing, 2019, 74: 747–759. doi: 10.1016/j.asoc.2018.08.046 吴超, 李雅倩, 张亚茹, 等. 用于表示级特征融合与分类的相关熵融合极限学习机[J]. 电子与信息学报, 2020, 42(2): 386–393. doi: 10.11999/JEIT190186WU Chao, LI Yaqian, ZHANG Yaru, et al. Correntropy-based fusion extreme learning machine for representation level feature fusion and classification[J]. Journal of Electronics &Information Technology, 2020, 42(2): 386–393. doi: 10.11999/JEIT190186 陆慧娟, 安春霖, 马小平, 等. 基于输出不一致测度的极限学习机集成的基因表达数据分类[J]. 计算机学报, 2013, 36(2): 341–348. doi: 10.3724/SP.J.1016.2013.00341LU Huijuan, AN Chunlin, MA Xiaoping, et al. Disagreement measure based ensemble of extreme learning machine for gene expression data classification[J]. Chinese Journal of Computers, 2013, 36(2): 341–348. doi: 10.3724/SP.J.1016.2013.00341 LAN Y, SOH Y C, and HUANG Guangbin. Ensemble of online sequential extreme learning machine[J]. Neurocomputing, 2009, 72(13/15): 3391–3395. doi: 10.1016/j.neucom.2009.02.013 KSIENIEWICZ P, KRAWCZYK B, and WOŹNIAK M M. Ensemble of Extreme Learning Machines with trained classifier combination and statistical features for hyperspectral data[J]. Neurocomputing, 2018, 271: 28–37. doi: 10.1016/j.neucom.2016.04.076 李炜, 李全龙, 刘政怡. 基于加权的K近邻线性混合显著性目标检测[J]. 电子与信息学报, 2019, 41(10): 2442–2449. doi: 10.11999/JEIT190093LI Wei, LI Quanlong, and LIU Zhengyi. Salient object detection using weighted K-nearest neighbor linear blending[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2442–2449. doi: 10.11999/JEIT190093 YKHLEF H and BOUCHAFFRA D. An efficient ensemble pruning approach based on simple coalitional games[J]. Information Fusion, 2017, 34: 28–42. doi: 10.1016/j.inffus.2016.06.003 CAO Jingjing, LI Wenfeng, MA Congcong, et al. Optimizing multi-sensor deployment via ensemble pruning for wearable activity recognition[J]. Information Fusion, 2018, 41: 68–79. doi: 10.1016/j.inffus.2017.08.002 MARTÍNEZ-MUÑOZ G, HERNÁNDEZ-LOBATO D, and SUÁREZ A. An analysis of ensemble pruning techniques based on ordered aggregation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 245–259. doi: 10.1109/TPAMI.2008.78 MARTÍNEZ-MUÑOZ G and SUÁREZ A. Pruning in ordered bagging ensembles[C]. The 23rd International Conference on Machine learning, New York, USA, 2006: 609-616. doi: 10.1145/1143844.1143921. GUO Li and BOUKIR S. Margin-based ordered aggregation for ensemble pruning[J]. Pattern Recognition Letters, 2013, 34(6): 603–609. doi: 10.1016/j.patrec.2013.01.003 DAI Qun, ZHANG Ting, and LIU Ningzhong. A new reverse reduce-error ensemble pruning algorithm[J]. Applied Soft Computing, 2015, 28: 237–249. doi: 10.1016/j.asoc.2014.10.045 ZHOU Zhihua, WU Jianxin, and TANG Wei. Ensembling neural networks: Many could be better than all[J]. Artificial Intelligence, 2002, 137(1/2): 239–263. doi: 10.1016/S0004-3702(02)00190-X CAVALCANTI G D C, OLIVEIRA L S, MOURA T J M, et al. Combining diversity measures for ensemble pruning[J]. Pattern Recognition Letters, 2016, 74: 38–45. doi: 10.1016/j.patrec.2016.01.029 MAO Shasha, CHEN Jiawei, JIAO Licheng, et al. Maximizing diversity by transformed ensemble learning[J]. Applied Soft Computing, 2019, 82: 105580. doi: 10.1016/j.asoc.2019.105580 TANG E K, SUGANTHAN P N, and YAO Xin. An analysis of diversity measures[J]. Machine Learning, 2006, 65(1): 247–271. doi: 10.1007/s10994-006-9449-2 GIACINTO G and ROLI F. Design of effective neural network ensembles for image classification purposes[J]. Image and Vision Computing, 2001, 19(9/10): 699–707. doi: 10.1016/S0262-8856(01)00045-2 FUSHIKI T. Estimation of prediction error by using K-fold cross-validation[J]. Statistics and Computing, 2011, 21(2): 137–146. doi: 10.1007/s11222-009-9153-8 ZHOU Hongfa, ZHAO Xuehan, and WANG Xiao. An effective ensemble pruning algorithm based on frequent patterns[J]. Knowledge-Based Systems, 2014, 56: 79–85. doi: 10.1016/j.knosys.2013.10.024 -





 下载:
下载:


 下载:
下载:
