基于核稀疏编码的阵发性房颤检测

刘明; 孟宪辉; 熊鹏; 刘秀玲

doi:10.11999/JEIT190582

基于核稀疏编码的阵发性房颤检测

doi: 10.11999/JEIT190582

1.
河北大学电子信息工程学院保定 071002
2.
河北省数字医疗工程重点实验室保定 071002

基金项目: 国家自然科学基金(61673158)，河北省自然科学基金(F2018201070)，河北省研究生创新资助项目(CXZZSS2019006)，河北省青年拔尖人才项目(BJ2019044)

详细信息

作者简介:
刘明：男，1972年生，博士，副教授，研究方向为模式识别和心电信号处理

孟宪辉：女，1994年生，硕士生，研究方向为心电信号处理

熊鹏：女，1986年生，博士，讲师，研究方向为模式识别和生物信号处理

刘秀玲：女，1977年生，博士，教授，研究方向为生物医学成像和信号处理

通讯作者:
刘秀玲　liuxiuling121@hotmail.com

中图分类号: TP399
计量
- 文章访问数: 2106
- HTML全文浏览量: 1128
- PDF下载量: 50
- 被引次数: 0
出版历程
- 收稿日期: 2019-08-01
- 修回日期: 2020-03-04
- 网络出版日期: 2020-03-27
- 刊出日期: 2020-07-23

Detection of Paroxysmal Atrial Fibrillation Based on Kernel Sparse Coding

1.
College of Electronic and Information Engineering, Hebei University, Baoding 071002, China
2.
Key Laboratory of Digital Medical Engineering of Hebei Province, Baoding 071002, China

Funds: The National Natural Science Fundation of China (61673158), The Natural Science Foundation of Hebei Province (F2018201070), The Graduate Innovation Funding Project of Hebei Province (CXZZSS2019006), The Hebei Young Talent Project (BJ2019044)

摘要

摘要:
阵发性房颤(PAF)是一种具有偶发性的心律失常，其较高的漏检率导致心脏相关疾病的增加。该文提出了一种基于核稀疏编码的自动检测方法，可以仅根据较短RR间期数据识别PAF发作。该方法采用特殊几何结构来分析数据高维特性，通过计算协方差矩阵作为特征描述子，找到蕴含在数据中的黎曼流形结构；然后基于Log-Euclid框架，利用核方法将流形空间映射到高维可再生核希尔伯特空间，以获取更准确的稀疏表示来快速识别PAF。经麻省理工学院-贝斯以色列医院房颤数据库验证，获得98.71%的敏感性、98.43%的特异度和98.57%的总准确率。因此，该研究对检测短暂发作的PAF有实质性的改善，在临床监测和治疗方面显示出良好的潜力。
- 阵发性房颤 /
- 协方差描述子 /
- 黎曼流形 /
- 核稀疏编码
Abstract:
Paroxysmal Atrial Fibrillation (PAF) is a kind of accidental arrhythmia, and its high missed detection rate leads to the increase of heart-related diseases. An automatic detection method is proposed based on kernel sparse coding, which can identify PAF attacks based only on short RR interval data. A special geometric structure is presented to analyze the high-dimensional characteristics of the data, and the covariance matrix is calculated as a feature descriptor to find the Riemannian manifold structure contained in the data; Based on the Log-Euclidean framework, a manifold method is used to map the manifold space to a high-dimensional renewable kernel Hilbert space to obtain a more accurate sparse representation to identify quickly PAF. After verification by the Massa-chusetts Institute of Technology-Beth Israel Hospital atrial fibrillation database, the sensitivity is 98.71%, the specificity is 98.43%, and the total accuracy rate is 98.57%. Therefore, this study has a substantial improvement in the detection of transient PAF and shows good potential for clinical monitoring and treatment.
- Paroxysmal Atrial Fibrillation(PAF) /
- Covariance descriptor /
- Riemann manifold /
- Kernel sparse coding

HTML全文

图 1 PAF检测流程图

下载: 全尺寸图片幻灯片

图 2 PAF患者ECG记录的RR间期时间序列

下载: 全尺寸图片幻灯片

图 3 PAF参数变化的所需计算时间

下载: 全尺寸图片幻灯片

表 1 参数变化的检测性能(%)

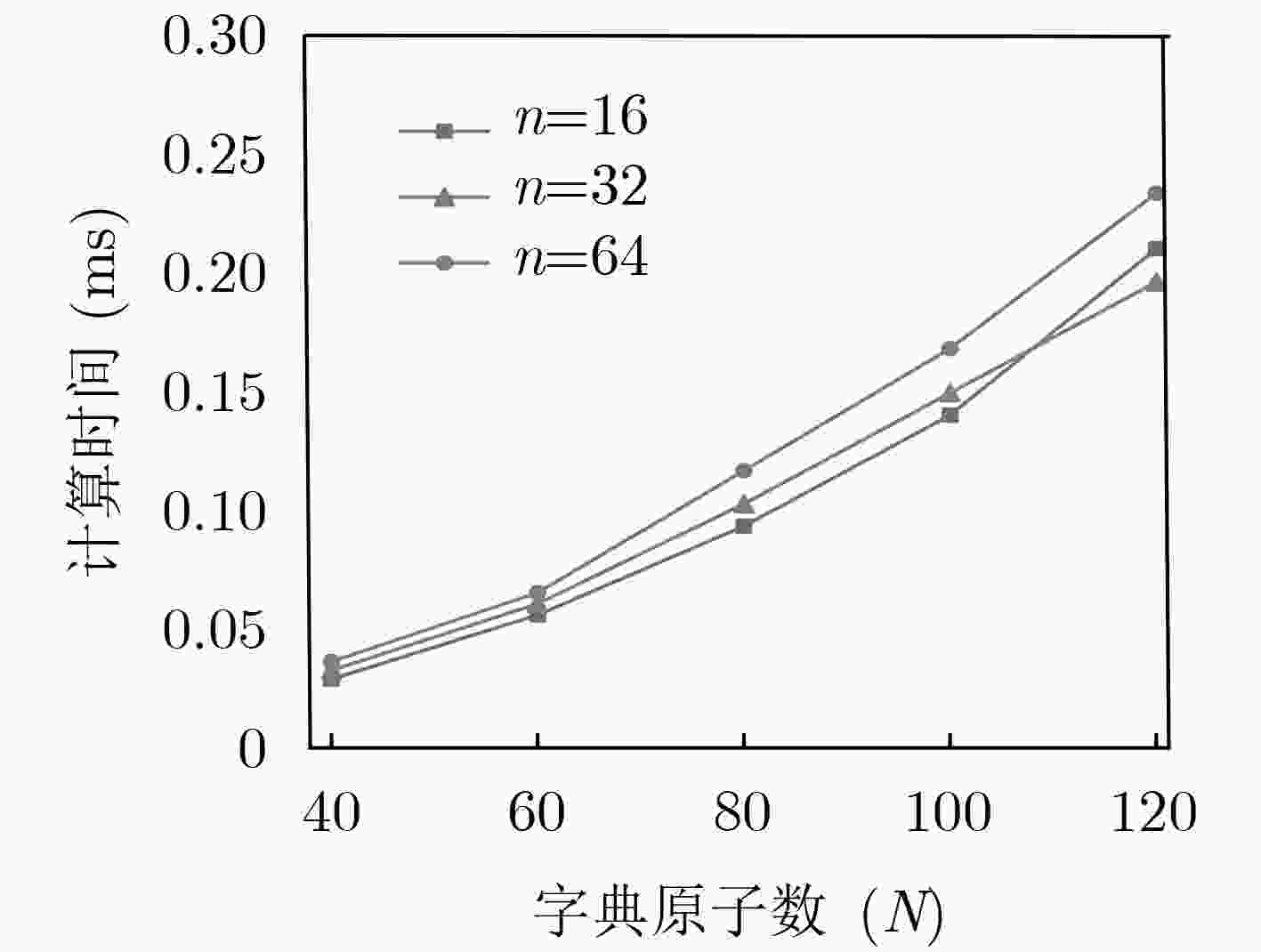
字典原子数(N)	重复交叉验证	分割滑动窗口(n)
		16			32			64
		Se	Sp	Acc	Se	Sp	Acc	Se	Sp	Acc
40	数据集1	97.99	96.63	97.32	98.44	97.95	98.19	98.86	97.75	98.30
	数据集2	97.95	97.42	97.68	98.74	98.15	98.44	98.67	98.43	98.55
	数据集3	98.00	97.99	97.99	98.65	98.51	98.51	98.97	98.30	98.64
	数据集4	97.38	98.44	97.91	98.50	98.67	98.59	98.78	98.57	98.67
	数据集5	98.36	98.34	98.35	98.49	98.55	98.52	98.89	98.57	98.73
	平均	97.94	97.76	97.85	98.56	98.37	98.45	98.83	98.32	98.58
60	数据集1	98.15	96.91	97.53	98.38	98.31	98.34	98.97	96.04	97.51
	数据集2	98.26	97.32	97.79	98.06	98.12	98.09	98.46	94.26	96.36
	数据集3	98.32	97.10	97.71	98.19	98.52	98.36	98.97	98.40	98.68
	数据集4	97.76	98.41	98.09	98.78	98.52	98.65	98.91	98.64	98.78
	数据集5	98.03	98.67	98.35	98.57	98.60	98.58	98.86	98.53	98.69
	平均	98.10	97.68	97.89	98.39	98.41	98.40	98.83	97.17	98.00
80	数据集1	98.15	97.26	97.70	98.52	98.24	98.38	98.97	98.17	98.57
	数据集2	97.99	97.43	97.71	98.81	98.27	98.54	98.97	98.35	98.66
	数据集3	97.98	97.96	97.97	98.86	98.31	98.58	99.00	98.48	98.74
	数据集4	97.39	98.24	97.81	98.73	98.66	98.69	98.93	98.44	98.69
	数据集5	97.60	98.62	98.11	98.65	98.66	98.65	98.88	98.67	98.78
	平均	97.82	97.90	97.86	98.71	98.43	98.57	98.95	98.42	98.69
100	数据集1	98.29	97.29	97.79	98.77	98.23	98.50	99.00	97.01	98.01
	数据集2	98.13	97.72	97.92	98.81	98.09	98.45	98.94	98.56	98.75
	数据集3	97.70	97.72	97.71	97.52	98.51	98.01	98.94	98.80	98.87
	数据集4	97.90	98.38	98.14	98.60	98.72	98.66	98.94	98.80	98.87
	数据集5	98.35	98.47	98.41	98.70	98.68	98.69	98.97	98.63	98.80
	平均	98.07	97.92	97.95	98.48	98.45	98.46	98.96	98.36	98.66
120	数据集1	96.64	94.03	95.33	97.87	95.86	96.86	98.89	97.10	97.99
	数据集2	98.11	93.22	95.66	98.81	97.74	98.28	97.73	97.84	97.79
	数据集3	97.59	97.49	97.04	98.79	98.54	98.66	99.00	97.36	98.18
	数据集4	98.24	98.10	98.17	98.50	98.59	98.54	98.94	98.46	98.70
	数据集5	98.23	98.44	98.34	98.34	98.68	98.51	98.80	98.54	98.67
	平均	97.76	96.26	96.91	98.46	97.88	98.17	98.67	97.86	98.27

下载: 导出CSV

表 2 不同算法分类效果对比(%)

文献	年份	RR间期长度	Se	Sp	Acc
Lian等人^[20]	2011	128	95.89	95.40	–
Huang等人^[18]	2011	128	96.10	98.10	–
Petrėnas等人^[7]	2015	60	97.10	98.30	–
Zhou等人^[19]	2015	128	97.37	98.44	97.99
Cui等人^[8]	2017	150	97.04	97.96	97.78
Andersen等人^[10]	2018	31	98.98	96.95	97.80
本文方法	2019	33	98.71	98.43	98.57

下载: 导出CSV

参考文献(20)

HAQQANI H M, CHAN K H, GREGORY A T, et al. Atrial fibrillation: State of the art in 2017-shifting paradigms in pathogenesis, diagnosis, treatment and prevention[J]. Heart, Lung and Circulation, 2017, 26(9): 867–869. doi: 10.1016/s1443-9506(17)31276-3

DE SISTI A, LECLERCQ J F, HALIMI F, et al. Evaluation of time course and predicting factors of progression of paroxysmal or persistent atrial fibrillation to permanent atrial fibrillation[J]. Pacing and Clinical Electrophysiology, 2014, 37(3): 345–355. doi: 10.1111/pace.12264

ZHOU Xiaolin, DING Hongxia, UNG B, et al. Automatic online detection of atrial fibrillation based on symbolic dynamics and Shannon entropy[J]. BioMedical Engineering OnLine, 2014, 13(1): 18. doi: 10.1186/1475-925X-13-18

SEPULVEDA-SUESCUN J P, MURILLO-ESCOBAR J, URDA-BENITEZ R D, et al. Atrial Fibrillation Detection Through Heart Rate Variability Using a Machine Learning Approach and Poincare Plot Features[M]. TORRES I, BUSTAMANTE J, and SIERRA D A. VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Santander, Colombia. Singapore: Springer Nature Singapore Pte Ltd, 2016: 565–568.

ANDERSEN R S, PEIMANKAR A, and PUTHUSSERYPADY S. A deep learning approach for real-time detection of atrial fibrillation[J]. Expert Systems with Applications, 2019, 115: 465–473. doi: 10.1016/j.eswa.2018.08.011

季虎, 孙即祥, 王春光. 基于小波变换的自适应QRS-T对消P波检测算法[J]. 电子与信息学报, 2007, 29(8): 1868–1871. doi: 10.3724/SP.J.1146.2006.00117

JI Hu, SUN Jixiang, and WANG Chunguang. An adaptive QRS-T cancellation based on wavelet transform for P-wave detection[J]. Journal of Electronics &Information Technology, 2007, 29(8): 1868–1871. doi: 10.3724/SP.J.1146.2006.00117

PETRĖNAS A, SÖRNMO L, LUKOŠEVIČIUS, et al. Detection of occult paroxysmal atrial fibrillation[J]. Medical & Biological Engineering & Computing, 2015, 53(4): 287–297. doi: 10.1007/s11517-014-1234-y

CUI Xingran, CHANG E, YANG Wenhuang, et al. Automated detection of paroxysmal atrial fibrillation using an information-based similarity approach[J]. Entropy, 2017, 19(12): 677. doi: 10.3390/e19120677

XIN Yi and ZHAO Yizhang. Paroxysmal atrial fibrillation recognition based on multi-scale wavelet α-entropy[J]. BioMedical Engineering OnLine, 2017, 16(1): 121. doi: 10.1186/s12938-017-0406-z

TUZEL O, PORIKLI F, and MEER P. Region covariance: A fast descriptor for detection and classification[C]. Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 2006: 589–600.

ZHANG Yingying, YANG Cai, and ZHANG Ping. Two-stage sparse coding of region covariance via Log-Euclidean kernels to detect saliency[J]. Neural Networks, 2017, 89: 84–96. doi: 10.1016/j.neunet.2017.02.012

ARSIGNY V, FILLARD P, PENNEC X, et al. Geometric means in a novel vector space structure on symmetric positive-definite matrices[J]. SIAM Journal on Matrix Analysis and Applications, 2007, 29(1): 328–347. doi: 10.1137/050637996

SCHÖLKOPF B and SMOLA A J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond[M]. Cambridge, USA: MIT Press, 2018: 13. doi: 10.7551/mitpress/4175.003.0018.

LI Peihua, WANG Qilong, ZUO Wangmeng, et al. Log-Euclidean kernels for sparse representation and dictionary learning[C]. 2013 IEEE International Conference on Computer Vision. New York, USA, 2013: 1601–1608. doi: 10.1109/ICCV.2013.202.

GOLDBERGER A L, AMARAl L A N, GLASS L, et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals[J]. Circulation, 2000, 101(23): e215–e220. doi: 10.1161/01.CIR.101.23.e215

HARANDI M T, SANDERSON C, HARTLEY R, et al. Sparse coding and dictionary learning for symmetric positive definite matrices: A kernel approach[C]. The 12th European Conference on Computer Vision, Florence, Italy, 2012: 216-229. doi: 10.1007/978-3-642-33709-3_16.

HUANG Chao, YE Shuming, CHEN Hang, et al. A novel method for detection of the transition between atrial fibrillation and sinus rhythm[J]. IEEE Transactions on Biomedical Engineering, 2011, 58(4): 1113–1119. doi: 10.1109/TBME.2010.2096506

ZHOU Xiaolin, DING Hongxia, WU Wanqing, et al. A real-time atrial fibrillation detection algorithm based on the instantaneous state of heart rate[J]. PLoS One, 2015, 10(9): e0136544. doi: 10.1371/journal.pone.0136544

LIAN Jie, WANG Lian, and MUESSIG D. A simple method to detect atrial fibrillation using RR intervals[J]. The American Journal of Cardiology, 2011, 107(10): 1494–1497. doi: 10.1016/j.amjcard.2011.01.028

LEE J, NAM Y, MCMANUS D D, et al. Time-varying coherence function for atrial fibrillation detection[J]. IEEE Transactions on Biomedical Engineering, 2013, 60(10): 2783–2793. doi: 10.1109/TBME.2013.2264721

施引文献

资源附件(0)

访问统计