Stochastic Average Gradient Descent Contrast Source Inversion Based Nonlinear Inverse Scattering Method for Complex Objects Reconstruction
-
摘要:
采用非线性对比源反演(CSI)算法求解电磁逆散射问题时,在每次迭代过程中都涉及到求解散射场数据关于对比源和总场的微分,即Jacobi矩阵,该矩阵求解导致算法存在计算代价大和收敛速度慢等问题。该文在CSI框架下,采用一种基于随机平均梯度下降的对比源反演算法(SAG-CSI)代替原来的全梯度交替共轭梯度算法来重构介质目标介电常数的空间分布信息。该方法在每次迭代中只需计算随机抽取的部分测量数据在目标函数中的梯度信息,同时目标函数对未抽中的测量数据的梯度信息保持不变,用以上两部分梯度信息共同求解出目标函数的最优值。由模拟数据结果表明,该方法与传统CSI方法在成像精度相比拟的情况下,降低了计算代价并提高算法收敛速度。
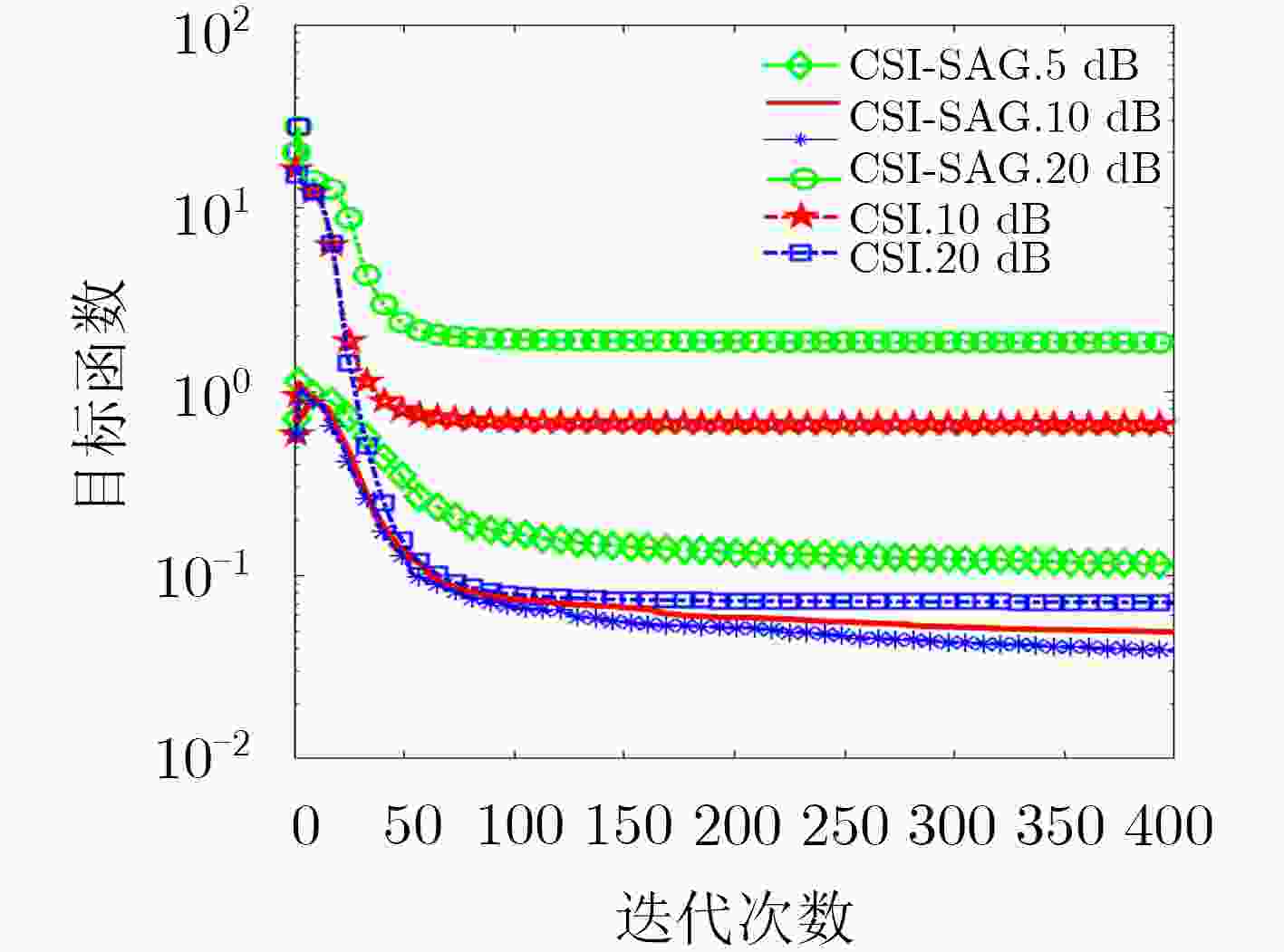
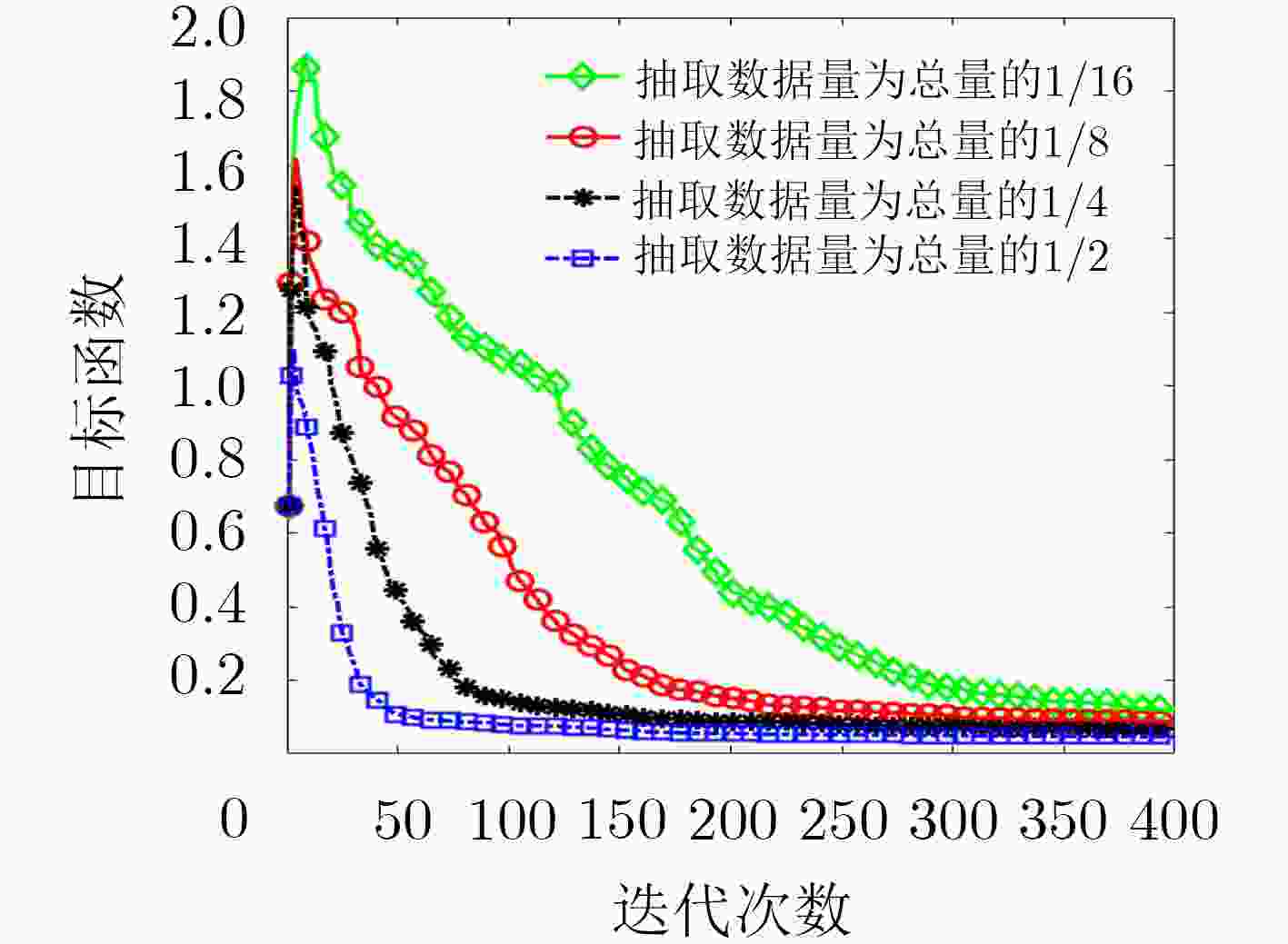
Abstract:When using the nonlinear Contrast Source Inversion (CSI) algorithm to solve the electromagnetic inverse scattering problem, each iteration involves finding the differential of the dissolution radiation field data about the contrast source and the total field, i.e., the Jacobi matrix. the solution of the matrix leads to the problem of large computational cost and slow convergence speed of the algorithm. in this paper, a Contrast Source Inversion algorithm based on Stochastic Average Gradient descent (SAG-CSI) is used instead of the original full gradient alternating Conjugate Gradient algorithm to reconstruct the spatial distribution information of the dielectric constant of the dielectric target under the CSI framework. the method only needs to calculate the gradient information of the randomly selected part of the measurement data in the objective function in each iteration, while the objective function keeps the gradient information of the unscented measurement data, and the optimal value of the objective function is solved together with the above two parts of the gradient information. The simulation results show that the proposed method reduces the computational cost and improves the convergence speed of the algorithm when compared with the traditional CSI method.
-
表 1 SAG-CSI算法
输入:对比源初值:${{{w}}_0}$, 散射场数据:${{{E}}_{{\rm{sca}}}}$, 测量数据的索引:$i \in \left( {1,2, ··· ,N} \right)$, 随机抽取数据的索引:${i_k} \in \left( {1,2, ··· ,N} \right)$。 输出:当目标函数${{{F}}_n}$达到设定误差值$\delta $或最大迭代次数${{{N}}_{{\rm{iter}}}}$时,输出对比度函数:${{{\chi}} _n}$ (1) 计算格林函数${{{G}}_{\rm{D}}}$, ${{{G}}_{\rm{R}}}$ (2) 对比度函数初值${{{\chi}} _0} = 0$, (3) 由前向模型计算得到对比源初值
${ {{w} }_0} = \dfrac{ {\parallel { {{G} }^H_{\rm R} }{ {{E} }_{\rm sca} }{\parallel ^2} } }{ {\parallel { {{G} }_{\rm R} }{ {{G} }^H{\rm R} }{ {{E} }_{\rm sca} }{\parallel ^2} } }{ {{G} }^H_R}{ {{E} }_{\rm sca} }$ (*为共轭转置) (16)(4) $n \leftarrow 0$(n为迭代次数) (5) while ${{{F}}_n}\left( {{w_n}} \right) < {{\delta}} $或${{n}} < {N_{{\rm{iter}}}}$ do 步骤 1 每次迭代随机抽取测量数据的索引:${i_k} = {\rm{randperm}}\left( i \right)$ 步骤 2 将步骤1抽取的测量数据按照进行梯度更新计算(其中$\rho _{n - 1}^{{i_k}}$, $\gamma _{n - 1}^{{i_k}}$和${\chi _{n - 1}}$分别表示随机抽取散射场数据的数据方程误差和场误差以及上次迭代保存的对比度函数)
${{g} }_n^{ {i_k} } = - \frac{ { { {\left( { {{G} }_{\rm{R} }^{ {i_k} } } \right)}^H}\rho _{n - 1}^{ {i_k} } } }{ {\displaystyle\sum\limits_k {\parallel {{E} }_{ {\rm{sca} } }^{ {i_k} }{\parallel ^2} } } } - \frac{ {\gamma _{n - 1}^{ {i_k} } - {{G} }^H_{\rm{D} } { { {{{\chi} } }^* _{n - 1} } } \gamma _{n - 1}^{ {i_k} })} }{ {\displaystyle\sum\limits_k {\parallel { {{\chi} } _{n - 1} }{{E} }_{ {\rm{inc} } }^{ {i_k} }{\parallel ^2} } } }$(*为复共轭) (17)步骤 3 对抽取的散射场数据在目标函数中的梯度值进行更新,其余散射场数据对应的梯度不变(其中${\nabla _{{w_n}}}{{F}}_n^i$表示随机抽取散射场数据在目标函数中关于对比源的更新梯度值,${{g}}_{n - 1}^{{i_k}}$表示上次迭代该散射场数据对应的梯度值,${\overline { { {{g} }_{n - 1} } } }$表示所有散射场数据在目标函数中的梯度矩阵) ${ { { {{\overline{{g} } } }_n} } } ={ { { { {\overline{{g} } } }_{n - 1} } } } - {{g} }_{n - 1}^{ {i_k} } + { {\text{∇} } _{ {w_n} } }{{F} }_n^i$ (18) 将所有测量数据构成的梯度矩阵$\overline{\overline {{{{g}}_n}}} $求和取平均得出当前迭代的梯度${{{g}}_n}$,即搜索方向的反方向。 步骤 4 由步骤3所得的搜索方向和式(15)所求得的搜索步长可计算更新的对比源(上次迭代保存的对比源${{{w}}_{n - 1}}$):${{{w}}_n} \!=\! {{{w}}_{n - 1}} \!-\! {{{\alpha}} _n}{{{g}}_n}$ 步骤 5 更新总场的值:${{E}}_{{\rm{tot}}}^n = E_{{\rm{tot}}}^{n - 1} - {{{\alpha }}_n}{{{G}}_{\rm{D}}}{{{g}}_n}$ 步骤 6 由对比源作为辅助变量公式可知
${ {{\chi} } _n} = \frac{ {\displaystyle\sum\limits_K { { {{w} }_n} ({ { {{{E} } } }_{ {\rm{tot} } }^n})^* } } }{ {\displaystyle\sum\limits_K { {{E} }_{ {\rm{tot} } }^n ({ {{{E} } }_{ {\rm{tot} } }^n})^* } } }$ (*为复共轭,K为抽取样本的总个数) (19)步骤 7 ${{n}} = {{n}} + 1$ (6) end (7) ${{\chi}} = {{{\chi}} _n}$ -
LI Lianlin, WANG Longgang, DING Jun, et al. A probabilistic model for the nonlinear electromagnetic inverse scattering: TM case[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(11): 5984–5991. doi: 10.1109/TAP.2017.2751654 KIM S B, VAN ZYL J J, JOHNSON J T, et al. Surface soil moisture retrieval using the l-band synthetic aperture radar onboard the Soil Moisture Active-Passive satellite and evaluation at core validation sites[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(4): 1897–1914. doi: 10.1109/TGRS.2016.2631126 WANG Longgang, Li Lianlin, DING Jun, et al. A fast patches-based imaging algorithm for 3-D multistatic imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(6): 941–945. doi: 10.1109/LGRS.2017.2688461 VAN DEN BERG P M and KLEINMAN R E. A contrast source inversion method[J]. Inverse Problems, 1997, 13(6): 1607. doi: 10.1088/0266-5611/13/6/013 POLI L, OLIVERI G, and MASSA A. Microwave imaging within the first-order Born approximation by means of the contrast-field Bayesian compressive sensing[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(6): 2865–2879. doi: 10.1109/TAP.2012.2194676 SHEA J D, VAN VEEN B D, and HAGNESS S C. A TSVD analysis of microwave inverse scattering for breast imaging[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(4): 936–945. doi: 10.1109/TBME.2011.2176727 OLIVERI G, ANSELMI N, and MASSA A. Compressive sensing imaging of non-sparse 2D scatterers by a total-variation approach within the Born approximation[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(10): 5157–5170. doi: 10.1109/TAP.2014.2344673 BEVACQUA M T, CROCCO L, DI DONATO L, et al. Non-linear inverse scattering via sparsity regularized contrast source inversion[J]. IEEE Transactions on Computational Imaging, 2017, 3(2): 296–304. doi: 10.1109/TCI.2017.2675708 CHEN Xudong. Subspace-based optimization method for solving inverse-scattering problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 42–49. doi: 10.1109/TGRS.2009.2025122 周辉林, 郑灵辉, 莫仲念, 等. 基于直接采样法和子空间优化法的多介质目标混合逆散射成像方法[J]. 电子与信息学报, 2017, 39(3): 758–762. doi: 10.11999/JEIT160534ZHOU Huilin, ZHENG Linghui, MO Zhongnian, et al. DSM-SOM based hybrid inverse scattering method for multiple dielectric objects reconstruction[J]. Journal of Electronics &Information Technology, 2017, 39(3): 758–762. doi: 10.11999/JEIT160534 SONG Xiaoqian, LI Maokun, YANG Fan, et al. Feasibility study of acoustic imaging for human thorax using an acoustic contrast source inversion algorithm[J]. The Journal of the Acoustical Society of America, 2018, 144(5): 2782–2792. doi: 10.1121/1.5078590 GUO Lei and ABBOSH A M. Microwave imaging of nonsparse domains using Born iterative method with wavelet transform and block sparse Bayesian learning[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(11): 4877–4888. doi: 10.1109/TAP.2015.2473000 YE Xiuzhu and CHEN Xudong. Subspace-based distorted-Born iterative method for solving inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 7224–7232. doi: 10.1109/TAP.2017.2766658 ABUBAKAR A, VAN DEN BERG P M, and KOOIJ B J. A conjugate gradient contrast source technique for 3D profile inversion[J]. IEICE Transactions on Electronics, 2000, E83-C(12): 1864–1874. SCHMIDT M, LE ROUX N, and BACH F. Minimizing finite sums with the stochastic average gradient[J]. Mathematical Programming, 2017, 162(1/2): 83–112. doi: 10.1007/s10107-016-1030-6 DOGNIN P and GOEL V. Combining stochastic average gradient and hessian-free optimization for sequence training of deep neural networks[C]. 2013 IEEE Workshop on Automatic Speech Recognition and Understanding. Olomouc: IEEE, 2013: 321–325. -





 下载:
下载:


 下载:
下载:
