A Robust Trajectory Similarity Measure Method for Classical Trajectory
-
摘要:
针对经典轨迹与实时轨迹之间的大差异性,该文利用最长公共子序列理论,提出一种鲁棒的轨迹相似度量方法。该方法首先利用点到线段之间的距离判断经典轨迹的点与实时轨迹的线段是否一致;然后利用改进的多对1最长公共子序列算法,计算经典轨迹与实时轨迹之间的最长公共子序列长度;最后将最长公共子序列长度与经典轨迹的点数的比值作为经典轨迹与实时轨迹之间的相似度。实验说明该算法的鲁棒性,该算法能够有效解决经典轨迹与实时轨迹之间的大差异轨迹相似度量问题。
-
关键词:
- 轨迹相似度量 /
- 大差异轨迹 /
- 多对1最长公共子序列 /
- 鲁棒计算 /
- 经典轨迹
Abstract:In view of the great difference between classical trajectory and real-time trajectory, a robust trajectory similarity measurement method is proposed based on the longest common subsequence theory. Firstly, the distance between point and line segment is used to judge whether the point of classical trajectory is consistent with the line segment of real-time trajectory. Secondly, the longest common subsequence length between classical trajectory and real-time trajectory is calculated by using the improved multi-to-one longest common subsequence algorithm. Finally, the ratio of the longest common subsequence length to the number of points of the classical trajectory is taken as the similarity between the classical trajectory and the real-time trajectory. Experiments show that the algorithm is robust and can effectively solve the problem of similarity measurement between the classical trajectories and real-time trajectories.
-
ANDRIENKO G, ANDRIENKO N, FUCHS G, et al. Clustering trajectories by relevant parts for air traffic analysis[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(1): 34–44. doi: 10.1109/TVCG.2017.2744322 毛嘉莉, 金澈清, 章志刚, 等. 轨迹大数据异常检测: 研究进展及系统框架[J]. 软件学报, 2017, 28(1): 17–34. doi: 10.13328/j.cnki.jos.005151MAO Jiali, JIN Cheqing, ZHANG Zhigang, et al. Anomaly detection for trajectory big data: Advancements and framework[J]. Journal of Software, 2017, 28(1): 17–34. doi: 10.13328/j.cnki.jos.005151 李保珠, 张林, 董云龙, 等. 基于航迹矢量分级聚类的雷达与电子支援措施抗差关联算法[J]. 电子与信息学报, 2019, 41(6): 1310–1316. doi: 10.11999/JEIT180714LI Baozhu, ZHANG Lin, DONG Yunlong, et al. Anti-bias track association algorithm of radar and electronic support measurements based on track vectors hierarchical clustering[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1310–1316. doi: 10.11999/JEIT180714 陈鸿昶, 徐乾, 黄瑞阳, 等. 一种基于用户轨迹的跨社交网络用户身份识别算法[J]. 电子与信息学报, 2018, 40(11): 2758–2764. doi: 10.11999/JEIT180130CHEN Hongchang, XU Qian, HUANG Ruiyang, et al. User identification across social networks based on user trajectory[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2758–2764. doi: 10.11999/JEIT180130 AGRAWAL R, FALOUTSOS C, and SWAMI A. Efficient similarity search in sequence databases[C]. The 4th International Conference on Foundations of Data Organization and Algorithms, Chicago, USA, 1993: 69–84. KEOGH E and RATANAMAHATANA C A. Exact indexing of dynamic time warping[J]. Knowledge and Information Systems, 2005, 7(3): 358–386. doi: 10.1007/s10115-004-0154-9 GUO Ning, MA Mengyu, XIONG Wei, et al. An efficient query algorithm for trajectory similarity based on Fréchet distance threshold[J]. ISPRS International Journal of Geo-Information, 2017, 6(11): 326. doi: 10.3390/ijgi6110326 魏龙翔, 何小海, 滕奇志, 等. 结合Hausdorff距离和最长公共子序列的轨迹分类[J]. 电子与信息学报, 2013, 35(4): 784–790. doi: 10.3724/SP.J.1146.2012.01078WEI Longxiang, HE Xiaohai, TENG Qizhi, et al. Trajectory classification based on Hausdorff distance and longest common subsequence[J]. Journal of Electronics &Information Technology, 2013, 35(4): 784–790. doi: 10.3724/SP.J.1146.2012.01078 朱进, 胡斌, 邵华. 基于多重运动特征的轨迹相似性度量模型[J]. 武汉大学学报: 信息科学版, 2017, 42(12): 1703–1710. doi: 10.13203/j.whugis20150594ZHU Jin, HU Bin, and SHAO Hua. Trajectory similarity measure based on multiple movement features[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1703–1710. doi: 10.13203/j.whugis20150594 VLACHOS M, KOLLIOS G, and GUNOPULOS D. Discovering similar multidimensional trajectories[C]. The 18th International Conference on Data Engineering, San Jose, USA, 2002: 673–684. doi: 10.1109/ICDE.2002.994784. 刘宇, 王前东. 基于最长公共子序列的非同步相似轨迹判断[J]. 电讯技术, 2017, 57(10): 1165–1170. doi: 10.3969/j.issn.1001-893x.2017.10.011LIU Yu and WANG Qiandong. Computing similar measure between two asynchronous trajectories based on longest common subsequence method[J]. Telecommunication Engineering, 2017, 57(10): 1165–1170. doi: 10.3969/j.issn.1001-893x.2017.10.011 WAGNER R A and FISCHER M J. The string-to-string correction problem[J]. Journal of the ACM, 1974, 21(1): 168–173. doi: 10.1145/321796.321811 CHOONG M Y, ANGELINE L, CHIN R K Y, et al. Modeling of vehicle trajectory clustering based on LCSS for traffic pattern extraction[C]. The 2nd IEEE International Conference on Automatic Control and Intelligent Systems, Kota Kinabalu, Malaysia, 2017: 74–79. doi: 10.1109/I2CACIS.2017.8239036. 王前东. 一种带匹配路径约束的最长公共子序列长度算法[J]. 电子与信息学报, 2017, 39(11): 2615–2619. doi: 10.11999/JEIT170092WANG Qiandong. A matching path constrained longest common subsequence length algorithm[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2615–2619. doi: 10.11999/JEIT170092 WANG Haoxin, ZHONG Jingdong, and ZHANG Defu. A duplicate code checking algorithm for the programming experiment[C]. The 2nd International Conference on Mathematics and Computers in Sciences and in Industry, Sliema, Malta, 2015: 39–42. doi: 10.1109/MCSI.2015.12. YUAN Guan, SUN Penghui, ZHAO Jie, et al. A review of moving object trajectory clustering algorithms[J]. Artificial Intelligence Review, 2017, 47(1): 123–144. doi: 10.1007/s10462-016-9477-7 -






 下载:
下载:
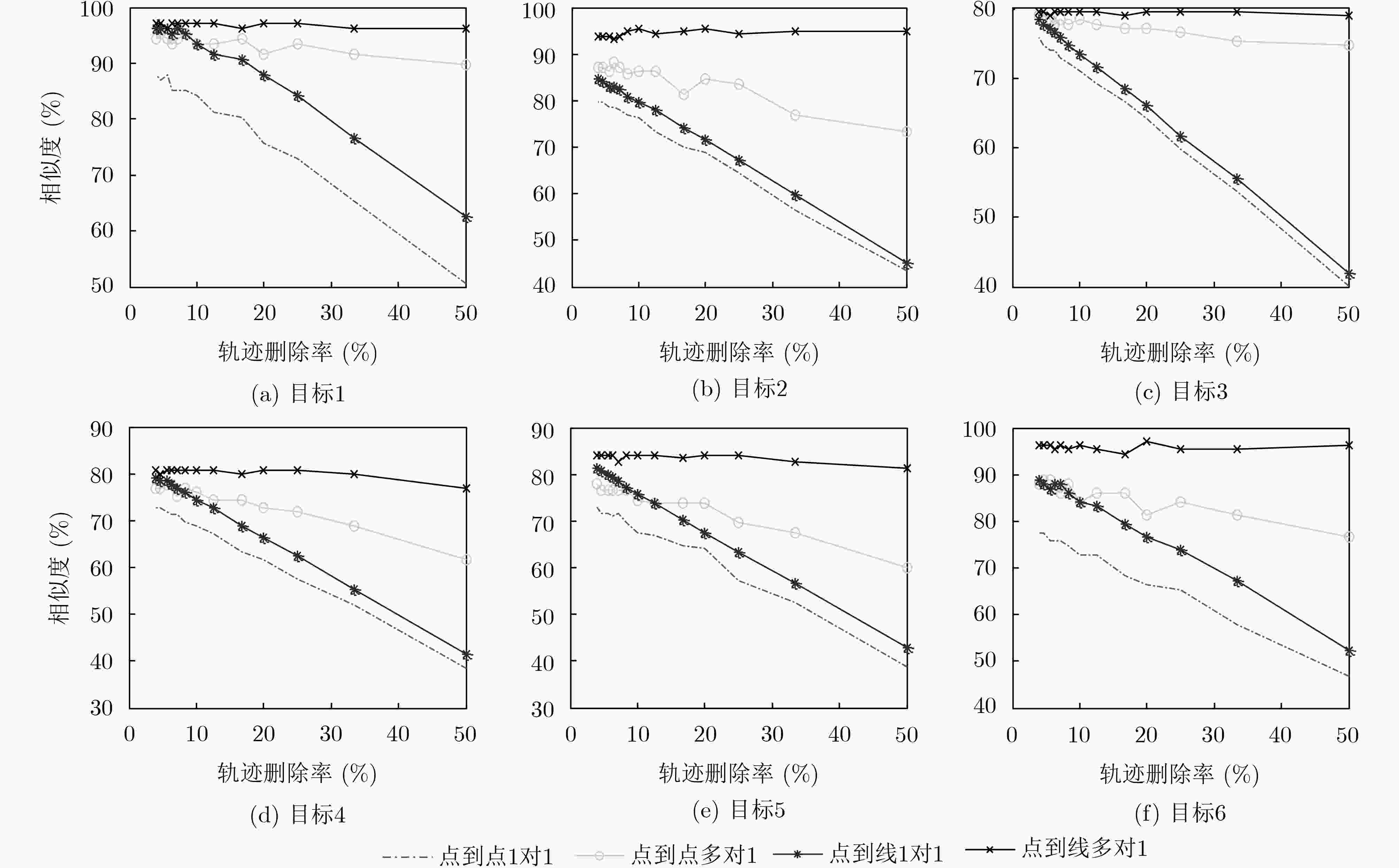
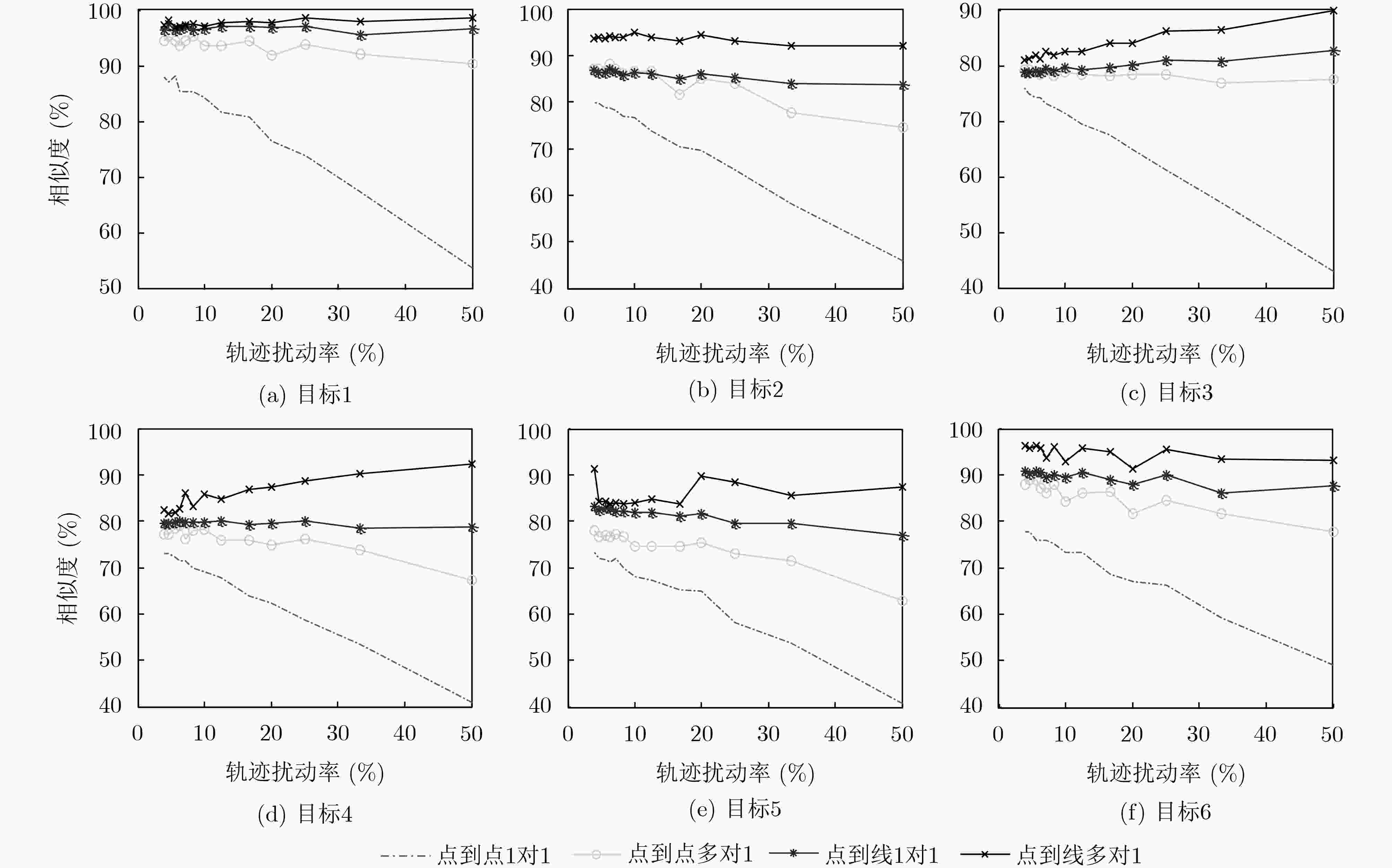


 下载:
下载:
