A Nonparametric Bayesian Dictionary Learning Algorithm with Clustering Structure Similarity
-
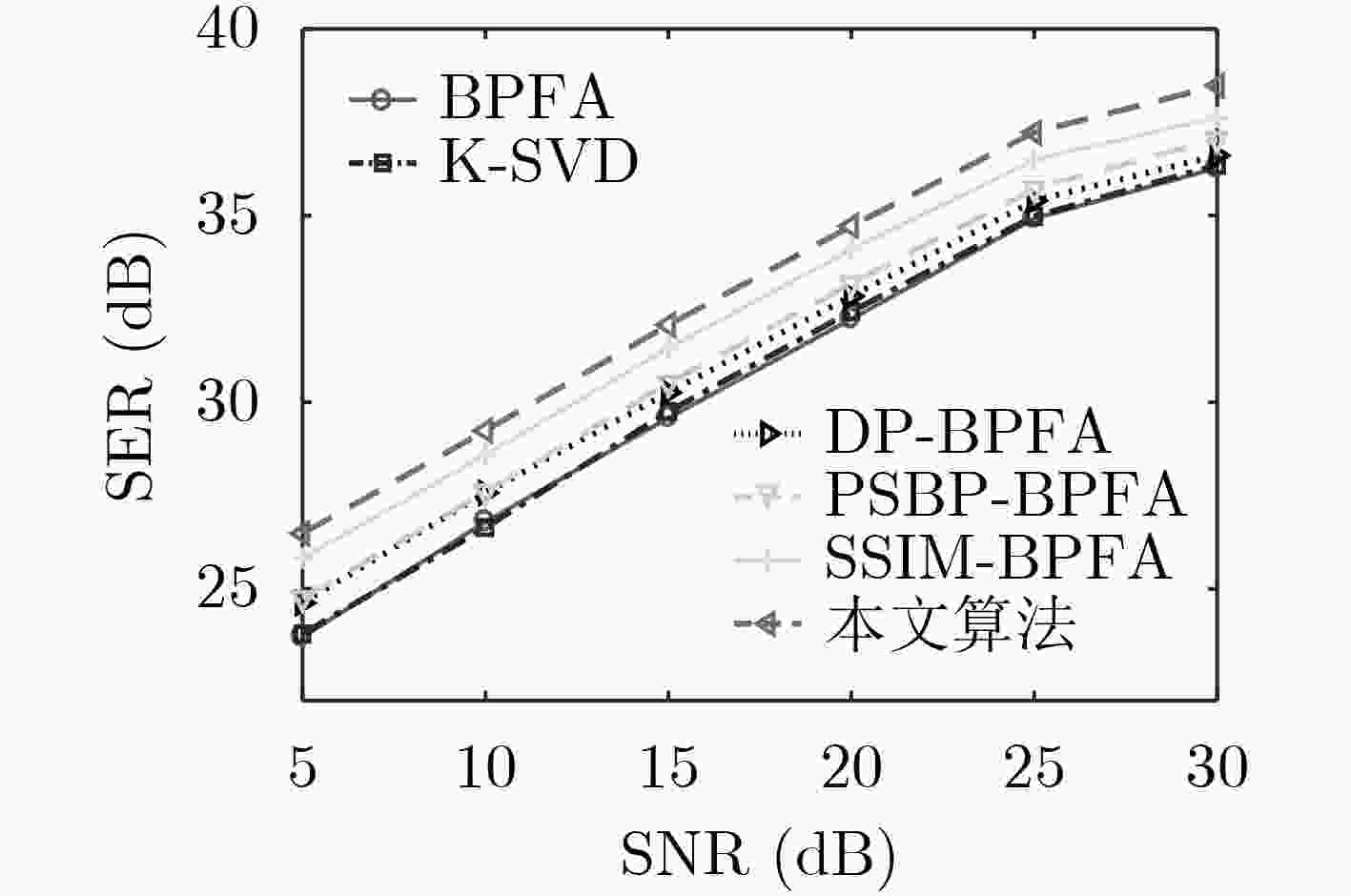
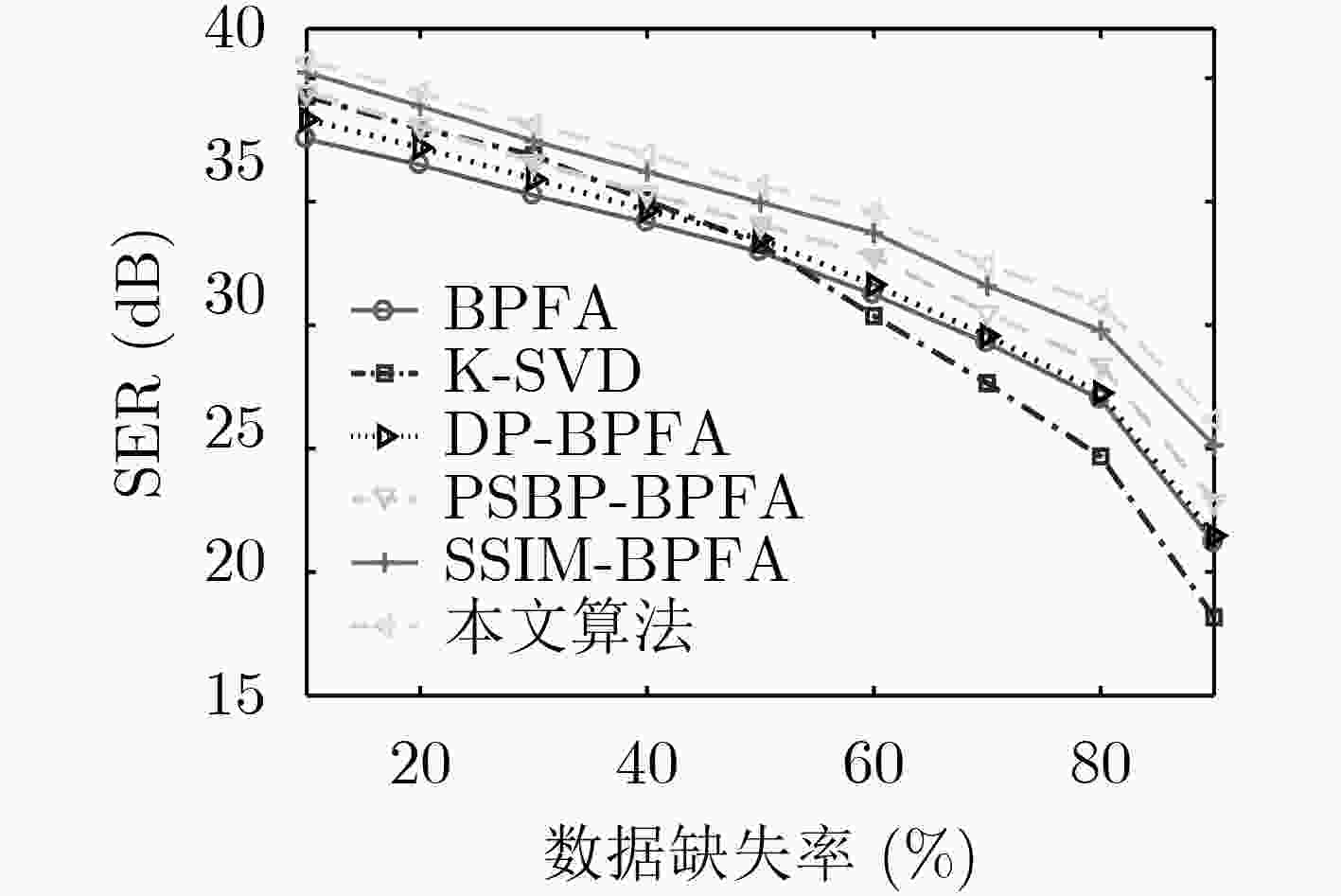
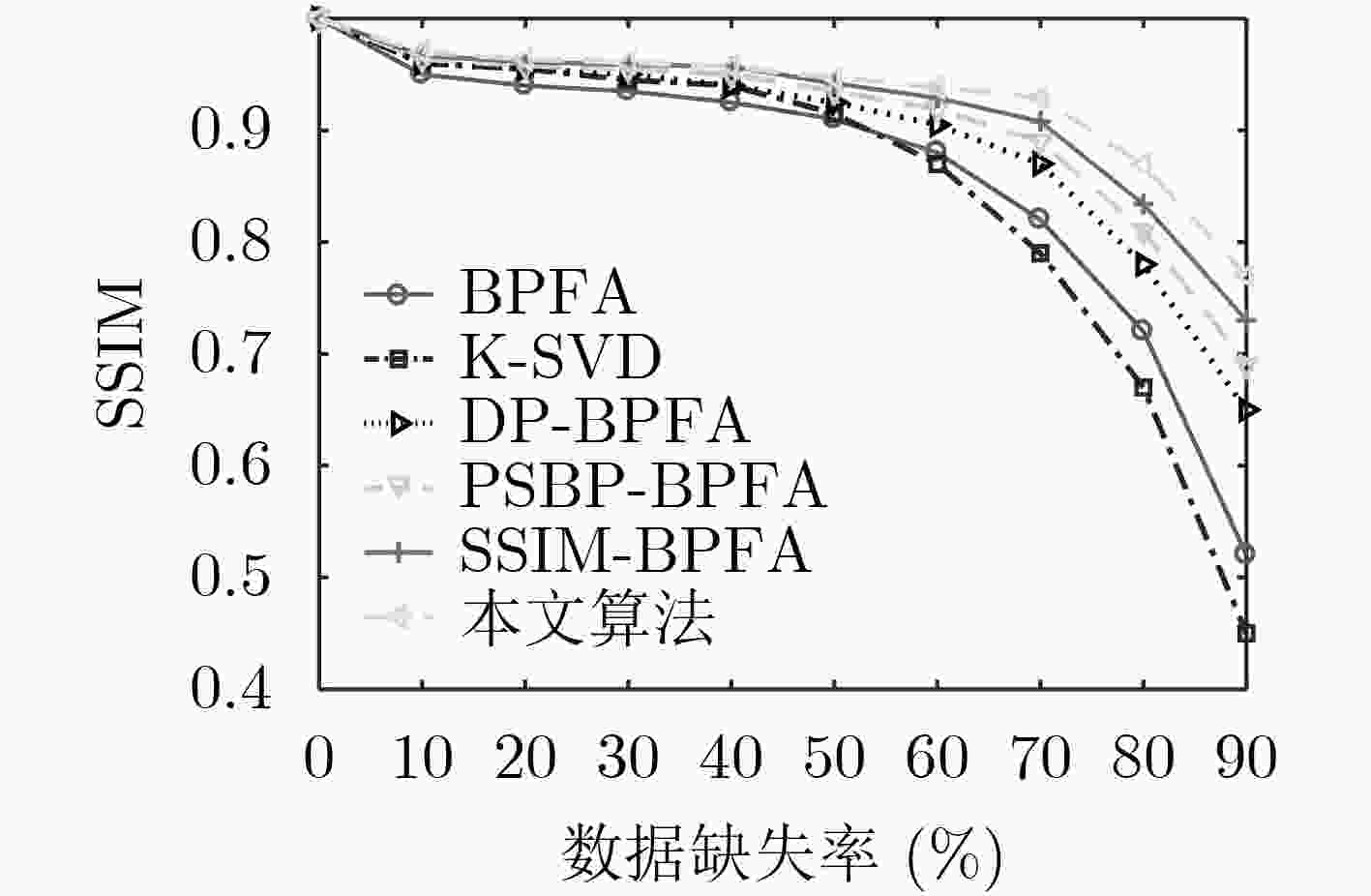
摘要: 利用图像结构信息是字典学习的难点,针对传统非参数贝叶斯算法对图像结构信息利用不充分,以及算法运行效率低下的问题,该文提出一种结构相似性聚类beta过程因子分析(SSC-BPFA)字典学习算法。该算法通过Markov随机场和分层Dirichlet过程实现对图像局部结构相似性和全局聚类差异性的兼顾,利用变分贝叶斯推断完成对概率模型的高效学习,在确保算法收敛性的同时具有聚类的自适应性。实验表明,相比目前非参数贝叶斯字典学习方面的主流算法,该文算法在图像去噪和插值修复应用中具有更高的表示精度、结构相似性测度和运行效率。Abstract: Making use of image structure information is a difficult problem in dictionary learning, the traditional nonparametric Bayesian algorithms lack the ability to make full use of image structure information, and faces problem of inefficiency. To this end, a dictionary learning algorithm called Structure Similarity Clustering-Beta Process Factor Analysis (SSC-BPFA) is proposed in this paper, which completes efficient learning of the probabilistic model via variational Bayesian inference and ensures the convergence and self-adaptability of the algorithm. Image denoising and inpainting experiments show that this algorithm has significant advantages in representation accuracy, structure similarity index and running efficiency compared with the existing nonparametric Bayesian dictionary learning algorithms.
-
Key words:
- Variational Bayesian /
- Markov Random Field (MRF) /
- Dictionary Learning (DL) /
- Denoising /
- Inpainting
-
表 1 模型中隐变量及其变分参数的VB推断更新公式
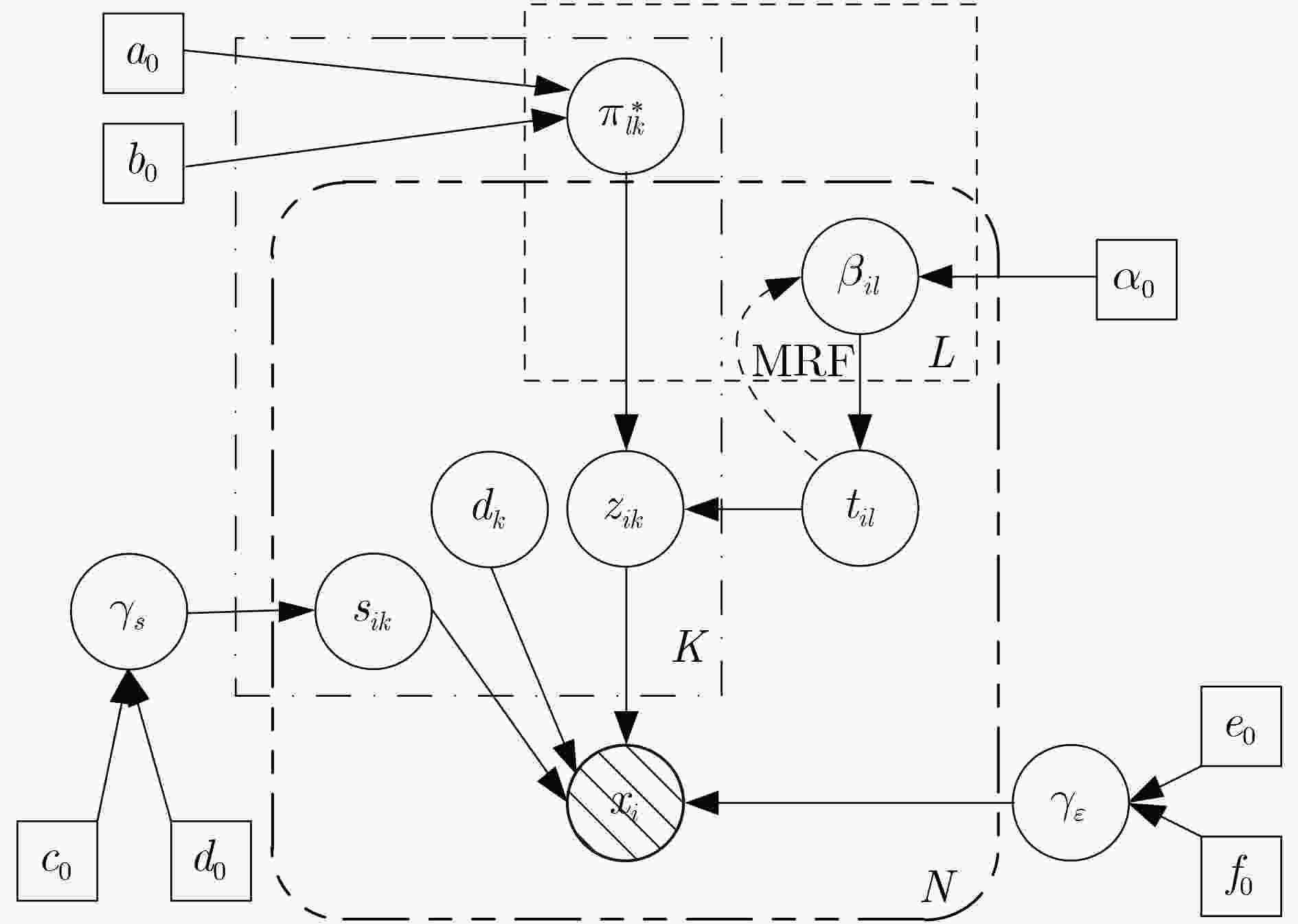
隐变量 变分分布 变分参数的VB推断更新公式 隐变量更新公式 ${{{d}}_k}$ $q\left( {{{{d}}_k}} \right) \propto {\rm{Normal}}\left( {{{{d}}_k}|{{{\tilde { m}}}_k},{{{\tilde { \Lambda }}}_k}} \right)$ ${ {\tilde{ \varLambda } }_k} = P{ {{I} }_P} + \displaystyle\sum\nolimits_{i = 1}^N {\dfrac{ { { {\tilde e}_0} } }{ { { {\tilde f}_0} } }\left( {\tilde \mu _{ik}^2 + \tilde \sigma _{ik}^2} \right){ {\tilde \rho }_{ik} }{ {{I} }_P} }$,
${ {\tilde { m} }_k} = {\tilde { \varLambda } }_k^{ - 1} \cdot \left( {\displaystyle\sum\nolimits_{i = 1}^N {\dfrac{ { { {\tilde e}_0} } }{ { { {\tilde f}_0} } }{ {\tilde \mu }_{ik} }{ {\tilde \rho }_{ik} }{{x} }_i^{ - k} } } \right)$${{{d}}_k} = {{\tilde { m}}_k}$ ${s_{ik}}$ $q\left( {{s_{ik}}} \right) \propto {\rm{Normal}}\left( {{s_{ik}}|{{\tilde \mu }_{ik}},\tilde \sigma _{ik}^2} \right)$ $\tilde \sigma _{ik}^2 = {\left\{ {\dfrac{ { { {\tilde e}_0} } }{ { { {\tilde f}_0} } }{ {\tilde \rho }_{ik} }\left[ { {\tilde { m} }_k^{\rm{T} }{ { {\tilde { m} } }_k} + {\rm{tr(} }{\tilde { \varLambda } }_k^{ - 1}{\rm{)} } } \right] + \dfrac{ { { {\tilde c}_0} } }{ { { {\tilde f}_0} } } } \right\}^{ - 1} }$,
${\tilde \mu _{ik}} = \tilde \sigma _{ik}^2 \cdot \left( {\dfrac{{{{\tilde e}_0}}}{{{{\tilde f}_0}}}{{\tilde \rho }_{ik}}{\tilde { m}}_k^{\rm{T}}{{x}}_i^{ - k}} \right)$${s_{ik}} = {\tilde \mu _{ik}}$ ${z_{ik}}$ $q\left( {{z_{ik}}} \right) \propto {\rm{Bernoulli}}\left( {{z_{ik}}|{{\tilde \rho }_{ik}}} \right)$ ${\tilde \rho _{ik}} = \dfrac{{{\rho _{ik,1}}}}{{{\rho _{ik,1}} + {\rho _{ik,0}}}}$,
${\rho _{ik,0}} = \exp \left\{ \displaystyle\sum\nolimits_{l = 1}^L {{{\tilde \xi }_{il}} \cdot [\psi ({{\tilde b}_{lk}}) - \psi ({{\tilde a}_{lk}} + {{\tilde b}_{lk}})]} \right\} $$\begin{array}{l} {\rho _{ik,1} } = \exp \Bigr\{ - \dfrac{1}{2}\dfrac{ { { {\tilde e}_0} } }{ { { {\tilde f}_0} } }(\tilde \mu _{ik}^2 + \tilde \sigma _{ik}^2)({\tilde { m} }_k^{\rm{T} }{ { {\tilde { m} } }_k} + {\rm{tr} }({\tilde { \varLambda } }_k^{ - 1})) \\\qquad\quad\ + \dfrac{ { { {\tilde e}_0} } }{ { { {\tilde f}_0} } }{ {\tilde \mu }_{ik} }{\tilde { m} }_k^{\rm{T} }{{x} }_i^{ - k} + \displaystyle\sum\nolimits_{l = 1}^L { { {\tilde \xi }_{il} } \cdot [\psi ({ {\tilde a}_{lk} }) - \psi ({ {\tilde a}_{lk} } + { {\tilde b}_{lk} })]} \Bigr\} \end{array}$${z_{ik}} = {\tilde \rho _{ik}}$ $\pi _{lk}^ * $ $q\left( {\pi _{lk}^ * } \right) \propto {\rm{Beta}}\left( {\pi _{lk}^ * |{{\tilde a}_{lk}},{{\tilde b}_{lk}}} \right)$ ${\tilde a_{lk} } = { { {a_0} } / K} + \displaystyle\sum\nolimits_{i = 1}^N { { {\tilde \rho }_{ik} }{ {\tilde \xi }_{il} } }$, ${\tilde b_{lk}} = {{{b_0}(K - 1)} / K} + \displaystyle\sum\nolimits_{i = 1}^N {(1 - {{\tilde \rho }_{ik}}){{\tilde \xi }_{il}}} $ $\pi _{lk}^ * = \dfrac{{{{\tilde a}_{lk}}}}{{{{\tilde a}_{lk}} + {{\tilde b}_{lk}}}}$ ${t_i}$ $q\left( { {t_i} } \right) \propto {\rm{Multi} }\left( { { {\tilde \xi }_{i1} },{ {\tilde \xi }_{i2} },···,{ {\tilde \xi }_{iL} } } \right)$ ${\tilde \xi _{il}} = {{{\xi _{il}}} / {\displaystyle\sum\nolimits_{l' = 1}^L {{\xi _{il'}}} }}$,
$\begin{array}{l} {\xi _{il} } = \exp \Bigr\{ \displaystyle\sum\nolimits_{k = 1}^K { { {\tilde \rho }_{ik} }[\psi ({ {\tilde a}_{lk} }) - \psi ({ {\tilde a}_{lk} } + { {\tilde b}_{lk} })]} \\ \qquad\quad + \displaystyle\sum\nolimits_{k = 1}^K {(1 - { {\tilde \rho }_{ik} })[\psi ({ {\tilde b}_{lk} }) - \psi \left({ {\tilde a}_{lk} } + { {\tilde b}_{lk} }\right)]} \\ \qquad\quad + \psi ({ {\tilde \zeta }_{il} }) - \psi \left(\displaystyle\sum\nolimits_{l' = 1}^L { { {\tilde \zeta }_{il'} } } \right)\Bigr\} \\ \end{array}$${t_i} = \mathop {\arg \max }\limits_l \left\{ {{{\tilde \xi }_{il}},_{}^{}\forall l \in [1,L]} \right\}$ ${\beta _{il}}$ $q\left( {\{ {\beta _{il} }\} _{l = 1}^L} \right) \propto {\rm{Diri} }\left( { { {\tilde \lambda }_{i1} },{ {\tilde \lambda }_{i2} },···,{ {\tilde \lambda }_{iL} } } \right)$ ${\tilde \lambda _{il}} = {\tilde \xi _{il}} + {\alpha _0}{G_{il}}$ ${\beta _{il}} = {{{{\tilde \lambda }_{il}}} / {\displaystyle\sum\nolimits_{l' = 1}^L {{{\tilde \lambda }_{il'}}} }}$ ${\gamma _s}$ $q\left( {{\gamma _s}} \right) \propto {\rm{Gamma}}\left( {{\gamma _s}|{{\tilde c}_0},{{\tilde d}_0}} \right)$ ${\tilde c_0} = {c_0} + \dfrac{1}{2}NK$, ${\tilde d_0} = {d_0} + \dfrac{1}{2}\displaystyle\sum\nolimits_{i = 1}^N {\displaystyle\sum\nolimits_{k = 1}^K {\left( {\tilde \mu _{ik}^2 + \tilde \sigma _{ik}^2} \right)} } $ ${\gamma _s} = {{{{\tilde c}_0}} / {{{\tilde d}_0}}}$ ${\gamma _\varepsilon }$ $q\left( {{\gamma _\varepsilon }} \right) \propto {\rm{Gamma}}\left( {{\gamma _\varepsilon }|{{\tilde e}_0},{{\tilde f}_0}} \right)$ ${\tilde e_0} = {e_0} + \dfrac{1}{2}NP$, ${\tilde f_0} = {f_0} + \dfrac{1}{2}\displaystyle\sum\nolimits_{i = 1}^N {\left\| {{{{x}}_i} - {\hat{ D}}\left( {{{{\hat{ s}}}_i} \odot {{{\hat{ z}}}_i}} \right)} \right\|} $ ${\gamma _\varepsilon } = {{{{\tilde e}_0}} / {{{\tilde f}_0}}}$ 算法1 SSC-BPFA算法 输入:训练数据样本集$\left\{ {{{{x}}_i}} \right\}_{i = 1}^N$ 输出:字典${{D}}$、权重$\left\{ {{{{s}}_i}} \right\}_{i = 1}^N$、稀疏模式指示向量$\left\{ {{{{z}}_i}} \right\}_{i = 1}^N$及聚类标签$\left\{ {{t_i}} \right\}_{i = 1}^N$ 步骤 1 设置收敛阈值$\tau $和迭代次数上限${\rm{it}}{{\rm{r}}_{\max }}$,初始化原子数目$K$与聚类数目$L$,通过K-均值算法对数据样本进行初始聚类; 步骤 2 按照式(1)—式(15)完成NPB-DL的概率建模; 步骤 3 初始化隐变量集${{\varTheta } }$和变分参数集${{{ H}}}$,计算${\hat{ X}} = {{D}}\left( {{{S}} \odot {{Z}}} \right)$,令迭代索引${\rm{itr}}$=1; 步骤 4 按照表1的VB推断公式对${{\varTheta } }$和${{{ H}}}$进行更新,计算${{\hat{ X}}^{{\rm{new}}}} = {{D}}\left( {{{S}} \odot {{Z}}} \right)$;
步骤 5 令${\rm{itr}}$值增加1,删除${{D}}$中未使用的原子并更新$K$的值,计算$r = {{\left\| {{{{\hat{ X}}}^{{\rm{new}}}} - {\hat{ X}}} \right\|_{\rm{F}}^2} / {\left\| {{\hat{ X}}} \right\|_{\rm{F}}^2}}$,若$r < \tau $或${\rm{itr}} \ge {\rm{it}}{{\rm{r}}_{\max }}$,删除所含样本
占全部样本数量比例低于${10^{ - 3}}$的聚类,将被删聚类内的样本分配到剩余聚类中${\tilde \xi _{il}}$最大的那个聚类中,进入步骤6,否则跳回步骤4;步骤 6 固定${t_i}$和${\beta _{il}}$及其变分参数的估计结果,将${{{d}}_k}$, ${s_{ik}}$, ${z_{ik}}$, $\pi _{lk}^ * $, ${\gamma _s}$和${\gamma _\varepsilon }$这6个隐变量及其对应的变分参数继续进行迭代优化更新,直至
重新达到收敛. -
XUAN Junyu, LU Jie, ZHANG Guangquan, et al. Doubly nonparametric sparse nonnegative matrix factorization based on dependent Indian buffet processes[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(5): 1835–1849. doi: 10.1109/TNNLS.2017.2676817 LI Shaoyang, TAO Xiaoming, and LU Jianhua. Variational Bayesian inference for nonparametric signal compressive sensing on structured manifolds[C]. 2017 IEEE International Conference on Communications, Paris, France, 2017. doi: 10.1109/ICC.2017.7996389. DANG H P and CHAINAIS P. Indian buffet process dictionary learning: Algorithms and applications to image processing[J]. International Journal of Approximate Reasoning, 2017, 83: 1–20. doi: 10.1016/j.ijar.2016.12.010 SERRA J G, TESTA M, MOLINA R, et al. Bayesian K-SVD using fast variational inference[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3344–3359. doi: 10.1109/TIP.2017.2681436 NGUYEN V, PHUNG D, BUI H, et al. Discriminative Bayesian nonparametric clustering[C]. The 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 2017. doi: 10.24963/ijcai.2017/355. HUYNH V and PHUNG D. Streaming clustering with Bayesian nonparametric models[J]. Neurocomputing, 2017, 258: 52–62. doi: 10.1016/j.neucom.2017.02.078 AHARON M, ELAD M, and BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. doi: 10.1109/TSP.2006.881199 ELAD M and AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(2): 3736–3745. doi: 10.1109/TIP.2006.881969 ZHOU Mingyuan, CHEN Haojun, PAISLEY J, et al. Nonparametric Bayesian dictionary learning for analysis of noisy and incomplete images[J]. IEEE Transactions on Image Processing, 2012, 21(1): 130–144. doi: 10.1109/TIP.2011.2160072 ZHOU Mingyuan, PAISLEY J, and CARIN L. Nonparametric learning of dictionaries for sparse representation of sensor signals[C]. The 3rd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Aruba, Netherlands, 2009. doi: 10.1109/CAMSAP.2009.5413290. PAISLEY J, ZHOU Mingyuan, SAPIRO G, et al. Nonparametric image interpolation and dictionary learning using spatially-dependent Dirichlet and beta process priors[C]. 2010 IEEE International Conference on Image Processing, Hong Kong, China, 2010. doi: 10.1109/ICIP.2010.5653350. JU Fujiao, SUN Yanfeng, GAO Junbin, et al. Nonparametric tensor dictionary learning with beta process priors[J]. Neurocomputing, 2016, 218: 120–130. doi: 10.1016/j.neucom.2016.08.064 KNOWLES D and GHAHRAMANI Z. Infinite sparse factor analysis and infinite independent components analysis[C]. The 7th International Conference on Independent Component Analysis and Signal Separation, London, UK, 2007: 381–388. doi: 10.1007/978-3-540-74494-8_48. ZHANG Linlin, GUINDANI M, VERSACE F, et al. A spatio-temporal nonparametric Bayesian variable selection model of fMRI data for clustering correlated time courses[J]. NeuroImage, 2014, 95: 162–175. doi: 10.1016/j.neuroimage.2014.03.024 AKHTAR N and MIAN A. Nonparametric coupled Bayesian dictionary and classifier learning for hyperspectral classification[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(9): 4038–4050. doi: 10.1109/TNNLS.2017.2742528 POLATKAN G, ZHOU Mingyuan, CARIN L, et al. A Bayesian nonparametric approach to image super-resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(2): 346–358. doi: 10.1109/TPAMI.2014.2321404 董道广, 芮国胜, 田文飚, 等. 基于结构相似性的非参数贝叶斯字典学习算法[J]. 通信学报, 2019, 40(1): 43–50. doi: 10.11959/j.issn.1000-436x.2019015DONG Daoguang, RUI Guosheng, TIAN Wenbiao, et al. Nonparametric Bayesian dictionary learning algorithm based on structural similarity[J]. Journal on Communications, 2019, 40(1): 43–50. doi: 10.11959/j.issn.1000-436x.2019015 BISHOP C M. Pattern Recognition and Machine Learning (Information Science and Statistics)[M]. New York: Springer, 2006: 461–522. -





 下载:
下载:





 下载:
下载:
