A Preferential Recovery Method of Interdependent Networks under Load
-
摘要:
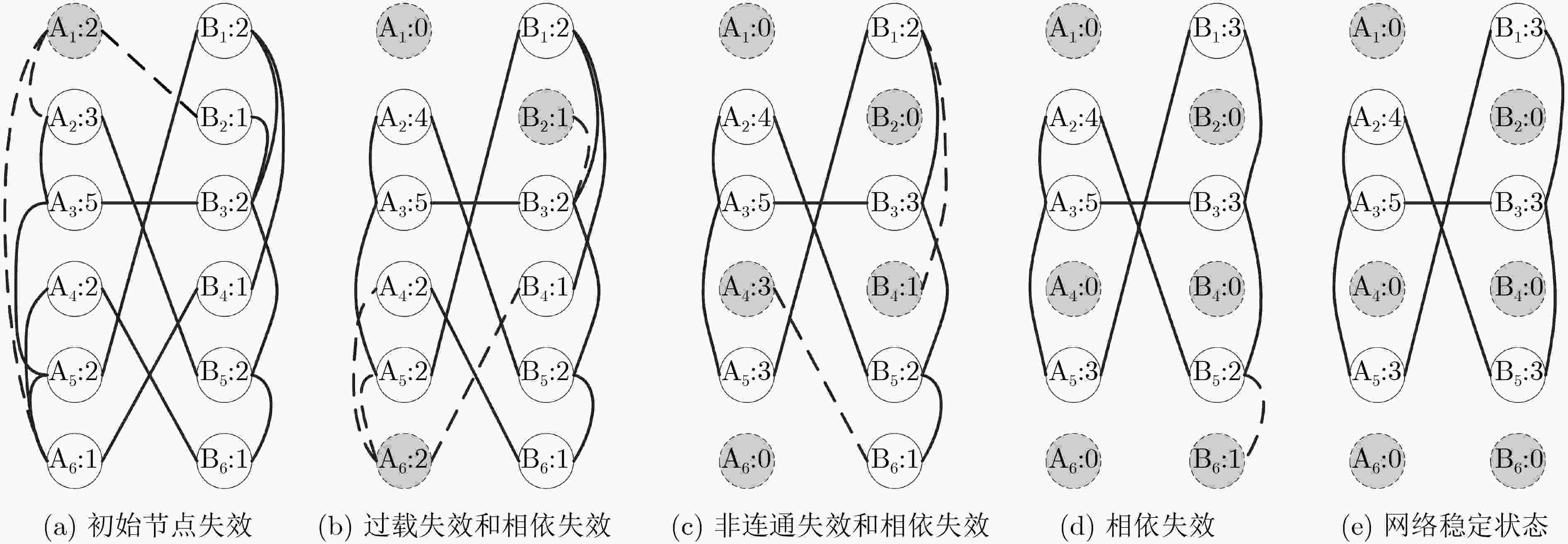
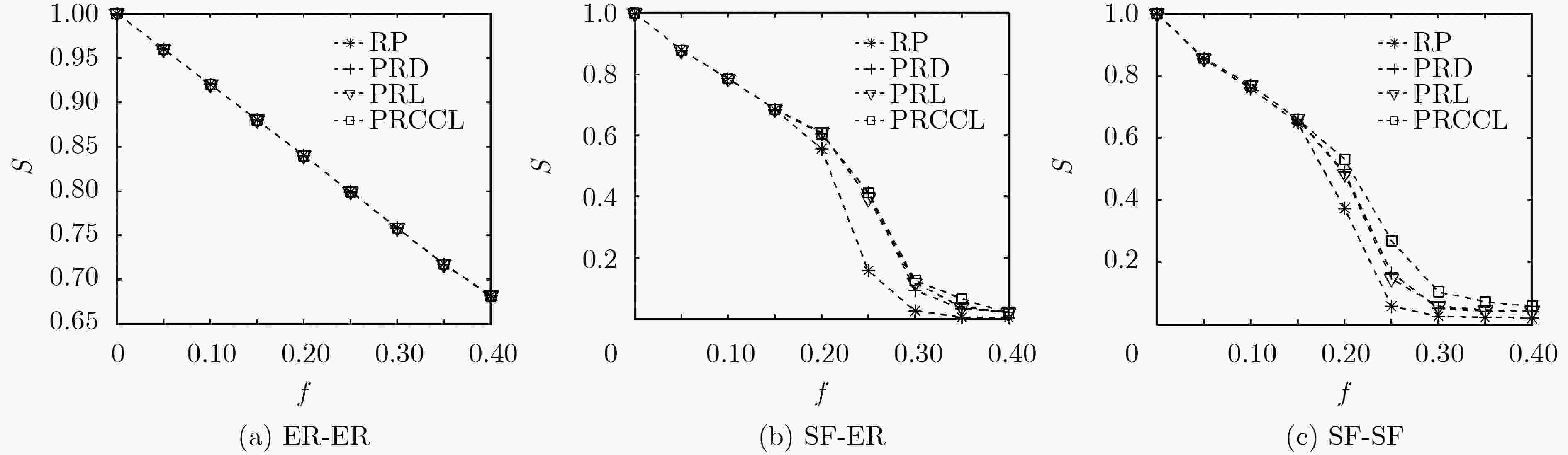
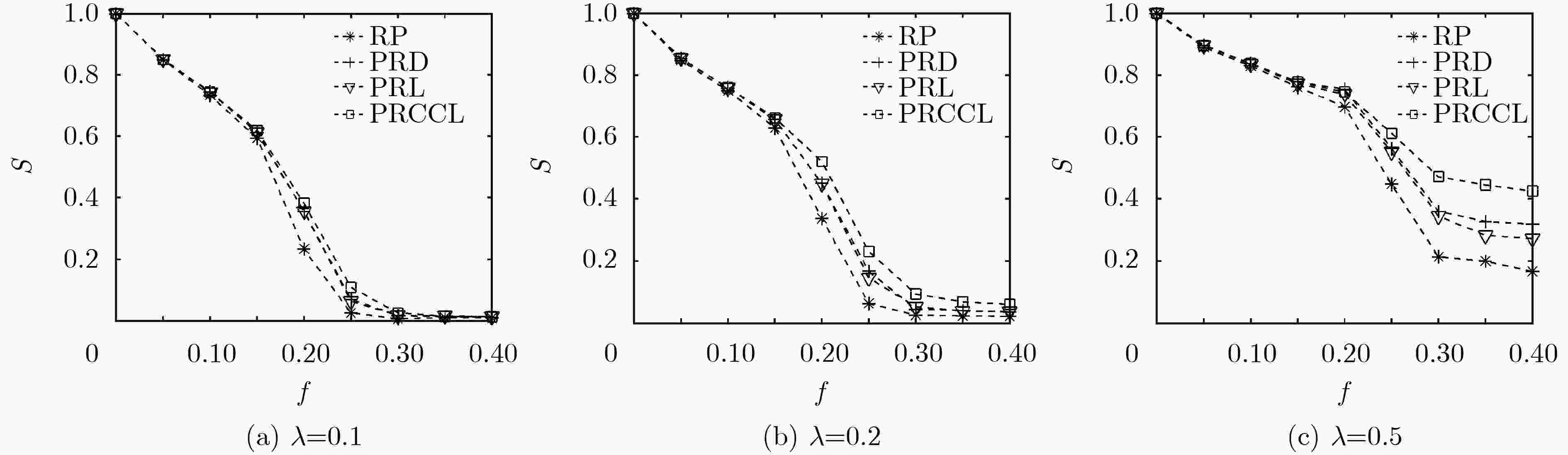
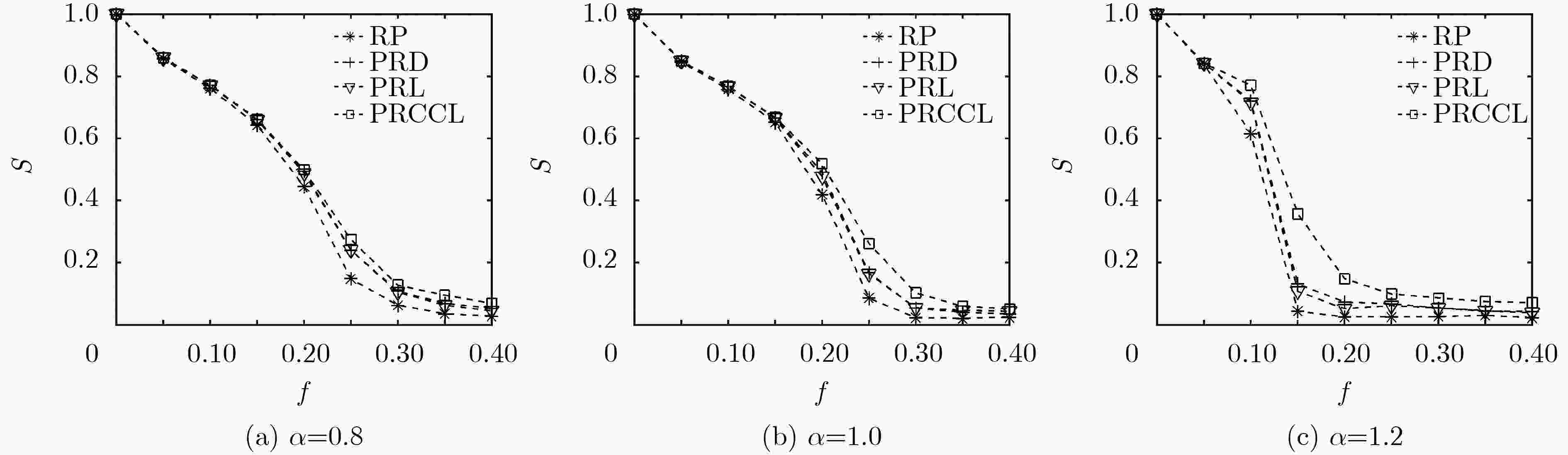
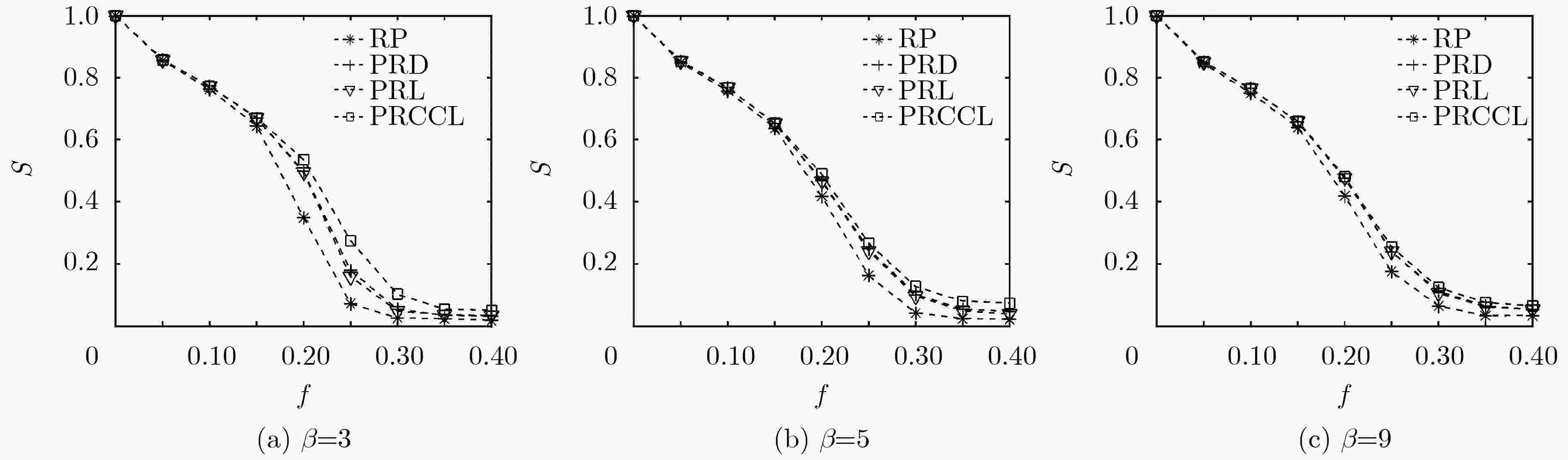
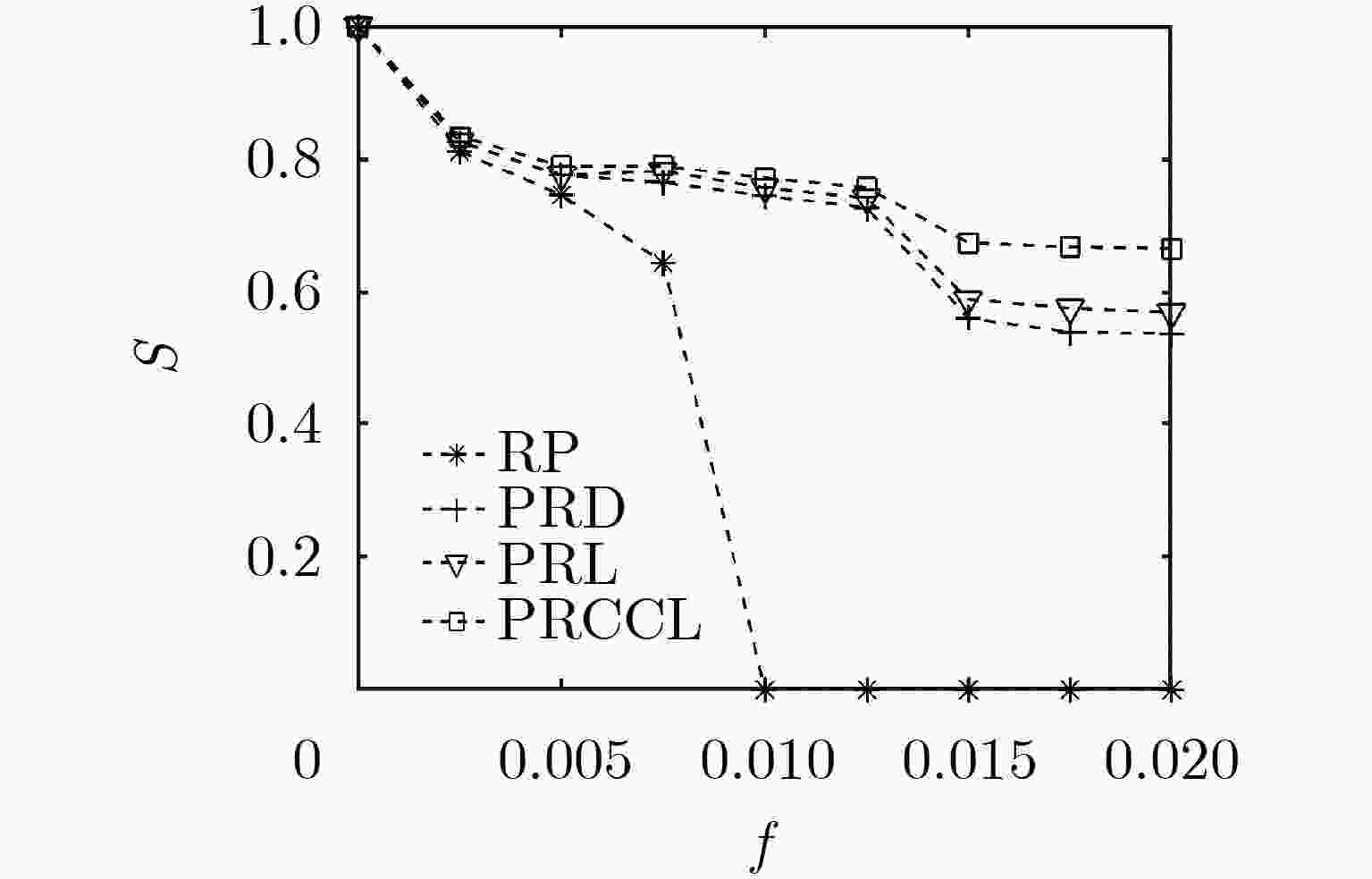
优选节点实施恢复是控制相依网络级联失效的有效措施。针对以往恢复模型未考虑节点负载的情况,该文首先分析了包含依赖失效和过载失效的级联失效过程,构建了负载作用下相依网络恢复模型。然后,基于共同边界节点的结构和动力学属性,提出一种基于容量和连接边的择优恢复(PRCCL)方法。实验结果表明,在无标度相依网络中,PRCCL方法恢复效果明显好于基准方法,恢复时间更短,恢复后的网络具有更高的平均度和鲁棒性;在Power网和Internet网构成的相依网络中,PRCCL方法恢复效果同样优于基准方法;PRCCL方法的优势与恢复比例、负载控制参数成正比,与容忍系数成反比。实验结果验证了PRCCL方法的有效性,对于现实中相依网络恢复工作具有科学指导价值。
Abstract:Optimal node recovery is an effective measure to control cascading failure of interdependent networks. In view of the fact that the previous recovery model does not consider the node load, this paper analyzes first the cascading failure process including dependent failure and overload failure, and constructs the recovery model of interdependent network under load. Then, considering the structure and dynamic properties of the mutual boundary nodes, a Preferential Recovery method based on Capacity and Connectivity Link (PRCCL) is proposed. Experiment results show that in scale-free independent networks, the recovery effect of PRCCL is better than benchmark methods, the recovery time is shorter, and the recovered networks have higher average degree and robustness. In the independent network composed of Power grid and Internet network, the recovery effect of PRCCL method is also better than the benchmark methods. The advantages of PRCCL are proportional to the recovery ratio, load control parameters and inversely proportional to the tolerance coefficient. The experimental results verify the validity of the PRCCL method, which has scientific guidance value for the recovery of interdependent networks in reality.
-
Key words:
- Interdependent networks /
- Network recovery /
- Cascading failure /
- Load effect
-
表 1 SF-ER和SF-SF相依网络中4种方法迭代次数(NOI)对比
SF-ER SF-SF f 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 RR 2.00 2.00 2.15 4.09 10.99 10.44 10.13 8.73 3.04 3.10 3.61 9.68 15.10 15.59 15.75 16.94 PRD 2.00 2.00 2.14 4.02 9.67 7.29 6.17 5.56 3.03 3.06 3.22 5.94 11.69 11.85 12.25 12.13 PRL 2.00 2.00 2.14 4.16 9.82 8.47 6.83 6.39 3.03 3.06 3.24 6.4 12.06 12.01 12.09 12.48 PRCCL 2.00 2.00 2.14 3.99 9.61 7.27 5.81 5.12 3.03 3.07 3.20 4.98 9.12 9.42 10.07 11.06 表 2 4种方法恢复后网络平均度和网络负载对比
恢复网络平均度 恢复网络负载 f 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 RR 3.99 3.28 2.83 1.91 0.75 0.60 0.50 0.48 1186.5 1162.3 1102.8 654.8 121.8 42.9 51.9 124.3 PRD 4.68 4.23 3.91 3.46 1.79 1.08 1.02 0.90 1185.2 1161.4 1107.5 835.6 261.8 56.4 78.2 131.4 PRL 4.66 4.18 3.87 3.38 1.85 1.09 1.09 0.99 1185.2 1161.5 1108.4 817.8 268.3 62.0 83.8 142.4 PRCCL 4.69 4.22 4.00 4.02 2.78 1.56 1.12 1.10 1185.3 1162.0 1111.6 948.9 410.5 149.5 92.0 144.3 -
D’AGOSTINO G and SCALA A. Networks of Networks: The Last Frontier of Complexity[M]. Cham: Springer, 2014: 3–36. CHEN Zhenhao, WU Jiajing, XIA Yongxiang, et al. Robustness of interdependent power grids and communication networks: A complex network perspective[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(1): 115–119. doi: 10.1109/TCSII.2017.2705758 BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025–1028. doi: 10.1038/nature08932 ZIO E. Challenges in the vulnerability and risk analysis of critical infrastructures[J]. Reliability Engineering & System Safety, 2016, 152: 137–150. doi: 10.1016/j.ress.2016.02.009 SHEKHTMAN L M, DANZIGER M M, and HAVLIN S. Recent advances on failure and recovery in networks of networks[J]. Chaos, Solitons & Fractals, 2016, 90: 28–36. doi: 10.1016/j.chaos.2016.02.002 SCHNEIDER C M, YAZDANI N, ARAÚJO N A M, et al. Towards designing robust coupled networks[J]. Scientific Reports, 2013, 3(1): 1969. doi: 10.1038/srep01969 WANG Xingyuan, ZHOU Wenjie, LI Rui, et al. Improving robustness of interdependent networks by a new coupling strategy[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 492: 1075–1080. doi: 10.1016/j.physa.2017.11.037 PARSHANI R, ROZENBLAT C, IETRI D, et al. Inter-similarity between coupled networks[J]. EPL (Europhysics Letters) , 2010, 92(6): 68002. doi: 10.1209/0295-5075/92/68002 WANG Junde, LAO Songyang, RUAN Yirun, et al. Research on the robustness of interdependent networks under localized attack[J]. Applied Sciences, 2017, 7(6): 597. doi: 10.3390/app7060597 HU Yanqing, ZHOU Dong, ZHANG Rui, et al. Percolation of interdependent networks with intersimilarity[J]. Physical Review E, 2013, 88(5): 052805. doi: 10.1103/PhysRevE.88.052805 WANG Shuai and LIU Jing. Designing comprehensively robust networks against intentional attacks and cascading failures[J]. Information Sciences, 2019, 478: 125–140. doi: 10.1016/j.ins.2018.11.005 MAJDANDZIC A, PODOBNIK B, BULDYREV S V, et al. Spontaneous recovery in dynamical networks[J]. Nature Physics, 2014, 10(1): 34–38. doi: 10.1038/NPHYS2819 MAJDANDZIC A, BRAUNSTEIN L A, CURME C, et al. Multiple tipping points and optimal repairing in interacting networks[J]. Nature Communications, 2016, 7(1): 10850. doi: 10.1038/ncomms10850 DI MURO M A, LA ROCCA C E, STANLEY H E, et al. Recovery of interdependent networks[J]. Scientific Reports, 2016, 6(1): 22834. doi: 10.1038/srep22834 HE Xian and CHA E J. Modeling the damage and recovery of interdependent critical infrastructure systems from natural hazards[J]. Reliability Engineering & System Safety, 2018, 177: 162–175. doi: 10.1016/j.ress.2018.04.029 ZHONG Jilong, ZHANG Fengming, YANG Shunkun, et al. Restoration of interdependent network against cascading overload failure[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 512: 884–891. doi: 10.1016/j.physa.2018.09.130 吴佳键, 龚凯, 王聪, 等. 相依网络上基于相连边的择优恢复算法[J]. 物理学报, 2018, 67(8): 088901. doi: 10.7498/aps.67.20172526WU Jiajian, GONG Kai, WANG Cong, et al. Enhancing resilience of interdependent networks against cascading failures under preferential recovery strategies[J]. Acta Physica Sinica, 2018, 67(8): 088901. doi: 10.7498/aps.67.20172526 MOTTER A E and LAI Yingcheng. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102. doi: 10.1103/PhysRevE.66.065102 GAO Jiazi, YIN Yongfeng, FIONDELLA L, et al. Recovery of coupled networks after cascading failures[J]. Journal of Systems Engineering and Electronics, 2018, 29(3): 650–657. doi: 10.21629/JSEE.2018.03.22 CHEN Duanbing, LÜ Linyuan, SHANG Mingsheng, et al. Identifying influential nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(4): 1777–1787. doi: 10.1016/j.physa.2011.09.017 WATTS D J and STROGATZ S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440–442. doi: 10.1038/30918 NEWMAN M. University of Oregon route views archive project[EB/OL]. http://routeviews.org/, 2006. -





 下载:
下载:



 下载:
下载:
