A Survey of Orbital Angular Momentum in Wireless Communication
-
摘要:
电磁涡旋因携带轨道角动量而具有高维可调制自由度,被引入无线通信中以提升频谱效率和抗干扰能力。该文首先介绍了轨道角动量和电磁涡旋的基本原理与特性;然后比较了电磁涡旋的产生方法,给出了超表面产生轨道角动量的工作原理,综述了基于超表面的轨道角动量产生方法和研究现状;总结了轨道角动量的传输性能、接收与检测方法、复用与解复用性能;最后讨论了未来在应用无线通信轨道角动量时需要解决的关键问题。
Abstract:Electromagnetic vortices are introduced into wireless communication to improve spectral efficiency and anti-interference capability. In this paper, the basic principle and characteristics of Orbital Angular Momentum (OAM) and electromagnetic eddy are introduced firstly. The principle of generating Orbital Angular Momentum from supersurface is given, and the methods and research status of generating orbital angular momentum based on supersurface are summarized. The transmission performance, receiving and detecting method, multiplexing and demultiplexing performance of orbital angular momentum are summarized. Finally, the key problems to be solved in the future application of wireless communication orbital angular momentum are discussed.
-
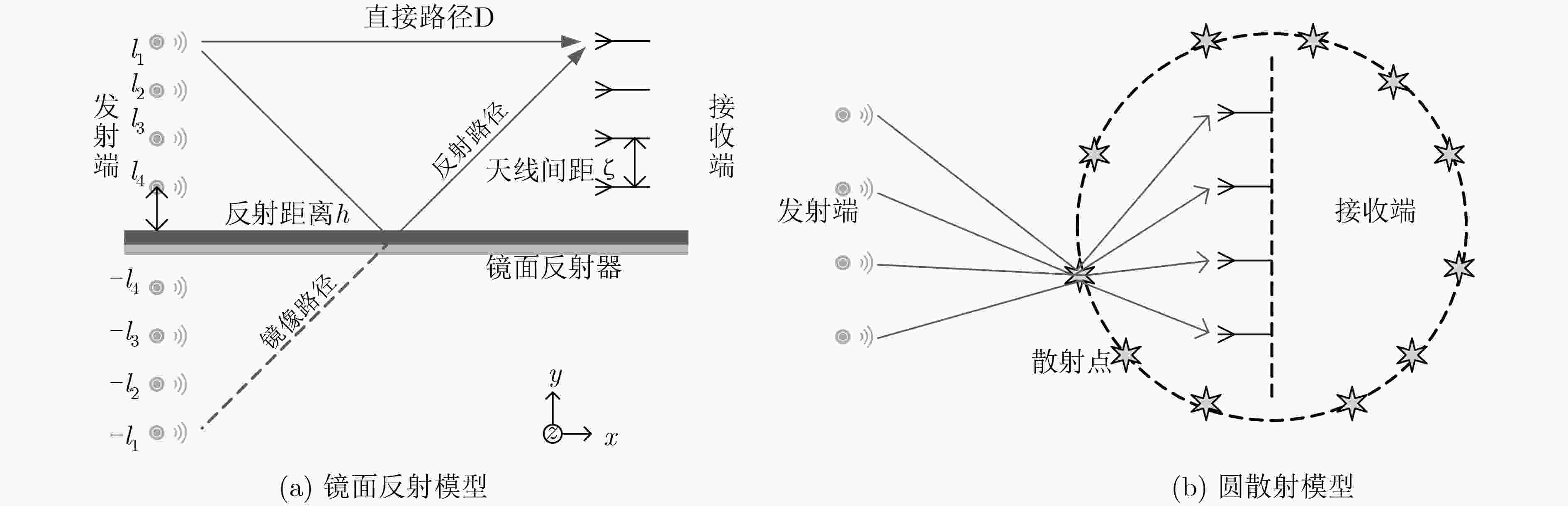
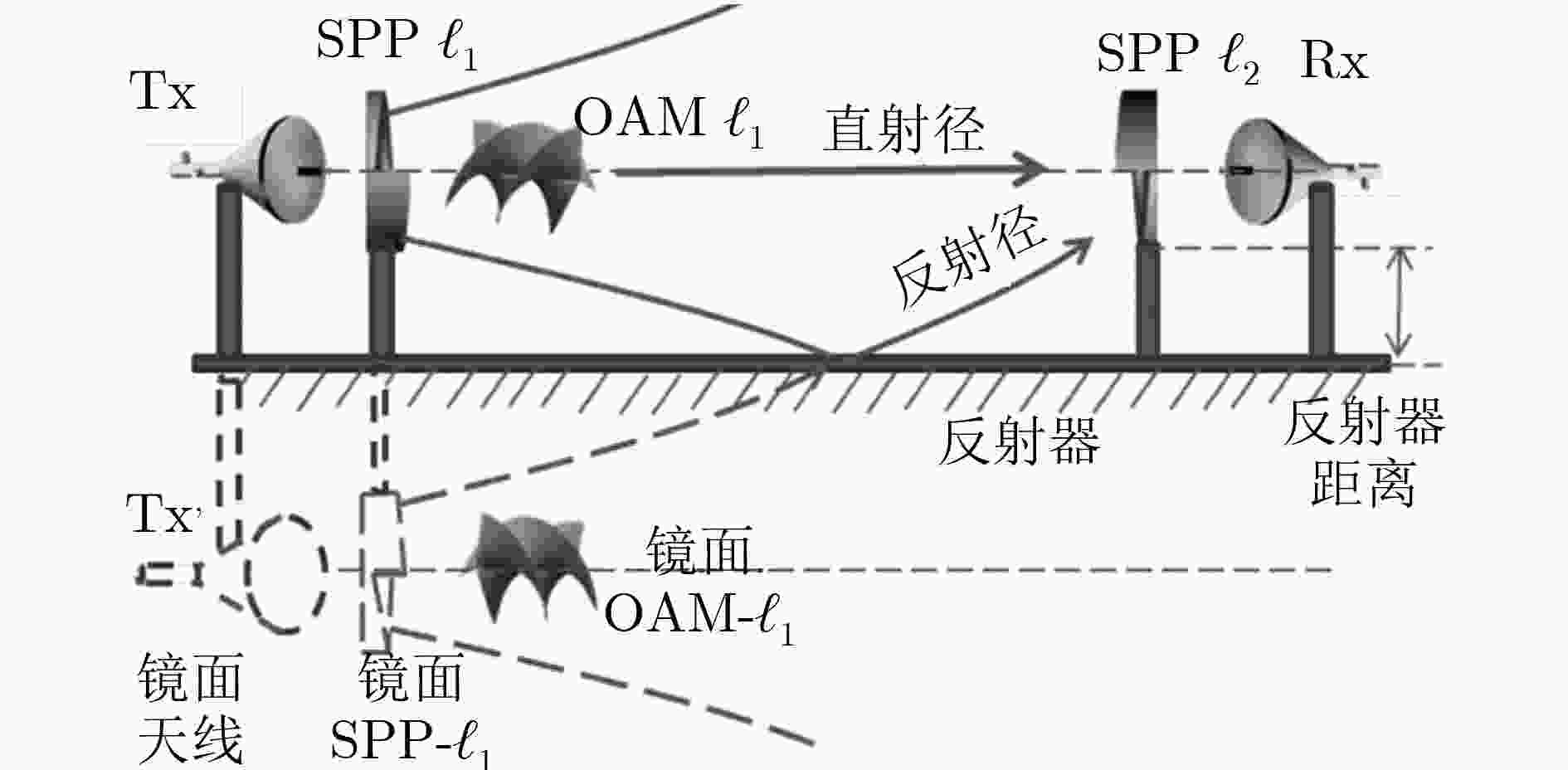
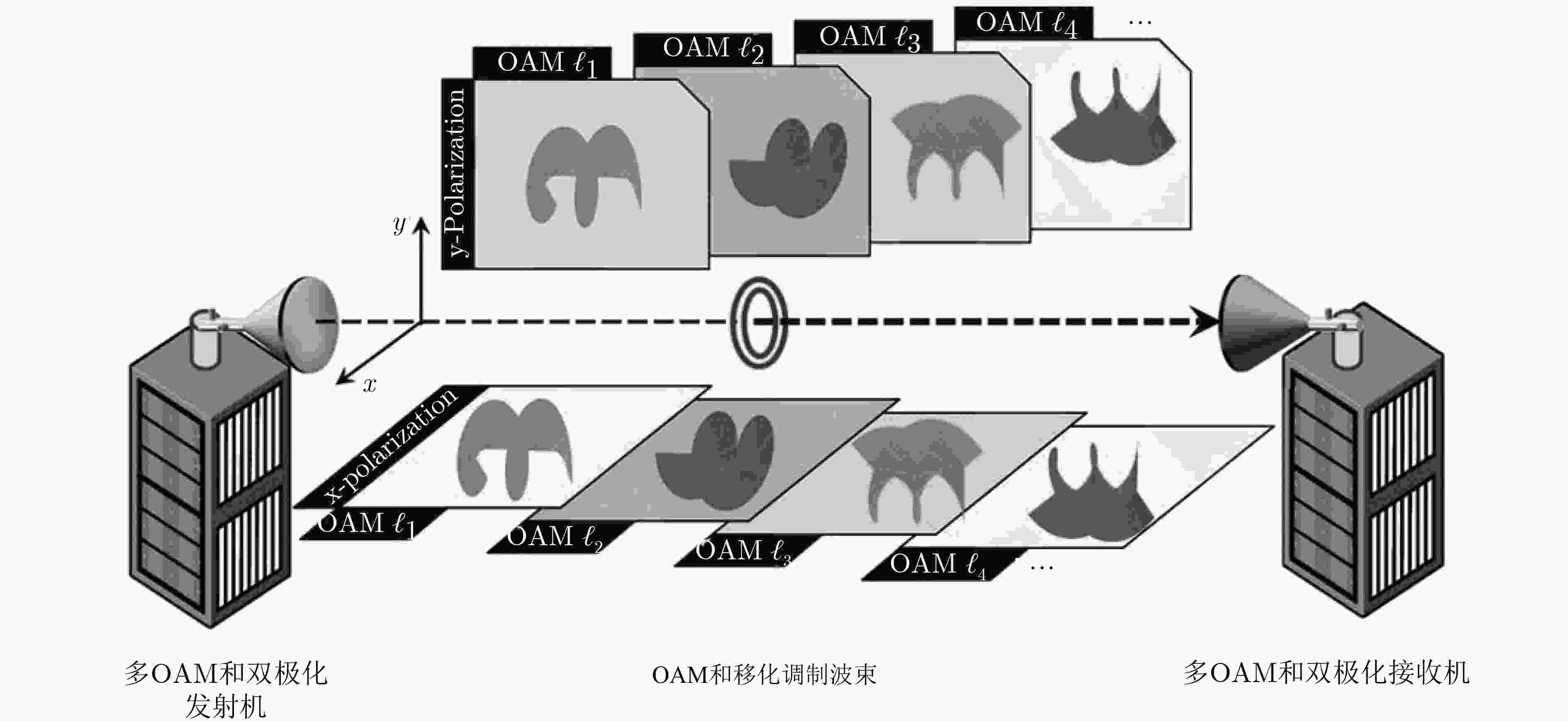
图 6 OAM多径效应镜面反射模型示意图[47]
表 1 电磁涡旋特性
特性 基本原理 潜在应用 正交性 任意两个整数阶模态的OAM波束互相正交,构成无穷维希尔伯特空间 提升系统频谱效率 发散性 随着距离和OAM阶数的增加,OAM波束发散程度加剧 – 稳定性 OAM的相位结构与传输距离无关[26];当拓扑电荷为整数时相位奇点处场强为零,并且随着传播距离增加,中心对称的场强分布保持稳定。 实现长距离传输 反射性 OAM涡旋波束经过镜面反射只改变旋转方向不影响波前相位结构 有利于分析多径效应
对传输系统的影响安全性 受到角度限制和横向偏移的影响,在传输过程中对信号的抽样检测存在不确定性[9],可有效防止信息被窃取。 更高编码强度,实现高容量高保密性通信[27] 多维量子纠缠 单光子或纠缠光子可用于量子信息处理,非整数模态OAM模态可以分解为整数OAM模态的线性叠加;纠缠的量子态不可分离[28]。 表 2 典型OAM产生方法与分类
产生方式 生成原理 典型代表 优缺点 应用 透射光栅结构 利用干涉条纹产生的交叉错位结果得到的叉形光栅生成相位全息图,结合计算机仿真数据制作相位全息面。 空间光调制器 成本低、转换速度快、可工作在任意频率、系统复杂度较低;但是仅能实现单模态和非纯模态的生成、器件实现较复杂。 可用于毫米波频段产生OAM波束,通过空间复用提高频谱效率。 透射螺旋结构 波束透过厚度$h$随中心旋转方位角$\phi $比例变化的相位板,产生相位差随厚度变化的透射电磁波。 单阶梯型螺旋相位板多阶梯型螺旋相位板多孔型螺旋相位板 成本低、转换效率高、系统复杂度较低;但是仅能在单点频率上实现单模态转换,并且器件转换过程较复杂。 可用于实现高容量、高频谱效率的毫米波和太赫兹通信。 透射反射面 波束入射到非平面螺旋结构的不同区域,导致波束相邻部分存在相对延迟。 阶梯型反射面
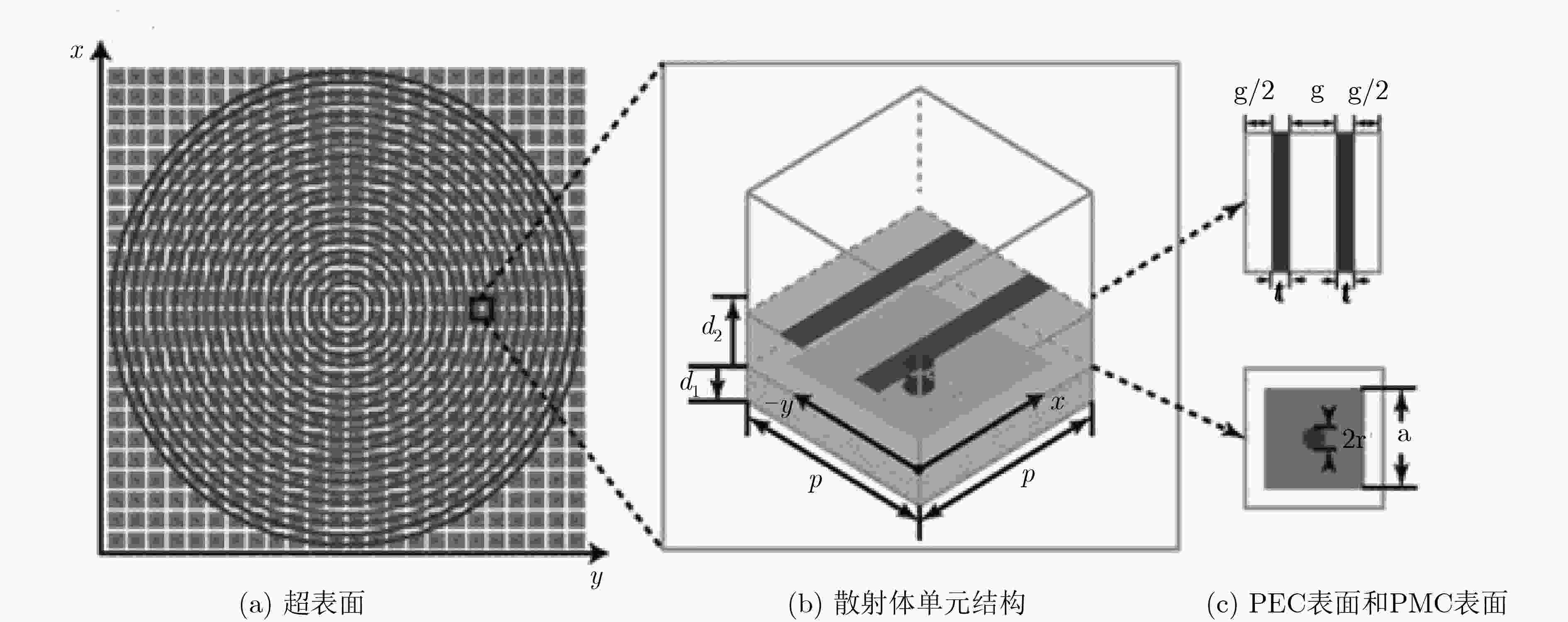
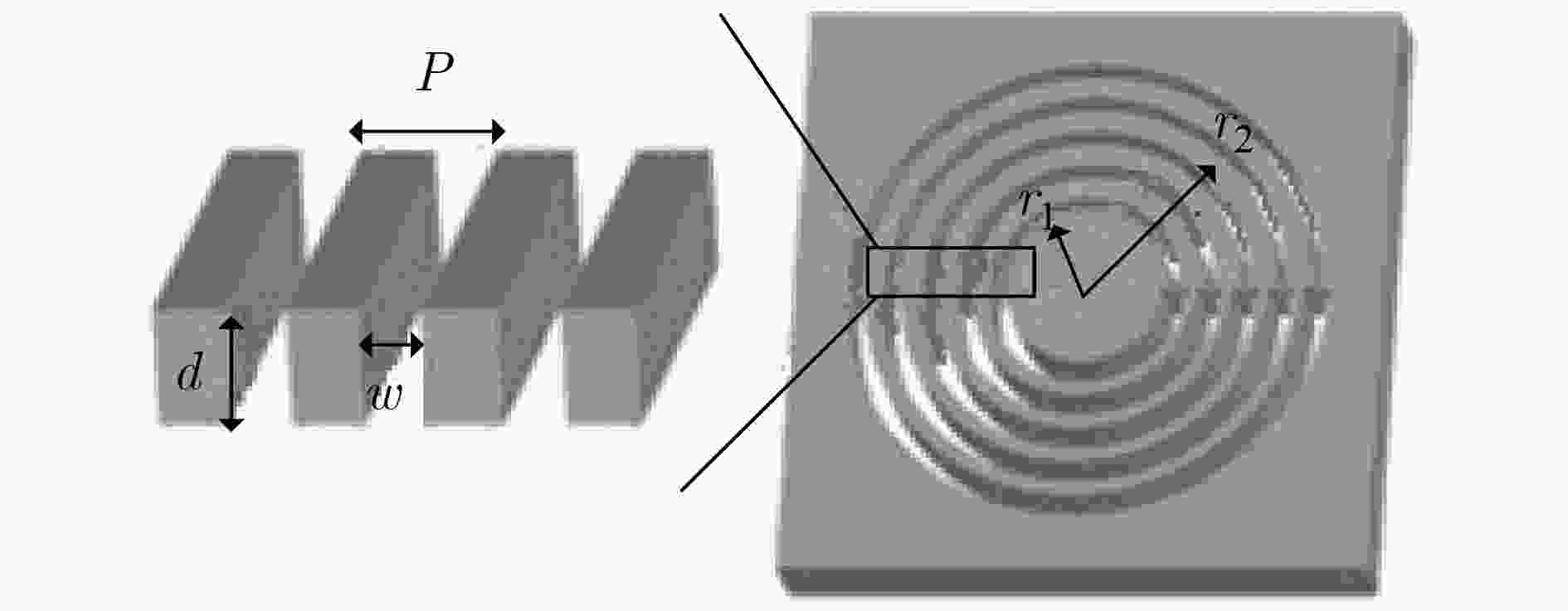
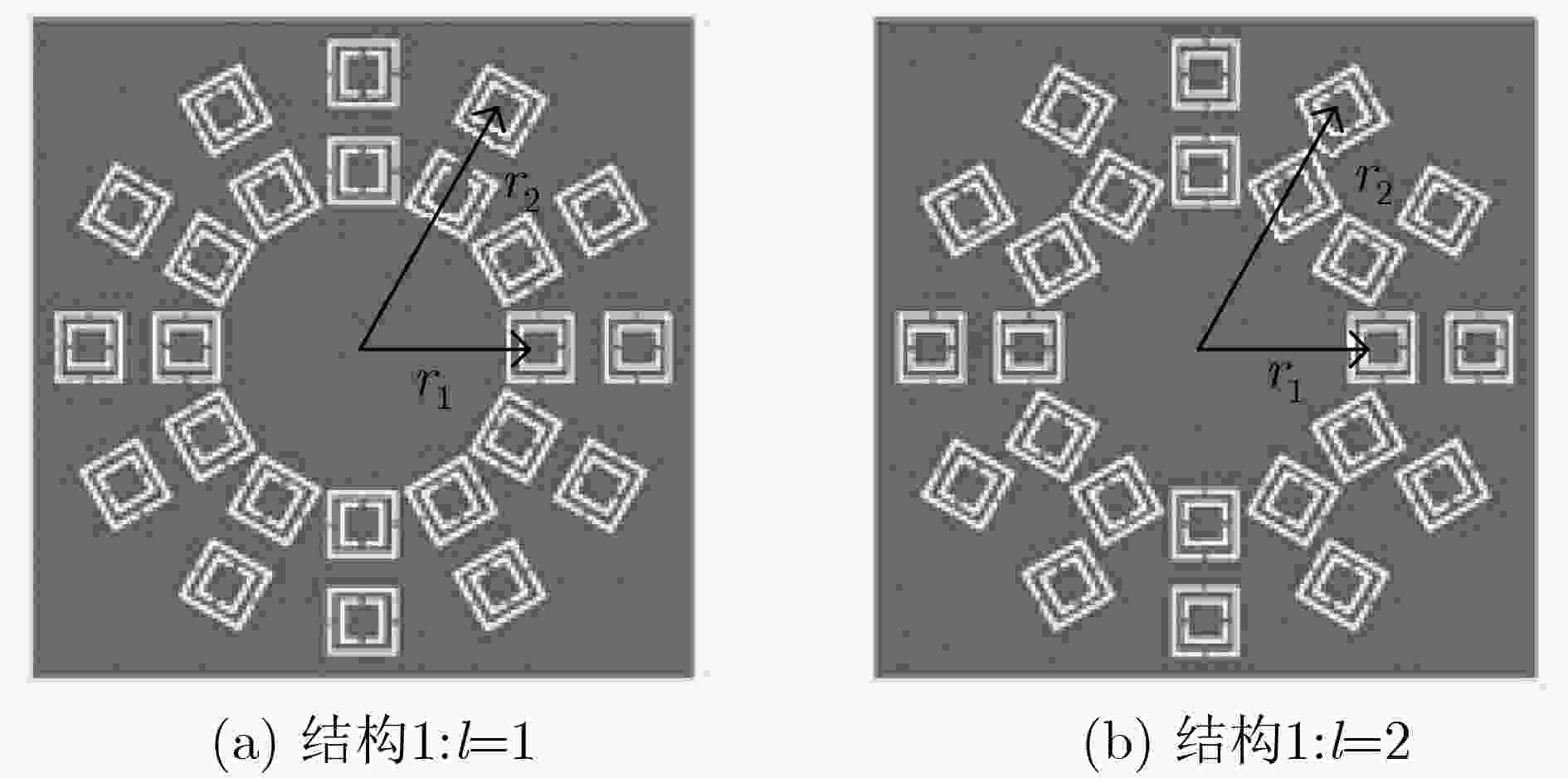
螺旋抛物面天线成本低、系统复杂度较低、转换效率和转换速度正常;但是仅能在单点频率上生成单模态和非纯模态,并且实现过程较复杂。 通过OAM编码技术实现同频宽带干扰和地面反射干扰的鲁棒性传输。 天线阵列 为各阵列单元馈送相同信号,通过改变阵元间馈电相位差产生不同的模态。 圆形相控阵列时间开关阵列巴特勒矩阵馈电阵列光实时延时天线阵列 可在所有频率范围内生成多个模态和相反模态,器件制作较容易,转换速度和效率一般;但是成本高、系统复杂度较高。 可对携带OAM的射频信号进行多路复用和解复用,增加系统容量和效率。 q-板 在普通介质材料上加工特定几何形状的凹槽形成一种非均匀双折射结构。 – 成本低、系统复杂度较低、转换速度一般;但是仅能在单点频率处生成单模态,实现过程也较复杂。 可用于100 GHz毫米波OAM波束的产生和检测[30]。 表 3 基于超表面的电磁涡旋产生方法比较
表 4 典型的OAM检测方法
检测方法 结构 基本原理 优缺点 结果 单点法 – 利用OAM远场近似,对检测点上电场和磁场的
所有3个分量进行模式分析,计算得出
在空间特定点上的拓扑电荷值。成本低、系统复杂度较低;需对整个波前进行采样;适用于单模态和较低模态的检测。 – 相位梯度法 – 检测两点间相位梯度,通过螺旋相位结构判定OAM模态。 成本低、系统复杂度较低;仅需分析波前上的两个采样点,适用于单模态检测。 – 多环谐振器OAM
天线经验模式分解 电磁波的基础可以由经验模式分解中的固有模式函数构成,由此定义每个局部拓扑电荷。 能够检测叠加态。 检测了-2和3的叠加态 数字虚拟旋转
天线接收天线高速采样示波器频谱分析仪 根据旋转多普勒频移和OAM模态之间的关系确定OAM模态。 系统较复杂;适用于检测单个模态。 检测了1, 2, 4共3个单模态 衍射模式转换器 OAM模式转换器,接收天线 SPP板产生不同模态涡旋波束;模式转换器将涡旋波束映射为平面波,通过透镜聚焦产生横向光斑,最后接收。 成本较低;需检测整个波前,但是适用于单模态和叠加态的检测。 检测了–3到3共7个单模态和两个叠加态 全息超表面 全息超表面 超表面将OAM波束转换为高斯波束,通过定位高斯波束在设定位置处的场强确定入射OAM模态。 系统复杂度较低;成本高、器件实现较复杂;适用于多个单模态的检测。 检测了–2到2共5个单模态 部分孔径取样接收法 – 将光学中用于OAM解复用的偏角接收孔径法和采样接收法结合。 仅需对部分波前进行采样,以检测多个模态;成本高; – 均匀圆形天线
阵列对接收到的电磁涡旋进行频谱分析。 可检测相反模态和但,模态;成本高,需对整个波前采样,系统复杂度高。 表 5 OAM与LTE传输速率和频谱利用率比较
通信类型 频谱利用率(bps/Hz) 传输速率(Mbps) 调制方式 OAM 95.5 2560 16-QAM[16] LTE 16.32 326.4 64-QAM -
POYNTING J H. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1909, 82(557): 560–567. DARWIN C G. Notes on the theory of radiation[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1932, 136(829): 36–52. ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185–8189. doi: 10.1103/PhysRevA.45.8185 TAO S H, YUAN X C, LIN J, et al. Fractional optical vortex beam induced rotation of particles[J]. Optics Express, 2005, 13(20): 7726–7731. doi: 10.1364/OPEX.13.007726 SIMPSON N B, DHOLAKIA K, ALLEN L, et al. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner[J]. Optics Letters, 1997, 22(1): 52–54. doi: 10.1364/OL.22.000052 DI TRAPANI P, CHINAGLIA W, MINARDI S, et al. Observation of quadratic optical vortex solitons[J]. Physical Review Letters, 2000, 84(17): 3843–3846. doi: 10.1103/PhysRevLett.84.3843 POPESCU G and DOGARIU A. Spectral anomalies at wave-front dislocations[J]. Physical Review Letters, 2002, 88(18): 183902. doi: 10.1103/PhysRevLett.88.183902 BERŽANSKIS A, MATIJOŠLUS A, PISKARSKAS A, et al. Conversion of topological charge of optical vortices in a parametric frequency converter[J]. Optics Communications, 1997, 140(4/6): 273–276. GIBSON G, COURTIAL J, PADGETT M J, et al. Free-space information transfer using light beams carrying orbital angular momentum[J]. Optics Express, 2004, 12(22): 5448–5456. doi: 10.1364/OPEX.12.005448 XIE Guodong, REN Yongxiong, YAN Yan, et al. Experimental demonstration of a 200-Gbit/s free-space optical link by multiplexing Laguerre–Gaussian beams with different radial indices[J]. Optics Letters, 2016, 41(15): 3447–3450. doi: 10.1364/OL.41.003447 NDAGANO B, NAPE I, COX M A, et al. Creation and detection of vector vortex modes for classical and quantum communication[J]. Journal of Lightwave Technology, 2018, 36(2): 292–301. doi: 10.1109/JLT.2017.2766760 YUAN Tiezhu, WANG Hongqiang, CHENG Yongqiang, et al. Electromagnetic vortex-based radar imaging using a single receiving antenna: Theory and experimental results[J]. Sensors, 2017, 17(3): 630. doi: 10.3390/s17030630 LIN Mingtuan, LIU Peiguo, GAO Yue, et al. Super-resolution orbital angular momentum based radar targets detection[J]. Electronics Letters, 2016, 52(13): 1168–1170. doi: 10.1049/el.2016.0237 SHI Chengzhi, DUBOIS M, WANG Yuan, et al. High-speed acoustic communication by multiplexing orbital angular momentum[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(28): 7250–7253. doi: 10.1073/pnas.1704450114 THIDÉ B, THEN H, SJÖHOLM J, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8): 087701. doi: 10.1103/PhysRevLett.99.087701 WANG Jian, YANG J Y, FAZAL I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics, 2012, 6(7): 488–496. doi: 10.1038/nphoton.2012.138 TAMBURINI F, MARI E, SPONSELLI A, et al. Encoding many channels on the same frequency through radio vorticity: First experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. doi: 10.1088/1367-2630/14/3/033001 PADGETT M J. Orbital angular momentum 25 years on [Invited][J]. Optics Express, 2017, 25(10): 11265–11274. doi: 10.1364/OE.25.011265 刘康, 黎湘, 王宏强, 等. 涡旋电磁波及其在雷达中应用研究进展[J]. 电子学报, 2018, 46(9): 2283–2290. doi: 10.3969/j.issn.0372-2112.2018.09.034LIU Kang, LI Xiang, WANG Hongqiang, et al. The advances of vortex electromagnetic wave in radar applications[J]. Acta Electronica Sinica, 2018, 46(9): 2283–2290. doi: 10.3969/j.issn.0372-2112.2018.09.034 CHENG Wenchi, ZHANG Wei, JING Haiyue, et al. Orbital angular momentum for wireless communications[J]. IEEE Wireless Communications, 2019, 26(1): 100–107. doi: 10.1109/MWC.2017.1700370 JING Haiyue, CHENG Wenchi, LI Zan, et al. Concentric UCAs based low-order OAM for high capacity in radio vortex wireless communications[J]. Journal of Communications and Information Networks, 2018, 3(4): 85–100. doi: 10.1007/s41650-018-0036-z CHENG Wenchi, ZHANG Hailin, LIANG Liping, et al. Orbital-angular-momentum embedded massive MIMO: Achieving multiplicative spectrum-efficiency for mmwave communications[J]. IEEE Access, 2018, 6: 2732–2745. doi: 10.1109/ACCESS.2017.2785125 LIANG Liping, CHENG Wenchi, ZHANG Wei, et al. Mode hopping for anti-jamming in radio vortex wireless communications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(8): 7018–7032. doi: 10.1109/TVT.2018.2825539 孙学宏, 李强, 庞丹旭, 等. 轨道角动量在无线通信中的研究新进展综述[J]. 电子学报, 2015, 43(11): 2305–2314. doi: 10.3969/j.issn.0372-2112.2015.11.025SUN Xuehong, LI Qiang, PANG Danxu, et al. New research progress of the orbital angular momentum technology in wireless communication: A survey[J]. Acta Electronica Sinica, 2015, 43(11): 2305–2314. doi: 10.3969/j.issn.0372-2112.2015.11.025 MOHAMMADI S M, DALDORFF L K S, BERGMAN J E S, et al. Orbital angular momentum in radio—a system study[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(2): 565–572. doi: 10.1109/TAP.2009.2037701 TAMBURINI F, THIDÉ B, MARI E, et al. Reply to comment on ‘encoding many channels on the same frequency through radio vorticity: First experimental test’[J]. New Journal of Physics, 2012, 14(11): 118002. doi: 10.1088/1367-2630/14/11/118002 BOUCHAL Z and CELECHOVSKY R. Mixed vortex states of light as information carriers[J]. New Journal of Physics, 2004, 6(1): 131. MAIR A, VAZIRI A, WEIHS G, et al. Entanglement of the orbital angular momentum states of photons[J]. Nature, 2001, 412(6844): 313–316. doi: 10.1038/35085529 CHEN Menglin, JIANG Lijun, and SHA Wei. Orbital angular momentum generation and detection by geometric-phase based metasurfaces[J]. Applied Sciences, 2018, 8(3): 362. doi: 10.3390/app8030362 MACCALLI S, PISANO G, COLAFRANCESCO S, et al. Q-plate for millimeter-wave orbital angular momentum manipulation[J]. Applied Optics, 2013, 52(4): 635–639. doi: 10.1364/AO.52.000635 KOU Na, YU Shixing, and LI Long. Generation of high-order Bessel vortex beam carrying orbital angular momentum using multilayer amplitude-phase-modulated surfaces in radiofrequency domain[J]. Applied Physics Express, 2017, 10(1): 016701. doi: 10.7567/APEX.10.016701 CHEN Menglin, JIANG Lijun, and SHA Wei. Artificial perfect electric conductor-perfect magnetic conductor anisotropic metasurface for generating orbital angular momentum of microwave with nearly perfect conversion efficiency[J]. Journal of Applied Physics, 2016, 119(6): 064506. doi: 10.1063/1.4941696 GUO Yinghui, PU Mingbo, ZHAO Zeyu, et al. Merging geometric phase and plasmon retardation phase in continuously shaped metasurfaces for arbitrary Orbital angular momentum generation[J]. ACS Photonics, 2016, 3(11): 2022–2029. doi: 10.1021/acsphotonics.6b00564 KARIMI E, SCHULZ S A, DE LEON I, et al. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface[J]. Light: Science & Applications, 2014, 3(5): e167. MA Xiaoliang, PU Mingbo, LI Xiong, et al. A planar chiral meta-surface for optical vortex generation and focusing[J]. Scientific Reports, 2015, 5: 10365. doi: 10.1038/srep10365 CHEN Menglin, JIANG Lijun, and SHA Wei. Ultrathin complementary metasurface for orbital angular momentum generation at microwave frequencies[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(1): 396–400. doi: 10.1109/TAP.2016.2626722 CHEN Menglin, JIANG Lijun, and SHA Wei. Generation of orbital angular momentum by a point defect in photonic crystals[J]. Physical Review Applied, 2018, 10(1): 014034. doi: 10.1103/PhysRevApplied.10.014034 XU Bijun, WU Chao, WEI Zeyong, et al. Generating an orbital-angular-momentum beam with a metasurface of gradient reflective phase[J]. Optical Materials Express, 2016, 6(12): 3940–3945. doi: 10.1364/OME.6.003940 SHI Hongyu, WANG Luyi, PENG Gantao, et al. Generation of multiple modes microwave vortex beams using active metasurface[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(1): 59–63. doi: 10.1109/LAWP.2018.2880732 CHEN Menglin, JIANG Lijun, and SHA Wei. Quasi-continuous metasurfaces for orbital angular momentum generation[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(3): 477–481. doi: 10.1109/LAWP.2019.2894772 ZHENG Shilie, DONG Ruofan, ZHANG Zhuofan, et al. Non-line-of-sight channel performance of plane spiral orbital angular momentum MIMO systems[J]. IEEE Access, 2017, 5: 25377–25384. doi: 10.1109/ACCESS.2017.2766078 YAN Yan, LI Long, XIE Guodong, et al. Experimental measurements of multipath-induced intra- and inter-channel crosstalk effects in a millimeter-wave communications link using orbital-angular-momentum multiplexing[C]. 2015 IEEE International Conference on Communications, London, UK, 2015: 1370–1375. YAO Yu, LIANG Xianlin, ZHU Maohua, et al. Analysis and experiments on reflection and refraction of orbital angular momentum waves[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(4): 2085–2094. doi: 10.1109/TAP.2019.2896760 ZHANG Runzhou, LI Long, ZHAO Zhe, et al. Coherent optical wireless communication link employing orbital angular momentum multiplexing in a ballistic and diffusive scattering medium[J]. Optics Letters, 2019, 44(3): 691–694. doi: 10.1364/OL.44.000691 NIEMIEC R, BROUSSEAU C, EMILE O, et al. Study of OAM waves reflection on different types of surfaces or objects at 2.45 GHz[C]. The 1st URSI Atlantic Radio Science Conference, Las Palmas, Spain, 2015: 1–2. CHEN Menglin, JIANG Lijun, and SHA Wei. Detection of orbital angular momentum with metasurface at microwave band[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(1): 110–113. doi: 10.1109/LAWP.2017.2777439 MOHAMMADI S M, DALDORFF L K S, FOROZESH K, et al. Orbital angular momentum in radio: Measurement methods[J]. Radio Science, 2010, 45(4): RS4007. HUI Xiaonan, ZHENG Shilie, ZHANG Weite, et al. Local topological charge analysis of electromagnetic vortex beam based on empirical mode decomposition[J]. Optics Express, 2016, 24(5): 5423–5430. doi: 10.1364/OE.24.005423 ZHANG Chao and MA Lu. Detecting the orbital angular momentum of electro-magnetic waves using virtual rotational antenna[J]. Scientific Reports, 2017, 7(1): 4585. doi: 10.1038/s41598-017-04313-4 LIU Changming, WEI Xuli, NIU Liting, et al. Discrimination of orbital angular momentum modes of the terahertz vortex beam using a diffractive mode transformer[J]. Optics Express, 2016, 24(12): 12534–12541. doi: 10.1364/OE.24.012534 ZHENG Shilie, JIN Xiaofeng, ZHANG Xianmin, et al. Simulation of orbital angular momentum radio communication systems based on partial aperture sampling receiving scheme[J]. IET Microwaves, Antennas & Propagation, 2016, 10(10): 1043–1047. 武华阳. 无线轨道角动量通信与雷达目标成像技术研究[D]. [硕士论文], 浙江大学, 2017.WU Huayang. Research on wireless communication and radar target imaging technique based on OAM[D]. [Master dissertation], Zhejiang University, 2017. LEE D, SASAKI H, FUKUMOTO H, et al. Orbital angular momentum (OAM) multiplexing: An enabler of a new era of wireless communications[J]. IEICE Transactions on Communications, 2017, 100(7): 1044–1063. 黄铭, 毛福春, 曾佳, 等. 轨道角动量复用技术[J]. 中国无线电, 2013(5): 34–36. doi: 10.3969/j.issn.1672-7797.2013.05.018HUANG Ming, MAO Fuchun, ZENG Jia, et al. Orbital angular momentum multiplexing technology[J]. China Radio, 2013(5): 34–36. doi: 10.3969/j.issn.1672-7797.2013.05.018 ZHANG Weite, ZHENG Shilie, HUI Xiaonan, et al. Mode division multiplexing communication using microwave orbital angular momentum: An experimental study[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 1308–1318. doi: 10.1109/TWC.2016.2645199 LI Yang, LI Xiong, CHEN Lianwei, et al. Orbital angular momentum multiplexing and demultiplexing by a single metasurface[J]. Advanced Optical Materials, 2017, 5(2): 1600502. doi: 10.1002/adom.201600502 ZHANG Di, CAO Xiangyu, GAO Jun, et al. A shared aperture 1 bit metasurface for orbital angular momentum multiplexing[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(4): 566–570. doi: 10.1109/LAWP.2019.2893492 OPARE K A, KUANG Yujun, and KPONYO J J. Mode combination in an ideal wireless OAM-MIMO multiplexing system[J]. IEEE Wireless Communications Letters, 2015, 4(4): 449–452. doi: 10.1109/LWC.2015.2434375 LEE D, SASAKI H, FUKUMOTO H, et al. An experimental demonstration of 28 GHz band wireless OAM-MIMO (orbital angular momentum multi-input and multi-output) multiplexing[C]. The 87th IEEE Vehicular Technology Conference, Porto, Portugal, 2018: 1–5. YAN Yan, LI Long, XIE Guodong, et al. OFDM over mm-wave OAM channels in a multipath environment with intersymbol interference[C]. 2016 IEEE Global Communications Conference, Washington, USA, 2016: 1–6. CHEN Rui, YANG Wenhai, XU Hui, et al. A 2-D FFT-based transceiver architecture for OAM-OFDM systems with UCA antennas[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5481–5485. doi: 10.1109/TVT.2018.2817230 HU Tao, WANG Yang, LIAO Xi, et al. OFDM-OAM modulation for future wireless communications[J]. IEEE Access, 2019, 7: 59114–59125. doi: 10.1109/ACCESS.2019.2915035 GOU Pengqi, KONG Miao, YANG Guomin, et al. Integration of OAM and WDM in optical wireless system by radial uniform circular array[J]. Optics Communications, 2018, 424: 159–162. doi: 10.1016/j.optcom.2018.04.059 YAN Yan, XIE Guodong, LAVERY M P J, et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing[J]. Nature Communications, 2014, 5: 4876. doi: 10.1038/ncomms5876 观察者. 中国完成世界首次微波频段轨道角动量电磁波27.5公里长距离传输实验[EB/OL]. https://www.guancha.cn/Science/2017_02_22_395395.shtml, 2017.Guancha Syndicate. China has completed the world's first long-distance transmission experiment of 27.5 km of microwave frequency orbital angular momentum electromagnetic wave[EB/OL]. https://www.guancha.cn/Science/2017_02_22_395395.shtml, 2017. TAMAGNONE M, CRAEYE C, and PERRUISSEAU-CARRIER J. Comment on ‘encoding many channels on the same frequency through radio vorticity: First experimental test’[J]. New Journal of Physics, 2012, 14(11): 118001. doi: 10.1088/1367-2630/14/11/118001 -





 下载:
下载:
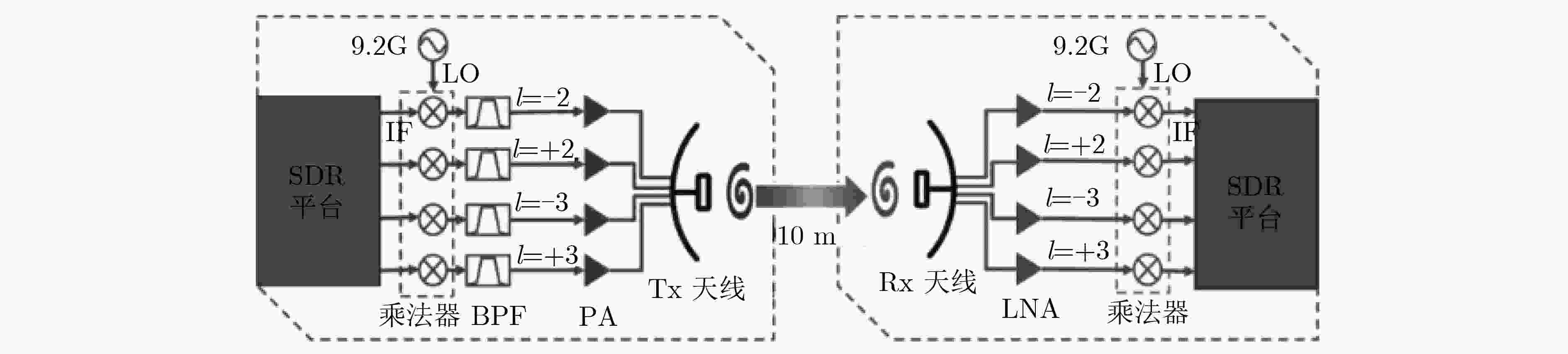
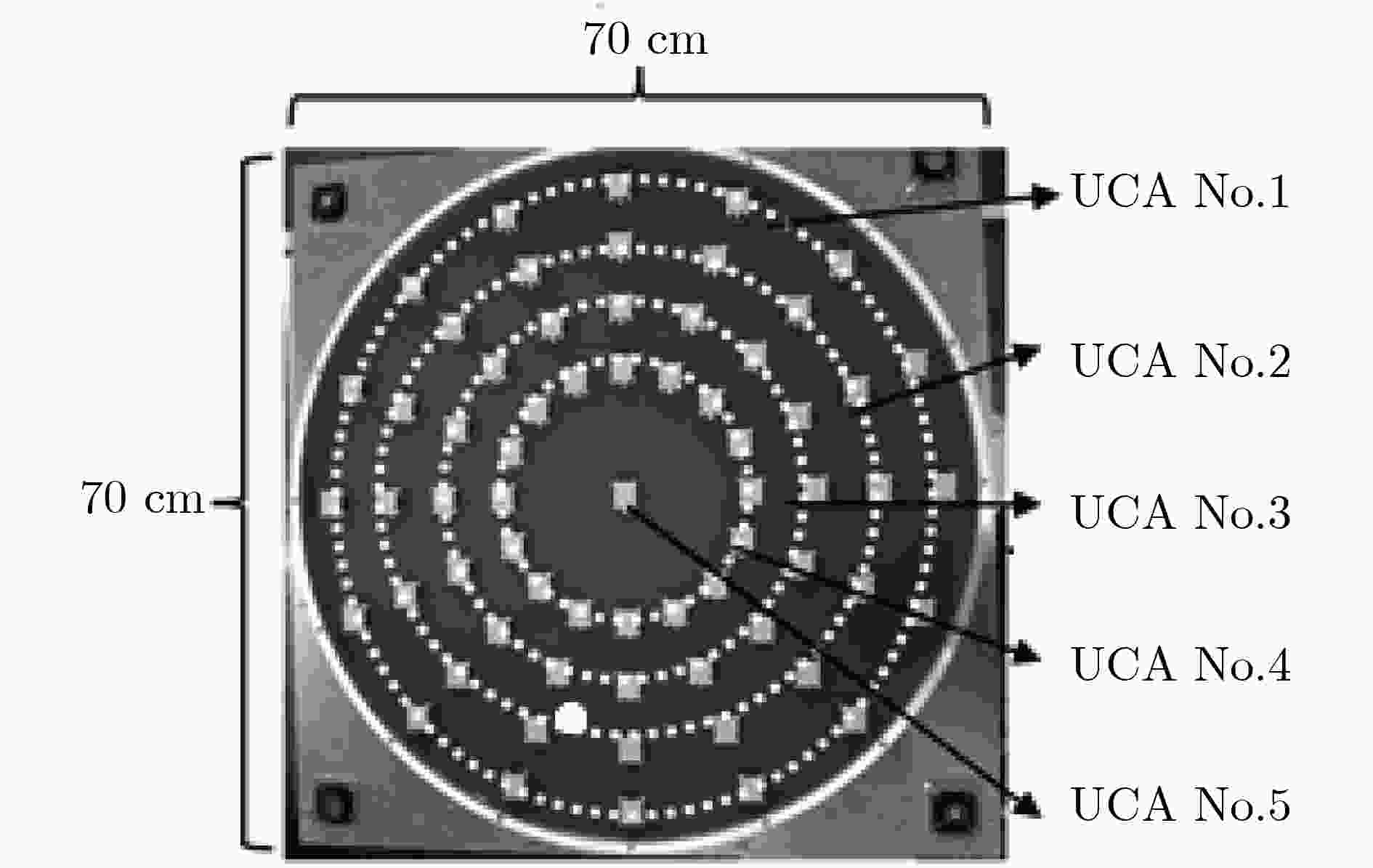
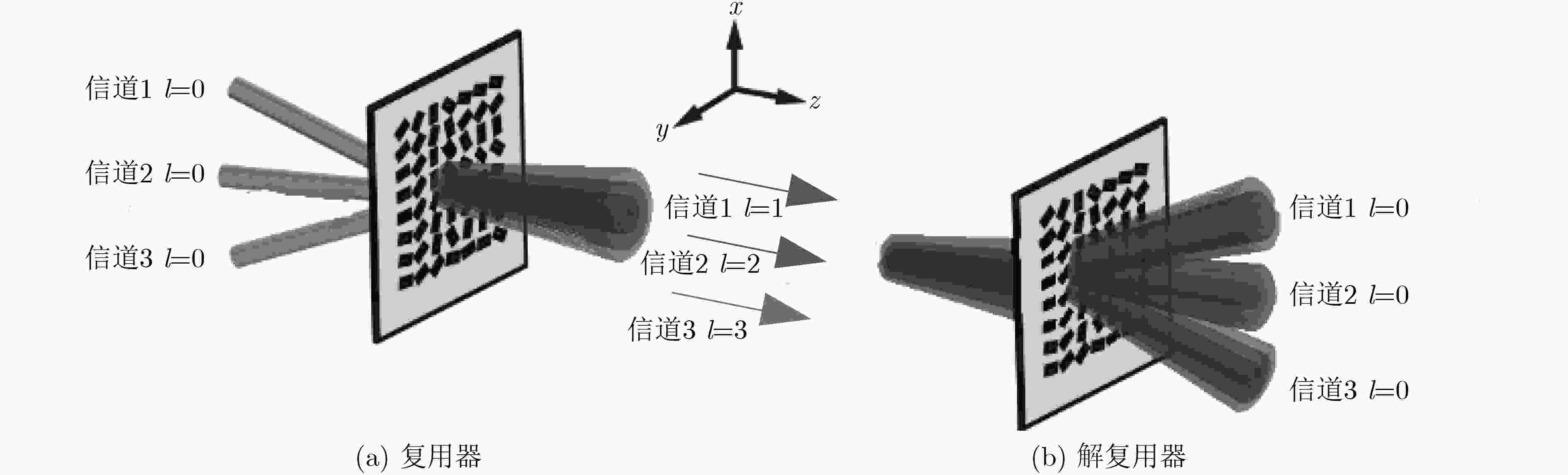


 下载:
下载:
