Earthquake Emergency Resource Multiobjective Schedule Algorithm Based on Particle Swarm Optimization
-
摘要:
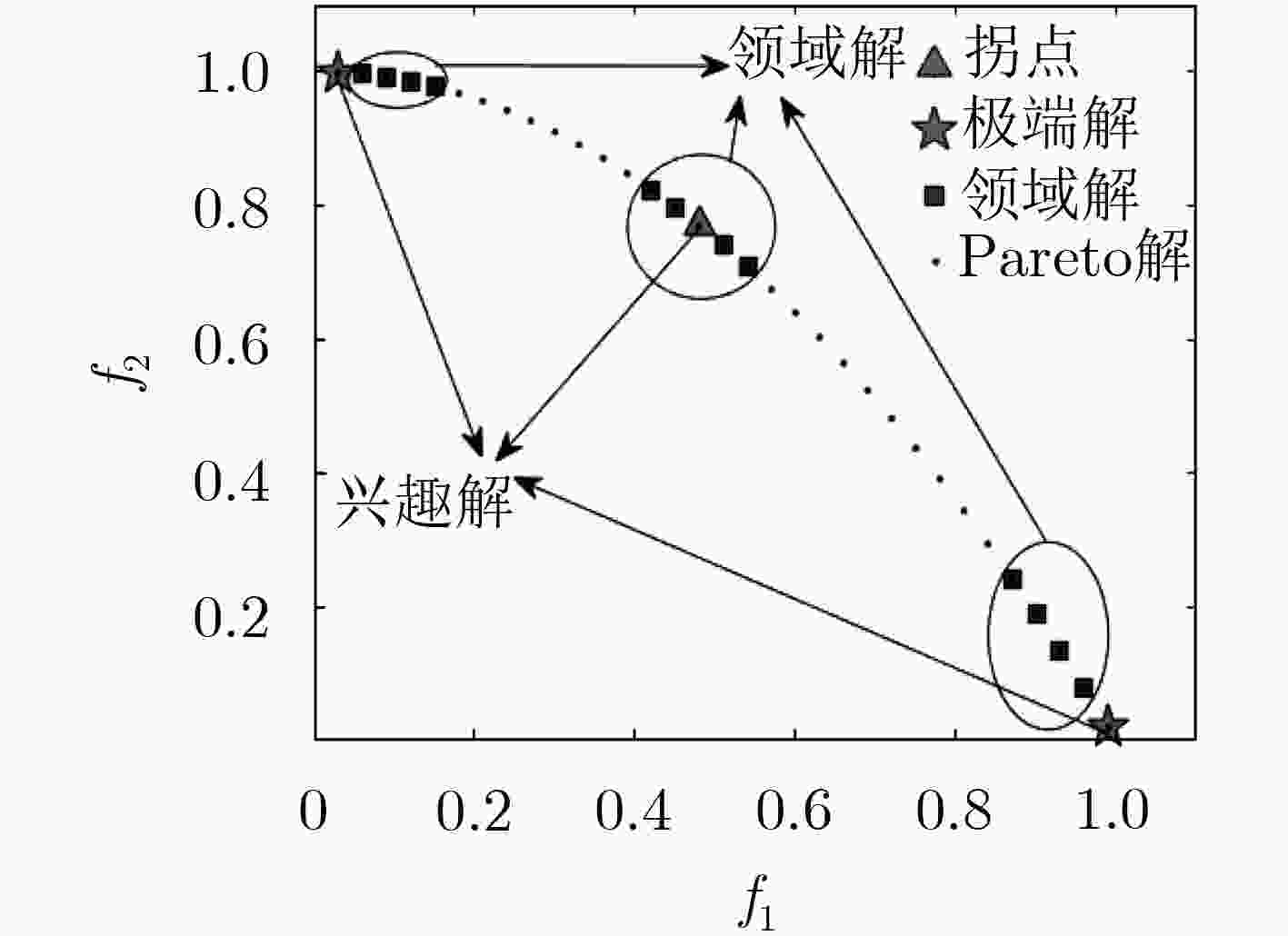
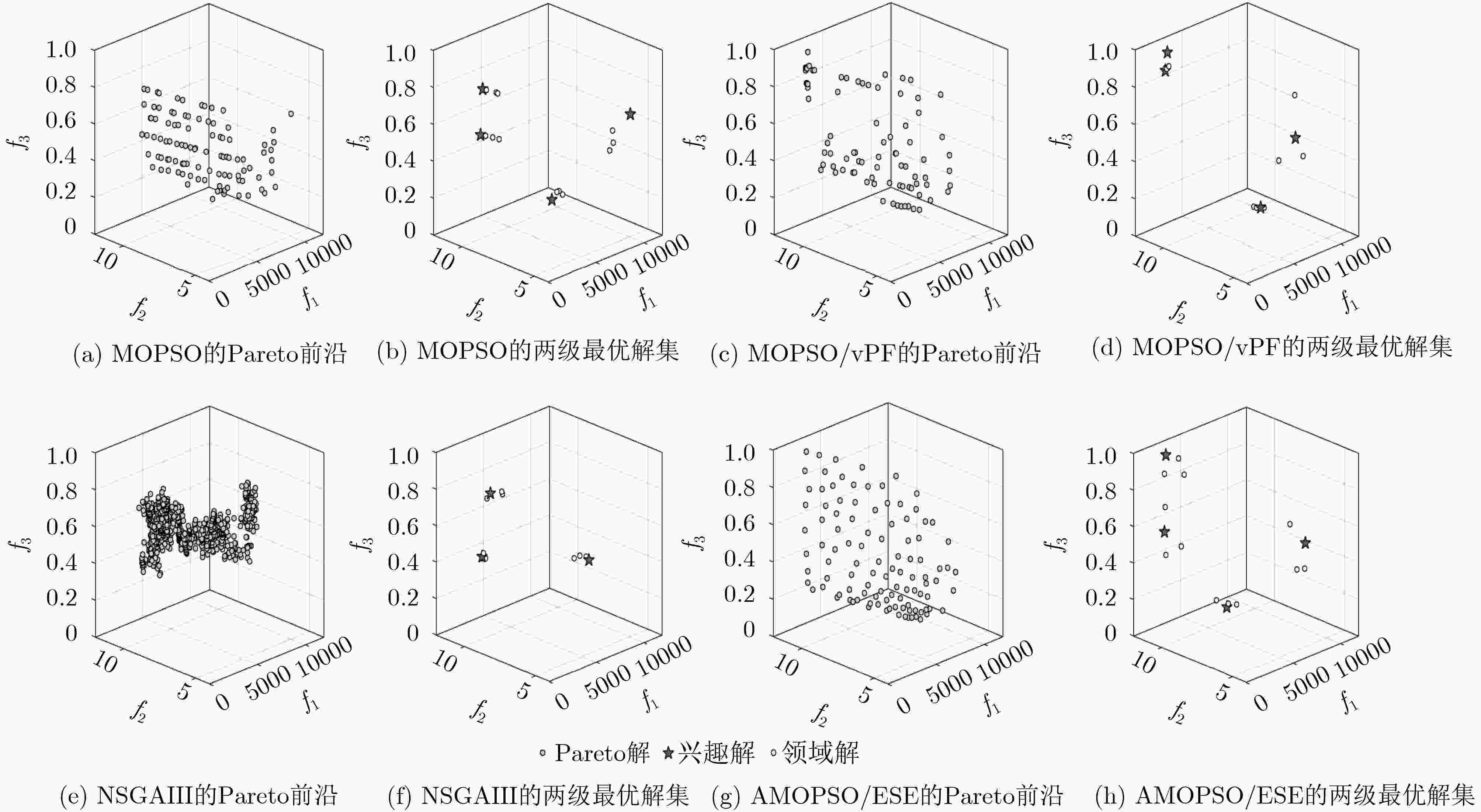
合理高效地优化调度救灾物资对提升地震应急救援效果具有重要意义。地震应急需要同时兼顾时效性、公平性和经济性等相互冲突的多个调度目标。该文对地震应急物资调度问题建立了带约束的3目标优化模型，并设计了基于进化状态评估的自适应多目标粒子群优化算法(AMOPSO/ESE)来求解Pareto最优解集。然后根据“先粗后精”的决策行为模式提出了由兴趣最优解集和邻域最优解集构成的Pareto前沿来辅助决策过程。仿真表明该算法能有效地获得优化调度方案，与其他算法相比，所得Pareto解集在收敛性和多样性上具有性能优势。
Abstract:It is of great significance to optimize emergency resource schedule for earthquake emergency rescue. The conflicting multiple schedule goals, such as time, fairness, and cost, should be taken into consideration together in an earthquake emergency resource schedule. A three-objective optimization model with constraints is constructed according to earthquake emergency resource schedule problems. An Adaptive MultiObjective Particle Swarm Optimization (PSO) based on Evolutionary State Evaluation (AMOPSO/ESE) is proposed to optimize this model for obtaining the Pareto optimal set. At the same time, based on the decision behavior pattern of "macro first and micro later", the two-level optimal solution sets consisting of an interest optimal solution set and their neighborhood optimal solution sets are proposed to represent the Pareto front roughly, which can simplify the decision-making process. The simulation results show that the multiobjective resource schedules can be effectively obtained by the AMOPSO/ESE algorithm, and the performance of the proposed algorithm is better than that of the chosen competed algorithms in terms of convergence and diversity.
-
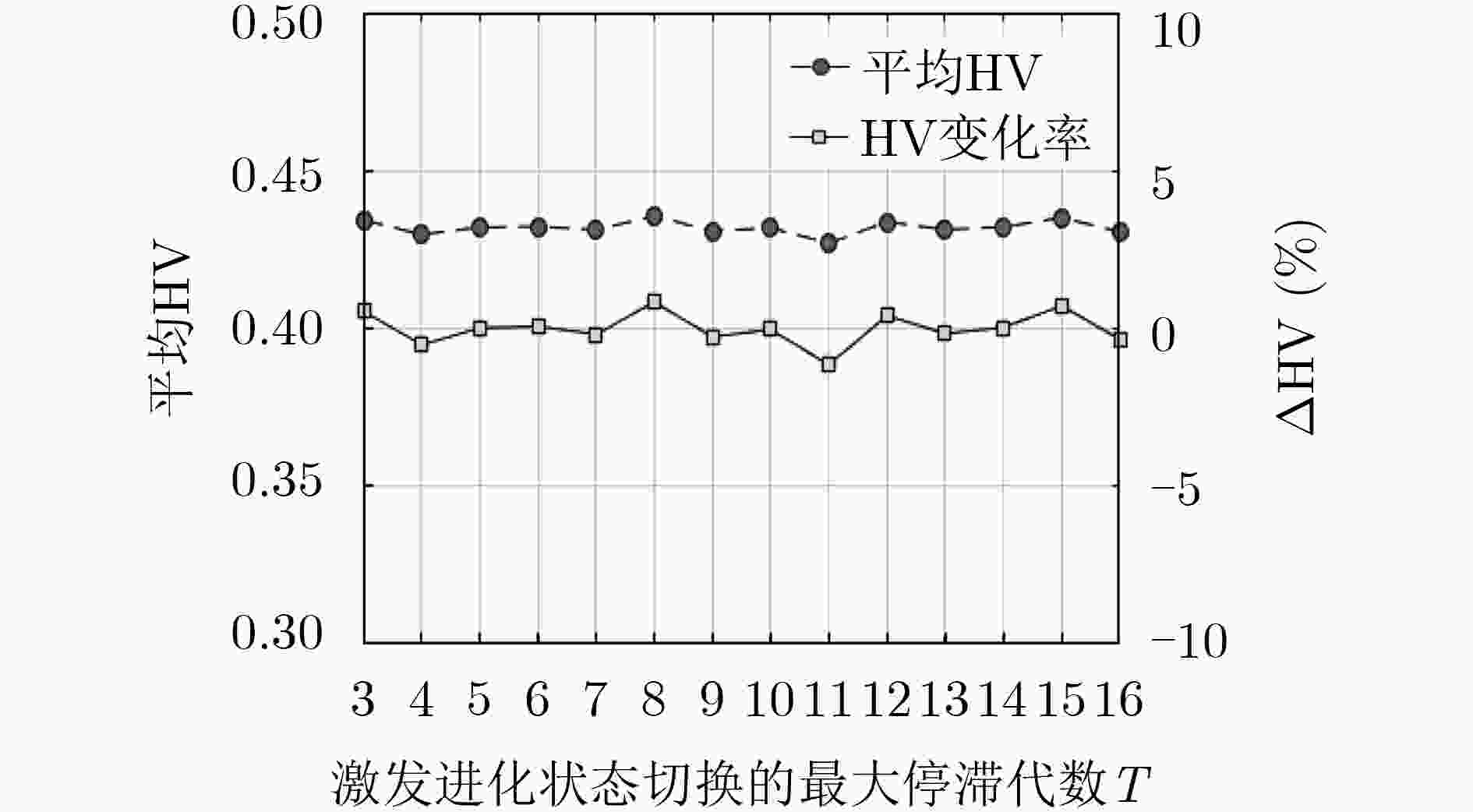
表 1 进化状态评估算
算法1 进化状态评估算法 输入：外部档案集A，到原点的历史最小距离Hmin，进化状态
ES，计数器Counter，状态切换阈值T。输出：更新后的进化状态${\rm ES}' $，计数器新值${\rm Counter}' $，更新后的
历史最小距离$H{\rm min}' $。(1) 计算A中每个解i到原点之间的距离，AD[i]； (2) 将距离矩阵AD中的最小值赋予Amin； (3) 若 ES为进化状态EXPLOITATION (4) 若Hmin ≤ Amin (5) 计数器Counter =Counter + 1； (6) 若计数器 Counter 大于状态切换阈T (7) 则${\rm ES}' $切换为进化状态EXPLORATION； (8) 否则， (9) 将Amin赋值给$H{\rm min}' $； (10) 计数器Counter 重置为0； (11) 否则 (12) 若Hmin大于Amin (13) 计数器Counter置为 0； (14) 新进化状态${\rm ES}' $切换为EXPLOITATION； (15) 将Amin赋值给$H{\rm min}' $’； (16) 输出${\rm ES}' $, ${\rm Counter}' $, $H{\rm min}' $. 
下载: 导出CSV
表 2 地震应急物资多目标粒子群优化调度算法
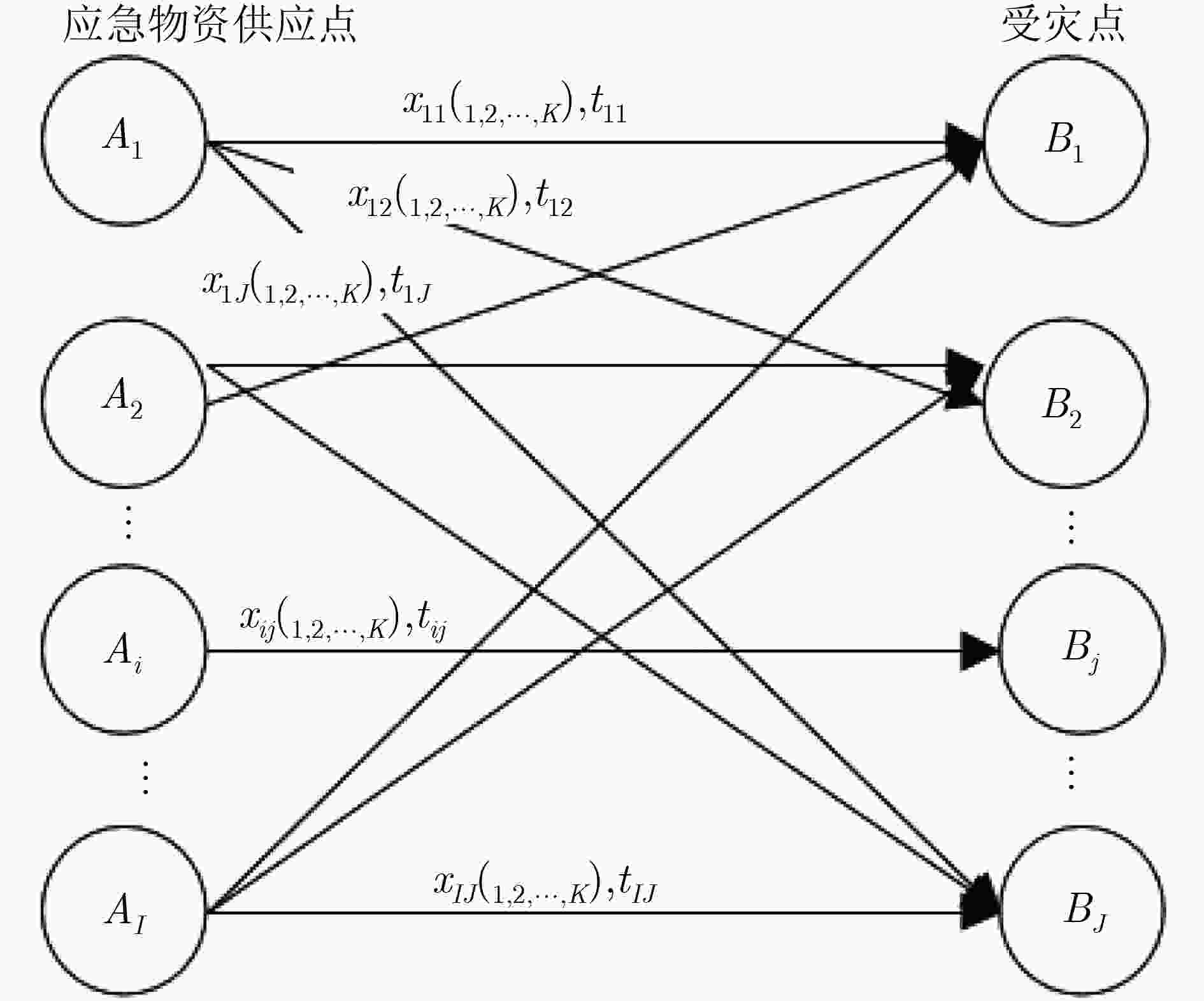
算法2 地震应急物资多目标粒子群优化调度算法 输入：(1) 物资供需参数：供应点和受灾点位置向量LS和Ld，
物资储备矩阵As，物资需求矩阵Ad，受灾点的优先系
数向量μd；(2) 算法控制参数：种群粒子数NP；外部档案AE容量
NA；最大迭代次数G；邻域最优解个数NN.输出：两级地震应急物资最优调度方案：兴趣最优解集A I和
邻域最优解集AN.(1) 根据位置向量Ls和Ld，以及灾后交通障碍信息计算供
应点和受灾点之间最短运输时间矩阵At；(2) 根据As和约束条件按3.1小节初始化种群P； (3) 将AE, AI和AN设置为空集Φ； (4) 根据式(1)，式(2)和式(3)中的多目标函数和At, As, Ad
及μd计算种群中每个粒子的适应值；(5) 令迭代次数t = 0； (6) While t ≤ G (a) 根据3.2小节的外部档案更新策略更新AE； (b) 根据3.3小节的最优解选择策略更新每个粒子的个
体最优解和种群的全局最优解；(c) 根据算法1评估进化状态，自适应调节惯性系数ω，
自我认知系数c1和社会认知系数c2，并根据粒子运动方
程更新粒子速度和位置；(d) 根据式(1)，式(2)和式(3)中的多目标函数和At, As,
Ad和μd计算P 中每个粒子的适应值；(e) t = t + 1； (7) End； (8) 根据邻域最优解个数NN和外部档案AE构造两级最优
解集AI和AN；(9) 输出AI和AN.
下载: 导出CSV
表 7 最好、平均和最差的HV值
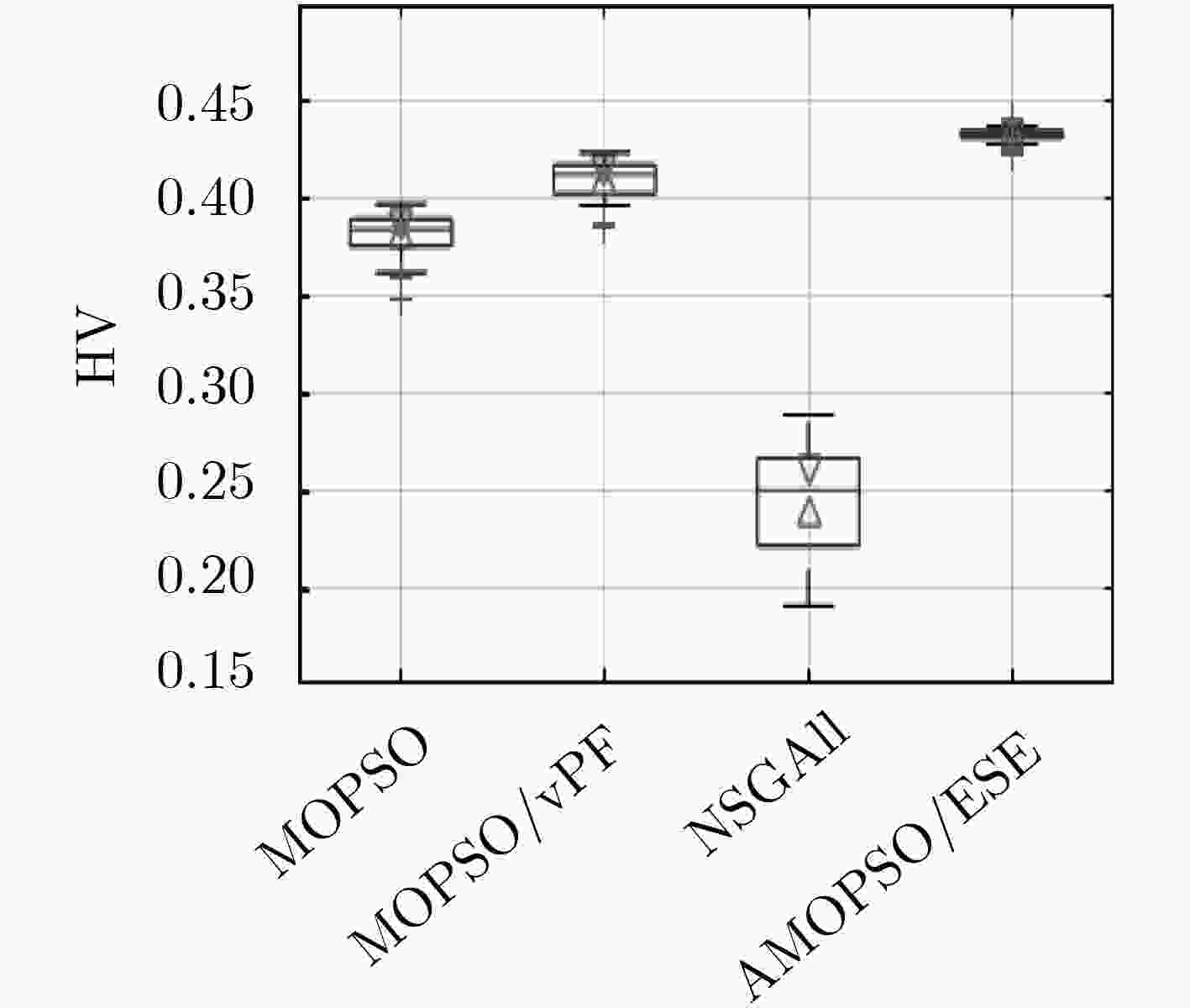
MOPSO MOPSO/vPF NSGAIII AMOPSO/ESE 最好 0.397272 0.423944 0.2886 0.440747 平均 0.380208 0.410418 0.2459 0.433046 最差 0.348903 0.386097 0.1902 0.422297
下载: 导出CSV
-
唐伟勤, 邹丽, 郭其云. 多应急点多需求点物资调度的灰色多目标规划[J]. 中国安全生产科学技术, 2016, 12(11): 148–152. doi: 10.11731/j.issn.1673-193x.2016.11.025TANG Weiqin, ZOU Li, and GUO Qiyun. Grey multi-objective programming for materials dispatching from multiple supply points to multiple demand points[J]. Journal of Safety Science and Technology, 2016, 12(11): 148–152. doi: 10.11731/j.issn.1673-193x.2016.11.025 范杰. 震后初期救灾物资两阶段调度优化研究[D]. [硕士论文], 北京交通大学, 2017.FAN Jie. Research on two-stage dispatching optimization of relief supplies early after the earthquake[D]. [Master dissertation], Beijing Jiaotong University, 2017. KENNEDY J and EBERHART R. Particle swarm optimization[C]. ICNN'95-International Conference on Neural Networks, Perth, Australia, 1995: 1942–1948. doi: 10.1109/ICNN.1995.488968. BONYADI M R and MICHALEWICZ Z. Particle swarm optimization for single objective continuous space problems: A review[J]. Evolutionary Computation, 2017, 25(1): 1–54. doi: 10.1162/EVCO_r_00180 COELLO C A C, PULIDO G T, and LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256–279. doi: 10.1109/TEVC.2004.826067 AL MOUBAYED N, PETROVSKI A, and MCCALL J. D 2MOPSO: MOPSO based on decomposition and dominance with archiving using crowding distance in objective and solution spaces[J]. Evolutionary Computation, 2014, 22(1): 47–77. doi: 10.1162/EVCO_a_00104 WU Bolin, HU Wang, HE Zhenan, et al. A many-objective particle swarm optimization based on virtual Pareto front[C]. IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 2018: 1–8. doi: 10.1109/CEC.2018.8477802. LI Li, WANG Wanliang, and XU Xinli. Multi-objective particle swarm optimization based on global margin ranking[J]. Information Sciences, 2017, 375: 30–47. doi: 10.1016/j.ins.2016.08.043 HU Wang and YEN G G. Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(1): 1–18. doi: 10.1109/tevc.2013.2296151 毕晓君, 张磊, 肖婧. 基于双种群的约束多目标优化算法[J]. 计算机研究与发展, 2015, 52(12): 2813–2823. doi: 10.7544/issn1000-1239.2015.20148025BI Xiaojun, ZHANG Lei, and XIAO Jing. Constrained multi-objective optimization algorithm based on dual populations[J]. Journal of Computer Research and Development, 2015, 52(12): 2813–2823. doi: 10.7544/issn1000-1239.2015.20148025 DEB K and JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577–601. doi: 10.1109/TEVC.2013.2281535 -
计量
- 文章访问数: 3340
- HTML全文浏览量: 1020
- PDF下载量: 121
- 被引次数: 0
下载:
