An Optimal Number of Indices Aided gOMP Algorithm for Multi-user Detection in NOMA System
-
摘要:
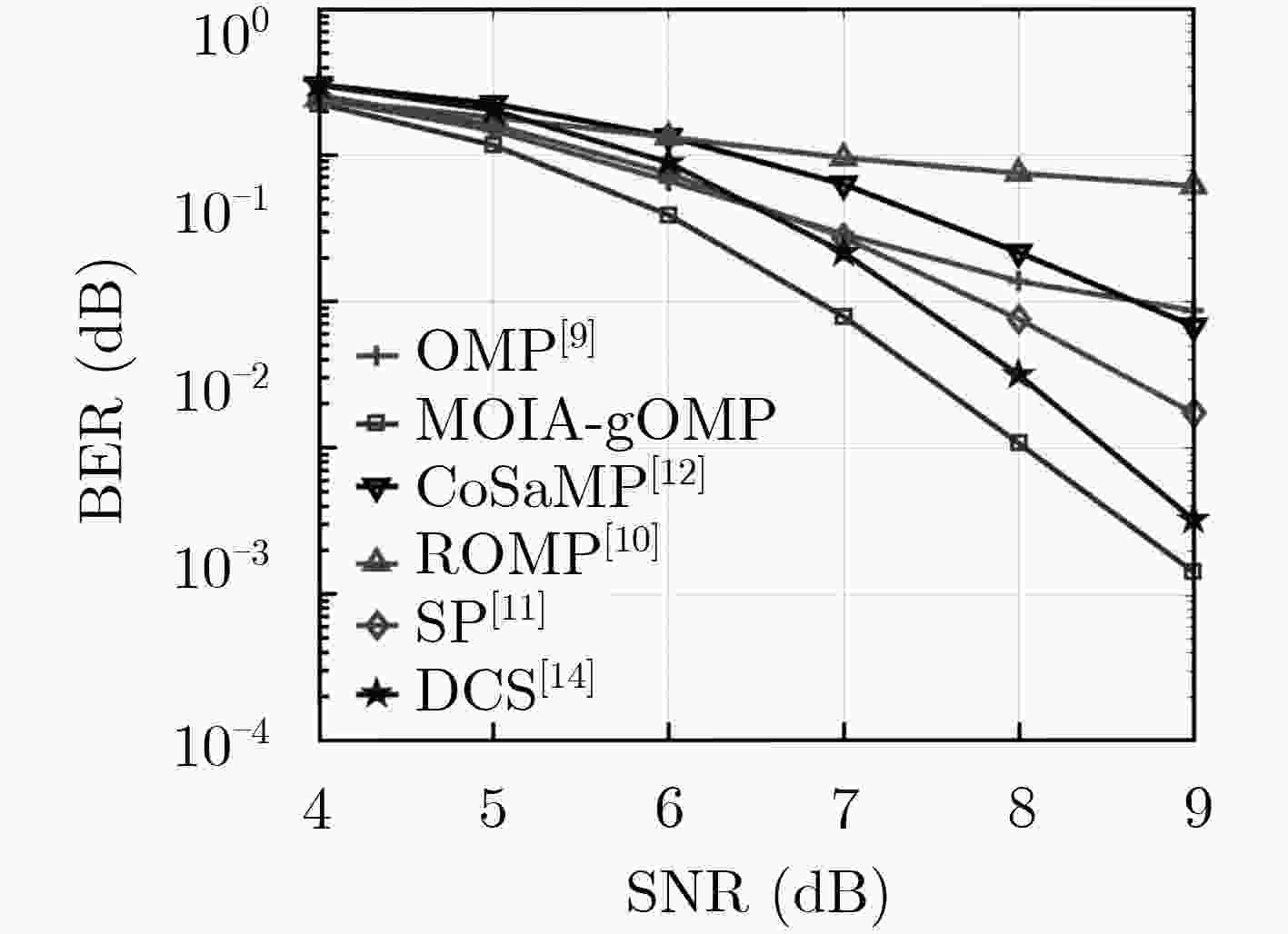
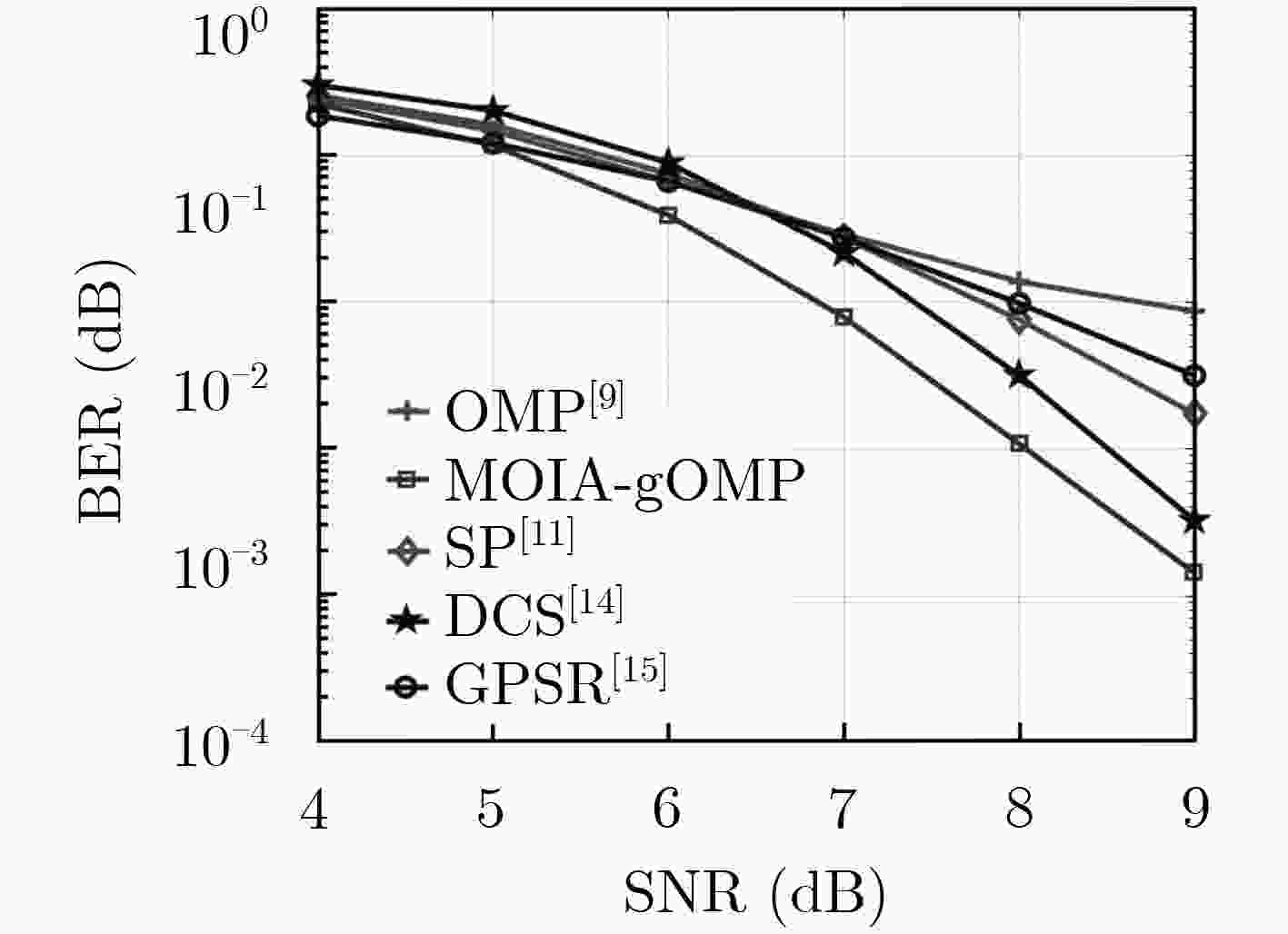
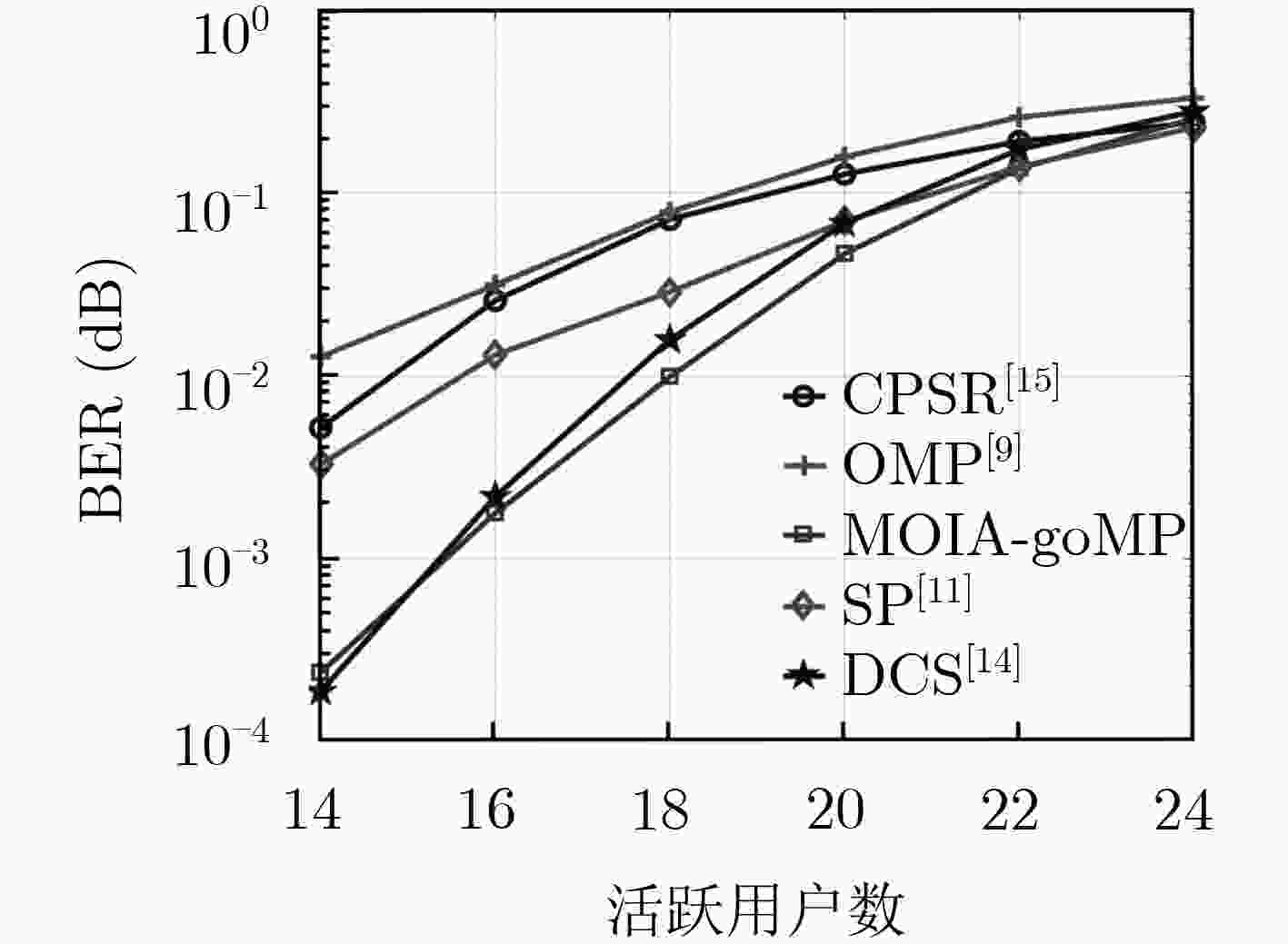
作为5G的关键技术之一,非正交多址(NOMA)通过非正交方式访问无线通信资源,以实现提高频谱利用率、增加用户连接数的目的。该文提出将压缩感知(CS)及广义正交匹配追踪(gOMP)算法引入上行免调度NOMA系统,从而增强NOMA系统活跃用户检测及数据接收的性能。通过每次迭代识别多个索引,gOMP算法实际上是传统的正交匹配追踪(OMP)算法的扩展。为了获得最优性能,研究分析了在gOMP算法信号重构的每次迭代中所应选择的最优索引数目。仿真结果表明:与其它的贪婪追踪算法及梯度投影稀疏重构(GPSR)算法相比,最优索引gOMP算法具有更优异的信号重构性能;并且,对于不同的活跃用户数或过载率等参数配置的NOMA系统,均表现出最优的多用户检测性能。
Abstract:As one of the key 5G technologies, Non-Orthogonal Multiple Access (NOMA) can improve spectrum efficiency and increase the number of user connections by utilizing the resources in a non-orthogonal manner. In the uplink grant-free NOMA system, the Compressive Sensing (CS) and generalized Orthogonal Matching Pursuit (gOMP) algorithm are introduced in active user and data detection, to enhance the system performance. The gOMP algorithm is literally generalized version of the Orthogonal Matching Pursuit (OMP) algorithm, in the sense that multiple indices are identified per iteration. Meanwhile, the optimal number of indices selected per iteration in the gOMP algorithm is addressed to obtain the optimal performance. Simulations verify that the gOMP algorithm with optimal number of indices has better recovery performance, compared with the greedy pursuit algorithms and the Gradient Projection Sparse Reconstruction (GPSR) algorithm. In addition, given different system configurations in terms of the number of active users and subcarriers, the proposed gOMP with optimal number of indices also exhibits better performance than that of the other algorithms mentioned in this paper.
-
表 1 最优索引gOMP检测算法
算法1 最优索引gOMP检测算法 输入 ${{y}}$, ${{H}}$, $S$, ${C_{{\rm{opt}}}}$. 初始化:${{{r}}^0} = {{y}}$,${{{\varGamma}} ^0} = \varnothing $,$t = 0$. (1) While ${\left\| {{{{r}}^t}} \right\|_2} > e$ 且$t \le S$ do (2) $t = t + 1$;
(3) $\eta {\rm{(}}i{\rm{)}} = \mathop {{\rm{argmax}}}\limits_{j:j \in \varOmega \backslash {\rm{\{ }}\eta {\rm{(}}i - 1{\rm{)}}, \cdots ,\eta {\rm{(2)}},\eta {\rm{(}}1{\rm{)\} }}} \left| { < {{{r}}^{t - 1}},{{{\varphi}} _j} > } \right|$;(4) ${{{\varGamma}} ^t} = {{{\varGamma}} ^{t - 1}} \cup {\rm{\{ }}\eta {\rm{(1),}}\eta {\rm{(2),}} ··· ,\eta {\rm{(}}{C_{{\rm{opt}}}}{\rm{)\} }}$; (5) ${\hat {{x} }_{ { {{\varGamma} } ^t} } } = \mathop { {\rm{argmin} } }\limits_{ u} {\left\| { {{y} } - { {{H} }_{ { {{\varGamma} } ^t} } }{{u} } } \right\|_2} = {{H} }_{ { {{\varGamma} } ^t} }^{\rm{† } }{{y} }$; (6) ${{{r}}^t} = {{y}} - {{{H}}_{{{{\varGamma}} ^t}}}{\hat {{x}}_{{{{\varGamma}} ^t}}}$ end while
输出 ${\hat {{x} }_{ { {{\varGamma} } ^t} } } = \mathop { {\rm{argmin} } }\limits_{ u} {\left\| { {{y} } - { {{H} }_{ { {{\varGamma} } ^t} } }{{u} } } \right\|_2}$ -
OSSEIRAN A, BOCCARDI F, BRAUN V, et al. Scenarios for 5G mobile and wireless communications: The vision of the METIS project[J]. IEEE Communications Magazine, 2014, 52(5): 26–35. doi: 10.1109/MCOM.2014.6815890 DAI Linglong, WANG Bichai, DING Zhiguo, et al. A survey of non-orthogonal multiple access for 5G[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2294–2323. doi: 10.1109/COMST.2018.2835558 DAI Linglong, WANG Bichai, YUAN Yifei, et al. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 74–81. doi: 10.1109/MCOM.2015.7263349 ISLAM S M R, AVAZOV N, DOBRE O A, et al. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 721–742. doi: 10.1109/COMST.2016.2621116 HONG J P, CHOI W, and RAO B D. Sparsity controlled random multiple access with compressed sensing[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 998–1010. doi: 10.1109/TWC.2014.2363165 CHOI J W, SHIM B, DING Yacong, et al. Compressed sensing for wireless communications: Useful tips and tricks[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1527–1550. doi: 10.1109/COMST.2017.2664421 李燕龙, 陈晓, 詹德满, 等. 非正交多址接入中稀疏多用户检测方法[J]. 西安电子科技大学学报: 自然科学版, 2017, 44(3): 151–156. doi: 10.3969/j.issn.1001-2400.2017.03.026LI Yanlong, CHEN Xiao, ZHEN Deman, et al. Method of sparse multi-user detection in non-orthogonal multiple access[J]. Journal of Xidian University, 2017, 44(3): 151–156. doi: 10.3969/j.issn.1001-2400.2017.03.026 SHIM B and SONG B. Multiuser detection via compressive sensing[J]. IEEE Communications Letters, 2012, 16(7): 972–974. doi: 10.1109/LCOMM.2012.050112.111980 TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108 NEEDELL D and VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 310–316. doi: 10.1109/JSTSP.2010.2042412 DAI Wei and MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230–2249. doi: 10.1109/TIT.2009.2016006 NEEDELL D and TROPP J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301–321. doi: 10.1016/j.acha.2008.07.002 WANG Jian, KWON S, and SHIM B. Generalized orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6202–6216. doi: 10.1109/TSP.2012.2218810 WANG Bichai, DAI Linglong, ZHANG Yuan, et al. Dynamic compressive sensing-based multi-user detection for uplink grant-free NOMA[J]. IEEE Communications Letters, 2016, 20(11): 2320–2323. doi: 10.1109/LCOMM.2016.2602264 FIGUEIREDO M A T, NOWAK R D, and WRIGHT S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586–597. doi: 10.1109/JSTSP.2007.910281 WANG Bichai, DAI Linglong, MIR T, et al. Joint user activity and data detection based on structured compressive sensing for NOMA[J]. IEEE Communications Letters, 2016, 20(7): 1473–1476. doi: 10.1109/LCOMM.2016.2560180 WEI Chao, LIU Huaping, ZHANG Zaichen, et al. Approximate message passing-based joint user activity and data detection for NOMA[J]. IEEE Communications Letters, 2017, 21(3): 640–643. doi: 10.1109/LCOMM.2016.2624297 CIRIK A C, BALASUBRAMANYA N M, and LAMPE L. Multi-user detection using ADMM-based compressive sensing for uplink grant-free NOMA[J]. IEEE Wireless Communications Letters, 2018, 7(1): 46–49. doi: 10.1109/LWC.2017.2752165 ZHU Hao and GIANNAKIS G B. Exploiting sparse user activity in multiuser detection[J]. IEEE Transactions on Communications, 2011, 59(2): 454–465. doi: 10.1109/TCOMM.2011.121410.090570 WANG Jian and SHIM B. Exact recovery of sparse signals using orthogonal matching pursuit: How many iterations do we need?[J]. IEEE Transactions on Signal Processing, 2016, 64(16): 4194–4202. doi: 10.1109/TSP.2016.2568162 孙娜, 刘继文, 肖东亮. 基于BFGS拟牛顿法的压缩感知SL0重构算法[J]. 电子与信息学报, 2018, 40(10): 2408–2414. doi: 10.11999/JEIT170813SUN Na, LIU Jiwen, and XIAO Dongliang. SL0 reconstruction algorithm for compressive sensing based on BFGS quasi newton method[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2408–2414. doi: 10.11999/JEIT170813 -






 下载:
下载:



 下载:
下载:
