地磁背景下基于传感器阵列的磁偶极子目标跟踪方法

陈路昭; 冯永强; 郭瑞杰; 朱万华; 方广有

doi:10.11999/JEIT190236

地磁背景下基于传感器阵列的磁偶极子目标跟踪方法

doi: 10.11999/JEIT190236

陈路昭^{1, 2, 3},
冯永强^{1, 2},
郭瑞杰³,
朱万华^1, ,,
方广有¹

1.
中国科学院电磁辐射与探测技术重点实验室北京 100190
2.
中国科学院大学北京 100049
3.
北京自动化控制设备研究所北京 100074

基金项目: 国家自然科学基金青年基金(41704177)和国家重点研发计划“深地资源勘查开采”重点专项(2018YFC0603201)

详细信息

作者简介:
陈路昭：男，1992年生，博士，研究方向为传感器阵列的磁信号处理方法、运动平台磁干扰补偿技术

冯永强：男，1985年生，博士生，研究方向为航磁系统硬件设计与航磁数据处理方法

郭瑞杰：女，1992年生，硕士，研究方向为组合导航与系统控制技术

朱万华：男，1982年生，副研究员，主要研究方向为高灵敏度磁场传感器关键技术、高性能磁屏蔽关键技术

方广有：男，1963年生，研究员，主要研究方向为超宽带电磁场理论及工程应用、超宽带雷达成像技术、微波成像新方法和新技术

通讯作者:
朱万华　whzhu@mail.ie.ac.cn

中图分类号: O411.5; TN911.73
计量
- 文章访问数: 3600
- HTML全文浏览量: 1176
- PDF下载量: 129
- 被引次数: 0
出版历程
- 收稿日期: 2019-04-10
- 修回日期: 2019-12-01
- 网络出版日期: 2019-12-09
- 刊出日期: 2020-03-19

Magnetic Dipole Object Tracking Algorithm Based on Magnetometer Array in Geomagnetic Background

Luzhao CHEN^{1, 2, 3},
Yongqiang FENG^{1, 2},
Ruijie GUO³,
Wanhua ZHU^{1
, ,},
Guangyou FANG¹

1.
Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Beijing Automation Control Equipment Institute, Beijing 100074, China

Funds: The Youth Program of National Natural Science Foundation of China (41704177), The National Key R&D Program of China (2018YFC0603201)

摘要

摘要:
针对地磁背景下磁偶极子目标跟踪过程中存在的地磁干扰与模型非线性的问题，该文提出一种基于差量磁异常的蒙特卡洛卡尔曼滤波(MCKF)跟踪方法。新的跟踪方法以传感器阵列测量磁场的差量作为观测信号，并利用蒙特卡洛卡尔曼滤波算法解决模型的非线性问题，实现磁偶极子目标的实时跟踪。通过仿真跟踪实验，结果表明该文算法较传统的扩展或无迹卡尔曼滤波算法在稳定跟踪过程中对目标特征参数的估计更精确；通过地磁背景跟踪实验，结果验证了该文算法较传统算法在低信噪比下的性能优势。
- 磁偶极子 /
- 蒙特卡洛卡尔曼滤波 /
- 传感器阵列 /
- 地磁背景
Abstract:
In order to solve the problem of geomagnetic interference and model nonlinearity in the tracking process of magnetic dipole under geomagnetic background, Monte Carlo Kalman Filter (MCKF) tracking method based on differential magnetic anomaly is proposed in this paper. The new tracking method takes the difference of magnetic field measured by sensor array as the observation signal, and uses Monte Carlo Kalman Filtering (MCKF) algorithm to solve the nonlinear problem of the model to realize the real-time tracking of magnetic dipole targets. The simulation results show that the proposed method is more accurate than the traditional Extended Kalman Filter (EKF) or Untracked Kalman Filter (UKF) in the stable tracking process. The results of real geomagnetic background tracking experiments show that the proposed algorithm has better tracking performance under low SNR.
- Magnetic dipole /
- Monte Carlo Kalman Filter (MCKF) /
- Sensor array /
- Geomagnetic background

HTML全文

图 1 仿真磁偶极子运动轨迹与传感器分布位置

下载: 全尺寸图片幻灯片

图 2 传感器测量结果

下载: 全尺寸图片幻灯片

图 3 基于MCKF跟踪算法的流程图

下载: 全尺寸图片幻灯片

图 4 仿真磁偶极子跟踪结果对比

下载: 全尺寸图片幻灯片

图 5 真实目标跟踪实验

下载: 全尺寸图片幻灯片

图 6 跟踪实验模拟磁性目标体

下载: 全尺寸图片幻灯片

图 7 阵列传感器测量磁场与差量磁场

下载: 全尺寸图片幻灯片

图 8 模拟磁性目标的位置跟踪结果

下载: 全尺寸图片幻灯片

图 9 模拟磁性目标的磁矩跟踪结果

下载: 全尺寸图片幻灯片

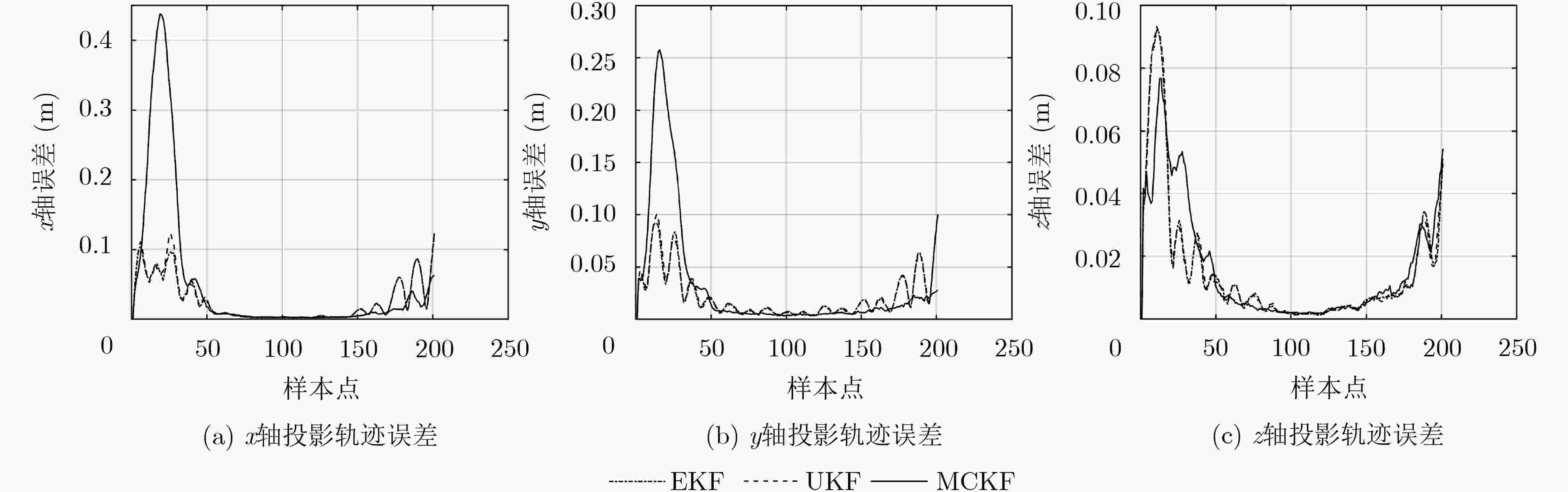
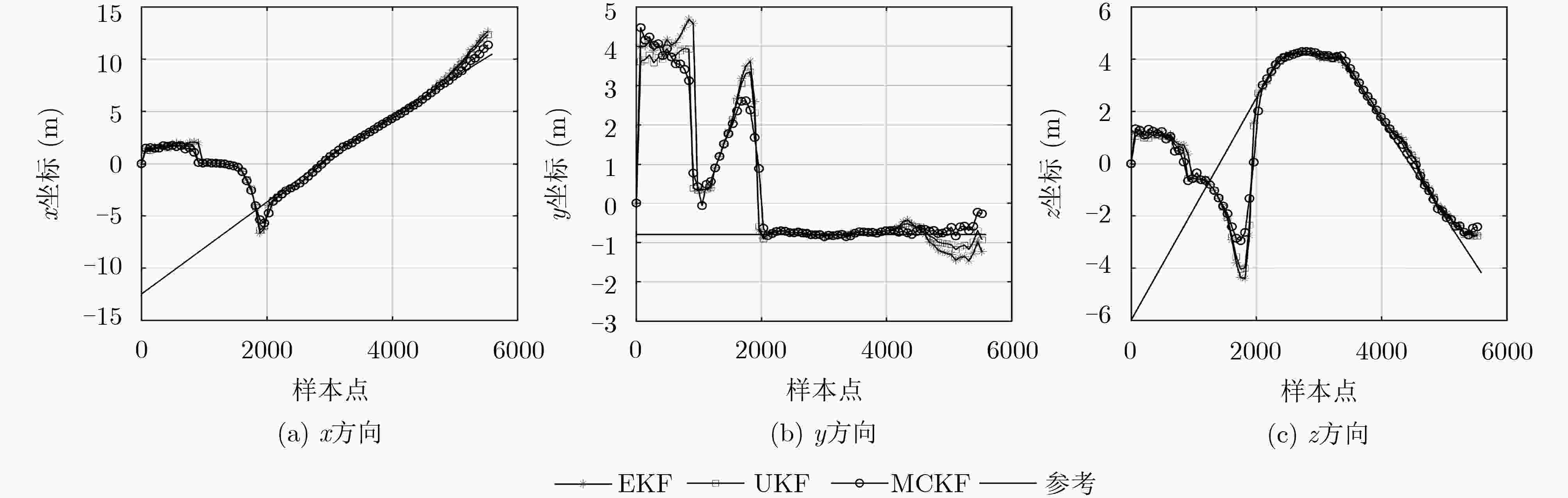
表 1 不同跟踪算法各方向投影轨迹跟踪误差(m)

	跟踪算法	时间区间
	跟踪算法	1～40点	41～80点	81～120点	120～160点	160～200点
x方向	EKF	0.0651	0.0127	0.0023	0.0057	0.0409
	UKF	0.0689	0.0127	0.0024	0.0057	0.0410
	MCKF	0.2143	0.0153	0.0024	0.0039	0.0218
y方向	EKF	0.0491	0.0113	0.0059	0.0100	0.0319
	UKF	0.0512	0.0112	0.0061	0.0096	0.0318
	MCKF	0.1237	0.0115	0.0042	0.0061	0.0158
z方向	EKF	0.0430	0.0089	0.0021	0.0042	0.0163
	UKF	0.0436	0.0088	0.0022	0.0041	0.0164
	MCKF	0.0456	0.0086	0.0022	0.0043	0.0198

下载: 导出CSV

表 2 不同蒙特卡洛样本点数的算法各方向投影轨迹跟踪误差(m)

表2(a) x方向
蒙特卡洛样本点数	时间区间
蒙特卡洛样本点数	1～40	41～80	81～120	120～160	160～200
50	0.2817	0.0242	0.0035	0.0052	0.0264
100	0.2481	0.0194	0.0030	0.0046	0.0231
200	0.2143	0.0153	0.0024	0.0039	0.0218
400	0.2316	0.0159	0.0023	0.0039	0.0212
表2(b) y方向
蒙特卡洛样本点数	时间区间
蒙特卡洛样本点数	1～40	41～80	81～120	120～160	160～200
50	0.1658	0.0168	0.0049	0.0069	0.0192
100	0.1442	0.0141	0.0047	0.0063	0.0166
200	0.1237	0.0115	0.0042	0.0061	0.0158
400	0.1346	0.0118	0.0043	0.0059	0.0151
表2(c) z方向
蒙特卡洛样本点数	时间区间
蒙特卡洛样本点数	1～40	41～80	81～120	120～160	160～200
50	0.0569	0.0124	0.0031	0.0053	0.0242
100	0.0496	0.0105	0.0026	0.0046	0.0202
200	0.0456	0.0086	0.0022	0.0043	0.0198
400	0.0466	0.0090	0.0021	0.0042	0.0195

下载: 导出CSV

参考文献(23)

IOANNIDIS G. Identification of a ship or submarine from its magnetic signature[J]. IEEE Transactions on Aerospace and Electronic Systems, 1977, AES-13(3): 327–329. doi: 10.1109/TAES.1977.308404

FAGGIONI O, SOLDANI M, GABELLONE A, et al. Undersea harbour defence: A new choice in magnetic networks[J]. Journal of Applied Geophysics, 2010, 72(1): 46–56. doi: 10.1016/j.jappgeo.2010.07.001

ZHANG Mengying, WANG Hua, GE Lin, et al. Automatic search algorithms for near-field ferromagnetic targets based on magnetic anomaly detection[J]. Mathematical Problems in Engineering, 2018, 2018: 2130236. doi: 10.1155/2018/2130236

SHEINKER A, LERNER B, SALOMONSKI N, et al. Localization and magnetic moment estimation of a ferromagnetic target by simulated annealing[J]. Measurement Science and Technology, 2007, 18(11): 3451–3457. doi: 10.1088/0957-0233/18/11/027

SHEINKER A, SALOMONSKI N, GINZBURG B, et al. Remote sensing of a magnetic target utilizing population based incremental learning[J]. Sensors and Actuators A: Physical, 2008, 143(2): 215–223. doi: 10.1016/j.sna.2007.10.064

YANG Wan’an, HU Chao, LI Mao, et al. A new tracking system for three magnetic objectives[J]. IEEE Transactions on Magnetics, 2010, 46(12): 4023–4029. doi: 10.1109/tmag.2010.2076823

GAO Xiang, YAN Shenggang, and LI Bi. A novel method of localization for moving objects with an alternating magnetic field[J]. Sensors, 2017, 17(4): 923(1–12). doi: 10.3390/s17040923

WANG Chen, QU Xiaodong, ZHANG Xiaojuan, et al. A fast calibration method for magnetometer array and the application of ferromagnetic target localization[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(7): 1743–1750. doi: 10.1109/TIM.2017.2668558

贾文抖, 林春生, 陈春行, 等. 针对磁目标定位失效的改进欧拉定位方法[J]. 海军工程大学学报, 2018, 30(3): 37–42.

JIA Wendou, LIN Chunsheng, CHEN Chunxing, et al. Improved Euler method for preventing failure of positioning magnetic target[J]. Journal of Naval University of Engineering, 2018, 30(3): 37–42.

WIEGERT R and OESCHGER J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance[C]. The OCEANS 2005 MTS/IEEE, Washington, USA, 2005: 1325–1332.

BIRSAN M. Non-linear Kalman filters for tracking a magnetic dipole[R]. Defence R&D Canada, Atlantic, 2005.

BIRSAN M. Unscented particle filter for tracking a magnetic dipole target[C]. The OCEANS 2005 MTS/IEEE, Washington, USA, 2005, 1656–1659.

KOZICK R J and SADLER B M. Algorithms for tracking with an array of magnetic sensors[C]. The 5th IEEE Sensor Array and Multichannel Signal Processing Workshop, Darmstadt, Germany, 2008: 423–427.

ALHMIEDAT T, ABU TALEB A, and BSOUL M. A study on threads detection and tracking systems for military applications using WSNs[J]. International Journal of Computer Applications, 2012, 40(15): 12–18. doi: 10.5120/5055-7347

张朝阳, 肖昌汉, 高俊吉, 等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报, 2010, 18(5): 862–868. doi: 10.3969/j.issn.1005-0930.2010.05.016

ZHANG Zhaoyang, XIAO Changhan, GAO Junji, et al. Experiment research of magnetic dipole model applicability for a magnetic object[J]. Journal of Basic Science and Engineering, 2010, 18(5): 862–868. doi: 10.3969/j.issn.1005-0930.2010.05.016

于振涛, 吕俊伟, 张本涛. 基于海底磁力仪阵列的磁性目标定位方法[J]. 武汉理工大学学报, 2012, 34(6): 131–135. doi: 10.3963/j.issn.1671-4431.2012.06.028

YU Zhentao, LÜ Junwei, and ZHANG Bentao. A method to localize magnetic target based on a seabed array of magnetometers[J]. Journal of Wuhan University of Technology, 2012, 34(6): 131–135. doi: 10.3963/j.issn.1671-4431.2012.06.028

吴志东, 周穗华, 陈志毅. 基于非线性滤波算法的磁偶极子跟踪[J]. 鱼雷技术, 2013, 21(4): 262–267. doi: 10.3969/j.issn.1673-1948.2013.04.006

WU Zhidong, ZHOU Suihua, and CHEN Zhiyi. Magnetic dipole tracking based on nonlinear filtering algorithm[J]. Torpedo Technology, 2013, 21(4): 262–267. doi: 10.3969/j.issn.1673-1948.2013.04.006

高俊吉, 刘大明, 周国华. 水中非合作运动磁性目标跟踪及参数估计[J]. 哈尔滨工程大学学报, 2013, 34(9): 1124–1130. doi: 10.3969/j.issn.1006-7043.201209033

GAO Junji, LIU Daming, and ZHOU Guohua. Study on the tracking and parameter estimating of unknown moving magnetism objects[J]. Journal of Harbin Engineering University, 2013, 34(9): 1124–1130. doi: 10.3969/j.issn.1006-7043.201209033

张宏欣, 周穗华, 吴志东, 等. 基于改进粗糙化粒子滤波的磁偶极子跟踪[J]. 华中科技大学学报: 自然科学版, 2014, 42(9): 76–80. doi: 10.13245/j.hust.140917

ZHANG Hongxin, ZHOU Suihua, WU Zhidong, et al. Magnetic dipole localization based on improved roughening particle filter[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014, 42(9): 76–80. doi: 10.13245/j.hust.140917

周穗华, 张文成, 张宏欣. 基于混合卡尔曼滤波的磁偶极子目标跟踪[J]. 水雷战与舰船防护, 2015, 23(4): 7–11.

ZHOU Suihua, ZHANG Wencheng, and ZHANG Hongxin. Magnetic dipole target tracking based on mixed kalman filter[J]. Mine Warfare &Ship Self-defence, 2015, 23(4): 7–11.

吴垣甫, 孙跃. 基于递推更新卡尔曼滤波的磁偶极子目标跟踪[J]. 北京航空航天大学学报, 2017, 43(9): 1805–1812. doi: 10.13700/j.bh.1001-5965.2016.0694

WU Yuanfu and SUN Yue. Magnetic dipole target tracking based on recursive update Kalman filter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1805–1812. doi: 10.13700/j.bh.1001-5965.2016.0694

张宏欣, 周穗华, 张伽伟. 磁偶极子跟踪的渐进贝叶斯滤波方法[J]. 自动化学报, 2017, 43(5): 822–834. doi: 10.16383/j.aas.2017.c160052

ZHANG Hongxin, ZHOU Suihua, and ZHANG Jiawei. A progressive bayesian filtering approach to magnetic dipole tracking[J]. Acta Automatica Sinica, 2017, 43(5): 822–834. doi: 10.16383/j.aas.2017.c160052

张宏欣. 磁性目标跟踪的多模型自适应滤波方法[J]. 数字海洋与水下攻防, 2018, 1(2): 57–62.

ZHANG Hongxin. Multiple-model adaptive filtering method for magnetic target tracking[J]. Digital Ocean &Underwater Warfare, 2018, 1(2): 57–62.

施引文献

资源附件(0)

访问统计