Neighbor Information Constrained Node Scheduling in Stochastic Heterogeneous Wireless Sensor Networks
-
摘要: 针对高密度部署的随机异构传感器网络内部存在的覆盖冗余问题,该文提出一种随机异构无线传感器网络的节点调度算法(NSSH)。在网络原型拓扑的支撑下构建Delaunary三角剖分,规划出节点进行本地化调度的局部工作子集。通过折中与邻近节点的空外接圆半径,完成对感知半径的独立配置;引入几何线、面概念,利用重叠面积和有效约束圆弧完成对灰、黑色节点的分类识别,使得节点仅依赖本地及邻居信息进行半径调整和冗余休眠。仿真结果表明,NSSH能以低复杂度的代价,近似追平贪婪算法的去冗余性能,并表现出了对网络规模、异构跨度和参数配置的低敏感性。Abstract: Considering coverage redundancy problem existed in random heterogeneous sensor networks with high density deployment, a Node Scheduling algorithm for Stochastic Heterogeneous wireless sensor networks(NSSH) is proposed. The Delaunary triangulation is constructed based on the network prototype topology to work out a local subset of nodes for localization scheduling. Independent configuration of the perceived radius is achieved by discounting the radius of the circumcircle with the adjacent node. The concept of geometric line and plane is introduced, and the overlapping area and the effective constrained arcs are used to classify and identify the grey and black nodes. So the node only relies on local and neighbor information for radius adjustment and redundant node sleep. The simulation results show that NSSH can approximately match the dropping redundancy of greedy algorithm at the cost of low complexity, and exhibit low sensitivity to network size, heterogeneous span and parameter configuration.
-
Key words:
- Sensor network /
- Stochastic heterogeneous /
- Coverage /
- Node scheduling /
- Neighbor information
-
表 1 半径调整算法步骤
半径调整算法(${T^i},{r_i}$) (1) $r_{\rm c}^i = \varnothing $ (2) for $p = 1:P$ (3) calculate the radius $r_{{\rm{cp}}}^i$ of ${T_p}^i$//计算空外接圆半径 (4) $r_{\rm c}^i = r_{\rm c}^i \cup r_{ {\rm{cp} } }^i$ (5) end for (6 ${r_i} = \min ({r_i},\max \left( {r_{\rm c}^i} \right))$//若$\max \left( {r_{\rm c}^i} \right) > {r_i}$,则保留原${r_i}$ (7) return (${r_i}$) 表 2 NSSH算法步骤
NSSH (${T^i}$,${r_i}$,${\rm{N}}{{\rm{e}}_i}$,${\theta _{{\rm{th}}}}$,${\left| {{\rm{arc}}} \right|_{{\rm{th}}}}$,$k$) (1) 初始化:${\rm{s}}{{\rm{t}}_i} = 1$, ${\stackrel \frown {{\rm{ar}}{{\rm{c}}_i}}}=\varnothing$ (2) ${r_i}$=半径调整算法(${T^i},{r_i}$) (3) for $q = 1:Q$ (4) ${\rm{if}}({\theta _{i,jq}} > {\theta _{{\rm{th}}}})$) //基于定义5和式(1)判定灰色节点 (5) ${\rm{s}}{{\rm{t}}_i} = 0$ (6) end if (7) ${\stackrel \frown {{\rm{ar}}{{\rm{c}}_i}}}={\stackrel \frown {{\rm{ar}}{{\rm{c}}_i}}} \cup {\stackrel \frown {{\rm{ar}}{{\rm{c}}_{i\_jq}}}}$ //计算有效约束圆弧 (8) end for (9) calculate $\left| {{\rm{ar}}{{\rm{c}}_i}} \right|$ ${k_i}$ //基于式(2)—式(4)计算有效约束圆弧度
数,统计${s_i}$的覆盖度${k_i}$(10) if ($\left| {{\rm{ar}}{{\rm{c}}_i}} \right| \ge {\left| {{\rm{arc}}} \right|_{{\rm{th}}}}{\rm{\& \& }}{k_i} \ge k$)//基于定义6判定黑色节点 (11) ${\rm{s}}{{\rm{t}}_i} = 0$ (12) end if (13) return (${\rm{s}}{{\rm{t}}_i}$) 表 3 5种算法参数
算法 节点数目 $N = {\rm{100}}$, $N = {\rm{150}}$ $N = {\rm{200}}$, $N = {\rm{250}}$ $N = {\rm{300}}$, $N = {\rm{350}}$ $N = {\rm{400}}$, $N = {\rm{450}}$ $N = {\rm{500}}$ NSSH ${\theta _{{\rm{th}}}} = 0.82$ ${\left| {{\rm{arc}}} \right|_{{\rm{th}}}} = 1.96{\text{π}} $ $k{\rm{ = 2}}$ GGA $\mu {\rm{ = 0}}{\rm{.9}}$ MCLC $\Delta c < 0.05$ COAN ${r_{{\rm{thr}}}} = 4.4$
${\eta _{{\rm{thr}}}} = 1.87{\text{π}} $
${m_{{\rm{thr}}}} = 11$
$k = 1$${r_{{\rm{thr}}}} = 4.6$
${\eta _{{\rm{thr}}}} = 1.9{\text{π}} $
${m_{{\rm{thr}}}} = 12$
$k = 1$${r_{{\rm{thr}}}} = 4.8$
${\eta _{{\rm{thr}}}} = 1.93{\text{π}}$
${m_{t{\rm{hr}}}} = 13$
$k = 1$${r_{{\rm{thr}}}} = 5.2$
${\eta _{{\rm{thr}}}} = 1.96{\text{π}} $
${m_{{\rm{thr}}}} = 13$
$k = 1$${r_{{\rm{thr}}}} = 5.4$
${\eta _{{\rm{thr}}}} = 1.98{\text{π}} $
${m_{{\rm{thr}}}} = 15$
$k = 1$NDBS ${k_2}({r_1}/{r_2}) = 4$
${k_2}({r_2}/{r_1}) = 7$
${k_3}({r_1}/{r_2}) = 7$
${k_3}({r_2}/{r_1}) = 16$${k_2}({r_1}/{r_2}) = 4$
${k_2}({r_2}/{r_1}) = 8$
${k_3}({r_1}/{r_2}) = 8$
${k_3}({r_2}/{r_1}) = 16$${k_2}({r_1}/{r_2}) = 4$
${k_2}({r_2}/{r_1}) = 7$
${k_3}({r_1}/{r_2}) = 8$
${k_3}({r_2}/{r_1}){\rm{ = 15}}$${k_2}({r_1}/{r_2}) = 3$
${k_2}({r_2}/{r_1}) = 6$
${k_3}({r_1}/{r_2}) = 7$
${k_3}({r_2}/{r_1}) = 14$${k_2}({r_1}/{r_2}) = 3$
${k_2}({r_2}/{r_1}) = 6$
${k_3}({r_1}/{r_2}) = 6$
${k_3}({r_2}/{r_1}) = 13$注:表中参数$\Delta c$代表MCLC算法覆盖子集的约束条件,${r_{{\rm{thr}}}}$, ${\eta _{{\rm{thr}}}}$, ${m_{{\rm{thr}}}}$仅针对COAN算法,${k_2}({r_1}/{r_2})$, ${k_2}({r_2}/{r_1})$, ${k_3}({r_1}/{r_2})$, ${k_3}({r_2}/{r_1})$仅针对NDBS算法,具体参数解释可查阅文献[8,9]。 -
SLIJEPCEVIC S and POTKONJAK M. Power efficient organization of wireless sensor networks[C]. Conference Record IEEE International Conference on Communications, Helsinki, Finland, 2001: 472–476. 付寅飞, 熊庆旭. 综合路由的无线传感器网络覆盖调度[J]. 北京航空航天大学学报, 2011, 37(7): 801–804, 838. doi: 10.13700/j.bh.1001-5965.2011.07.004FU Yinfei and XIONG Qingxu. Coverage-scheduling integrated routing in wireless sensor networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(7): 801–804, 838. doi: 10.13700/j.bh.1001-5965.2011.07.004 韩志杰, 吴志斌, 王汝传, 等. 新的无线传感器网络覆盖控制算法[J]. 通信学报, 2011, 32(10): 174–184. doi: 10.3969/j.issn.1000-436X.2011.10.022HAN Zhijie, WU Zhibin, WANG Ruchuan, et al. Novel coverage control algorithm for wireless sensor network[J]. Journal on Communications, 2011, 32(10): 174–184. doi: 10.3969/j.issn.1000-436X.2011.10.022 党小超, 邵晨光, 郝占军. 半径可调的无线传感器网络三维覆盖算法[J]. 计算机应用, 2018, 38(9): 2581–2586, 2615. doi: 10.11772/j.issn.1001-9081.2018020357DANG Xiaochao, SHAO Chenguang, and HAO Zhanjun. 3D-coverage algorithm based on adjustable radius in wireless sensor network[J]. Journal of Computer Applications, 2018, 38(9): 2581–2586, 2615. doi: 10.11772/j.issn.1001-9081.2018020357 BHATTACHARJEE M and GUPTA S. Determining redundant nodes in a location unaware wireless sensor network[C]. IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 2014: 858–862. CHENAIT M, ZEBBANE B, FILALI S, et al. A low-complex coverage eligibility algorithm for wireless sensor networks[C]. International Conference on Intelligent Information Processing, Security and Advanced Communication, Batna, Algeria, 2015: Article No.85. doi: 10.1145/2816839.2816854. CHENAIT M, ZEBBANE B, and BADACHE N. A new k-coverage model to determine redundant sensors in wireless sensor networks[C]. 2018 International Conference on Smart Communications in Network Technologies (SaCoNeT), El Oued, Algeria, 2018: 149–154. 刘浩然, 赵赫瑶, 邓玉静, 等. 基于非合作博弈的无线传感器网络覆盖控制算法[J]. 通信学报, 2019, 40(1): 71–78. doi: 10.11959/j.issn.1000-436x.2019006LIU Haoran, ZHAO Heyao, DENG Yujing, et al. Coverage control algorithm for wireless sensor networks based on non-cooperative game[J]. Journal on Communications, 2019, 40(1): 71–78. doi: 10.11959/j.issn.1000-436x.2019006 贾明伟, 吴敏, 沙超, 等. 节点相邻关系的传感网覆盖优化方法[J]. 电子测量与仪器学报, 2015, 29(11): 1574–1583. doi: 10.13382/j.jemi.2015.11.002JIA Mingwei, WU Min, SHA Chao, et al. Coverage optimization algorithm based on adjacent neighbors for sensor networks[J]. Journal of Electronic Measurement and Instrumentation, 2015, 29(11): 1574–1583. doi: 10.13382/j.jemi.2015.11.002 孙力娟, 魏静, 郭剑, 等. 面向异构无线传感器网络的节点调度算法[J]. 电子学报, 2014, 42(10): 1907–1912. doi: 10.3969/j.issn.0372-2112.2014.10.006SUN Lijuan, WEI Jing, GUO Jian, et al. Node scheduling algorithm for heterogeneous wireless sensor networks[J]. Acta Electronica Sinica, 2014, 42(10): 1907–1912. doi: 10.3969/j.issn.0372-2112.2014.10.006 高洁, 吴延红, 白建侠, 等. 无线传感器网络最小覆盖能量优化算法[J]. 传感技术学报, 2016, 29(9): 1435–1440. doi: 10.3969/j.issn.1004-1699.2016.09.024GAO Jie, WU Yanhong, BAI Jianxia, et al. The minimum coverage energy optimization algorithms in wireless sensor network[J]. Chinese Journal of Sensors and Actuators, 2016, 29(9): 1435–1440. doi: 10.3969/j.issn.1004-1699.2016.09.024 权恩猛, 吴斌. 基于Delaunay三角剖分的有向传感器网络覆盖增强算法[J]. 计算机应用研究, 2018, 35(8): 2447–2449. doi: 10.3969/j.issn.1001-3695.2018.08.052QUAN Enmeng and WU Bin. Coverage enhancement algorithm based on delaunay triangulation for directional sensor networks[J]. Application Research of Computers, 2018, 35(8): 2447–2449. doi: 10.3969/j.issn.1001-3695.2018.08.052 杜晓玉, 孙力娟, 郭剑, 等. 异构无线传感器网络覆盖优化算法[J]. 电子与信息学报, 2014, 36(3): 696–702. doi: 10.3724/SP.J.1146.2013.00730DU Xiaoyu, SUN Lijuan, GUO Jian, et al. Coverage optimization algorithm for heterogeneous WSNs[J]. Journal of Electronics &Information Technology, 2014, 36(3): 696–702. doi: 10.3724/SP.J.1146.2013.00730 刁鹏飞, 王艳娇. 基于节点休眠的水下无线传感器网络覆盖保持分簇算法[J]. 电子与信息学报, 2018, 40(5): 1101–1107. doi: 10.11999/JEIT170787DIAO Pengfei and WANG Yanjiao. Coverage-preserving clustering algorithm for underwater sensor networks based on the sleeping mechanism[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1101–1107. doi: 10.11999/JEIT170787 LI Wei and ZHANG Wei. Coverage hole and boundary nodes detection in wireless sensor networks[J]. Journal of Network and Computer Applications, 2015, 48: 35–48. doi: 10.1016/j.jnca.2014.10.011. -







 下载:
下载:




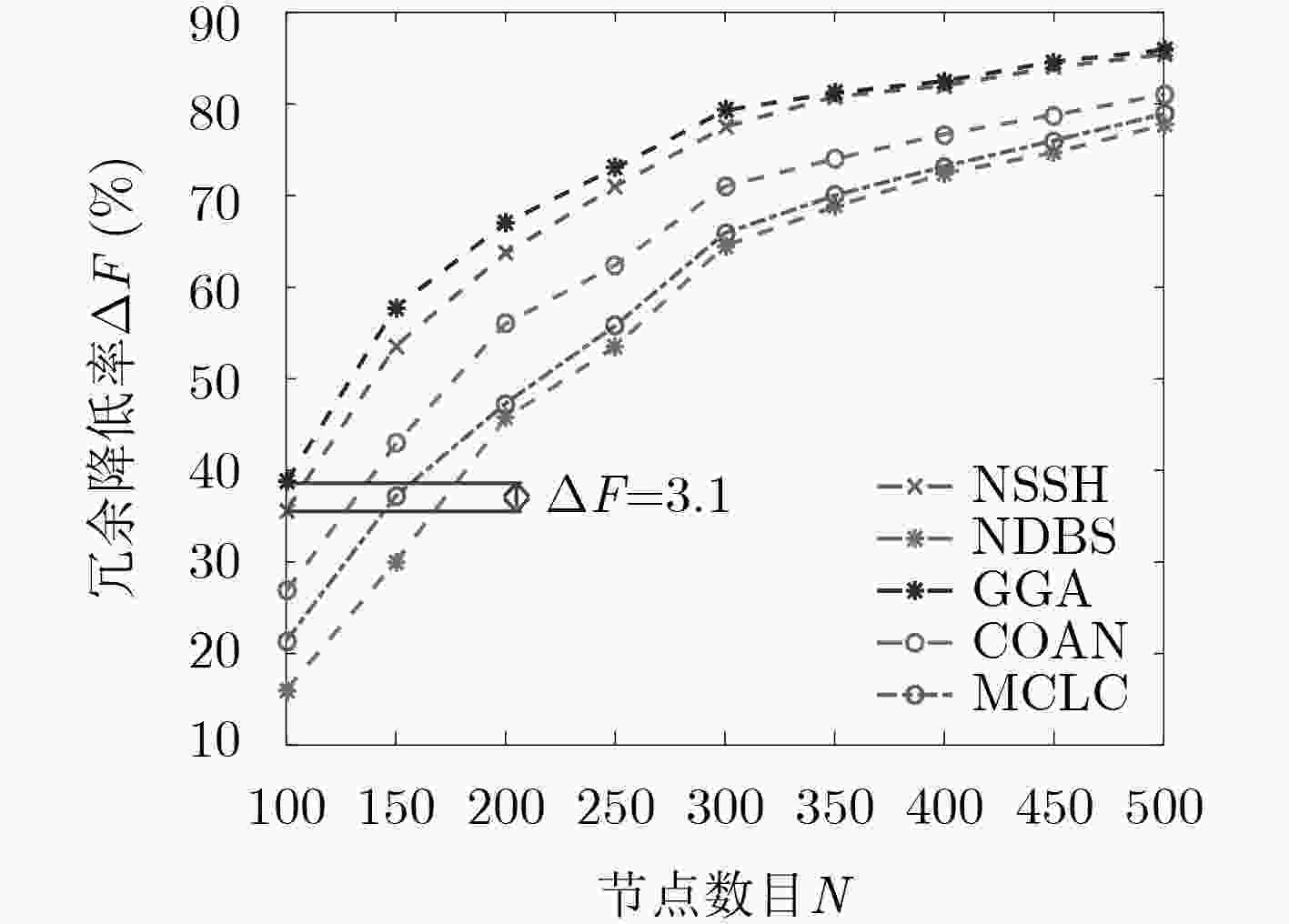

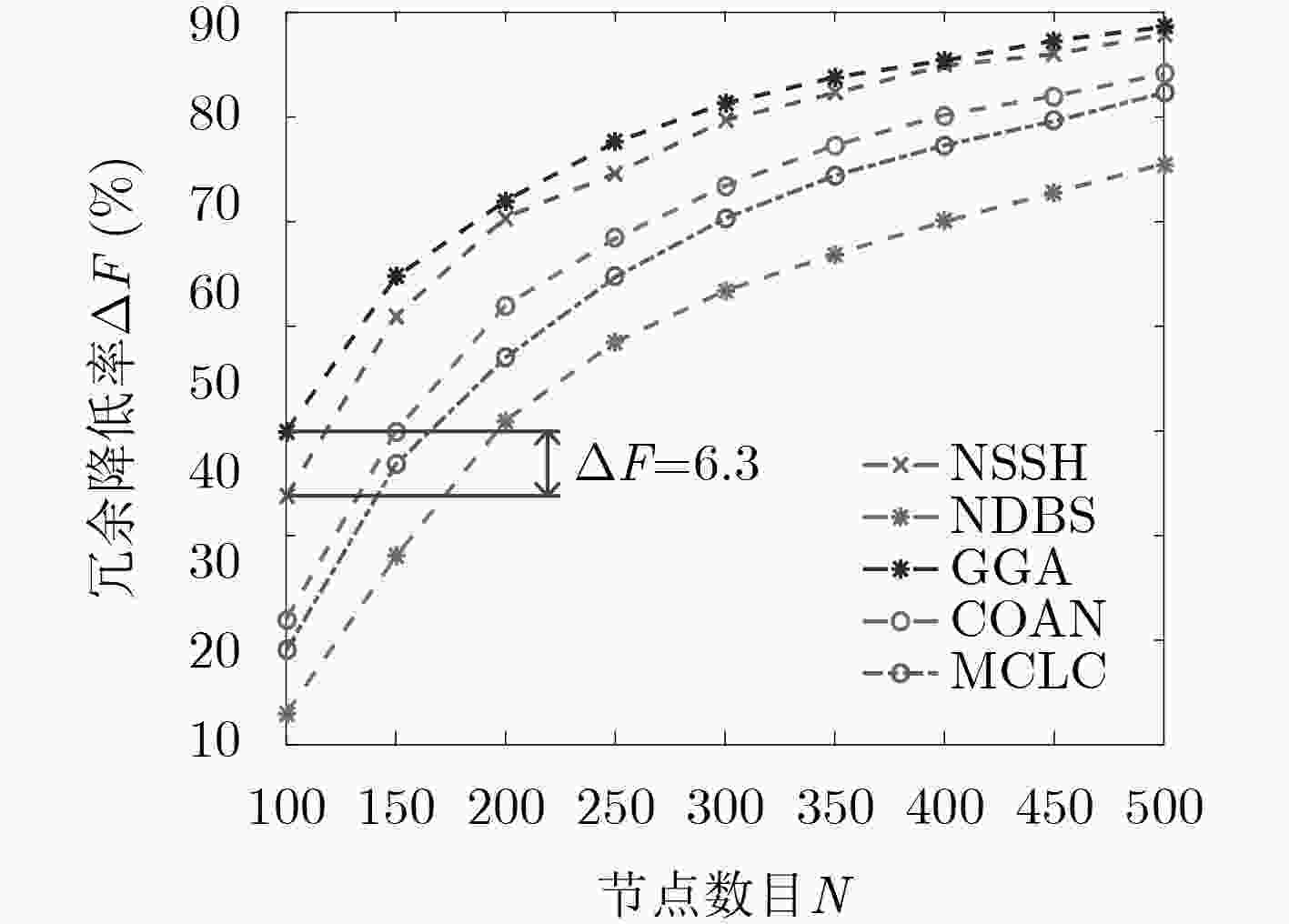



 下载:
下载:
