Joint Design of Quasi-cyclic Low Density Parity Check Codes and Performance Analysis of Multi-source Multi-relay Coded Cooperative System
-
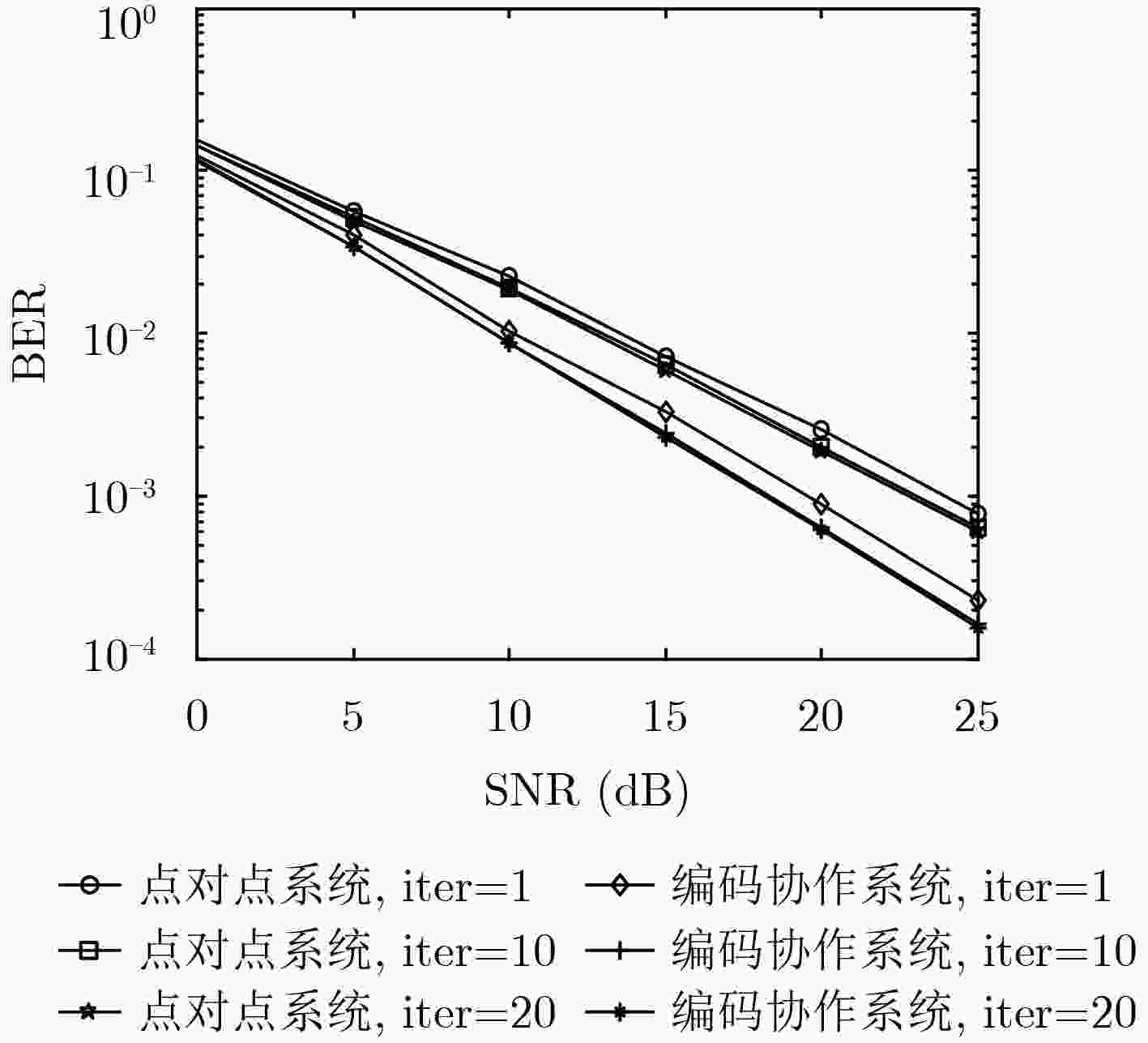
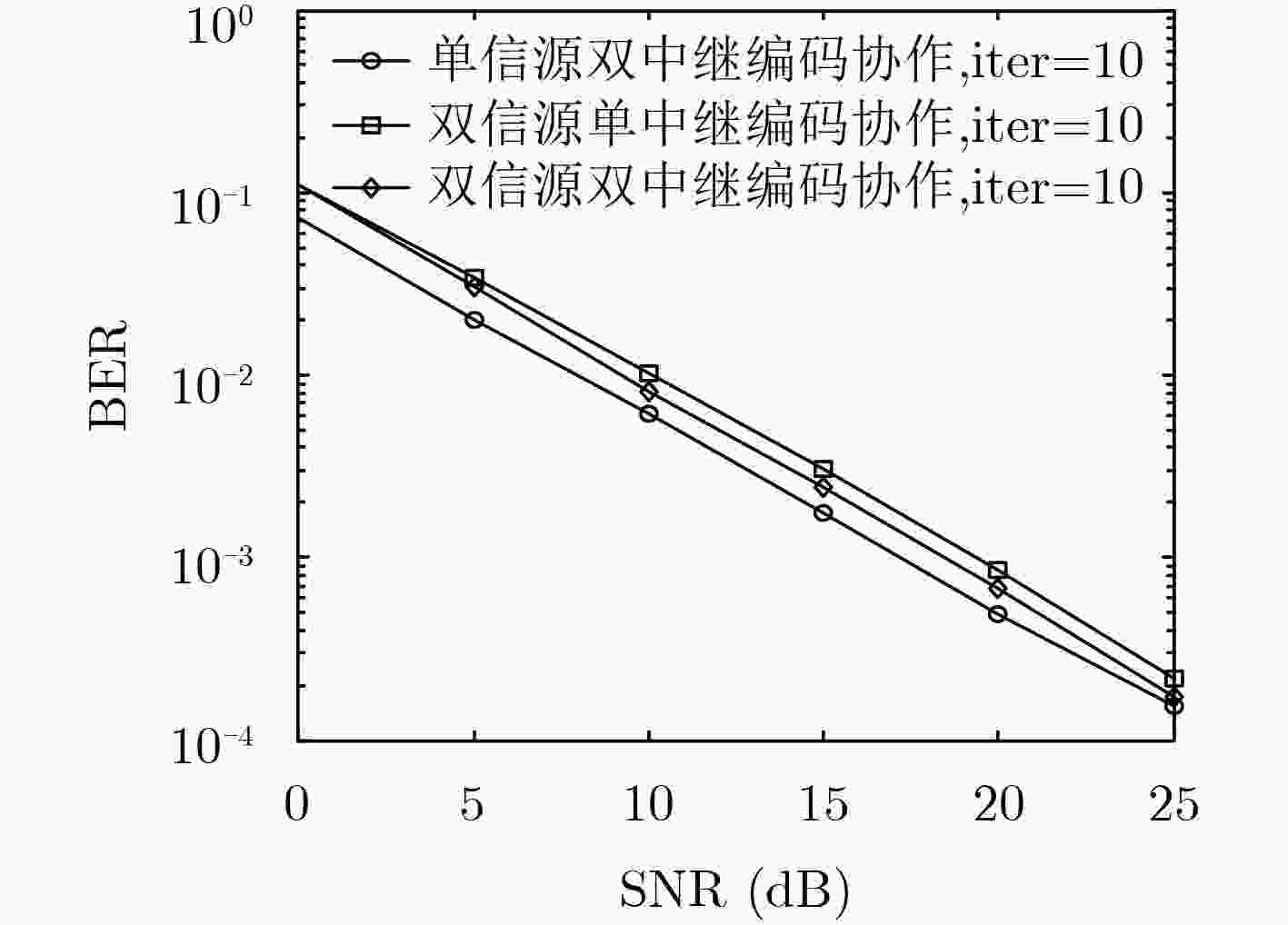
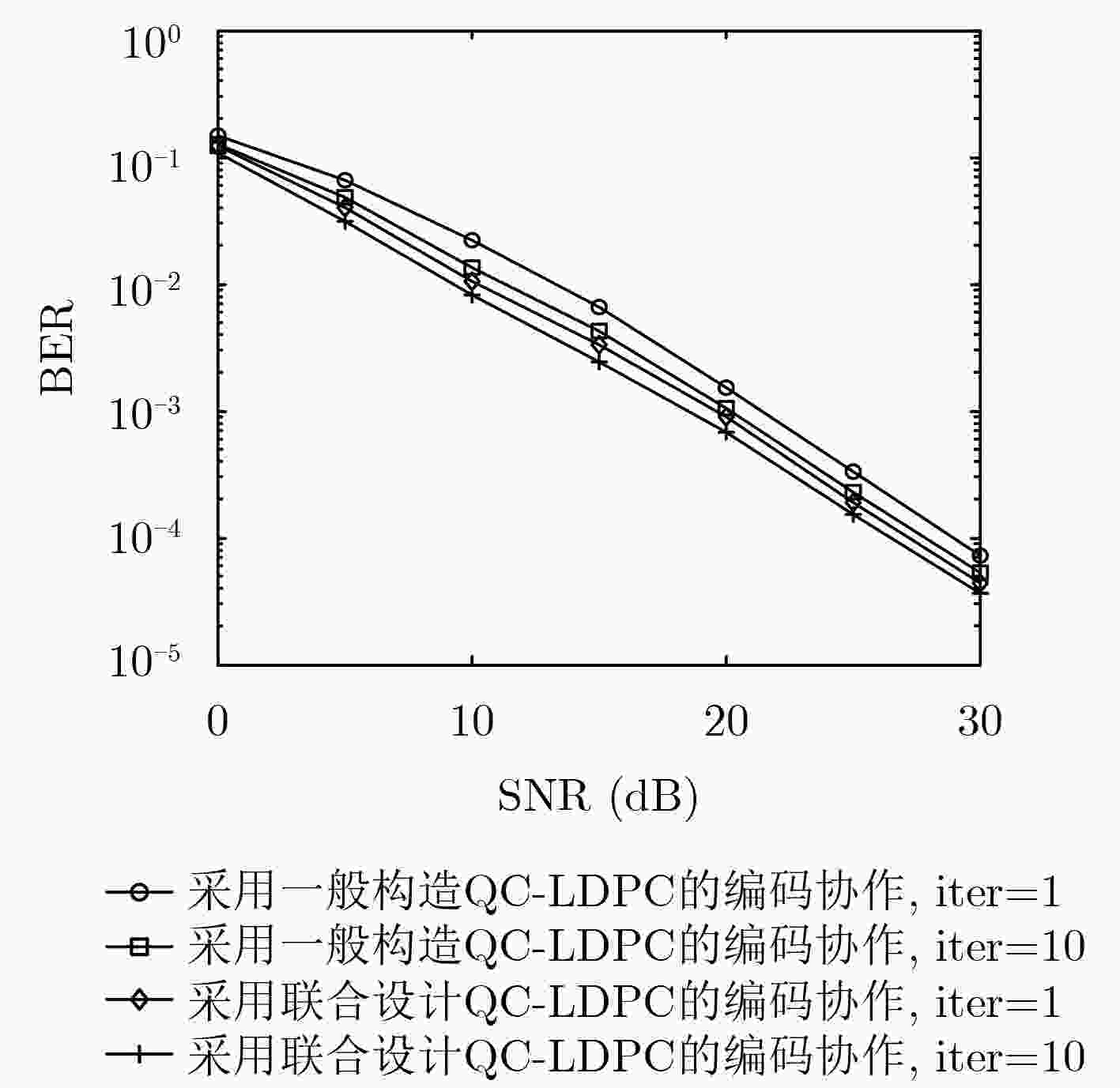
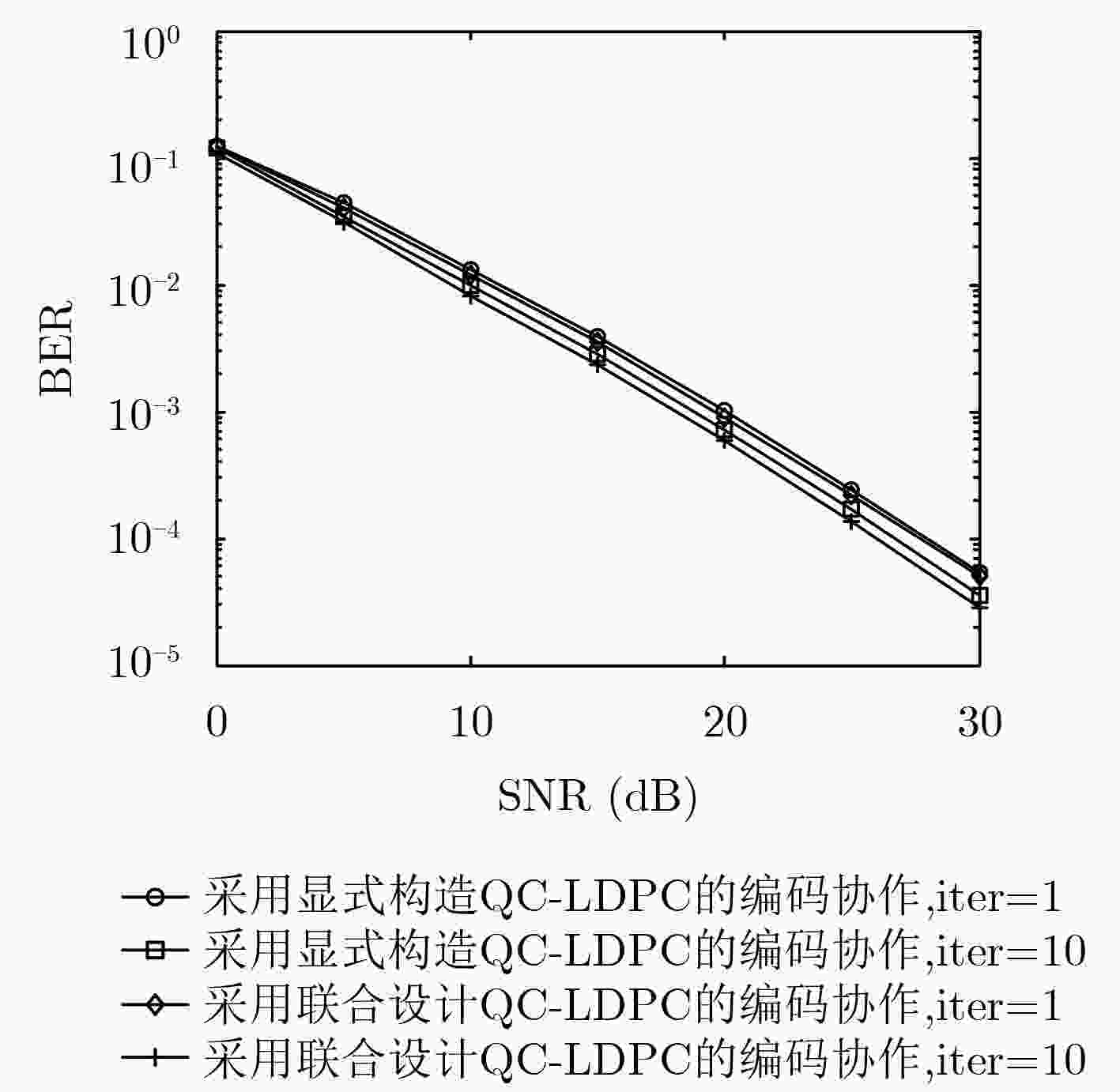
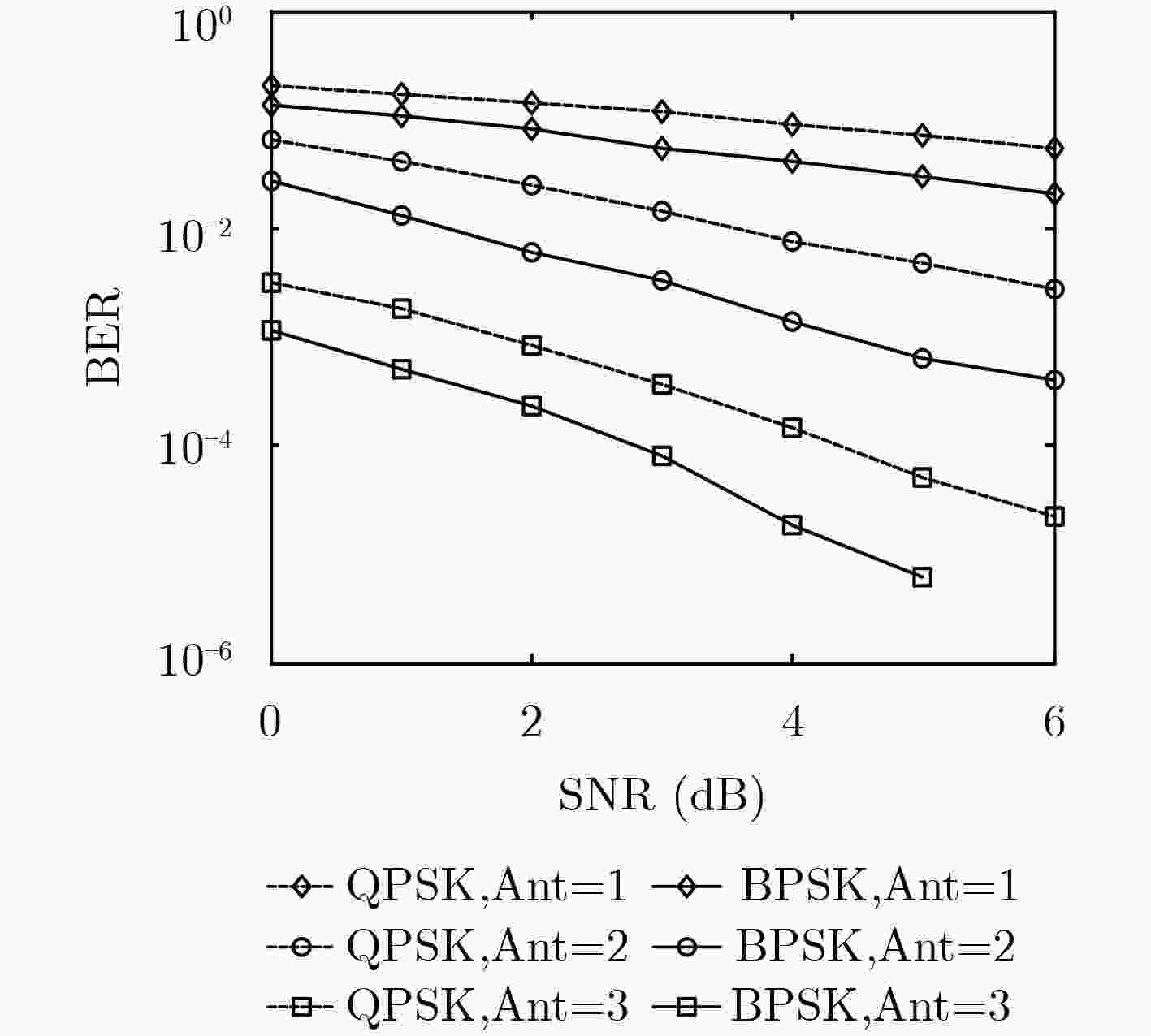
摘要: 为解决多信源多中继低密度奇偶校验(LDPC)码编码协作系统编码复杂度高、编码时延长的问题,该文引入一种特殊结构的LDPC码—基于生成矩阵的准循环LDPC码(QC-LDPC)码。该类码结合了QC-LDPC码与基于生成矩阵LDPC (G-LDPC)码的特点,可直接实现完全并行编码,极大地降低了中继节点的编码时延及编码复杂度。在此基础上,推导出对应于信源节点和中继节点采用的QC-LDPC码的联合校验矩阵,并基于最大公约数(GCD)定理联合设计该矩阵以消除其所有围长为4, 6(girth-4, girth-6)的短环。理论分析和仿真结果表明,在同等条件下该系统的误码率(BER)性能优于相应的点对点系统。仿真结果还表明,与采用显式算法构造QC-LDPC码或一般构造QC-LDPC码的协作系统相比,采用联合设计QC-LDPC码的系统均可获得更高的编码增益。
-
关键词:
- 准循环低密度奇偶校验码 /
- 编码协作 /
- 联合校验矩阵 /
- 最大公约数定理
Abstract: To solve the problems of high encoding complexity and long encoding delay in the multi-source multi-relay Low Density Parity Check (LDPC) coded cooperative system, a special kind of structured LDPC codes—Quasi-Cyclic LDPC (QC-LDPC) codes based on generator matrix is proposed, which combines the characteristics of QC-LDPC codes and Generator-matrix-based LDPC (G-LDPC) codes. It can perform completely parallel encoding, which greatly reduces the encoding complexity and delay at the relays. Based on this, a joint parity check matrix corresponding to the QC-LDPC codes adopted by the sources and relays is deduced, and the matrix is further jointly designed based on the Greatest Common Divisor (GCD) theorem to eliminate all cycles of girth-4 and girth-6. Theoretical analysis and simulation results show that under the same conditions, the Bit Error Rate (BER) performance of the proposed system is better than that of the corresponding point-to-point system. The simulation results also show that the cooperative system with jointly designed QC-LDPC codes can obtain a higher coding gain than the system with explicitly constructed QC-LDPC codes or generally constructed QC-LDPC codes. -
表 1 双信源双中继编码协作及对应点对点系统所采用的QC-LDPC码
信源节点所采用的QC-LDPC码 中继节点所采用的QC-LDPC码 双信源双中继系统 $ {{\text{H}}_{{S_{1}}}} = {{\text{H}}_{1(1100 \times 2200)}} $ $ {{\text{H}}_{{R_{1}}}} = [ {{{\text{A}}_{1(1100 \times 2200)}}}\quad {{{\text{B}}_{1(1100 \times 2200)}}}\quad {\text{I}}_{(1100 \times 1100)}]$ ${{\text{H}}_{{S_{2}}}} = {{\text{H}}_{2(1100 \times 2200)}}$ $ {{\text{H}}_{{R_{2}}}} = [ {{{\text{A}}_{2(1100 \times 2200)}}}\quad {{{\text{B}}_{2(1100 \times 2200)}}}\quad {\text{I}}_{(1100 \times 1100)}] $ Rate=1/2 Rate=4/5 点对点系统 ${{\text{H}}_S} = {{\text{H}}_{(2200 \times 6600)}}$
Rate=1/3\ 表 2 不同信源节点、中继节点数目情况下编码协作系统所采用的QC-LDPC码
信源节点所采用的QC-LDPC码 中继节点所采用的QC-LDPC码 双信源双中继 $ {{\text{H}}_{{S_{1}}}} = {{\text{H}}_{1(1100 \times 2200)}} $ $ { {\text{H} }_{ {R_{1} } } } = [\begin{array}{*{20}{c} } { { {\text{A} }_{1(1100 \times 2200)} } } & { { {\text{B} }_{1(1100 \times 2200)} } } & {\text{I} }_{(1100 \times 1100)} \end{array}] $ $ {{\text{H}}_{{S_{2}}}} = {{\text{H}}_{2(1100 \times 2200)}} $ $ { {\text{H} }_{ {R_{2} } } } = [\begin{array}{*{20}{c} } { { {\text{A} }_{2(1100 \times 2200)} } } & { { {\text{B} }_{2(1100 \times 2200)} } } & {\text{I}_{(1100 \times 1100)} } \end{array} ]$ Rate=1/2 Rate=4/5 双信源单中继 $ {{\text{H}}_{{S_{1}}}} = {{\text{H}}_{1(1100 \times 2200)}} $ ${ {\text{H} }_R} = [\begin{array}{*{20}{c} } { { {\text{A} }_{(1100 \times 2200)} } } & { { {\text{B} }_{(1100 \times 2200)} } } & {{\text{I}}_{(1100 \times 1100)} } \end{array} ]$ $ {{\text{H}}_{{S_{2}}}} = {{\text{H}}_{2(1100 \times 2200)}} $ Rate=1/2 Rate=4/5 单信源双中继 ${{\text{H}}_S} = {{\text{H}}_{1(1100 \times 2200)}}$ $\begin{gathered} {{\text{H}}_{{R_{1}}}} = [\begin{array}{*{20}{c}} {{{\text{A}}_{1(1100 \times 2200)}}}&{{{\text{I}}_{(1100 \times 1100)}}} \end{array}] \\ {{\text{H}}_{{R_{2}}}} = [\begin{array}{*{20}{c}} {{{\text{A}}_{2(1100 \times 2200)}}}&{{{\text{I}}_{(1100 \times 1100)}}} \end{array}] \\ \end{gathered} $ Rate=1/2 Rate=2/3 表 3 采用一般构造QC-LDPC码的协作系统各节点所采用的码字
信源节点所采用的QC-LDPC码 中继节点所采用的QC-LDPC码 双信源双中继 ${d_{\rm v}} = 2$, ${d_{\rm c}} = 4$
B=550${d_{\rm v}} = 2$, ${d_{\rm c}} = 10$
B=550注:dv指每列“1”的个数,dc指每行“1”的个数 表 4 采用显式构造QC-LDPC码的协作系统所采用的码字
信源节点所采用的QC-LDPC码 中继节点所采用的QC-LDPC码 双信源双中继 ${d_{\rm v}} = 2$, ${d_{\rm c}} = 3$
B=730${d_{\rm v}} = 2$, ${d_{\rm c}} = 8$
B=730 -
RYAN W E and LIN Shu. Channel Codes: Classical and Modern[M]. Cambridge: Cambridge University Press, 2009: 201–254. DEHGHAN A and BANIHASHEMI A H. On the tanner graph cycle distribution of random LDPC, random protograph-based LDPC, and random quasi-cyclic LDPC code ensembles[J]. IEEE Transactions on Information Theory, 2018, 64(6): 4438–4451. doi: 10.1109/TIT.2018.2805906 贺文武, 夏巧桥, 邹炼. 基于变量节点更新的交替方向乘子法LDPC惩罚译码算法[J]. 电子与信息学报, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358HE Wenwu, XIA Qiaoqiao, and ZOU Lian. Alternating direction method of multipliers LDPC penalized decoding algorithm based on variable node update[J]. Journal of Electronics &Information Technology, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358 LIU Yuanhua, NIU Xinliang, WANG Xinmei, et al. Design of quasi-cyclic LDPC codes based on Euclidean geometries[J]. Journal of Electronics(China) , 2010, 27(3): 340–344. doi: 10.1007/s11767-010-0348-0 KARIMI M and BANIHASHEMI A H. Counting short cycles of quasi cyclic protograph LDPC codes[J]. IEEE Communications Letters, 2012, 16(3): 400–403. doi: 10.1109/lcomm.2012.020212.112311 JIANG Xueqin and LEE M H. Large girth quasi-cyclic LDPC codes based on the Chinese remainder theorem[J]. IEEE Communications Letters, 2009, 13(5): 342–344. doi: 10.1109/lcomm.2009.082115 袁建国, 梁梦琪, 尚晓娟. 基于Fibonacci数列对QC-LDPC码的一种新颖构造方法[J]. 激光杂志, 2016, 37(6): 37–40. doi: 10.14016/j.cnki.jgzz.2016.06.037YUAN Jianguo, LIANG Mengqi, and SHANG Xiaojuan. A novel construction method of QC-LDPC codes based on Fibonacci sequence[J]. Laser Journal, 2016, 37(6): 37–40. doi: 10.14016/j.cnki.jgzz.2016.06.037 ESMAEILI M and GHOLAMI M. Maximum-girth slope-based quasi-cyclic (2, k≥5) low-density parity-check codes[J]. IET Communications, 2008, 2(10): 1251–1262. doi: 10.1049/iet-com:20080013 VAN NGUYEN B, JUNG H, and KIM K. Physical layer security schemes for full-duplex cooperative systems: State of the art and beyond[J]. IEEE Communications Magazine, 2018, 56(11): 131–137. doi: 10.1109/MCOM.2017.1700588 BANNOUR A, SACCHI C, and SUN Yichuang. MIMO-OFDM based energy harvesting cooperative communications using coalitional game algorithm[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 11166–11179. doi: 10.1109/TVT.2017.2768622 WANG Jieling, YU Quan, LI Zan, et al. Distributed space time block transmission and QRD based diversity detector in asynchronous cooperative communications systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5111–5125. doi: 10.1109/TVT.2018.2812901 ZHANG Shunwai, YANG Fengfan, and SONG Rongfang. Energy-harvesting-based RA-coded cooperative MIMO: Codes design and performance analysis[J]. Digital Signal Processing, 2017, 60(2): 56–62. doi: 10.1016/j.dsp.2016.08.013 MUGHAL S, YANG Fengfan, and UMAR R. Reed-Muller network coded-cooperation with joint decoding[J]. IEEE Communications Letters, 2019, 23(1): 24–27. doi: 10.1109/LCOMM.2018.2879101 陈紫强, 欧阳缮, 肖海林. 解码前传半双工中继信道下协作LDPC 码设计[J]. 电子与信息学报, 2011, 33(11): 2610–2615. doi: 10.3724/SP.J.1146.2011.00323CHEN Ziqiang, OUYANG Shan, and XIAO Hailin. Cooperative LDPC codes design for decode-and-forward half-duplex relay channels[J]. Journal of Electronics &Information Technology, 2011, 33(11): 2610–2615. doi: 10.3724/SP.J.1146.2011.00323 JANANI M, HEDAYAT A, HUNTER T E, et al. Coded cooperation in wireless communications: Space-time transmission and iterative decoding[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 362–371. doi: 10.1109/TSP.2003.821100 LI Zongyan, PENG Mugen, WU Zhanji, et al. Network coding scheme based on LDPC product codes in multiple-access relay system[C]. 2011 IEEE International Conference on Communications Workshops, Kyoto, Japan, 2011: 1–4. ZHANG Shunwai, YANG Fengfan, TANG Lei, et al. Joint design of QC-LDPC codes for coded cooperation system with joint iterative decoding[J]. International Journal of Electronics, 2016, 103(3): 384–405. doi: 10.1080/00207217.2015.1036374 DU Bing and ZHANG Jun. Parity check network coding for wireless cooperative communications[J]. Chinese Journal of Electronics, 2010, 19(2): 339–344. 张顺外. LDPC编码协作系统性能与码的设计研究[D]. [博士论文], 南京航空航天大学, 2013.ZHANG Shunwai. LDPC-coded cooperation: Performance studies and codes design[D]. [Ph.D. dissertation], Nanjing University of Aeronautics and Astronautics, 2013. ZHANG Shunwai, YANG Fengfan, and TANG Lei. Network-coding-based multisource multirelay LDPC-coded cooperative MIMO[J]. Transactions on Emerging Telecommunications Technologies, 2015, 26(3): 491–502. doi: 10.1002/ett.2659 ZHANG Guohua, SUN Rong, and WANG Xinmei. Construction of girth-eight QC-LDPC codes from greatest common divisor[J]. IEEE Communications Letters, 2013, 17(2): 369–372. doi: 10.1109/LCOMM.2012.122012.122292 ZHANG Jianhua and ZHANG Guohua. Deterministic girth-eight QC-LDPC codes with large column weight[J]. IEEE Communications Letters, 2014, 18(4): 656–659. doi: 10.1109/lcomm.2014.030114.132853 张国华, 陈超, 杨洋, 等. Girth-8 (3,L)-规则QC-LDPC码的一种确定性构造方法[J]. 电子与信息学报, 2010, 32(5): 1152–1156. doi: 10.3724/SP.J.1146.2009.00838ZHANG Guohua, CHEN Chao, YANG Yang, et al. Girth-8 (3,L)-regular QC-LDPC codes based on novel deterministic design technique[J]. Journal of Electronics &Information Technology, 2010, 32(5): 1152–1156. doi: 10.3724/SP.J.1146.2009.00838 -






 下载:
下载:


 下载:
下载:
