合成多频磁感应信号同步激励-检测方法研究

杜强; 张可昊; 柯丽; 王晨阳

doi:10.11999/JEIT181083

合成多频磁感应信号同步激励-检测方法研究

doi: 10.11999/JEIT181083

沈阳工业大学电气工程学院沈阳 110870

基金项目: 国家自然科学基金(51377109)，辽宁省教育厅重点实验室基础研究项目(LZ2014011)

详细信息

作者简介:
杜强：男，1975年生，博士，讲师，研究方向为生物阻抗检测、人体电信号检测与分析

张可昊：男，1993年生，硕士生，研究方向为医学电磁工程及医疗仪器

柯丽：女，1977年生，博士，教授，博士生导师，研究方向为生物阻抗成像、医学电磁工程

王晨阳：男，1995年生，硕士生，研究方向为生物医学电子与信息技术

通讯作者:
柯丽　keli@sut.edu.cn

中图分类号: TM933
计量
- 文章访问数: 2138
- HTML全文浏览量: 952
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-26
- 修回日期: 2019-04-22
- 网络出版日期: 2019-04-29
- 刊出日期: 2019-09-10

Research on Synchronous Excitation and Detection Method for Synthetic Multi-frequency Magnetic Induction Signals

School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China

Funds: The National Natural Science Foundation of China (51377109), The Natural Science Foundation of Liaoning Province (LZ2014011)

摘要

摘要: 磁感应检测技术是一种非接触、无创的电阻抗检测技术，多频率同步检测可同时获得不同频率下被测对象的阻抗信息。该文首先研究了磁感应信号多频率同步激励与检测原理，基于Walsh函数合成了5频率激励信号。其次分析了合成多频率同步检测性能，设计了合成多频磁感应信号同步检测系统。最后，通过合成5频率激励信号与同步检测系统进行不同电导率NaCl溶液的检测实验，结果表明：合成5频率激励信号5个主谐波的测量结果都具有很好的线性度，为磁感应信号多频率同步检测提供了激励-检测方法。
- 磁感应信号 /
- 合成多频信号 /
- Walsh函数 /
- 电导率测量
Abstract: Magnetic induction detection technology is a non-contact and non-invasive electrical impedance detection technology. Multi-frequency synchronous detection can simultaneously obtain the impedance information of the tested object at different frequencies. Firstly, the principle of multi-frequency synchronous excitation and detection of magnetic induction signal are studied. Five-frequency excitation signal is synthesized based on Walsh function. Secondly, the performance of synthesized multi-frequency synchronous detection is analyzed, and a synthesized multi-frequency magnetic induction signal synchronous detection system is designed. Finally, the detection experiments of NaCl solution with different conductivities are carried out by synthesizing five-frequency excitation signal and synchronous detection system. The results show that the measurement results of five main harmonics of synthesized five-frequency excitation signal have good linearity. It provides an excitation-detection method for multi-frequency synchronous detection of magnetic induction signal.
- Magnetic induction signal /
- Synthetic multi-frequency signal /
- Walsh function /
- Conductivity measurement

HTML全文

图 1 合成多频磁感应信号同步激励-检测等效电路

下载: 全尺寸图片幻灯片

图 2 合成f (5, t)所需的5个Walsh函数

下载: 全尺寸图片幻灯片

图 3 合成的f (5, t)在单位周期[0, 1]上的波形

下载: 全尺寸图片幻灯片

图 4 f(5, t)的幅度谱和功率谱

下载: 全尺寸图片幻灯片

图 5 FPGA输出的f(5, t)信号

下载: 全尺寸图片幻灯片

图 6 FPGA输出的f(5, t)信号傅里叶变换结果

下载: 全尺寸图片幻灯片

图 7 同步激励-检测系统

下载: 全尺寸图片幻灯片

图 8 合成多频磁感应信号同步检测稳定性实验结果

下载: 全尺寸图片幻灯片

图 9 NaCl溶液的电导率和各谐波电压幅值差的关系图

下载: 全尺寸图片幻灯片

图 10 各主谐波平均幅值差$\Delta {b_k}$与电导率的关系

下载: 全尺寸图片幻灯片

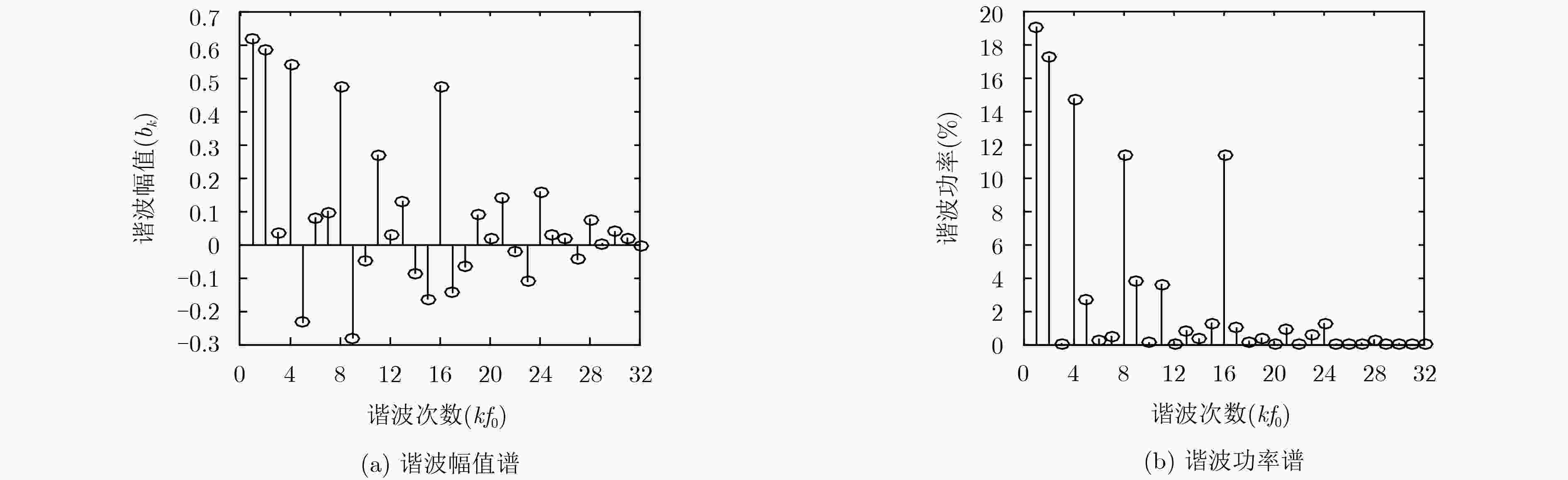
表 1 合成5频率同步信号f(5, t)的主谐波H_k频谱特性

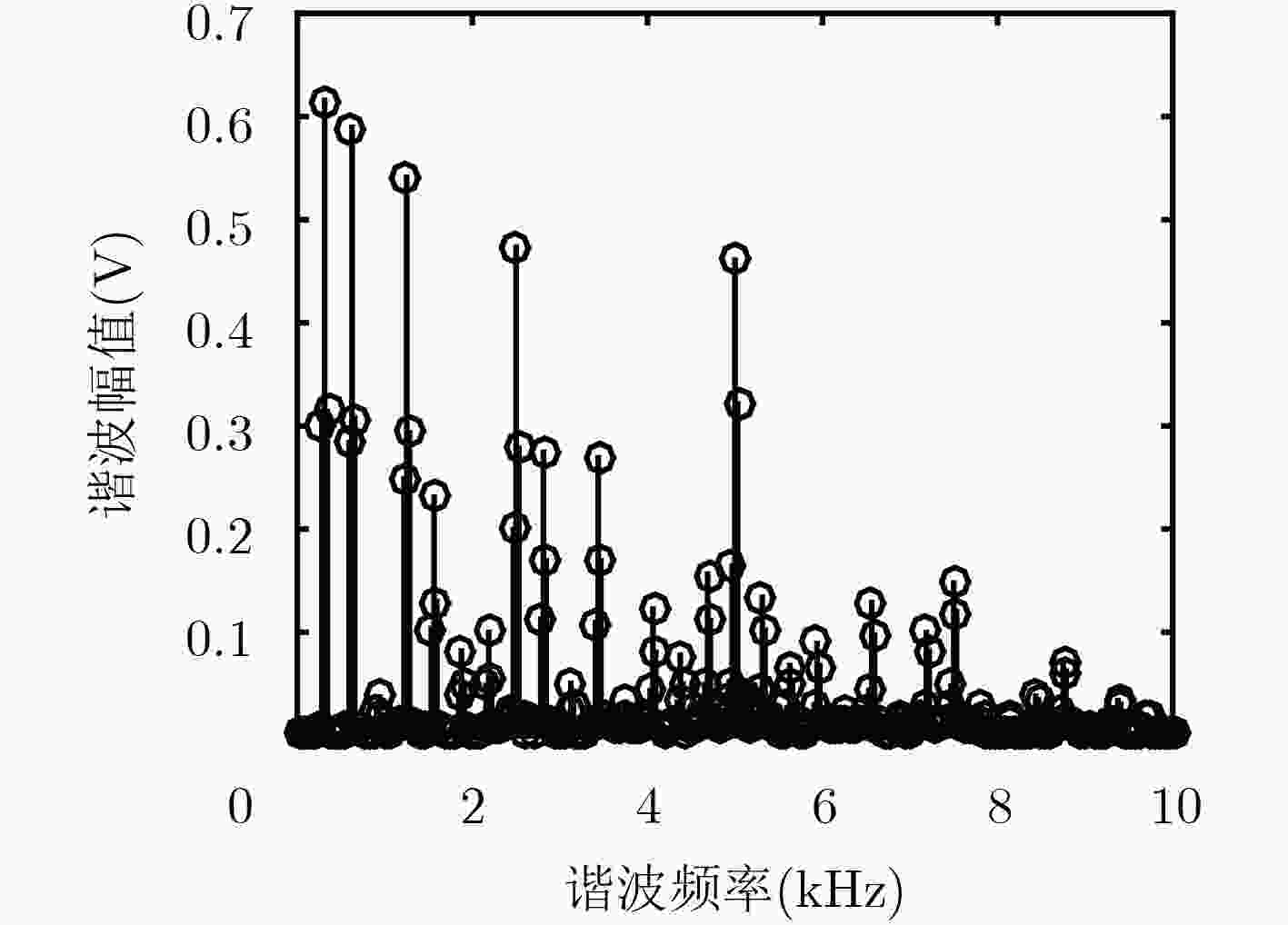
H_k	f₀	2f₀	4f₀	8f₀	16f₀	总和
b_k(V)	0.6173	0.5882	0.5443	0.4775	0.4775
P_k(%)	19.05	17.30	14.76	11.40	11.40	73.91

下载: 导出CSV

表 2 合成5频率激励信号f(5, t)的主谐波H_k频率值

H_k	f₀	2f₀	4f₀	8f₀	16f₀
T_clk=100 μs	312.5 Hz	625 Hz	1.25 kHz	2.5 kHz	5 kHz
T_clk=50 μs	625 Hz	1.25 kHz	2.5 kHz	5 kHz	10 kHz

下载: 导出CSV

表 3 电导率与NaCl溶液浓度关系表

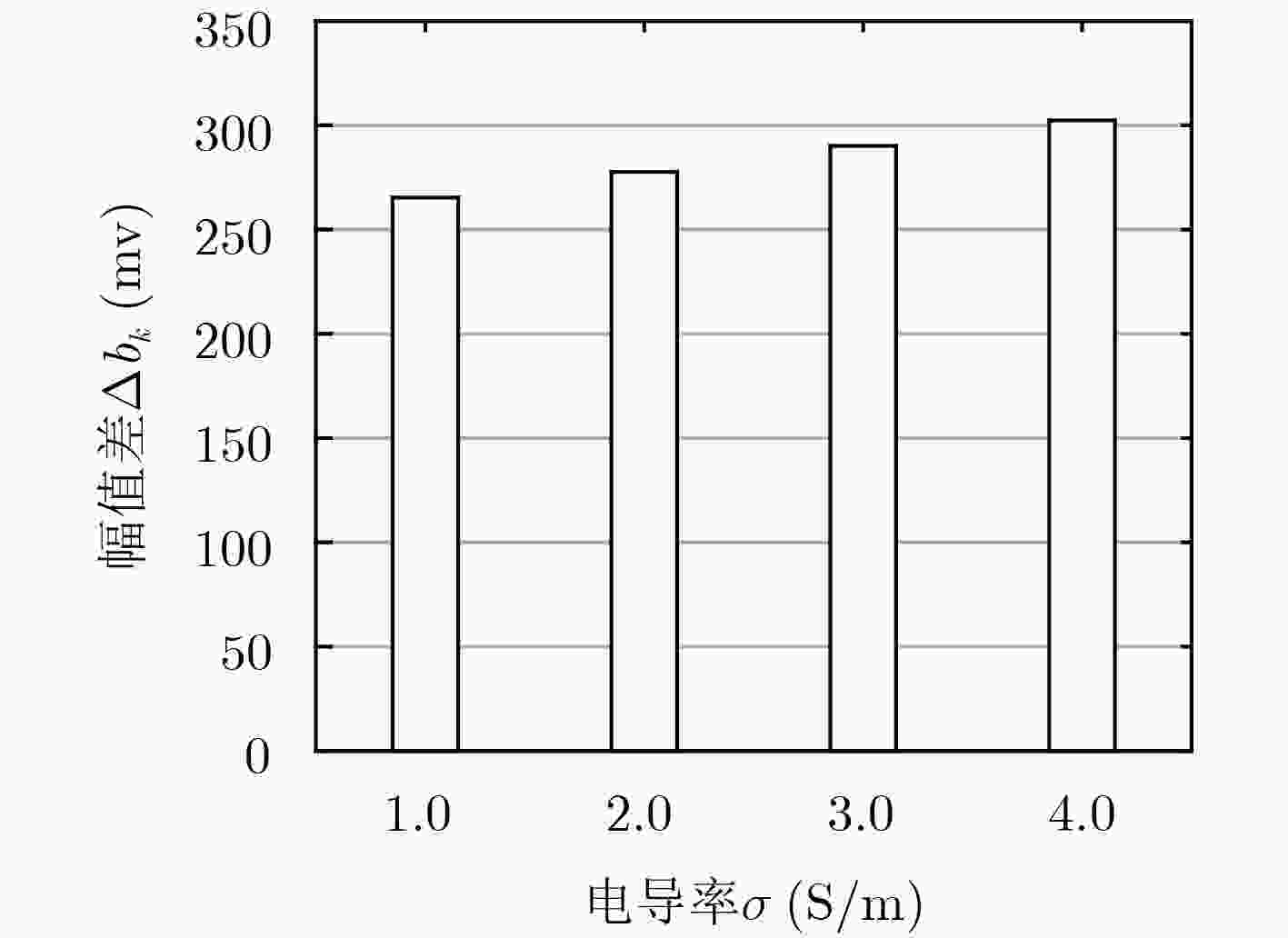
电导率$\sigma $(S/m)	1.0	2.0	3.0	4.0
ppm(mg/L)	5439	11476	17624	23713

下载: 导出CSV

表 4 不同电导率NaCl溶液同步检测结果

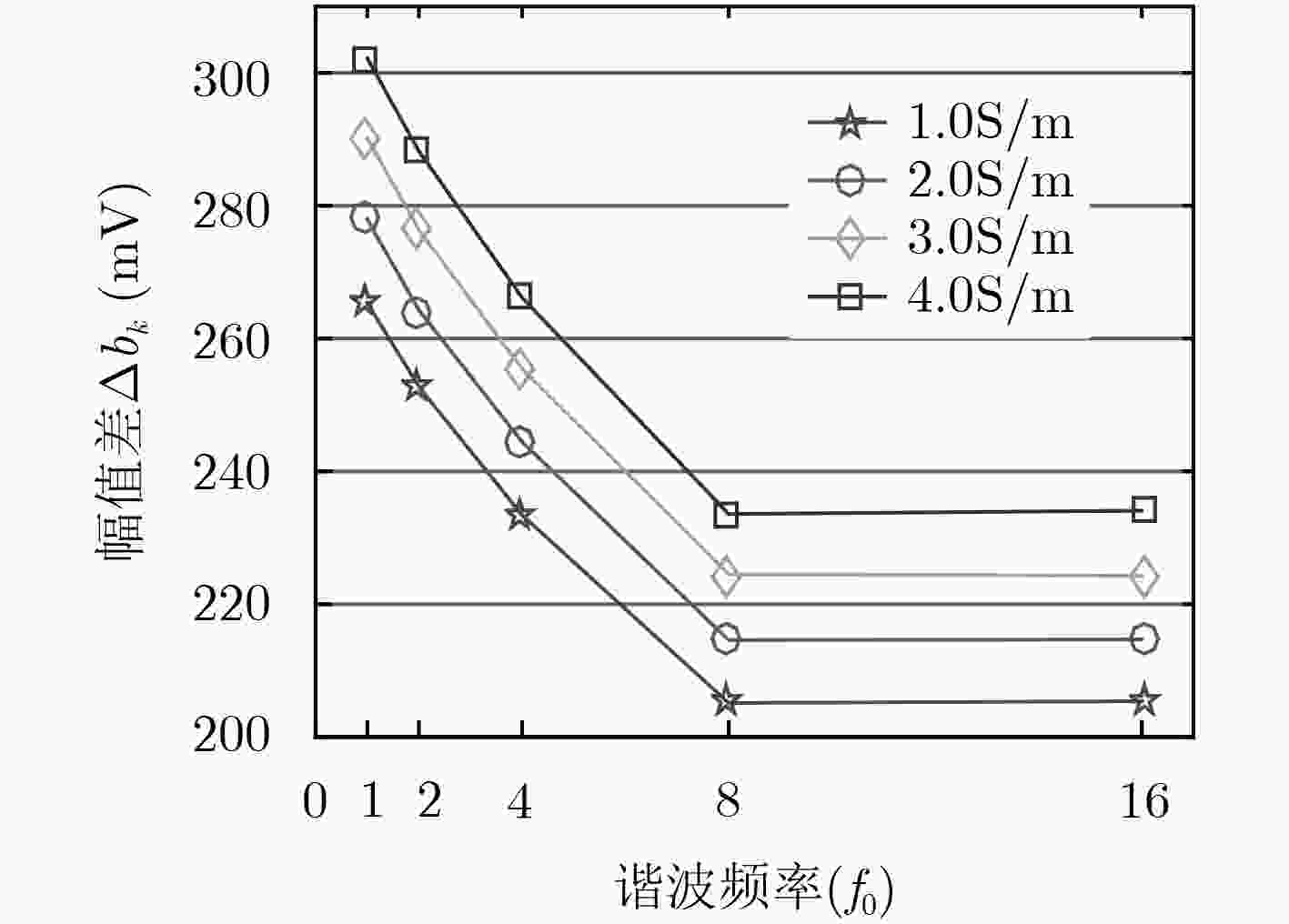
$\Delta {b_k}$(mV)	f₀	2f₀	4f₀	8f₀	16f₀
1.0 S/m	265.355	252.738	233.404	205.126	205.396
2.0 S/m	277.931	264.274	244.421	214.596	214.693
3.0 S/m	290.190	276.316	255.436	224.515	224.252
4.0 S/m	302.210	288.198	266.145	233.576	234.086

下载: 导出CSV

表 5 各谐波归一化系数

H_k	f₀	2f₀	4f₀	8f₀	16f₀
归一化系数	1.000	1.050	1.136	1.293	1.293

下载: 导出CSV

表 6 归一化处理后不同电导率NaCl溶液同步检测结果

$\Delta {b_k}$(mV)	f₀	2f₀	4f₀	8f₀	16f₀	平均值
1.0 S/m	265.355	265.269	265.160	265.210	265.560	265.311
2.0 S/m	277.931	277.377	277.677	277.454	277.579	277.603
3.0 S/m	290.190	290.016	290.190	290.279	289.939	290.123
4.0 S/m	302.210	302.487	302.356	301.993	302.653	302.340

下载: 导出CSV

参考文献(15)

GRIFFITHS H. Magnetic induction tomography[J]. Measurement Science and Technology, 2001, 12(8): 1126–1131. doi: 10.1088/0957-0233/12/8/319

YAN Qingguang, JIN Gui, QIN Mingxin, et al. Experimental study on the detection of rabbit intracranial hemorrhage using four coil structures based on magnetic induction phase shift[J]. Biomedizinische Technik Biomedical Engineering, 2017, 62(1): 1–14. doi: 10.1515/bmt-2015-0129

柯丽, 刘欢, 杜强, 等. 基于滤波反投影的脑磁感应迭代重建算法研究[J]. 仪器仪表学报, 2016, 31(11): 2445–2451. doi: 10.3969/j.issn.0254-3087.2016.11.005

KE Li, LIU Huan, DU Qiang, et al. Study on iterative reconstruction algorithm for brain magnetic induction based on filtered back-projection[J]. Chinese Journal of Scientific Instrument, 2016, 31(11): 2445–2451. doi: 10.3969/j.issn.0254-3087.2016.11.005

罗海军, 廖勇, 潘海涛, 等. 导数法峰值锐化算法提高磁感应成像图像分辨率[J]. 电子与信息学报, 2018, 40(8): 1847–1852. doi: 10.11999/JEIT171102

LUO Haijun, LIAO Yong, PAN Haitao, et al. Derivative method peak sharpening algorithm improves image resolution of magnetic induction tomography[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1847–1852. doi: 10.11999/JEIT171102

YIN Wuliang and PEYTON A J. Sensitivity formulation including velocity effects for electromagnetic induction systems[J]. IEEE Transactions on Magnetics, 2010, 46(5): 1172–1176. doi: 10.1109/TMAG.2009.2038275

MELLERT F, WINKLER K, SCHNEIDER C, et al. Detection of (reversible) myocardial ischemic injury by means of electrical bioimpedance[J]. IEEE Transactions on Biomedical Engineering, 2010, 58(6): 1511–1518. doi: 10.1109/TBME.2010.2054090

SUN T, HOLMES D, GAWAD S, et al. High speed multi-frequency impedance analysis of single particles in a microfluidic cytometer using maximum length sequences[J]. Lab on a Chip, 2007, 7(8): 1034–1040. doi: 10.1039/b703546b

鞠康, 何为, 何传红, 等. 基于直接数字频率合成的混合频率恒流源设计[J]. 仪器仪表学报, 2010, 31(9): 2109–2114. doi: 10.19650/j.cnki.cjsi.2010.09.030

JU Kang, HE Wei, HE Chuanhong, et al. Design of mixing frequency constant current source based on direct digital synthesizer[J]. Chinese Journal of Scientific Instrument, 2010, 31(9): 2109–2114. doi: 10.19650/j.cnki.cjsi.2010.09.030

BRUNNER P, MERWA R, MISSNER A, et al. Reconstruction of the shape of conductivity spectra using differential multi-frequency magnetic induction tomography[J]. Physiological Measurement, 2006, 27: 237–248. doi: 10.1088/0967-3334/27/5/S20

GURSOY D and SCHARFETTER H. Feasibility of head imaging using multi-frequency magnetic induction tomography[C]. Biomedical Engineering Meeting, Heidelberg, Germany, 2009, 525–528.

XIAO Zhili, TAN Chao, and DONG Feng. Effect of inter-tissue inductive coupling on multi-frequency imaging of intracranial hemorrhage by magnetic induction tomography[J]. Measurement Science and Technology, 2017, 28(8): 1–11. doi: 10.1088/1361-6501/aa7504

MA Lu and SOLEIMANI M. Magnetic induction tomography methods and applications: A review[J]. Measurement Science and Technology, 2017, 28(7): 072001. doi: 10.1088/1361-6501/aa7107

吕轶, 王旭, 杨丹, 等. 一种磁感应成像中生物组织涡流信号的新型测量方法[J]. 电子与信息学报, 2011, 33(9): 2258–2262. doi: 10.3724/SP.J.1146.2010.01422

LÜ Yi, WANG Xu, YANG Dan, et al. A new measurement method of eddy current for biological tissue in magnetic induction tomography[J]. Journal of Electronics &Information Technology, 2011, 33(9): 2258–2262. doi: 10.3724/SP.J.1146.2010.01422

王超, 郎健, 王化祥. 用于生物阻抗测量的混频激励电流源[J]. 计量学报, 2006, 27(4): 392–396. doi: 10.3321/j.issn:1000-1158.2006.04.023

WANG Chao, LANG Jian, and WANG Huaxiang. Mixing frequency excitation current source used in bioelectric impedance measuring system[J]. Acta Metrologica Sinica, 2006, 27(4): 392–396. doi: 10.3321/j.issn:1000-1158.2006.04.023

杨宇祥, 乔洋. 一种多频率同步信号激励电流源设计[J]. 仪器仪表学报, 2013, 34(4): 908–913. doi: 10.19650/j.cnki.cjsi.2013.04.029

YANG Yuxiang and QIAO Yang. Design of a multi-frequency synchronized signal excitation current source[J]. Chinese Journal of Scientific Instrument, 2013, 34(4): 908–913. doi: 10.19650/j.cnki.cjsi.2013.04.029

施引文献

资源附件(0)

访问统计