Performance Analysis of Short Reference Orthogonal Multiuser Differential Chaotic Shift Keying Scheme
-
摘要: 针对差分混沌移位键控(DCSK)传输率低这一缺点，以及为了进一步改善系统的误码性能，该文提出一种短参考正交多用户DCSK(SOM-DCSK)通信系统。该系统将参考信号缩短为每个信息承载信号的1/P，通过延迟时间的不同传输多个用户，然后在每个信息时隙中利用希尔伯特变换的正交性达到传输2 bit信息信号的目的。该文推导了SOM-DCSK系统在加性高斯白噪声(AWGN)和Rayleigh衰落信道下的比特误码率(BER)公式并进行了实验仿真。仿真结果表明：相同条件下，该方案相比于传统多用户系统的误码性能有了明显的改进，具有很好的实用价值。Abstract: Considering the shortcomings of Differential Chaos Shift Keying (DCSK) transmission rate and to further improve the system error performance, a Short reference Orthogonal Multiuser DCSK(SOM-DCSK) communication system is proposed. The system shortens the reference signal to 1/P of each information bearing signal, and transmits multiple users by different delay times. Then the orthogonality of Hilbert transform is used in each information slot to achieve the purpose of transmitting a two-bit information signal. The Bite Error Rate (BER) formula of SOM-DCSK system in Additive White Gaussian Noise (AWGN) and Rayleigh fading channel is derived and experimentally simulated. The simulation results show that BER of the scheme has obvious improvement compared with the traditional multi-user system under the same conditions, and it has good practical value.
-
陈志刚, 梁涤青, 邓小鸿, 等. Logistic混沌映射性能分析与改进[J]. 电子与信息学报, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039CHEN Zhigang, LIANG Diqing, DENG Xiaohong, et al. Performance analysis and improvement of logistic chaotic mapping[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039 TONG Xiaojun. Design of an image encryption scheme based on a multiple chaotic map[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1725–1733. doi: 10.1016/j.cnsns.2012.11.002 LEE T F. Enhancing the security of password authenticated key agreement protocols based on chaotic maps[J]. Information Sciences, 2015, 290: 63–71. doi: 10.1016/j.ins.2014.08.041 KADDOUM G, TRAN H V, KONG L, et al. Design of simultaneous wireless information and power transfer scheme for short reference DCSK communication systems[J]. IEEE Transactions on Communications, 2017, 65(1): 431–443. doi: 10.1109/TCOMM.2016.2619707 KENNEDY M P, KOLUMBÁN G, and KIS G. Chaotic modulation for robust digital communications over multipath channels[J]. International Journal of Bifurcation and Chaos, 2000, 10(4): 695–718. doi: 10.1142/S0218127400000499 LÜ Yibo, WANG Ling, CAI Guofa, et al. Iterative receiver for M-ary DCSK systems[J]. IEEE Transactions on Communications, 2015, 63(11): 3929–3936. doi: 10.1109/TCOMM.2015.2425877 HASLER M and SCHIMMING T. Chaos communication over noisy channels[J]. International Journal of Bifurcation and Chaos, 2000, 10(4): 719–735. doi: 10.1142/S0218127400000505 KADDOUM G and SOUJERI E. NR-DCSK: A noise reduction differential chaos shift keying system[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2016, 63(7): 648–652. doi: 10.1109/TCSII.2016.2532041 DAWA M, KADDOUM G, and SATTAR Z. A generalized lower bound on the bit error rate of DCSK systems over multi-path Rayleigh fading channels[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(3): 321–325. doi: 10.1109/TCSII.2017.2733381 KOLUMBAN G, VIZVÁRI B, SCHWARZ W, et al. Differential chaos shift keying: A robust coding for chaotic communication[C]. The 4th International Specialist Workshop on Nonlinear Dynamics of Electronic Systems, Seville, Spain, 1996: 87–92. SUSHCHIK M, TSIMRING L S, and VOLKOVSKII A R. Performance analysis of correlation-based communication schemes utilizing chaos[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(12): 1684–1691. doi: 10.1109/81.899920 KADDOUM G, SOUJERI E, and NIJSURE Y. Design of a short reference noncoherent chaos-based communication systems[J]. IEEE Transactions on Communications, 2016, 64(2): 680–689. doi: 10.1109/TCOMM.2015.2514089 GALIAS Z and MAGGIO G M. Quadrature chaos-shift keying: Theory and performance analysis[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001, 48(12): 1510–1519. doi: 10.1109/TCSI.2001.972858 LAU F C M, YIP M M, TSE C K, et al. A multiple-access technique for differential chaos-shift keying[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(1): 96–104. 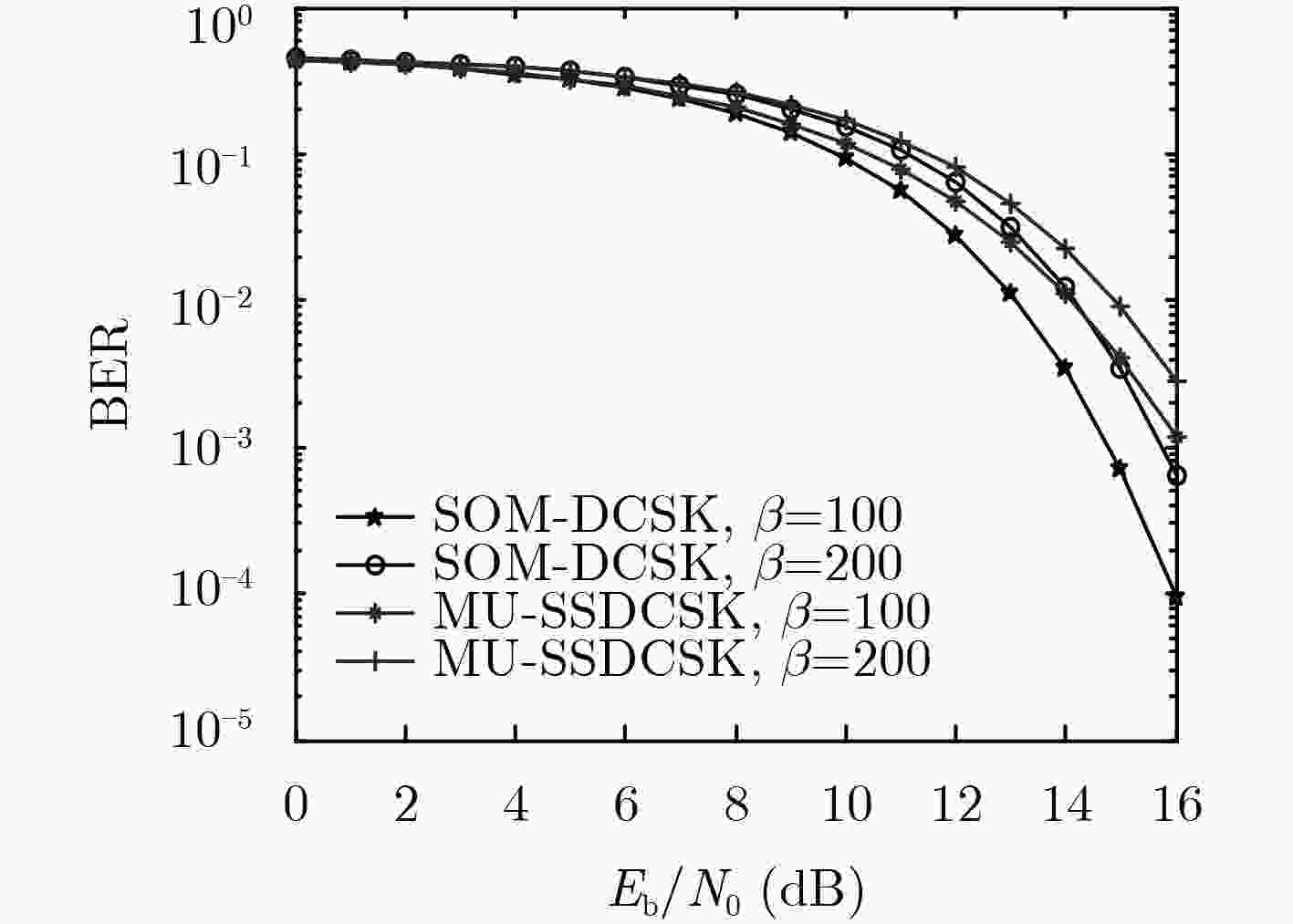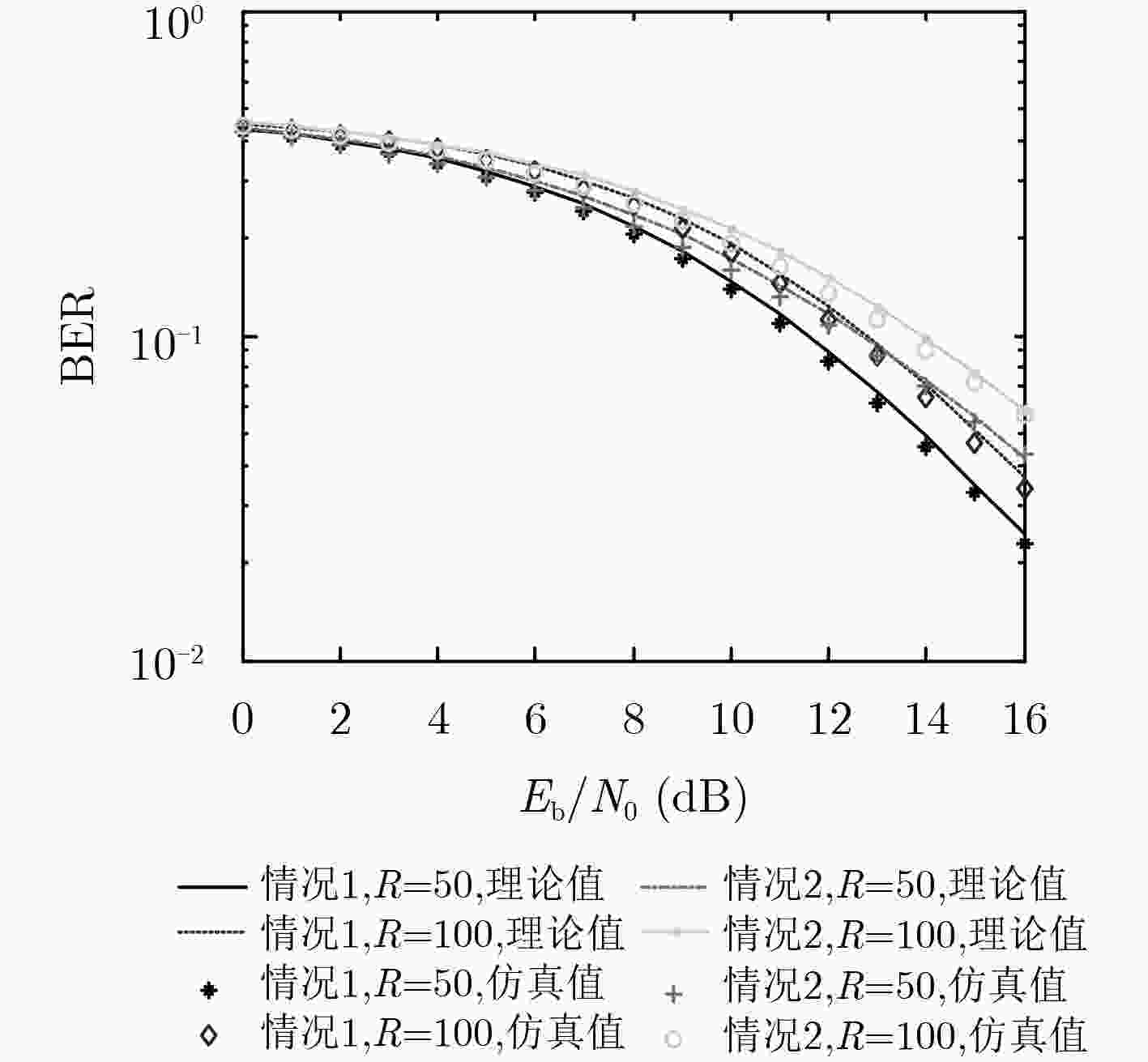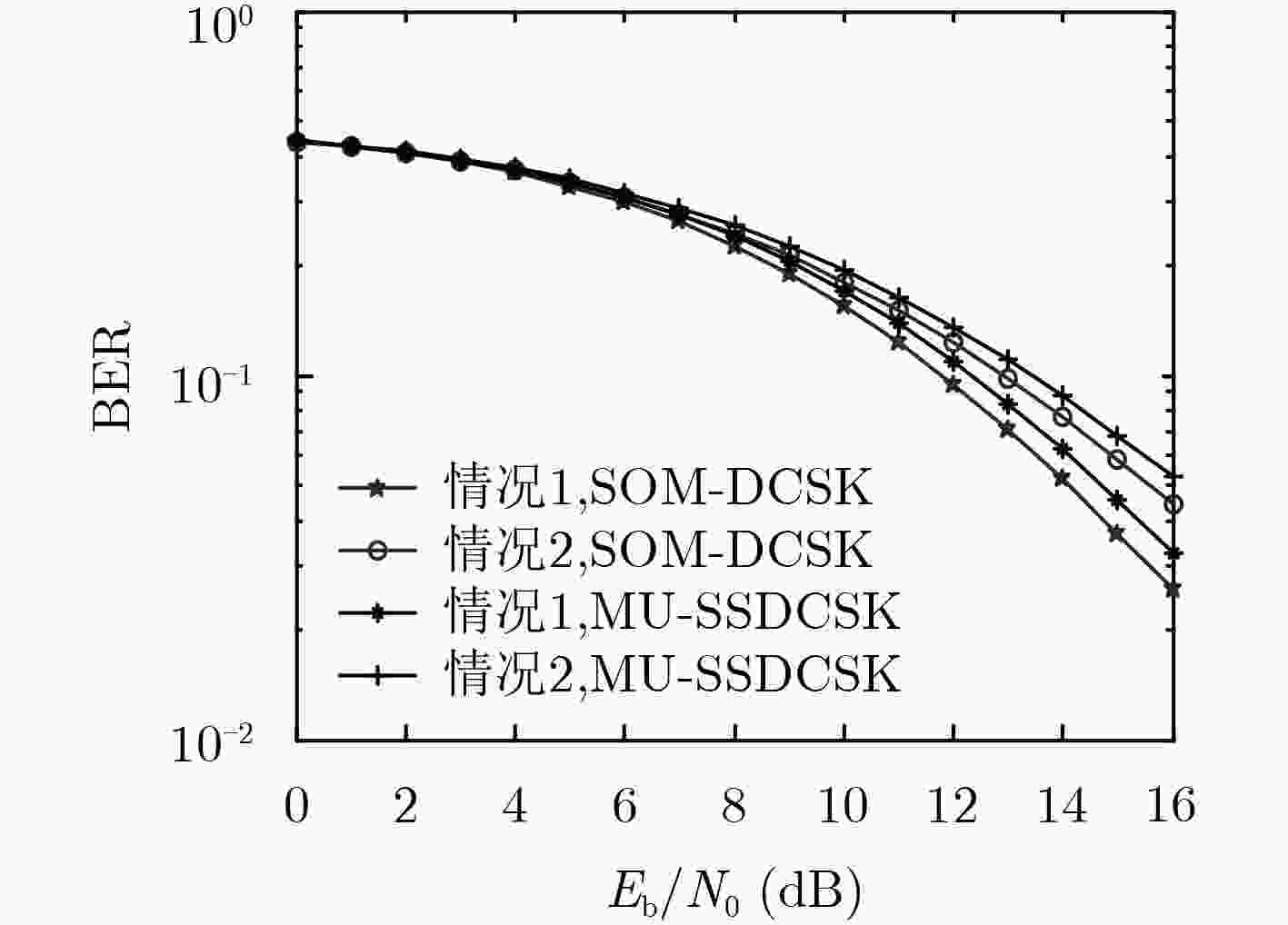doi: 10.1109/81.974883 YANG Hua, TANG W K S, CHEN Guanrong, et al. System design and performance analysis of orthogonal multi-level differential chaos shift keying modulation scheme[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(1): 146–156. 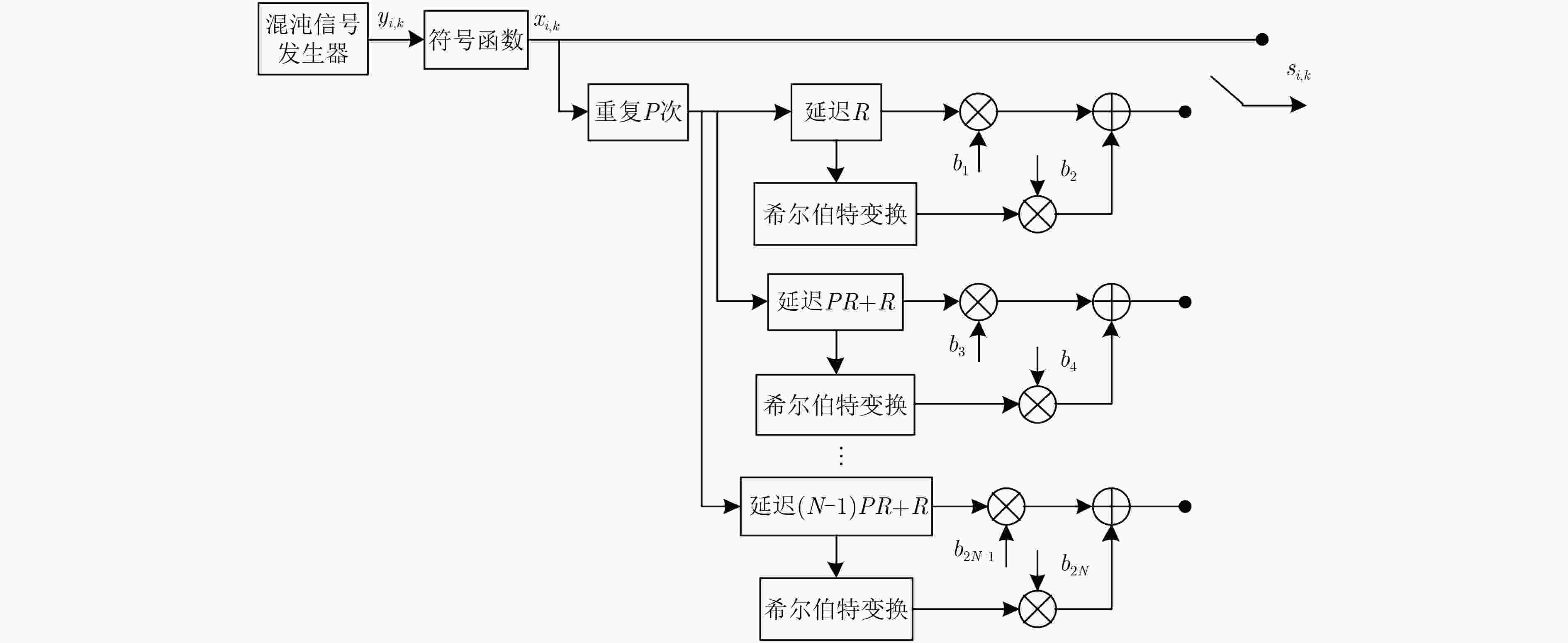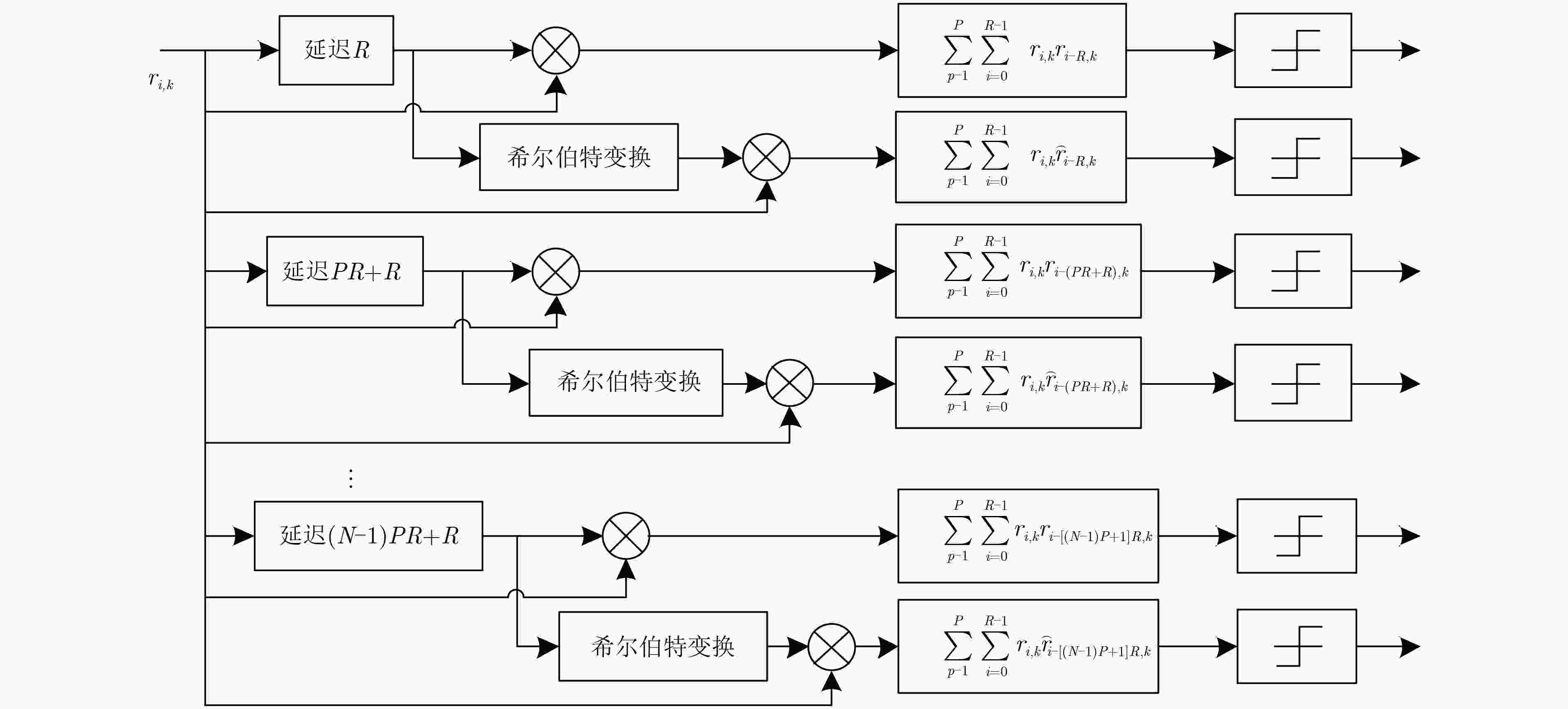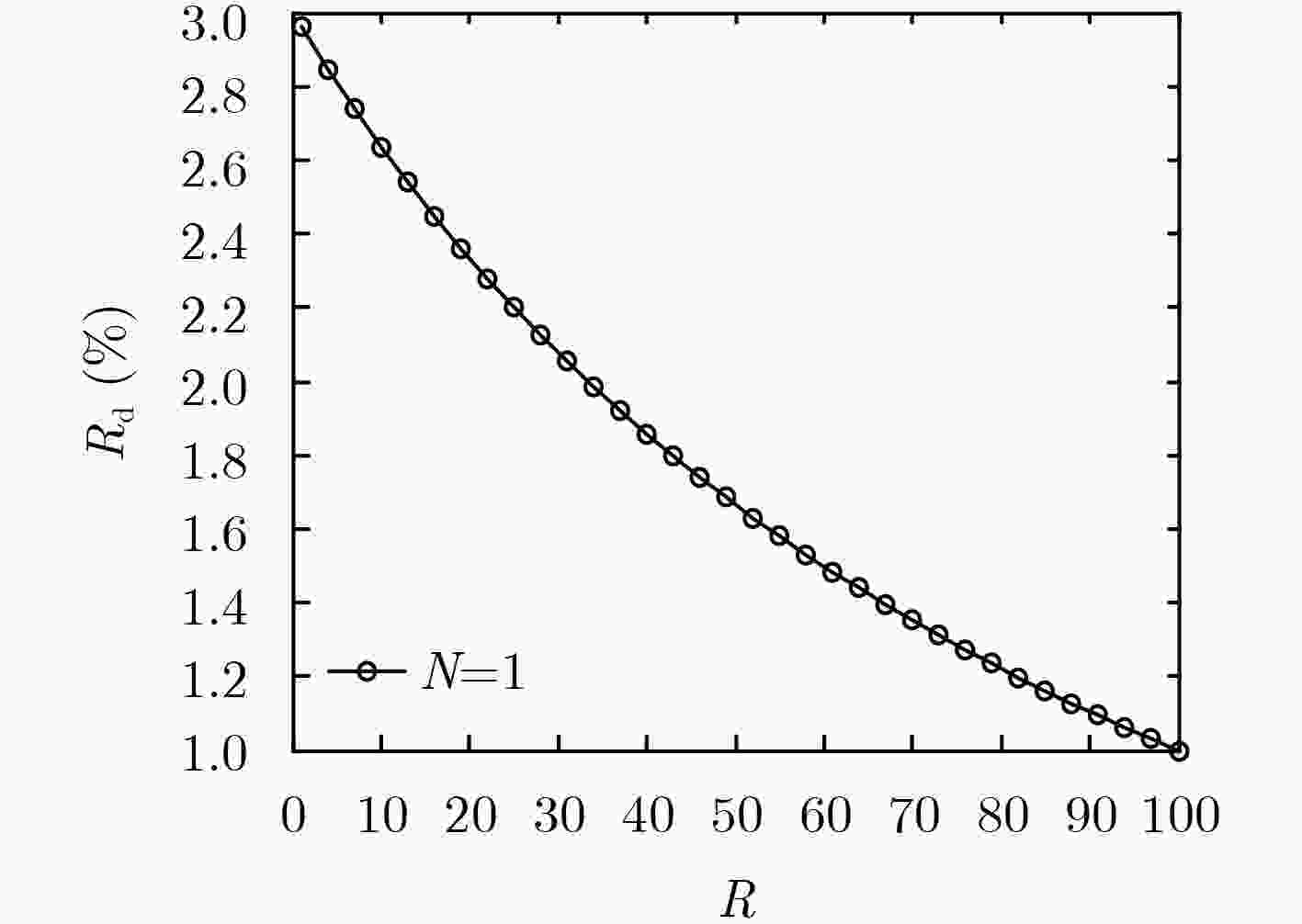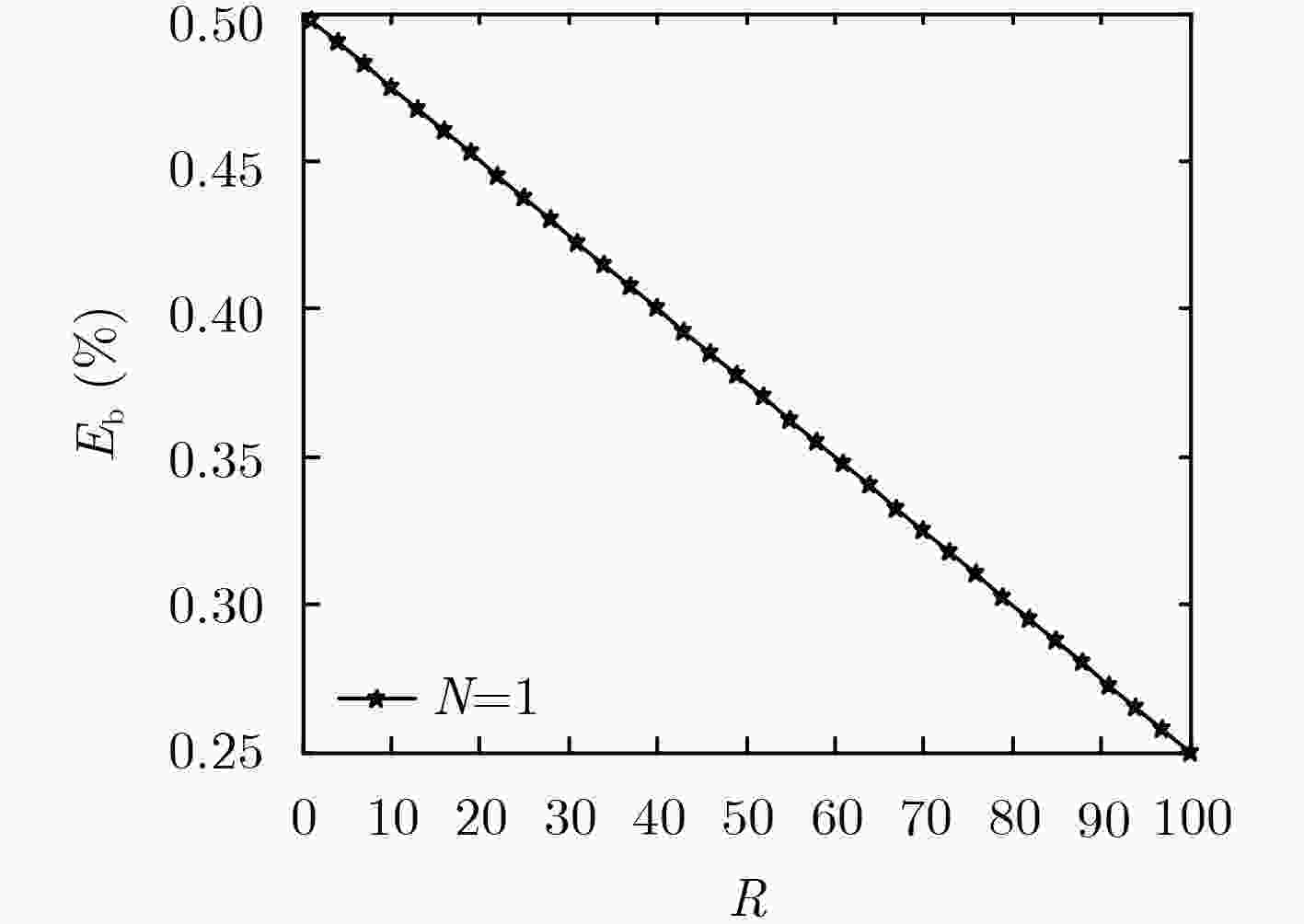doi: 10.1109/TCSI.2015.2510622 张刚, 孟维, 张天骐. 多用户分段移位差分混沌键控通信方案[J]. 电子与信息学报, 2017, 39(5): 1219–1225. doi: 10.11999/JEIT160795ZHANG Gang, MENG Wei, and ZHANG Tianqi. Multiuser communication scheme based on segment shift differential chaos shift keying[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1219–1225. doi: 10.11999/JEIT160795 MANDAL S and BANERJEE S. Analysis and CMOS implementation of a chaos-based communication system[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(9): 1708–1722. doi: 10.1109/TCSI.2004.834482 -
下载:
图(12)
计量
- 文章访问数: 2060
- HTML全文浏览量: 714
- PDF下载量: 54
- 被引次数: 0
下载:
