Repair and Restoration of Corrupted Compressed Files
-
摘要: 数据压缩和解压缩已广泛应用于现代通信和数据传输领域。但是如何解压缩损坏的无损压缩文件仍然是一个挑战。针对在通用编码领域广泛使用的无损数据压缩算法，该文提出一种能够修复误码并解压还原损坏的LZSS文件的有效方法，并给出了理论依据。该方法通过利用编码器留下的残留冗余携带校验信息，在不损失任何压缩性能的情况下，能够修复LZSS压缩数据中的错误。所提方法不需要增加额外比特，也不改变编码规则和数据格式，所以与标准算法完全兼容。即采用具有错误修复能力的LZSS方案压缩的数据，仍然可以通过标准LZSS解码器进行解压。实验结果验证了所提算法的有效性和实用性。Abstract: Data compression and decompression are widely used in modern communication and data transmission. However, how to decompress the damaged lossless compressed files is still a challenge. For the lossless data compression algorithm widely used in the general coding field, an effective method is proposed to repair the error and decompress and restore the corrupted LZSS files, and the theoretical basis is given. By using the residual redundancy left by the encoder to carry the check information, the method can repair the errors in LZSS compressed data without loss of any compression performance. The proposed method does not require additional bits or changes in coding rules and data formats, thus it is fully compatible with standard algorithms. That is, the data compressed by LZSS with error repair capability can still be decompressed by standard LZSS decoder. The experimental results verify the validity and practicability of the proposed algorithm.
-
Key words:
- Compressed files /
- Residual redundancy /
- Multiple matching /
- Error repair
-
DRMOTA M and SZPANKOWSKI W. Redundancy of lossless data compression for known sources by analytic methods[J]. Foundations and Trends in Communications and Information Theory, 2016, 13(4): 277–417. doi: 10.1561/0100000090 DAS S, BULL D M, and WHATMOUGH P N. Error-resilient design techniques for reliable and dependable computing[J]. IEEE Transactions on Device and Materials Reliability, 2015, 15(1): 24–34. doi: 10.1109/TDMR.2015.2389038 MENGHWAR G D and MECKLENBRAUKER C F. Cooperative versus non-cooperative communications[C]. The 2nd International Conference on Computer, Control and Communication, Karachi, Pakistan, 2009: 1–3. HAMSCHIN B M, FERGUSON J D, and GRABBE M T. Interception of multiple low-power linear frequency modulated continuous wave signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 789–804. 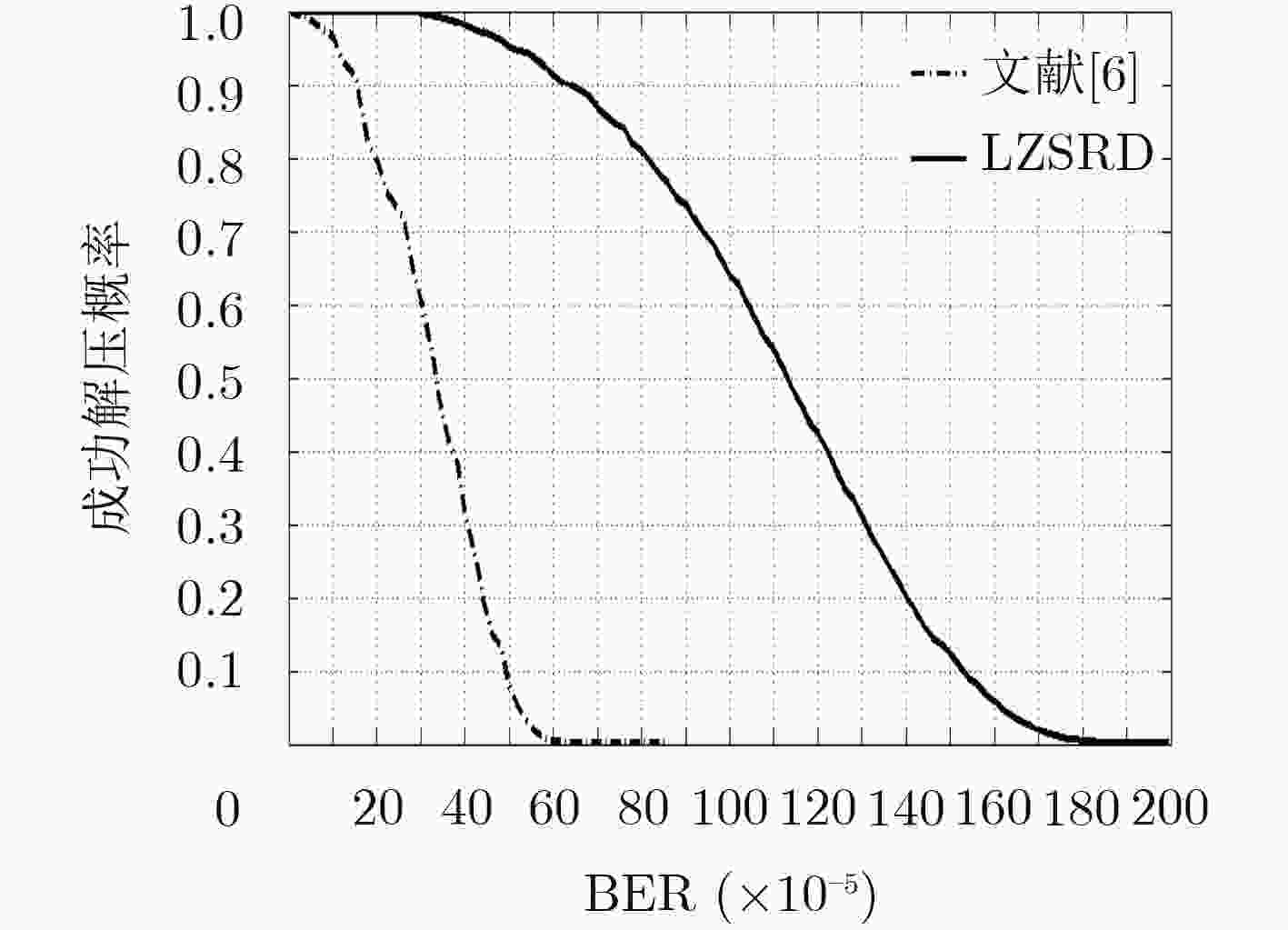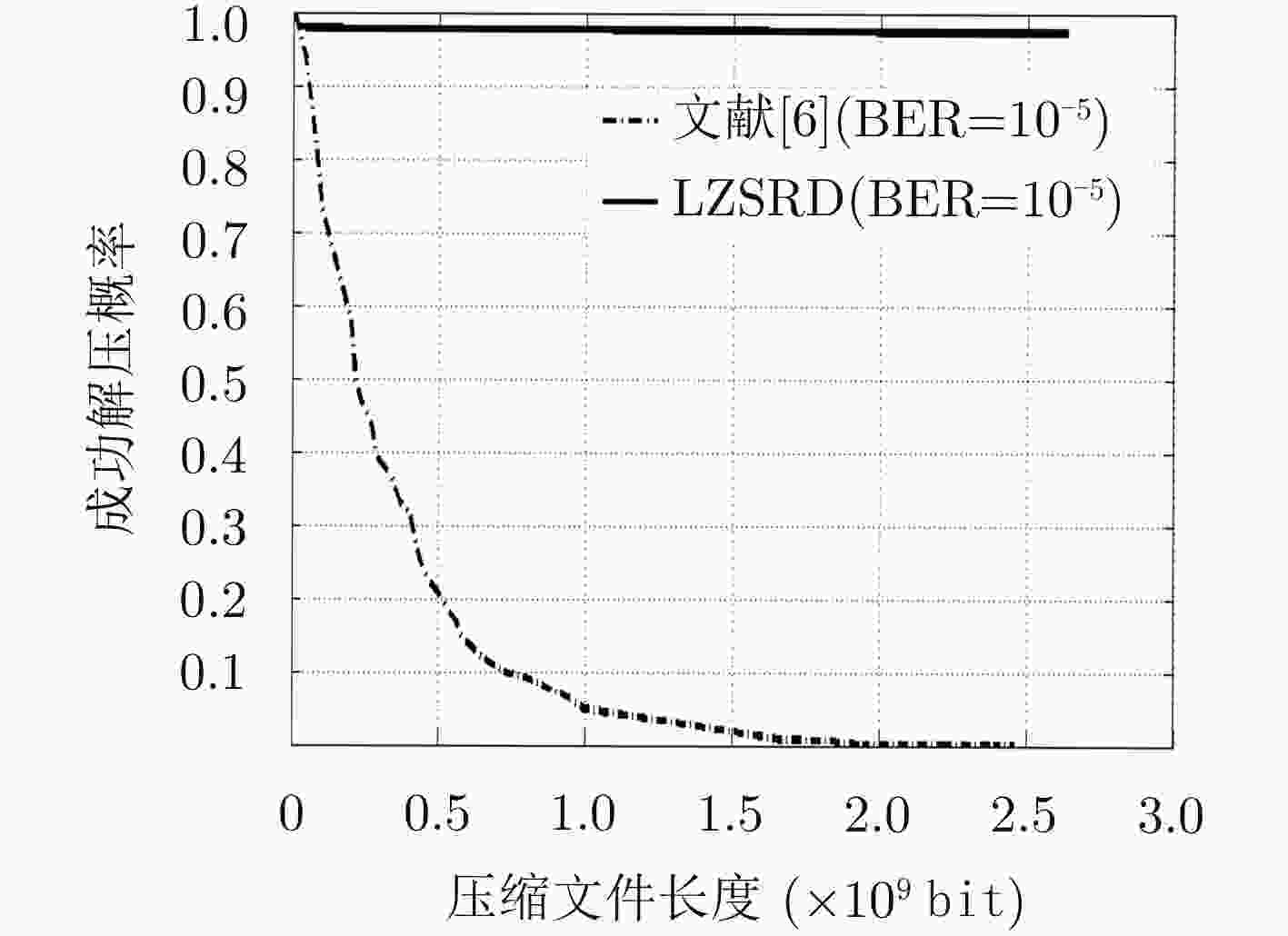doi: 10.1109/TAES.2017.2665140 KWON B, GONG M, and LEE S. Novel error detection algorithm for LZSS compressed data[J]. IEEE Access, 2017, 5: 8940–8947. doi: 10.1109/ACCESS.2017.2704900 WANG Digang, ZHAO Xiaoqun, and SUN Qingquan. Novel fault-tolerant decompression method of corrupted Huffman files[J]. Wireless Personal Communications, 2018, 102(4): 2555–2574. doi: 10.1007/s11277-018-5277-5 KOSTINA V, POLYANSKIY Y, and VERDú S. Variable-length compression allowing errors[J]. IEEE Transactions on Information Theory, 2015, 61(8): 4316–4330. doi: 10.1109/TIT.2015.2438831 ZHANG Jie, YANG Enhui, and KIEFFER J C. A universal grammar-based code for lossless compression of binary trees[J]. IEEE Transactions on Information Theory, 2014, 60(3): 1373–1386. doi: 10.1109/TIT.2013.2295392 KLEIN S T and SHAPIRA D. Practical fixed length Lempel-Ziv coding[J]. Discrete Applied Mathematics, 2014, 163: 326–333. doi: 10.1016/j.dam.2013.08.022 KITAKAMI M and KAWASAKI T. Burst error recovery method for LZSS coding[J]. IEICE Transactions on Information and Systems, 2009, E92.D(12): 2439–2444. doi: 10.1587/transinf.e92.d.2439 PEREIRA Z C, PELLENZ M E, SOUZA R D, et al. Unequal error protection for LZSS compressed data using Reed-Solomon codes[J]. IET Communications, 2007, 1(4): 612–617. doi: 10.1049/iet-com:20060530 LAKHANI G. Reducing coding redundancy in LZW[J]. Information Sciences, 2006, 176(10): 1417–1434. doi: 10.1016/j.ins.2005.03.007 PARK B, SAVOLDI A, GUBIAN P, et al. Recovery of damaged compressed files for digital forensic purposes[C]. 2008 International Conference on Multimedia and Ubiquitous Engineering, Busan, South Korea, 2008: 365–372. doi: 10.1109/MUE.2008.49. KOSTINA V, POLYANSKIY Y, and VERD S. Joint source-channel coding with feedback[J]. IEEE Transactions on Information Theory, 2017, 63(6): 3502–3515. doi: 10.1109/TIT.2017.2674667 KEMPA D and KOSOLOBOV D. LZ-end parsing in compressed space[C]. 2017 Data Compression Conference, Snowbird, USA, 2017: 350–359. 徐金甫, 刘露, 李伟, 等. 一种基于阵列配置加速比模型的无损压缩算法[J]. 电子与信息学报, 2018, 40(6): 1492–1498. doi: 10.11999/JEIT170900XU Jinfu, LIU Lu, LI Wei, et al. A new lossless compression algorithm based on array configuration speedup model[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1492–1498. doi: 10.11999/JEIT170900 DO H H, JANSSON J, SADAKANE K, et al. Fast relative Lempel-Ziv self-index for similar sequences[J]. Theoretical Computer Science, 2014, 532: 14–30. doi: 10.1016/j.tcs.2013.07.024 ATALLAH M J and LONARDI S. Augmenting LZ-77 with authentication and integrity assurance capabilities[J]. Concurrency and Computation: Practice and Experience, 2004, 16(11): 1063–1076. doi: 10.1002/cpe.804 REED I S and SOLOMON G. Polynomial codes over certain finite fields[J]. Journal of the Society for Industrial and Applied Mathematics, 1960, 8(2): 300–304. doi: 10.1137/0108018 WARD M D and SZPANKOWSKI W. Analysis of a randomized selection algorithm motivated by the LZ'77 scheme[C]. The 1st Workshop on Analytic Algorithmics and Combinatorics, New Orleans, USA, 2004: 153–160. JACQUET P and SZPANKOWSKI W. Analytical depoissonization and its applications[J]. Theoretical Computer Science, 1998, 201(1/2): 1–62. 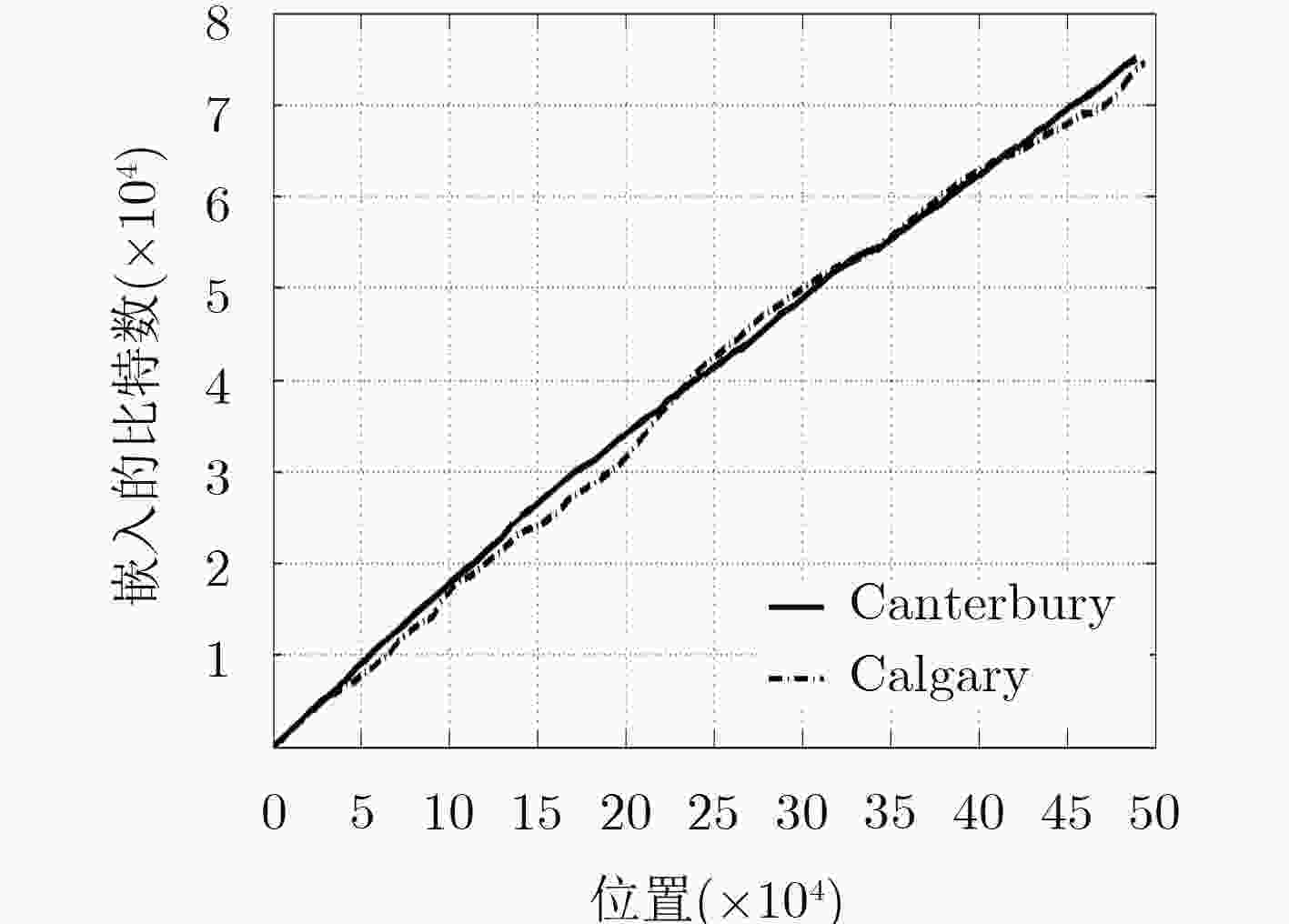doi: 10.1016/S0304-3975(97)00167-9 The Canterbury corpus[EB/OL]. http://corpus.canterbury.ac.nz/descriptions/#cantrbry, 2018. The Calgary corpus[EB/OL]. http://corpus.canterbury.ac.nz/descriptions/#calgary, 2018. -
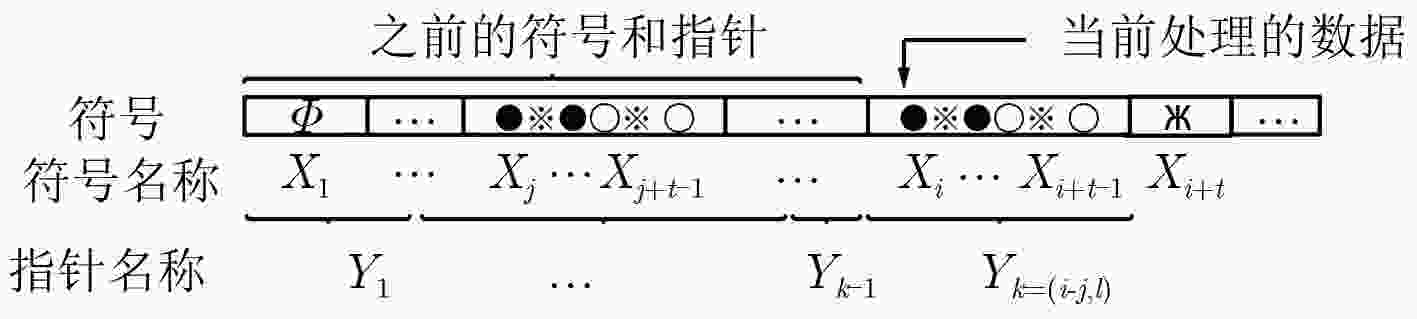
下载:
图(8)
计量
- 文章访问数: 3111
- HTML全文浏览量: 1204
- PDF下载量: 62
- 被引次数: 0
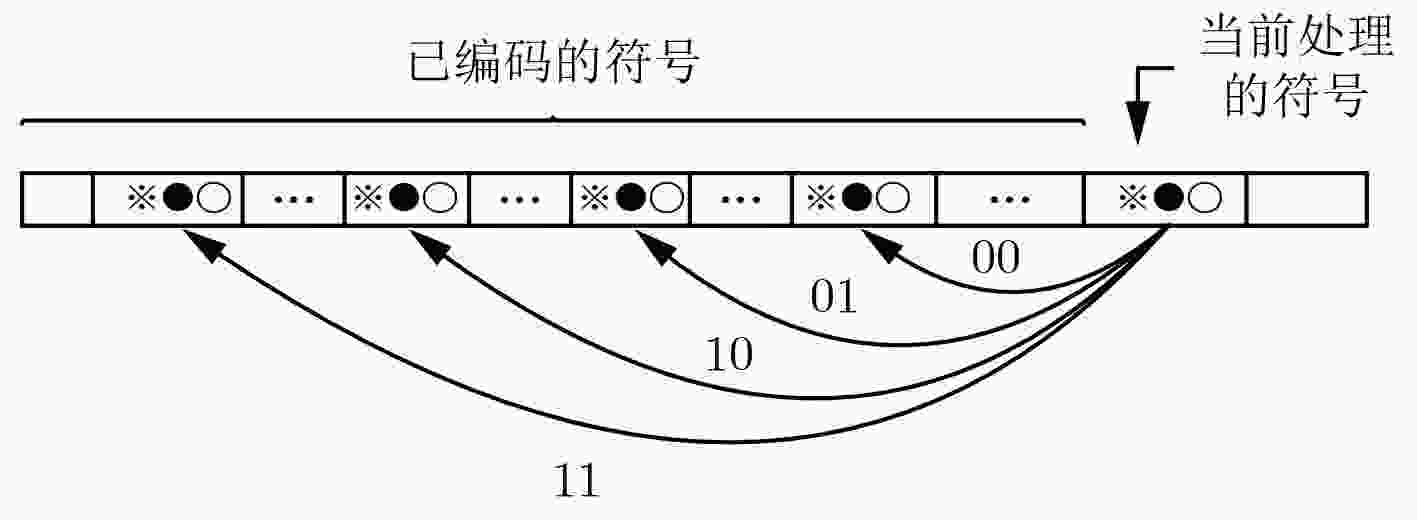
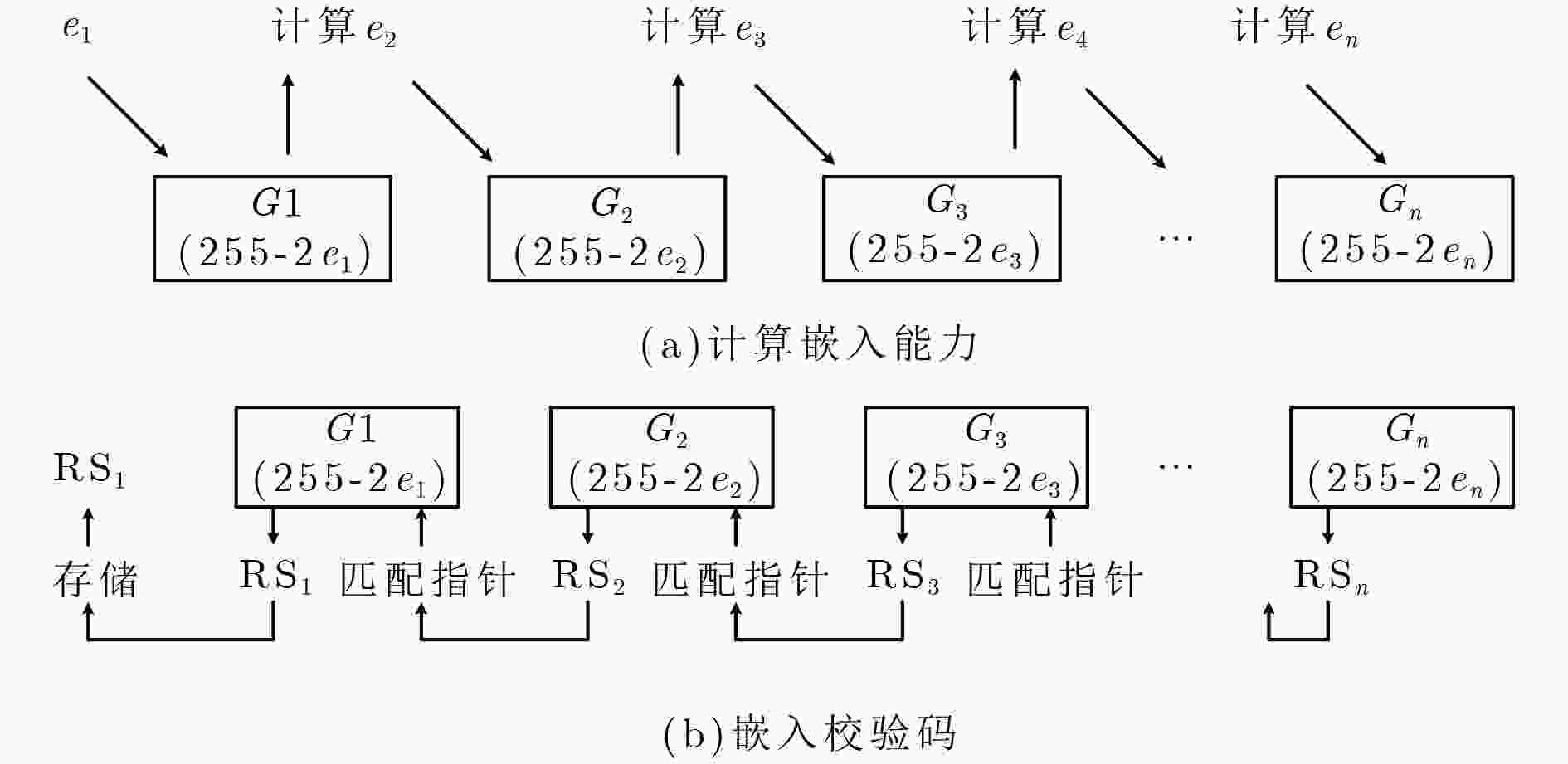
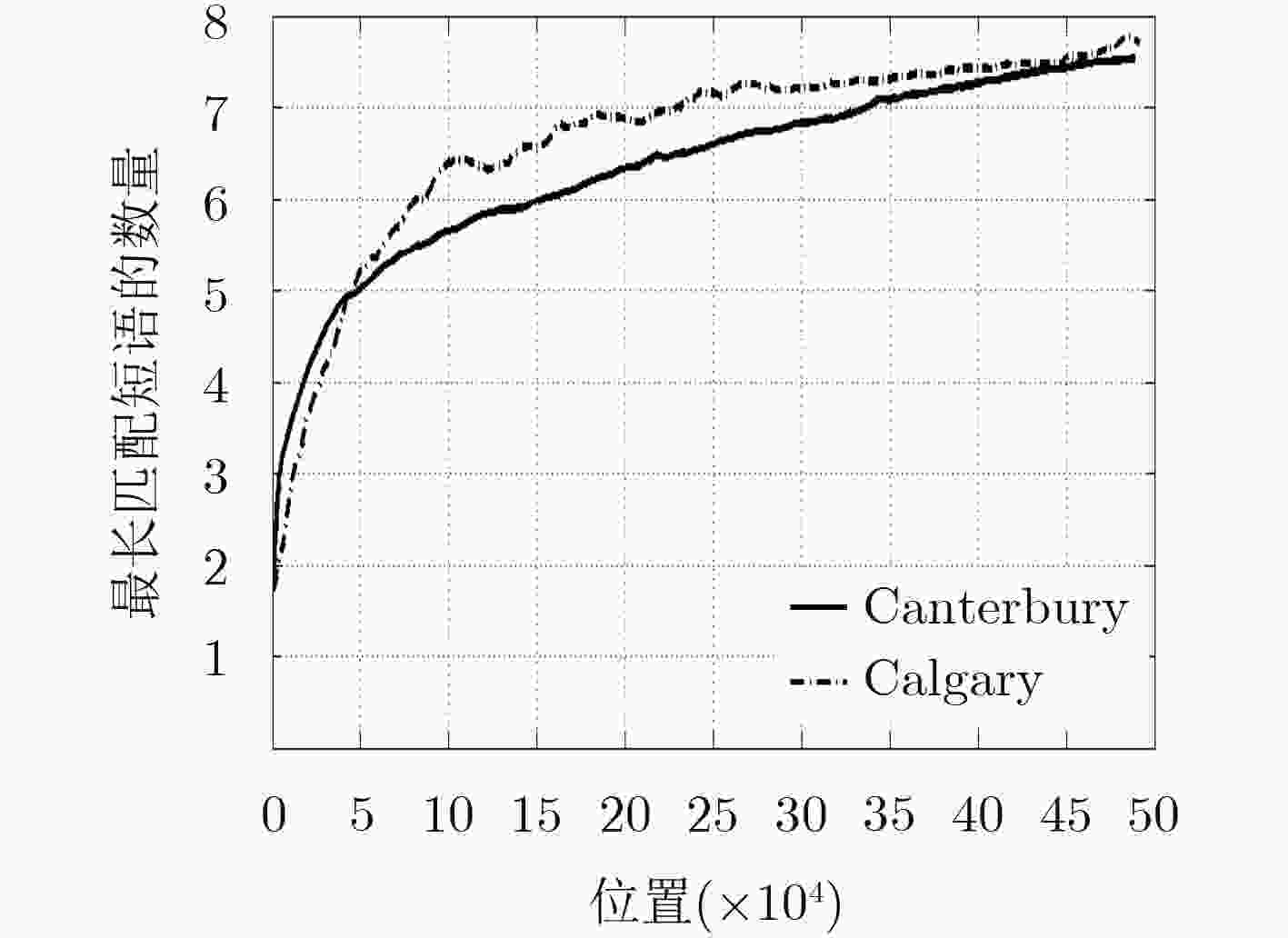
下载:
