Multi-priority Based Joint Optimization Algorithm of Virtual Network Function Migration Cost and Network Energy Consumption
-
摘要: 针对5G接入网络中虚拟网络功能(VNF)部署完成后,其资源需求发生动态变化,导致网络中物理机(PM)资源利用率过高或过低这一问题,该文首先将网络中PM的资源使用情况划分5个不同分区,提出一种多优先级VNF迁移请求队列调度模型。其次基于该模型,对VNF迁移开销的最小化及网络能耗的最小化建立联合优化模型。最后提出一种基于5G接入网络的多优先级VNF迁移开销与网络能耗联合优化算法对其进行求解。仿真结果表明,该算法在有效实现VNF迁移开销与网络能耗折中的同时,提高了PM资源利用率,保证了PM性能并均衡各PM负载。Abstract: After the Virtual Network Function (VNF) in the 5G access network is deployed, the resource requirements are dynamically changed, resulting in the problem that the Physical Machine (PM) resource utilization in the network is too high or too low. To solve the above problem, the resource usage of PM in the network is divided into five different partitions, and a multi-priority VNF migration request queue scheduling model is proposed. Secondly, based on the model, a joint optimization model is established to minimize the VNF migration cost and minimize the network energy consumption. Finally, a multi-priority VNF migration cost and network energy joint optimization algorithm based on 5G access network is presented to solve the above model. The simulation results show that the algorithm can effectively improve the PM resources utilization, ensure the PM performance and balance the PM load while effectively realizing a compromise between VNF migration cost and network energy consumption.
-
表 1 MJOVME算法
输入:${\text{N}}$, ${\text{M}}$, ${\text{F}}$, ${{\text{P}}^b}$, ${u_1}$, ${u_2}$, $A$, $v_m^f$ 输出:${{\text{P}}^a}$ (1) 初始化:${{\text{P}}^a} = {{\text{P}}^b}$; (2) 确定过载区PM,设置优先级为${Q_4}$,表示为
${{\text{N}}_4} = \left\{ n_1^{{Q_4}}\;{\rm{ }}n_2^{{Q_4}}\;{\rm{ }} ·\!·\!· \; n_k^{{Q_4}}\right\} $,执行子算法2;(3) 确定高载区PM,设置优先级为${Q_3}$,表示为
${{\text{N}}_3} = \left\{ n_{k + 1}^{{Q_3}}\;{\rm{ }}n_{k + 2}^{{Q_3}}\;{\rm{ }} ·\!·\!· \;{\rm{ }}n_l^{{Q_3}}\right\} $,执行子算法2;(4) 确定低载区PM,设置优先级为${Q_1}$,表示为
${{\text{N}}_1} = \left\{ n_{l + 1}^{{Q_1}}\;{\rm{ }}n_{l + 2}^{{Q_1}}\;{\rm{ }} ·\!·\!· \;n_m^{{Q_1}}\right\} $,执行子算法3;(5) 确定轻载区PM,设置优先级为${Q_2}$,表示为
${{\text{N}}_2} = \left\{ n_{m + 1}^{{Q_2}}\;{\rm{ }}n_{m + 2}^{{Q_2}}\;{\rm{ }} ·\!·\!· \; n_n^{{Q_2}}\right\} $,执行子算法3。表 2 子算法2高负载PM消除算法
输入:高负载PM$n_j^{{Q_q}}$, ${\text{N}}$, ${\text{M}}$, ${\text{F}}$, ${{\text{P}}^a}$, $u_{n_j^{{Q_q}}}^{{\rm{cpu}}}$, $u_{n_j^{{Q_q}}}^{{\rm{mem}}}$, ${u_1}$, ${u_2}$ 输出:${{\text{P}}^a}$
(1) 创建该PM待迁移的VNF集合${\rm{VNFSET}}\left(n_j^{{Q_q}}\right) = {\rm{NULL}}$;(2) 据式(20)按值从小到大,对该PM上VNF进行排序,表示为:
${{\text{M}}_z} = \left\{ k_{m,1}^{f,l}\;{\rm{ }}k_{m,i}^{f,l}\;{\rm{ }} ·\!·\!· \;k_{m,z}^{f,l}\right\} $;(3) while $u_{n_j^{{Q_q}}}^{{\rm{cpu}}} > {u_2}$或$u_{n_j^{{Q_q}}}^{{\rm{mem}}} > {u_2}$ do (4) for $k_{m,i}^{f,l}\;(1 \le i \le z)$ do (5) if 迁移VNF$k_{m,i}^{f,l}$能够使得PM的$u_{n_j^{{Q_q}}}^{{\rm{cpu}}}$与$u_{n_j^{{Q_q}}}^{{\rm{mem}}}$均小于${u_2}$ do (6) 将VNF$k_{m,1}^{f,l}$添加到集合${\rm{VNFSET}}\left(n_j^{{Q_q}}\right)$中; (7) break; (8) end if (9) end for (10) if $i > z$ then (11) 将$k_{m,1}^{f,l}$添加到集合${\rm{VNFSET}}\left(n_j^{{Q_q}}\right)$中,同时更新集合
${{\text{M}}_z} = {{\text{M}}_z} - k_{m,1}^{f,l}$;(12) $z = z - 1$; (13) end if (14) 据式(11)、式(12)更新计算PM$n_j^{{Q_q}}$的$u_{n_j^{{Q_q}}}^{{\rm{cpu}}}$与$u_{n_j^{{Q_q}}}^{{\rm{mem}}}$; (15) end while (16) for $k_m^{f,l} \in {\rm{VNFSET}}\left(n_j^{{Q_q}}\right)$ do (17) 执行子算法4,得到迁移目标PM$n$; (18) if 子算法4返回NULL then (19) 据式(21)按值从小到大,对休眠状态的PM进行排序表
示为:${{\text{N}}_z} = \{ {n_1}\;{\rm{ }}\;{n_i}\;{\rm{ }} ·\!·\!· \;{n_z}\} $;(20) for ${n_i} \in {{\text{N}}_z}$ do (21) 据式(7)计算将VNF$k_m^{f,l}$迁移至PM${n_i}$上时,VNF$k_m^{f,l}$所
属SFC$f$的时延${D_f}$;(22) if ${D_f} < D_f^{{\rm{up}}}$ then (23) 据式(6)计算得到$B_{({n_i} - 1){n_i}}^v$与$B_{({n_i} - 1){n_i}}^v$; (24) if $B_{({n_i} - 1){n_i}}^v < {B_{({n_i} - 1){n_i}}}$且$B_{({n_i} - 1){n_i}}^v < {B_{({n_i} - 1){n_i}}}$ then (25) 将VNF$k_m^{f,l}$迁移至PM${n_i}$,同时更新${{\text{P}}^a} = {{\text{P}}^a}$; (26) break; (27) else 将$k_m^{f,l}$迁移至目的PM$n$,更新${{\text{P}}^a} = {{\text{P}}^a}$; (28) end if (29) end for (30) return ${{\text{P}}^a}$。 表 3 子算法3低负载PM整合算法
输入:低负载PM$n_j^{{Q_q}}$, ${\text{N}}$, ${\text{M}}$, ${\text{F}}$, ${{\text{P}}^a}$, $u_{n_j^{{Q_q}}}^{{\rm{cpu}}}$, $u_{n_j^{{Q_q}}}^{{\rm{mem}}}$, ${u_1}$, ${u_2}$ 输出:${{\text{P}}^a}$ (1) 据式(19)分别计算$(1 - \alpha ) \cdot C\,_n\,\!\!\!^{{\rm{mig}}}/C\,_n\,\!\!\!^{\max }$的值与$\alpha \cdot \Delta E_n^{{\rm{sum}}}/$
$\Delta E_n^{\max }$的值;(2) if $(1 - \alpha ) \cdot C\,_n\,\!\!\!^{{\rm{mig}}}/C\,_n\,\!\!\!^{\max } \ge \alpha \cdot \Delta E_n^{{\rm{sum}}}/\Delta E_{{n}}^{\max }$ then (3) return ${{\text{P}}^a}$,算法结束;//迁移开销大于等于网络能耗减
小量,整合无意义(4) end if (5) ${{\text{P}}^t} = {{\text{P}}^a}$ (6) for 每一个运行在PM$n_j^{{Q_q}}$上的$k_m^{f,l}$ do (7) 执行子算法4,得到迁移目标PM$n$,此时计划将VNF$k_m^{f,l}$
迁移至PM$n$;(8) if 子算法4返回NULL then (9) return ${{\text{P}}^a} = {{\text{P}}^t}$,算法结束;//VNF$k_m^{f,l}$无法找到目的
PM,放弃整合(10) end if (11) end for (12) 将步骤(7)中计划迁移的VNF迁移至其目的PM,更新${{\text{P}}^a}$; (13) return ${{\text{P}}^a}$。 表 4 子算法4目的PM选择算法
输入:待迁移$k_m^{f,l}$, ${{\text{N}}_{{\rm{run}}}}$, ${u_1}$, ${u_2}$ 输出:目的PM$n$ (1) 据式(11)、式(12)计算${{\text{N}}_{{\rm{run}}}}$中各PM的CPU利用率$u_n^{{\rm{cpu}}}$和内存
利用率$u_n^{{\rm{mem}}}$,并根据${\rm{sum}}_n^u$值依次从大到小重新排列${{\text{N}}_{{\rm{run}}}}$中PM
的顺序;//${\rm{su}}{{\rm{m}}^u} = u_n^{{\rm{cpu}}} + u_n^{{\rm{mem}}}$(2) for $n \in {{\text{N}}_{{\rm{run}}}}$ do (3) 据式(11)、式(12)计算将VNF$k_m^{f,l}$迁移至PM$n$上时,PM$n$的
$u_n^{{\rm{cpu}}}$与$u_n^{{\rm{mem}}}$;(4) if ${u_1} < u_n^{{\rm{cpu}}} < {u_2}$且${u_1} < u_n^{{\rm{mem}}} < {u_2}$ then (5) 据式(7)计算将VNF$k_m^{f,l}$迁移至PM$n$上时,VNF$k_m^{f,l}$所属
SFC$f$的时延${D_f}$;(6) if ${D_f} < D_f^{{\rm{up}}}$ then (7) 据式(6)计算得到$B_{(n - 1)n}^v$与$B_{n(n + 1)}^v$; (8) if $B_{(n - 1)n}^v < {B_{(n - 1)n}}$且$B_{n(n + 1)}^v < {B_{n(n + 1)}}$ then (9) return 目的PM$n$; (10) break; (11) end if (12) end if (13) end if (14) end for (15) if 步骤(9)未执行 then (16) return NULL。 (17) end if 表 5 基础设施中PM节点的参数设置
参数 数值 PM个数 200, 230, 260 ${M_n}$ (GB) {4, 8, 12, 16} $P_n^{{\rm{ba}}}$ (W) Uniform[90, 120] ${d_{nl}}$(ms) Uniform[1, 2] $P_n^{{\rm{mc}}}$ (W) Uniform[170, 230] ${B_{nl}}$ (Mbps) Uniform[80, 100] $P_n^{{\rm{sl}}}$ (W) Uniform[25, 35] ${u_{\rm{1}}}$ 0.9 ${C_n}$ (MIPS) Uniform[200, 300] ${u_{\rm{2}}}$ 0.3 表 6 VNF相关参数设置
参数 数值 VNF种类 8 ${r_{{\rm{mem}}}}$ (GB/Mbps) 4 $v_m^f$ (Mbps) Uniform[0.1, 1.0] $D$ (Mb) 0.0005 ${r_{{\rm{cpu}}}}$ (MIPS/ Mbps) 110 $A$ 100 表 7 SFC相关参数设置
参数 数值 SFC请求数量 60, 70, 80 $D_f^{{\rm{up}}}$ (ms) [8, 10, 12] VNF集合长度 Uniform[3, 5](种类随机) 链路所需带宽资源 (Mbps) Uniform[5, 10] -
BOURAS C, KOLLIA A, and PAPAZOIS A. SDN & NFV in 5G: Advancements and challenges[C]. 2017 20th Conference on Innovations in Clouds, Internet and Networks (ICIN), Paris, France, 2017: 107–111. LI Defang, HONG Peilin, XUE Kaiping, et al. Virtual network function placement considering resource optimization and SFC requests in cloud datacenter[J]. IEEE Transactions on Parallel and Distributed Systems, 2018, 29(7): 1664–1677. doi: 10.1109/TPDS.2018.2802518 ZHANG Jie, ZENG Deze, GU Lin, et al. Joint optimization of virtual function migration and rule update in software defined NFV networks[C]. GLOBECOM 2017-2017 IEEE Global Communications Conference, Singapore, 2018: 1–5. CHO D, TAHERI J, ZOMAYA A Y, et al. Real-time virtual network function (VNF) migration toward low network latency in cloud environments[C]. 2017 10th International Conference on Cloud Computing (CLOUD), Honolulu, USA, 2017: 798–801. ERAMO V, AMMAR M, and LAVACCA F G. Migration energy aware reconfigurations of virtual network function instances in NFV architectures[J]. IEEE Access, 2017, 5: 4927–4938. doi: 10.1109/ACCESS.2017.2685437 ERAMO V, MIUCCI E, AMMAR M, et al. An approach for service function chain routing and virtual function network instance migration in network function virtualization architectures[J]. IEEE/ACM Transactions on Networking, 2017, 25(4): 2008–2025. doi: 10.1109/TNET.2017.2668470 ZHANG Jinshi, LI Liang, and WANG Dong. Optimizing VNF live migration via para-virtualization driver and QuickAssist technology[C]. 2017 IEEE International Conference on Communications (ICC), Paris, France, 2017: 1–6. TANG Lun, YANG Heng, MA Runlin, et al. Queue-aware dynamic placement of virtual network functions in 5G access network[J]. IEEE Access, 2018, 6: 44291–44305. doi: 10.1109/ACCESS.2018.2862632 XIA Jing, CAI Zhiping, and XU Ming. Optimized virtual network functions migration for NFV[C]. 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), Wuhan, China, 2016: 340–346. LIN Tachun, ZHOU Zhili, TORNATORE M, et al. Demand-aware network function placement[J]. Journal of Lightwave Technology, 2016, 34(11): 2590–2600. doi: 10.1109/JLT.2016.2535401 FAN Qiang, ANSARI N, and SUN Xiang. Energy driven avatar migration in green cloudlet networks[J]. IEEE Communications Letters, 2017, 21(7): 1601–1604. doi: 10.1109/LCOMM.2017.2684812 XU Heyang and YANG Bo. Energy-aware resource management in cloud computing considering load balance[J]. Journal of Information Science and Engineering, 2017, 33(1): 1–16. doi: 10.6688/JISE.2017.33.1.1 MIJUMBI R, SERRAT J, GORRICHO J L, et al. Design and evaluation of algorithms for mapping and scheduling of virtual network functions[C]. The 1st IEEE Conference on Network Softwarization (NetSoft), London, UK, 2015: 1–9. -





 下载:
下载:



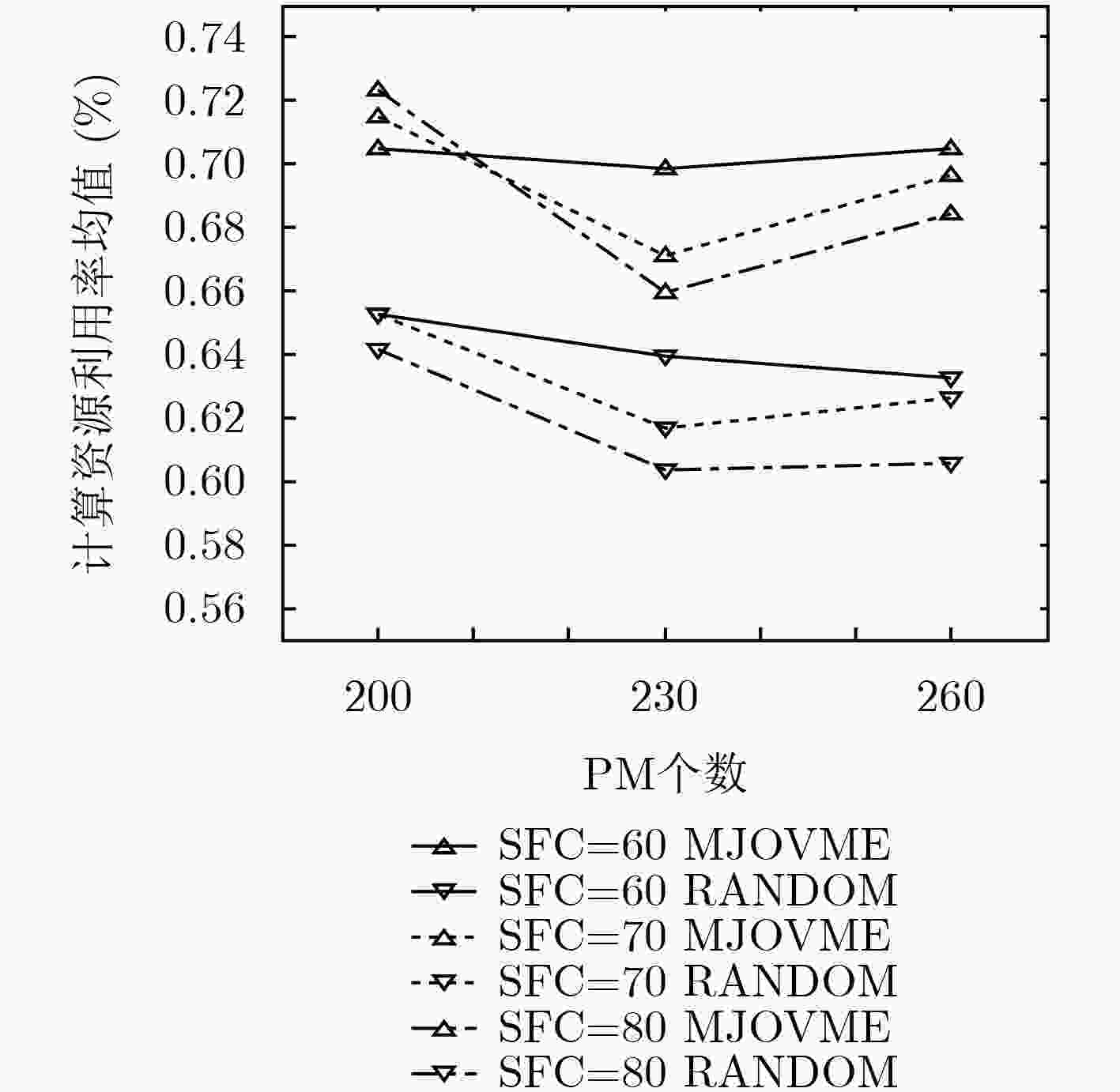
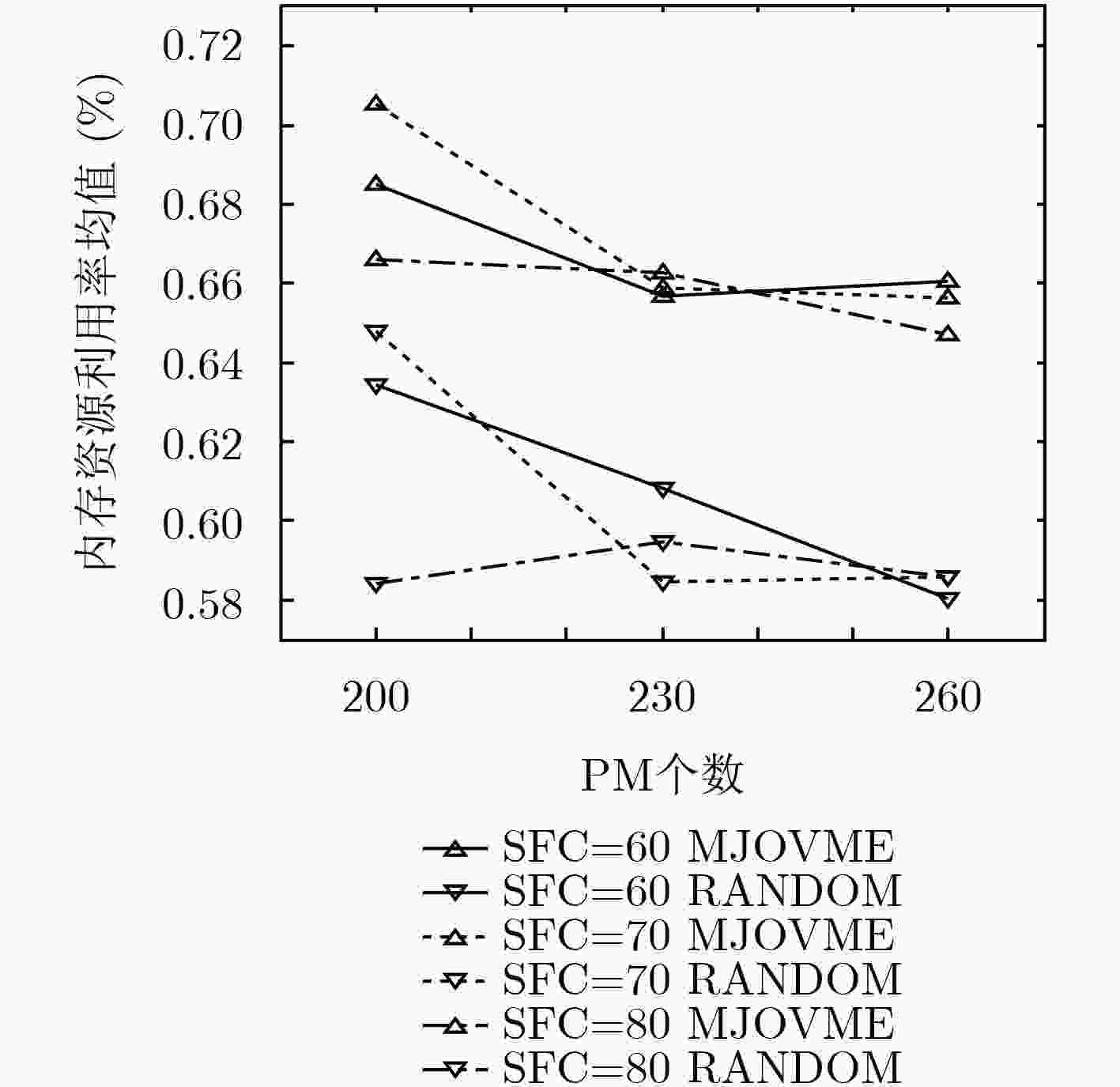
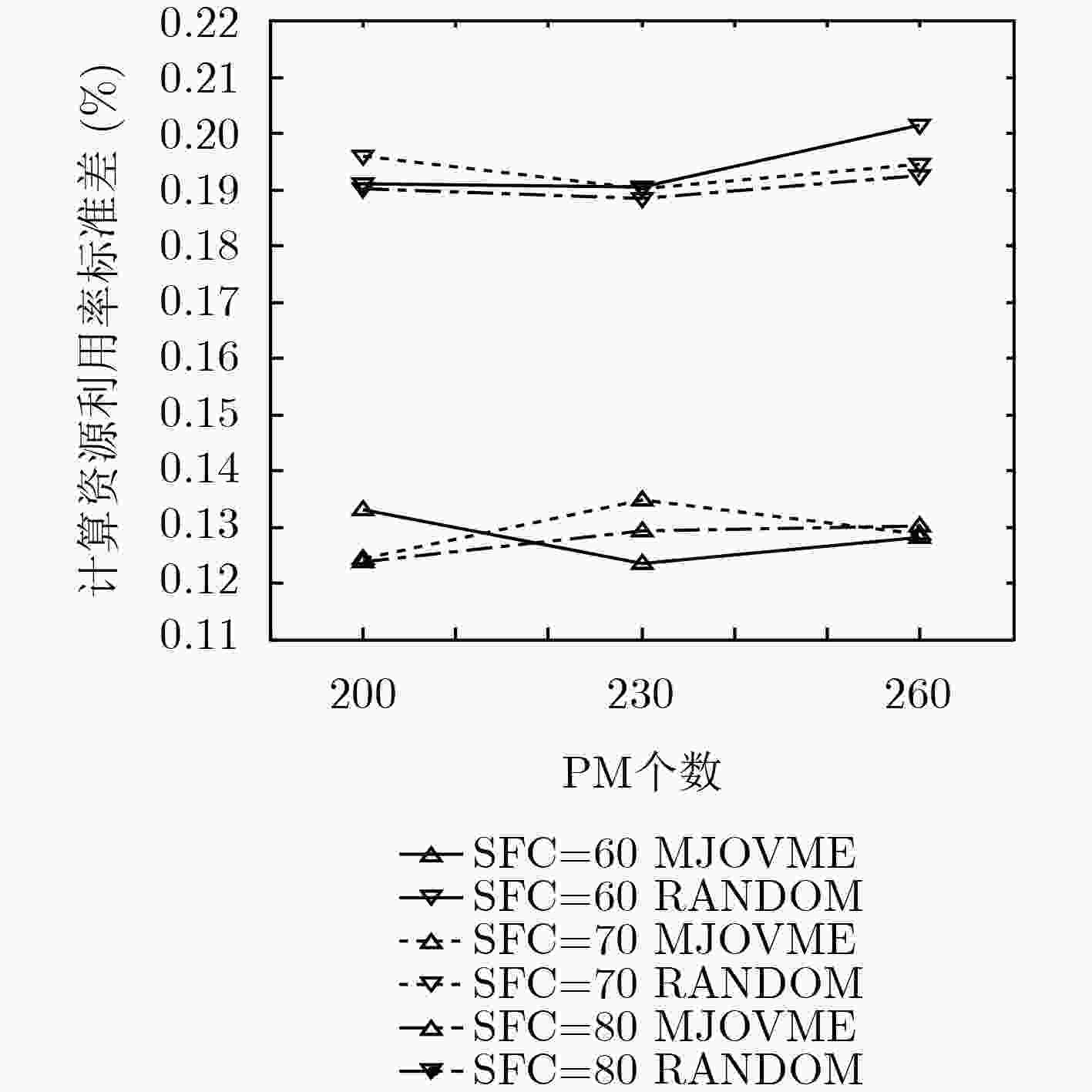
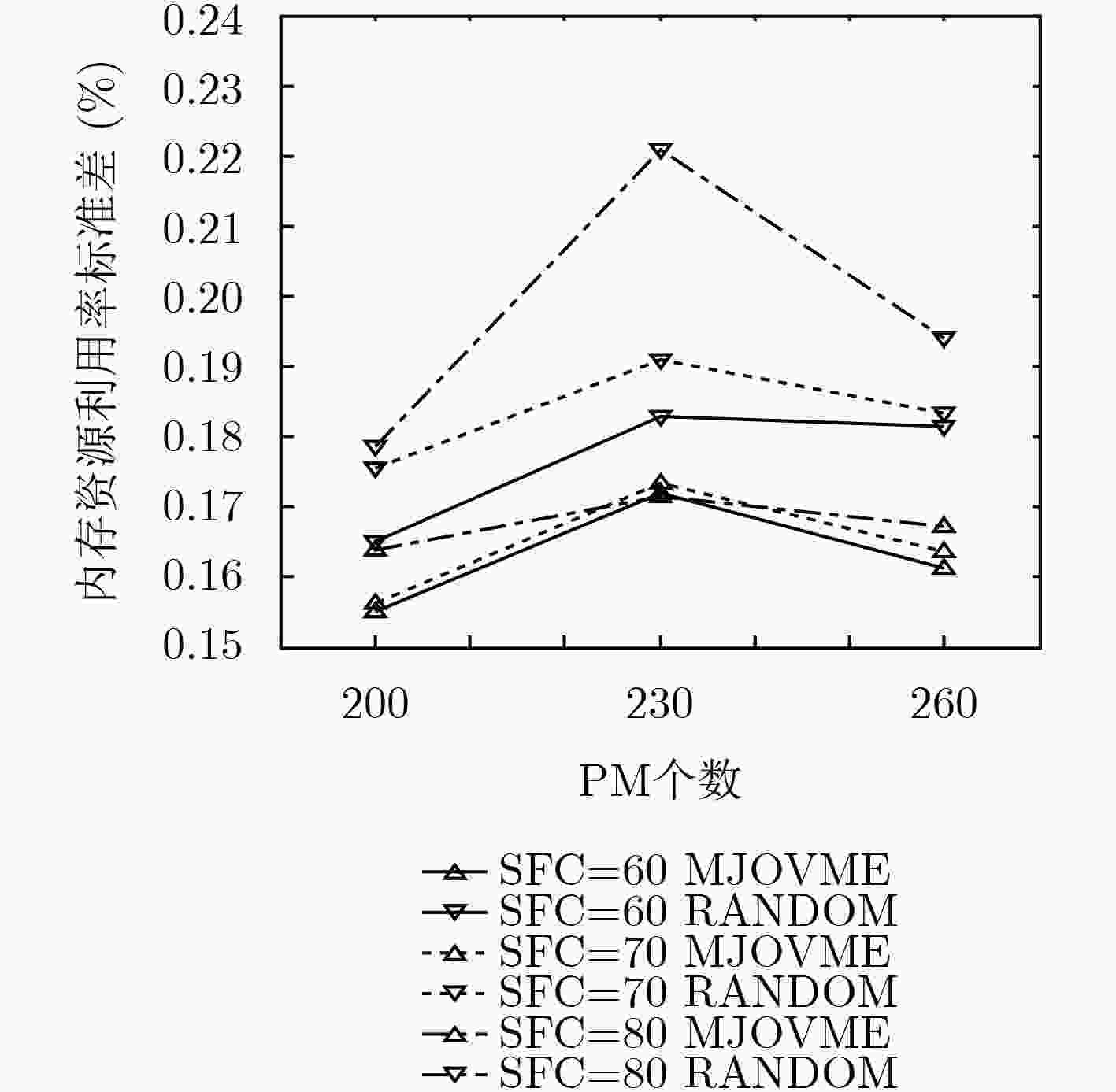


 下载:
下载:
