一种侧信道风险感知的虚拟节点迁移方法

黄开枝; 潘启润; 袁泉; 游伟

doi:10.11999/JEIT180905

一种侧信道风险感知的虚拟节点迁移方法

doi: 10.11999/JEIT180905

国家数字交换系统工程技术研究中心郑州 450002

基金项目: 国家重点研发计划网络空间安全专项(2016YFB0801605)，国家自然科学基金创新群体项目(61521003)

详细信息

作者简介:
黄开枝：女，1973年生，教授，博士生导师，研究方向为移动通信、无线物理层安全

潘启润：女，1993年生，硕士生，研究方向为新一代移动通信技术、网络切片

袁泉：男，1991年生，博士生，研究方向为移动通信网络、网络功能虚拟化

游伟：男，1984年生，讲师，研究方向为密码学、5G网络安全

通讯作者:
潘启润　panqirun03@163.com

中图分类号: TP393
计量
- 文章访问数: 1998
- HTML全文浏览量: 979
- PDF下载量: 80
- 被引次数: 0
出版历程
- 收稿日期: 2018-09-20
- 修回日期: 2019-02-26
- 网络出版日期: 2019-03-11
- 刊出日期: 2019-09-10

A Virtual Node Migration Method for Sensing Side-channel Risk

National Digital Switching System Engineering and Technological R&D Center, Zhengzhou 450002, China

Funds: The National Key R & D Program Cyberspace Security Special (2016YFB0801605), The National Natural Science Foundation Innovative Groups Project of China (61521003)

摘要

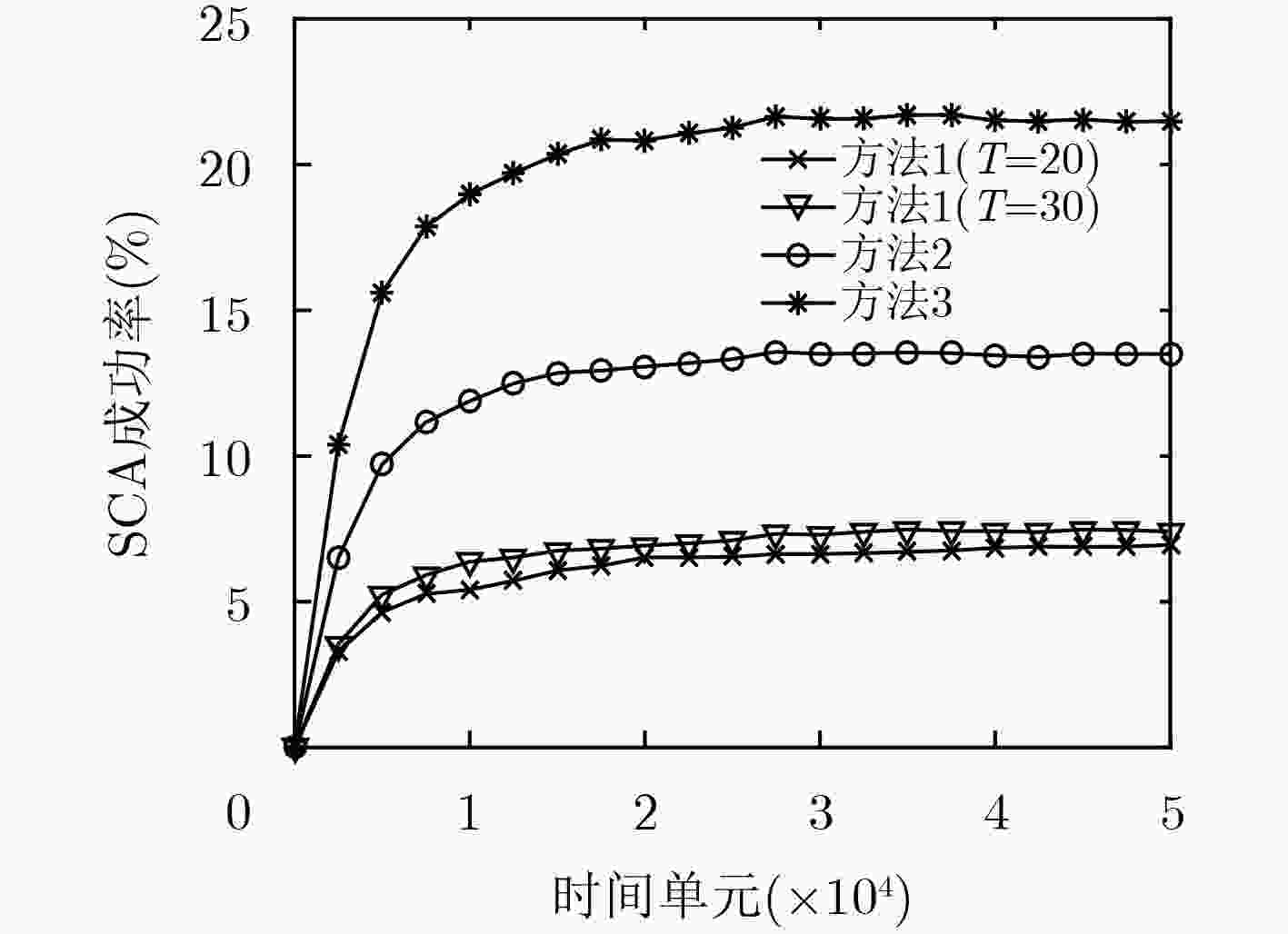
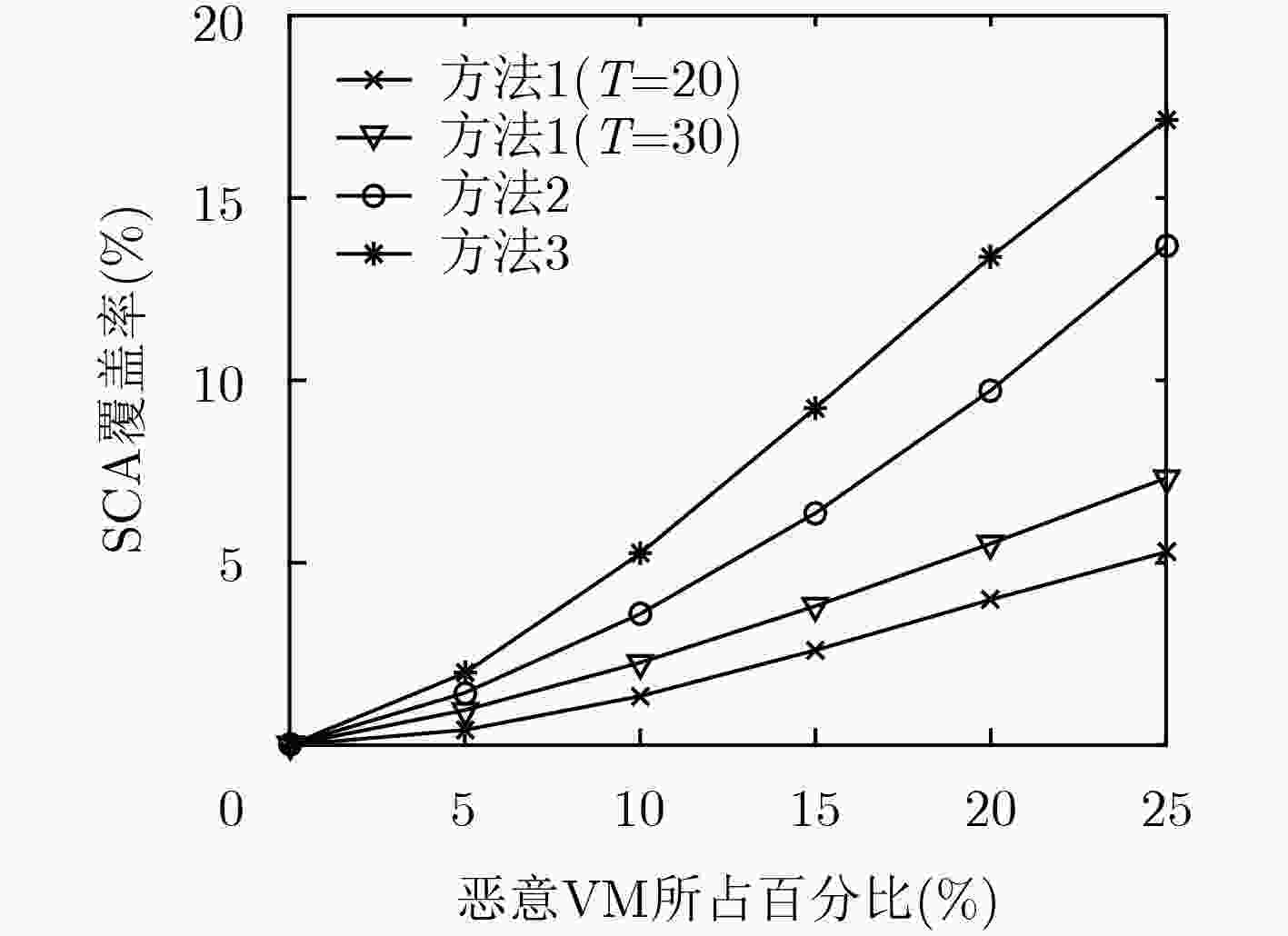
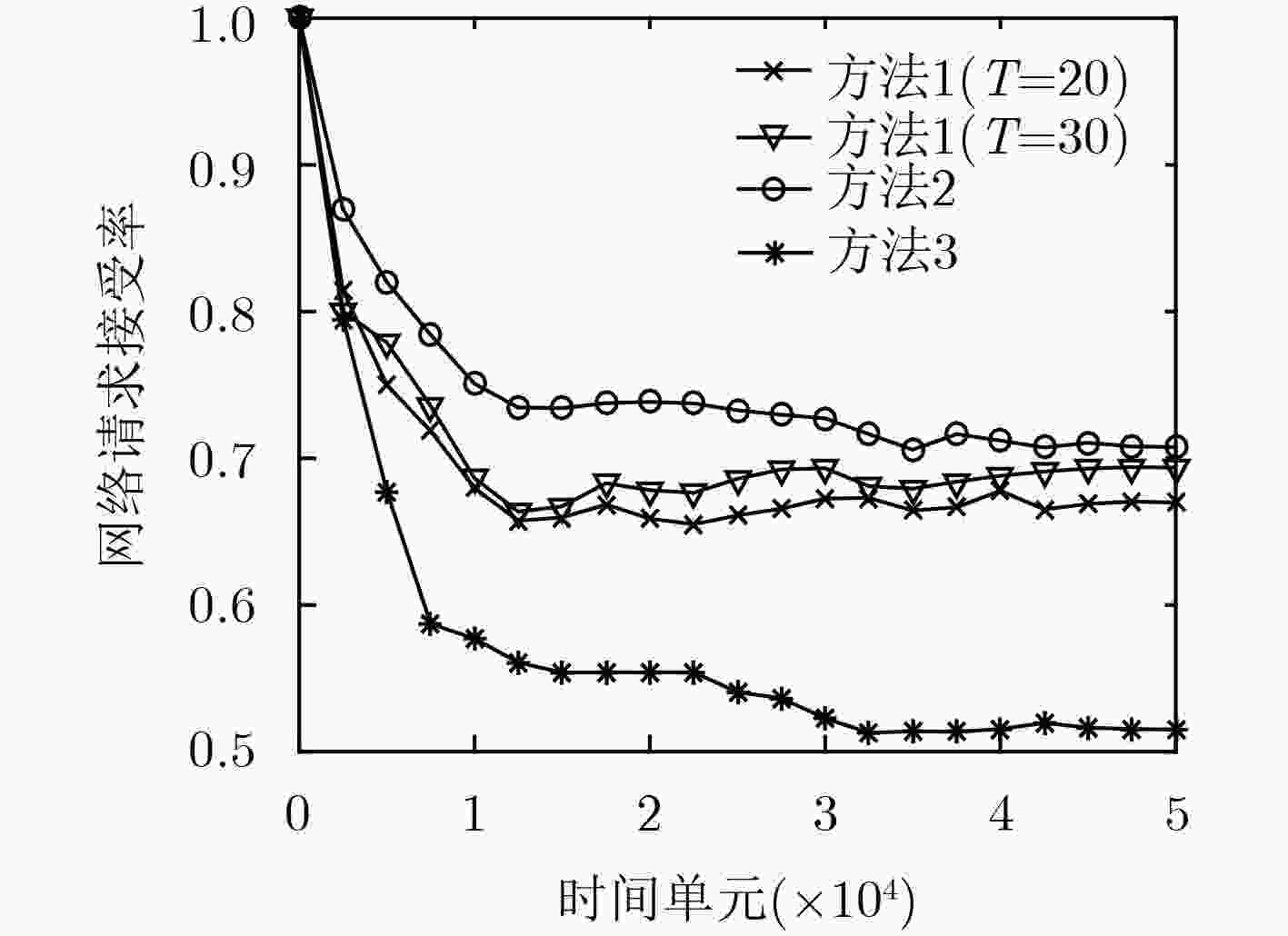
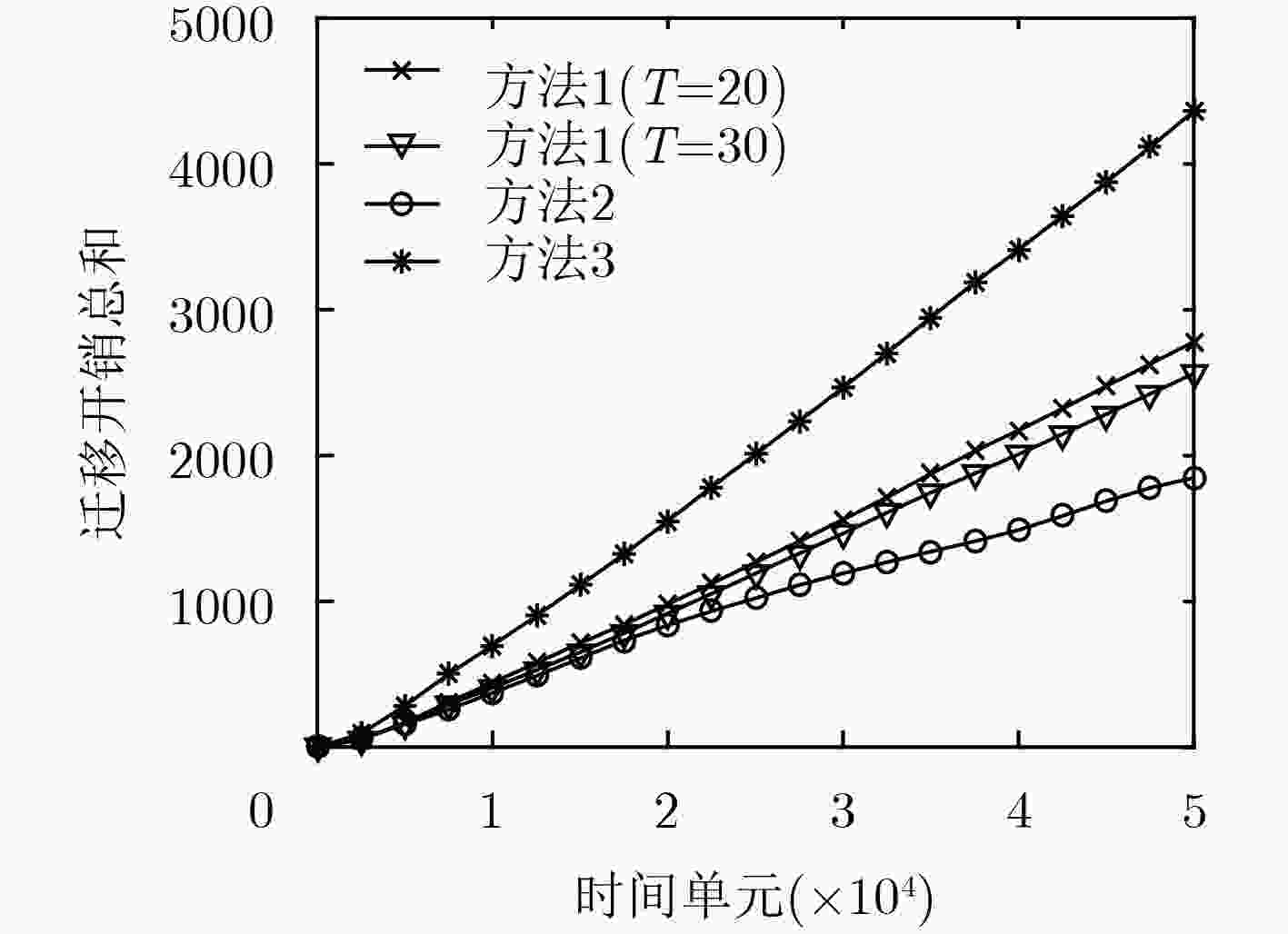
摘要: 为防御网络切片(NS)中的侧信道攻击(SCA)，现有的基于动态迁移的防御方法存在不同虚拟节点共享物理资源的条件过于松弛的问题。该文提出一种侧信道风险感知的虚拟节点迁移方法。根据侧信道攻击的实施特点，结合熵值法对虚拟节点的侧信道风险进行评估，并将服务器上偏离平均风险程度大的虚拟节点进行迁移；采用马尔科夫决策过程描述网络切片虚拟节点的迁移问题，并使用Sarsa学习算法求解出最终的迁移结果。仿真结果表明，该方法将恶意网络切片实例与其他网络切片实例隔离开，达到防御侧信道攻击的目的。
- 网络切片 /
- 安全隔离 /
- 侧信道攻击 /
- 马尔可夫决策过程 /
- Sarsa学习算法
Abstract: In order to defend against Side-Channel Attacks (SCA) in Network Slicing (NS), the existing defense methods based on dynamic migration have the problem that the conditions for sharing of physical resources between different virtual nodes are not strict enough, a virtual node migration method is proposed for sensing side-channel risk. According to the characteristics of SCA, the entropy method is used to evaluate the side-channel risks and migrate the virtual node from a server with large deviation from average risk. The Markov decision process is used to describe the migration of virtual nodes for network slicing, and the Sarsa learning algorithm is used to solve the optimal migration scheme. The simulation results show that this method can separates malicious network slice instances from other target network slice instances to achieve the purpose of defense side channel attacks.
- Network Slicing (NS) /
- Security isolation /
- Side-Channel Attacks (SCA) /
- Markov decision process /
- Sarsa algorithm

HTML全文

图 1 NSI宏观示意图

下载: 全尺寸图片幻灯片

图 2 NSI部署图及侧信道攻击

下载: 全尺寸图片幻灯片

图 3 增强学习原理图

下载: 全尺寸图片幻灯片

图 4 t时刻网络视图

下载: 全尺寸图片幻灯片

图 5 侧信道攻击成功率比较

下载: 全尺寸图片幻灯片

图 6 侧信道攻击覆盖率比较

下载: 全尺寸图片幻灯片

图 7 网络请求接受率比较

下载: 全尺寸图片幻灯片

图 8 迁移开销总和比较

下载: 全尺寸图片幻灯片

表 1 影响安全参数

符号	含义
$\omega $	隐私信息泄露速率
$\theta $	共存时间
${\mu _{\min }}$	信息被成功窃取的最小信息量

下载: 导出CSV

表 2 算法1

输入：${G_{\rm S}} = \left( {{N_{\rm S}}, {L_{\rm S}}, {C_{\rm N}}, {L_{\rm N}}} \right)$；$G_{\rm V}^k = \left( {N_{\rm V}^k, L_{\rm V}^k, R_{\rm N}^k, R_{\rm L}^k} \right)$；观测周　　　　期$T\;$；观测间隔$\lambda $；SCA风险阈值$\text{Γ}$
输出：最终迁移结果${M^k} = \left\{ {M_{\rm N}^k, M_{\rm L}^k} \right\}$
(1) for all $n_v^k \in N_{\rm V}^k$ do
(2) for all $m \in \left[ {1, {T / \lambda }} \right]$ do //在观测周期$T\;$内，获取${T / \lambda }$个观测数　　值；
(3) $Y_{n_v^k \mapsto {n_s}}^m = \left\{ {f_k^m, v_k^m\left( {{n_s}} \right), \eta _k^m\left( {n_v^k} \right)} \right\}, 1 \le m \le {T/ \lambda }$，　　　${Y_{n_v^k \mapsto {n_s}}} = \left( {\begin{array}{*{20}{c}} {{Y_{n_v^k \mapsto {n_s}}}} \\ {Y_{n_v^k \mapsto {n_s}}^m} \end{array}} \right)$；
(4) end for
(5) ${Z_{n_v^k \mapsto {n_s}}} = {\rm{RDV}}\left( {{Y_{n_v^k \mapsto {n_s}}}, {T / \lambda }} \right)$//调用算法2(见表3)求出SCA风险值；
(6) end for
(7) 获取$N_{\rm V}^k$所映射到的服务器集合$U_{\rm S}^k$；
(8) for all ${n_s} \in U_{\rm S}^k$ do
(9) 计算SCA风险值的平均值E和方差${{D}}\left( {Z\left( {{n_s}, {T_n}} \right)} \right)$；
(10) if ${{D}}\left( {Z\left( {{n_s}, {T_n}} \right)} \right) \ge \text{Γ} $ do
(11) 计算${n_s}$上所有VM的风险值与均值之差，将差值最大的　　　VM加入待迁移VM集合$\varOmega $中；
(12) end if
(13) end for
(14) $M_{\rm N}^k = {\rm{SARSA}}\left( {\varOmega , U_{\rm S}^k, {G_{\rm S}}} \right)$//调用算法3(见表4)求出VM的　　　迁移结果；
(15) for all $n_v^k \in \varOmega $ do //采用k短路径算法进行相关链路映射；
(16) for all $\chi$$ \in \left\{ {n_v^k} {\text{所有相邻节点}}\right\}$ do
(17) 获取$n_v^k$和$\chi $所部署的服务器，分别为$n_s^\sigma $和$n_s^\chi $，并求出二者　　　之间最短路径跳数hp；
(18) 利用k短路径算法求出$n_s^\sigma $到$n_s^\chi $且跳数为hp的路径；
(19) if ${r_{{\rm{bw}}}}\left( {n_v^k, \chi } \right) \le \min \left\{ {{c_{{\rm{bw}}}}\left( {n_s^\sigma , n_s^1} \right), ·\!·\!· , {c_{{\rm{bw}}}}\left( {n_s^{{\rm{hp}} - 1}, n_s^\chi } \right)} \right\}$ do
(20) 将${l_v}\left( {n_v^k, \chi } \right)$映射到物理链路${l_{n_s^\sigma \to {n_s} \to n_s^\chi }}$上，结果存入$M_{\rm L}^k$；
(21) else do hp=hp+1，go to line 19；end if
(22) end for
(23) end for
(24) 返回最终迁移结果${M^k} = \left\{ {M_N^k, M_L^k} \right\}$。

下载: 导出CSV

表 3 基于熵值法的VM的SCA风险值求解算法(RDV)(算法2)

输入：${Y_{n_v^k \mapsto {n_s}}}$；${T / \lambda }$
输出：${Z_{n_v^k \mapsto {n_s}}}$
(1) ${\varphi _{ij}} = {Y_{n_v^k \mapsto {n_s}}}$，归一化处理$\varphi $，得到$\varphi _{ij}'$；
(2) if $1 \le j \le 3$ do 利用式(2)计算$\varphi _{ij}'$的比重${p_{ij}}$；end if
(3) if $1 \le j \le 3$ do 利用式(3)计算第j项指标的熵值${e_j}$；end if
(4) if $1 \le j \le 3$ do 利用式(4)计算第j项指标的权重${w_j}$；end if
(5) ${Z_{n_v^k \mapsto {n_s}}} = \displaystyle\sum\nolimits_{j = 1}^3 {{w_j}\left( {\frac{1}{{T/\lambda }}\displaystyle\sum\nolimits_{i = 1}^{T/\lambda } {\varphi {'_{ij}}} } \right)} $，并返回该值。

下载: 导出CSV

表 4 基于Sarsa算法的VM迁移算法 (SARSA)(算法3)

输入：$\varOmega $；$U_{\rm S}^k$；${G_{\rm S}}$
输出：$M_{\rm N}^k$
(1) 根据$\varOmega $初始化MDP的状态空间S，初始化行为空间A，设定　　　学习因子${\alpha _0}$和折扣因子$\gamma $；
(2) 令t=0，随机初始化起始状态${s_0}$，并在空间A中随机选择行为　　　${a_0}$；
(3) if $1 \le m \le {W_{\max }}$ do //${W_{\max }}$为最大循环次数
(4) 观测下一时刻状态${s_{t + 1}}$，根据行为选择策略${{\text{π}} _Q}$决定时刻　　　t+1的行为${a_{t + 1}}$；
(5) 根据式(9)计算服务器SCA风险差异值，得到收益函数瞬时值　　　$r({s_t}, {a_t})$；
(6) 根据迭代式(10)更新当前行为值函数$Q({s_t}, {a_t})$；
(7) 令t=t+1，根据行为选择策略${{\text{π}} _Q}$决定时刻t的行为${a_t}$；
(8) if ${Q^} < Q({s_t}, {a_t})$ do ${Q^} = Q({s_t}, {a_t})$ end if
(9) end if
(10) 根据${Q^*}$获得最终的迁移方案$M_{\rm N}^k$，并返回该值。

下载: 导出CSV

表 5 仿真参数

参数	物理网络	网络切片实例
网络模型	Waxman	纯随机
节点连接概率p	$0.2{\operatorname{e} ^{ - d/\left( {0.5 \times 141} \right)}}$	0.2
节点个数	100	服从U(2, 10)
节点和链路资源容量	服从U(50, 100)	服从U(1, 20)

下载: 导出CSV

参考文献(19)

NGMN Alliance. 5G white paper[EB/OL]. https://www.ngmn.org/5g-white-paper/5g-white-paper.html, 2015.

WANG Zhiming, WU Jiangxing, GUO Zehua, et al. Secure virtual network embedding to mitigate the risk of covert channel attacks[C]. 2016 IEEE Conference on Computer Communications Workshops, San Francisco, USA, 2016: 144–145.

RISTENPART T, TROMER E, SHACHAM H, et al. Hey, you, get off of my cloud: Exploring information leakage in third-party compute clouds[C]. The 16th ACM Conference on Computer and Communications Security, Chicago, USA, 2009: 199–212.

GULMEZOGLU B, İNCI M S, IRAZOQUI G, et al. Cross-VM cache attacks on AES[J]. IEEE Transactions on Multi-Scale Computing Systems, 2016, 2(3): 211–222. doi: 10.1109/tmscs.2016.2550438

OKAMURA K and OYAMA Y. Load-based covert channels between Xen virtual machines[C]. 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 2010: 173–180.

YU Si, GUI Xiaolin, and LIN Jiancai. An approach with two-stage mode to detect cache-based side channel attacks[C]. 2013 International Conference on Information Networking, Bangkok, Thailand, 2013: 186–191.

WANG Lina, LIU Weijie, KUMAR N, et al. A novel covert channel detection method in cloud based on XSRM and improved event association algorithm[J]. Security and Communication Networks, 2016, 9(16): 3543–3557. doi: 10.1002/sec.1560

WANG Zhenghong and LEE R B. A novel cache architecture with enhanced performance and security[C]. The 41st Annual IEEE/ACM International Symposium on Microarchitecture, Lake Como, Italy, 2008: 83–93.

PATTUK E, KANTARCIOGLU M, LIN Zhiqiang, et al. Preventing cryptographic key leakage in cloud virtual machines[C]. The 23rd Usenix Conference on Security Symposium, San Diego, USA, 2014: 703–718.

HAN Yi, CHAN J, ALPCAN T, et al. Using virtual machine allocation policies to defend against co-resident attacks in cloud computing[J]. IEEE Transactions on Dependable and Secure Computing, 2017, 14(1): 95–108. doi: 10.1109/tdsc.2015.2429132

ADILI M T, MOHAMMADI A, MANSHAEI M H, et al. A cost-effective security management for clouds: A game-theoretic deception mechanism[C]. 2017 IFIP/IEEE Symposium on Integrated Network and Service Management (IM), Lisbon, Portugal, 2017: 98–106.

赵硕, 季新生, 毛宇星, 等. 基于安全等级的虚拟机动态迁移方法[J]. 通信学报, 2017, 38(7): 165–174. doi: 10.11959/j.issn.1000-436x.2017091

ZHAO Shuo, JI Xinsheng, MAO Yuxing, et al. Research on dynamic migration of virtual machine based on security level[J]. Journal on Communications, 2017, 38(7): 165–174. doi: 10.11959/j.issn.1000-436x.2017091

YU Si, GUI Xiaolin, LIN Jiancai, et al. A security-awareness virtual machine management scheme based on Chinese wall policy in cloud computing[J]. The Scientific World Journal, 2014, 2014: 805923. doi: 10.1155/2014/805923

桂小林, 余思, 黄汝维, 等. 一种面向云计算环境侧通道攻击防御的虚拟机部署方法[P]. 中国, 102571746, 2012.

GUI Xiaolin, YU Si, HUANG Ruwei, et al. Virtual machine deployment method oriented to side channel attack defense of cloud computation environment[P]. CN, 102571746, 2012.

LIANG Xin, GUI Xiaolin, JIAN A N, et al. Mitigating cloud co-resident attacks via grouping-based virtual machine placement strategy[C]. The 36th IEEE International Performance Computing and Communications Conference, San Diego, USA, 2017: 1–8.

ANWAR A H, ATIA G, GUIRGUIS M. It’s time to migrate! A game-theoretic framework for protecting a multi-tenant cloud against collocation attacks[C]. The 11th IEEE International Conference on Cloud Computing, San Francisco, USA, 2018: 725–731.

ALJAZZAR H and LEUE S. K*: A heuristic search algorithm for finding the k shortest paths[J]. Artificial Intelligence, 2011, 175(18): 2129–2154. doi: 10.1016/j.artint.2011.07.003

GILLANI F, AL-SHAER E, LO S, et al. Agile virtualized infrastructure to proactively defend against cyber attacks[C]. 2015 IEEE Conference on Computer Communications, Hong Kong, China, 2015: 729–737.

GONG Long, WEN Yonggang, ZHU Zuqing, et al. Toward profit-seeking virtual network embedding algorithm via global resource capacity[C]. IEEE Conference on Computer Communications, Toronto, Canada, 2014: 1–9.

施引文献

资源附件(0)

访问统计