A Classifier Learning Method Based on Tree-Augmented Naïve Bayes
-
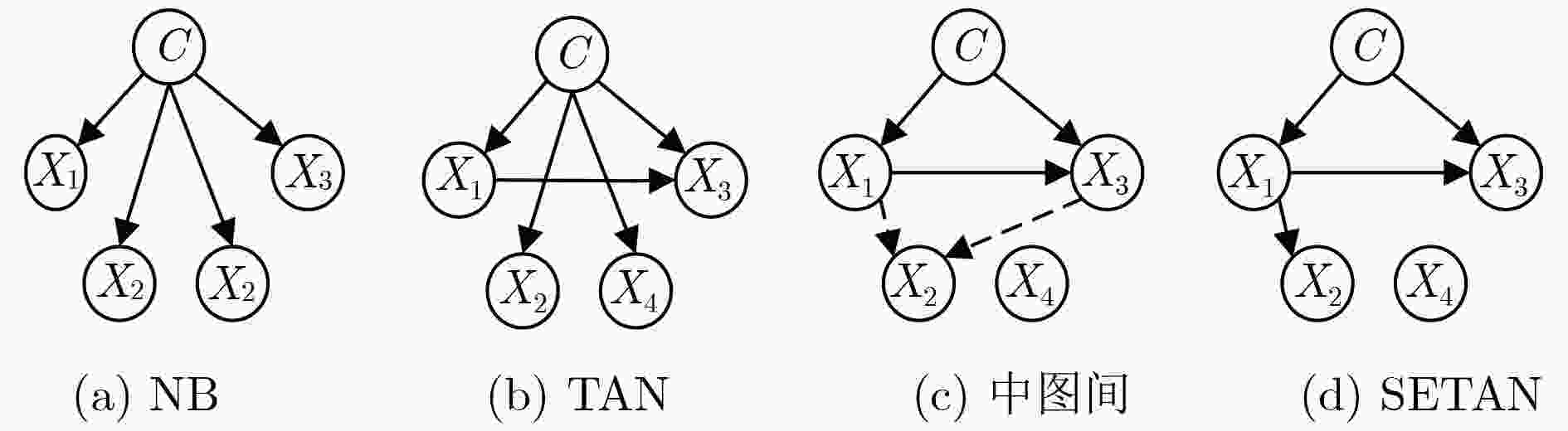
摘要: 树增强朴素贝叶斯(TAN)结构强制每个属性结点必须拥有类别父结点和一个属性父结点,也没有考虑到各个属性与类别之间的相关性差异,导致分类准确率较差。为了改进TAN的分类准确率,该文首先扩展TAN结构,允许属性结点没有父结点或只有一个属性父结点;提出一种利用可分解的评分函数构建树形贝叶斯分类模型的学习方法,采用低阶条件独立性(CI)测试初步剔除无效属性,再结合改进的贝叶斯信息标准(BIC)评分函数利用贪婪搜索获得每个属性结点的父结点,从而建立分类模型。对比朴素贝叶斯(NB)和TAN,构建的分类器在多个分类指标上表现更好,说明该方法具有一定的优越性。Abstract: The structure of Tree-Augmented Naïve Bayes (TAN) forces each attribute node to have a class node and a attribute node as parent, which results in poor classification accuracy without considering correlation between each attribute node and the class node. In order to improve the classification accuracy of TAN, firstly, the TAN structure is proposed that allows each attribute node to have no parent or only one attribute node as parent. Then, a learning method of building the tree-like Bayesian classifier using a decomposable scoring function is proposed. Finally, the low-order Conditional Independency (CI) test is applied to eliminating the useless attribute, and then based on improved Bayesian Information Criterion (BIC) function, the classification model with acquired the parent node of each attribute node is established using the greedy algorithm. Through comprehensive experiments, the proposed classifier outperforms Naïve Bayes (NB) and TAN on multiple classification, and the results prove that this learning method has certain advantages.
-
Key words:
- Bayesian classifier /
- Tree-Augmented Naïve Bayes (TAN) /
- Scoring function
-
表 1 算法描述
输入:变量集V,样本数据集D 输出:SETAN结构 步骤1 For each $X_i \in V\;$, $I(C,X_i) = {\rm{Calc\_MI}}(C,X_i)$# 计算属性
与类别之间的互信息值步骤2 将每个互信息值$I(C,X_i)$存入数组,降序 步骤3 For each $I(C,X_i) > \varepsilon $ in List $S_1 = S_1 \cup \{ X_i\} $ Add path $C - X_i$to graph $E$# 若无连接边,则添加类
别C到属性$X_i$的连接边$S_2 = S_{\rm{2}} \cup \{ X_j\} $,$X_j \in \{ I(C,X_j) < \varepsilon \} $ Add path $X_i - X_j$to graph $E$# 互信息值小于阈值$\varepsilon $的
结点则被添加到集合$S_2$Remove $I(C,X_i)$from List End for 步骤4 For each $E' \in E$ ${\rm{Score}}(E') = {\rm{Calc\_BIC}}(E')$# 计算改进的BIC评分 K2-Search of the optimal SETAN Structure # 利用评
分函数搜索最优结构End for 步骤5 Return $G = (V',E')$with best BIC score 表 2 网络结构学习实验结果
$\xi $ Asia网 Alarm网 A D R A D R 0.01 0 3 5 0 20 25 0.001 1 1 7 3 2 45 0.0001 3 0 8 15 3 45 表 3 实验数据集信息
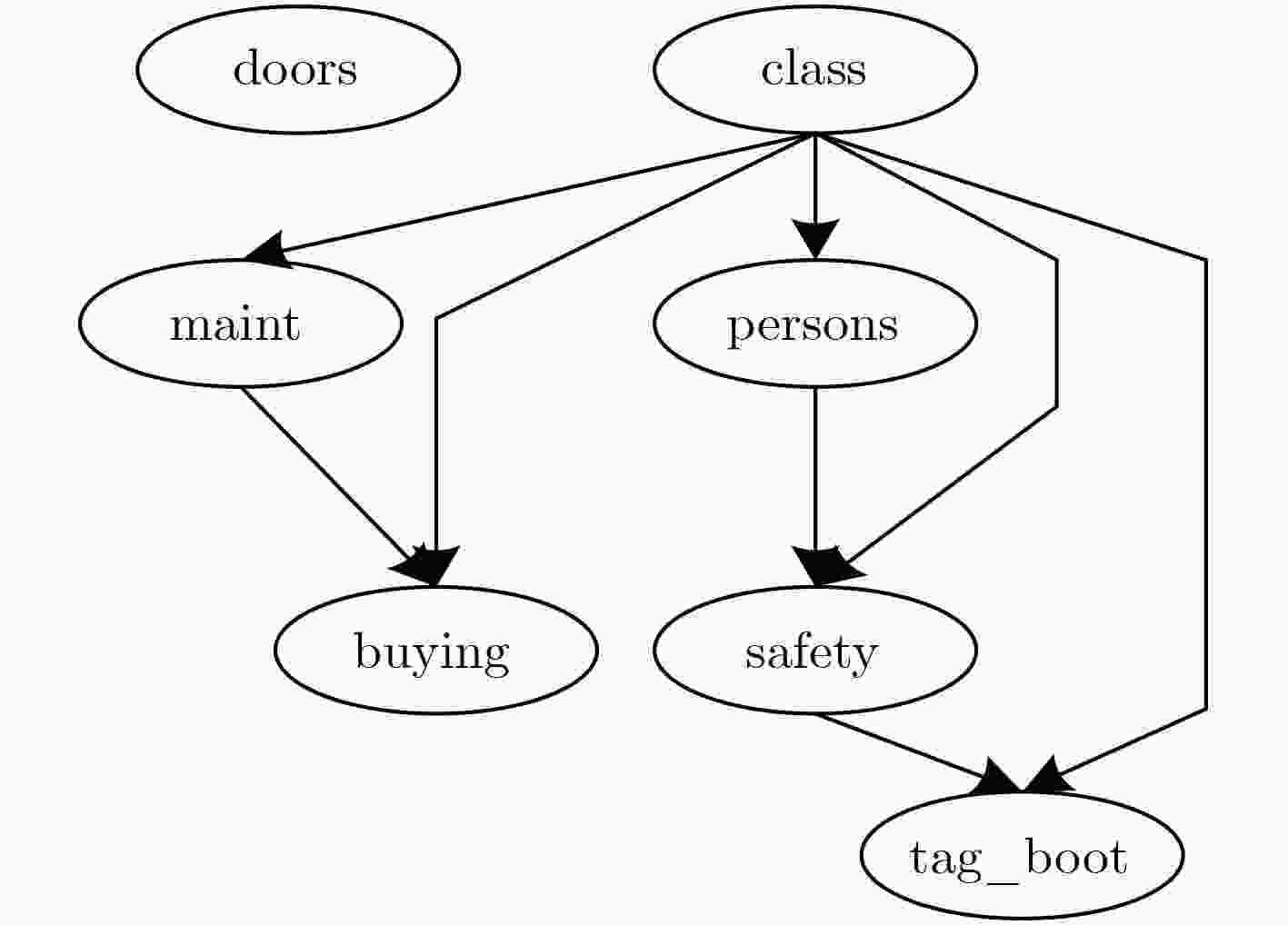
数据集 样本数量 类别分布 属性数量 分类数量 缺失值 Balance 625 49/288/288 4 3 否 Car 1728 1210/384/69/65 6 4 否 Connect 67558 44473/16635/6449 42 3 否 Mushroom 8124 4208/3916 22 2 是 Nursery 12960 4320/2/328/4266/4044 8 5 否 SPECT 80 40/40 22 2 否 Cancer 286 85/201 9 2 否 Votes 435 168/267 16 2 是 表 4 阈值
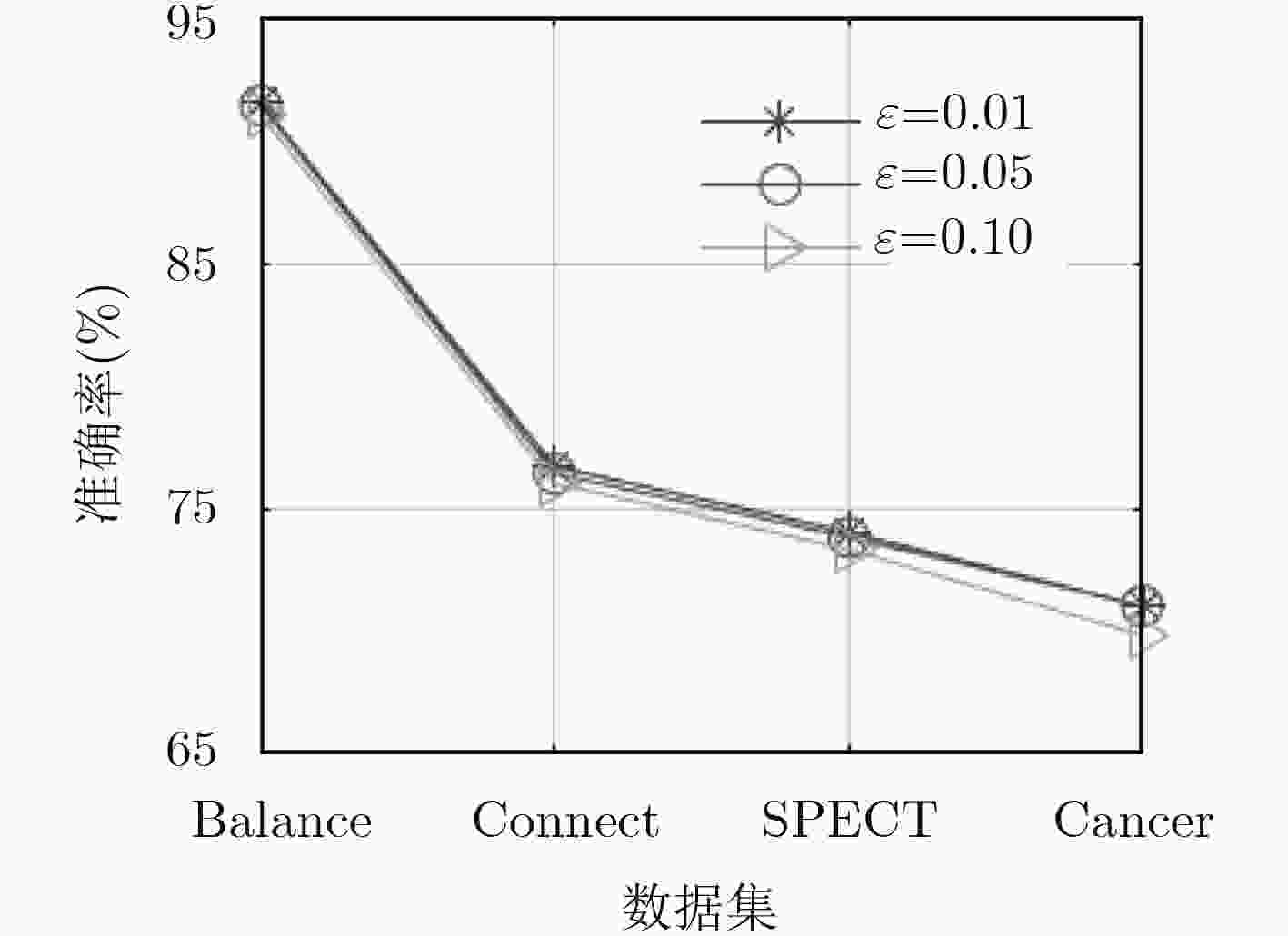
$\varepsilon $ 信息数据集 阈值$\varepsilon $ 平均准确率 Balance 0.01/0.05/0.10 0.915/0.914/0.910 Connect 0.01/0.05/0.10 0.767/0.764/0.760 SPECT 0.01/0.05/0.10 0.740/0.738/0.733 Cancer 0.01/0.05/0.10 0.710/0.710/0.698 表 5 NB, TAN和SETAN的各项分类指标对比情况
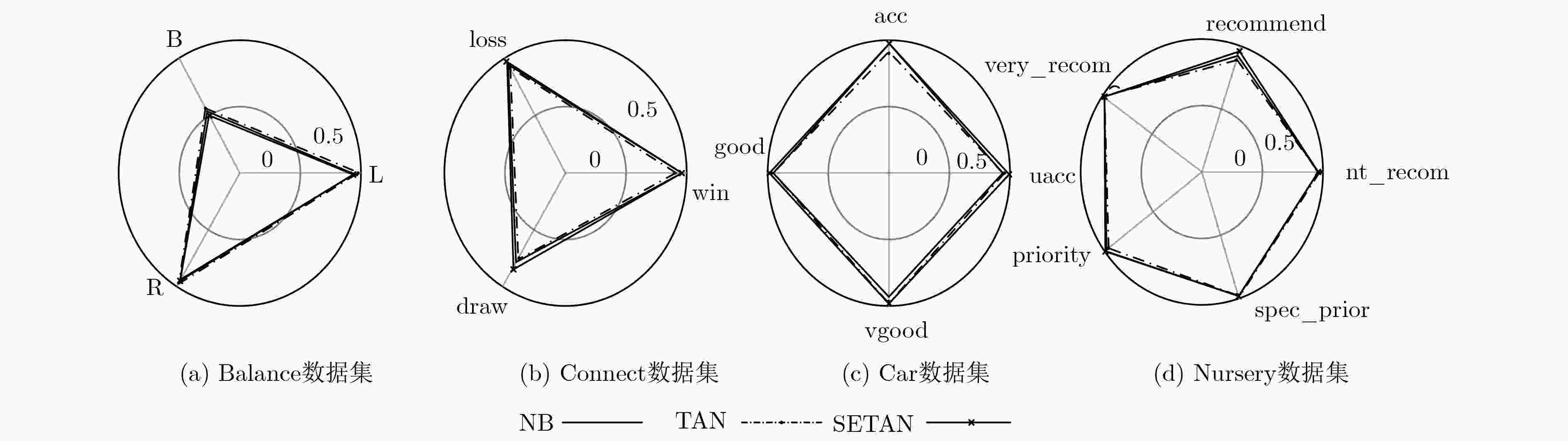
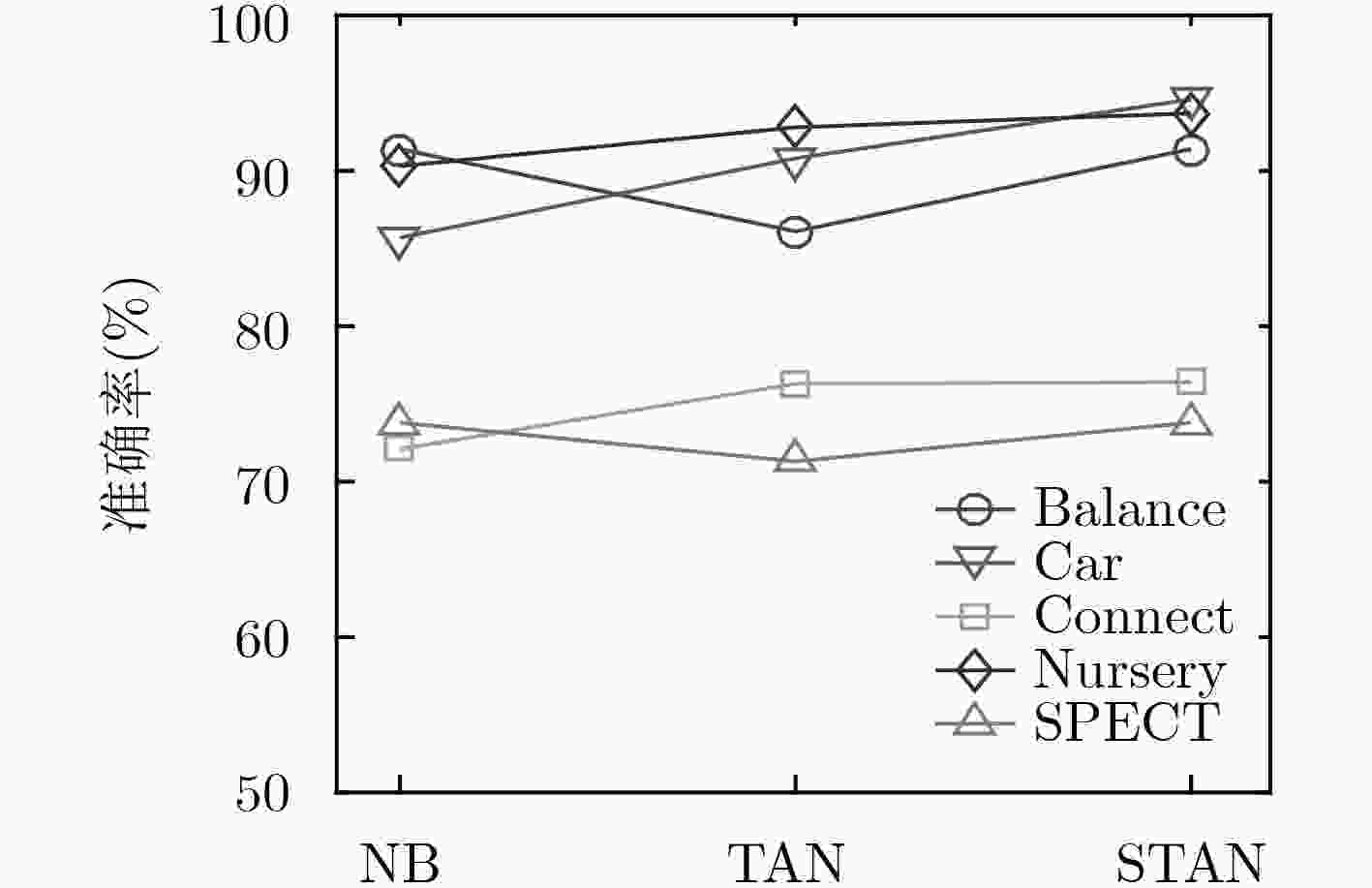
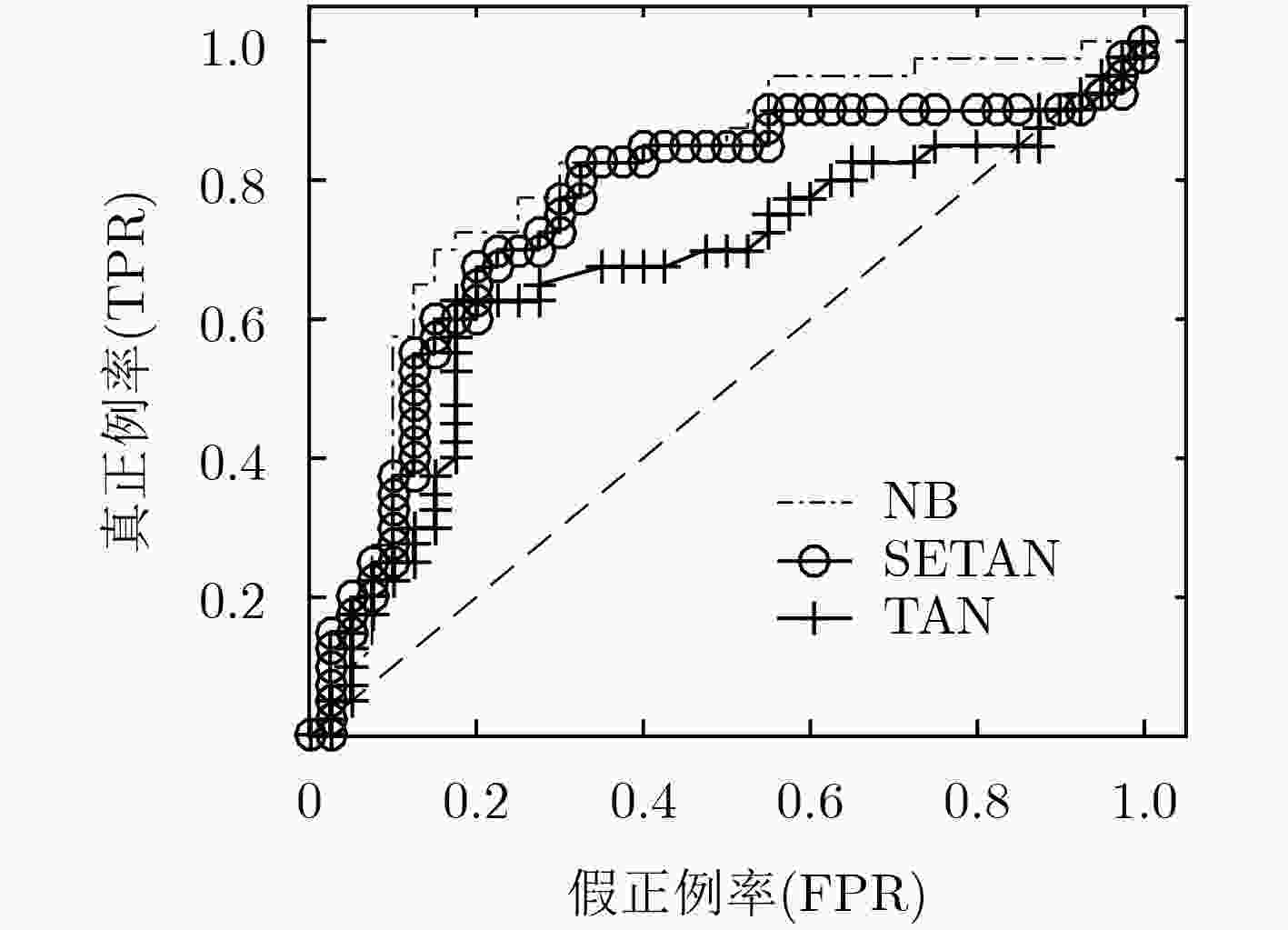
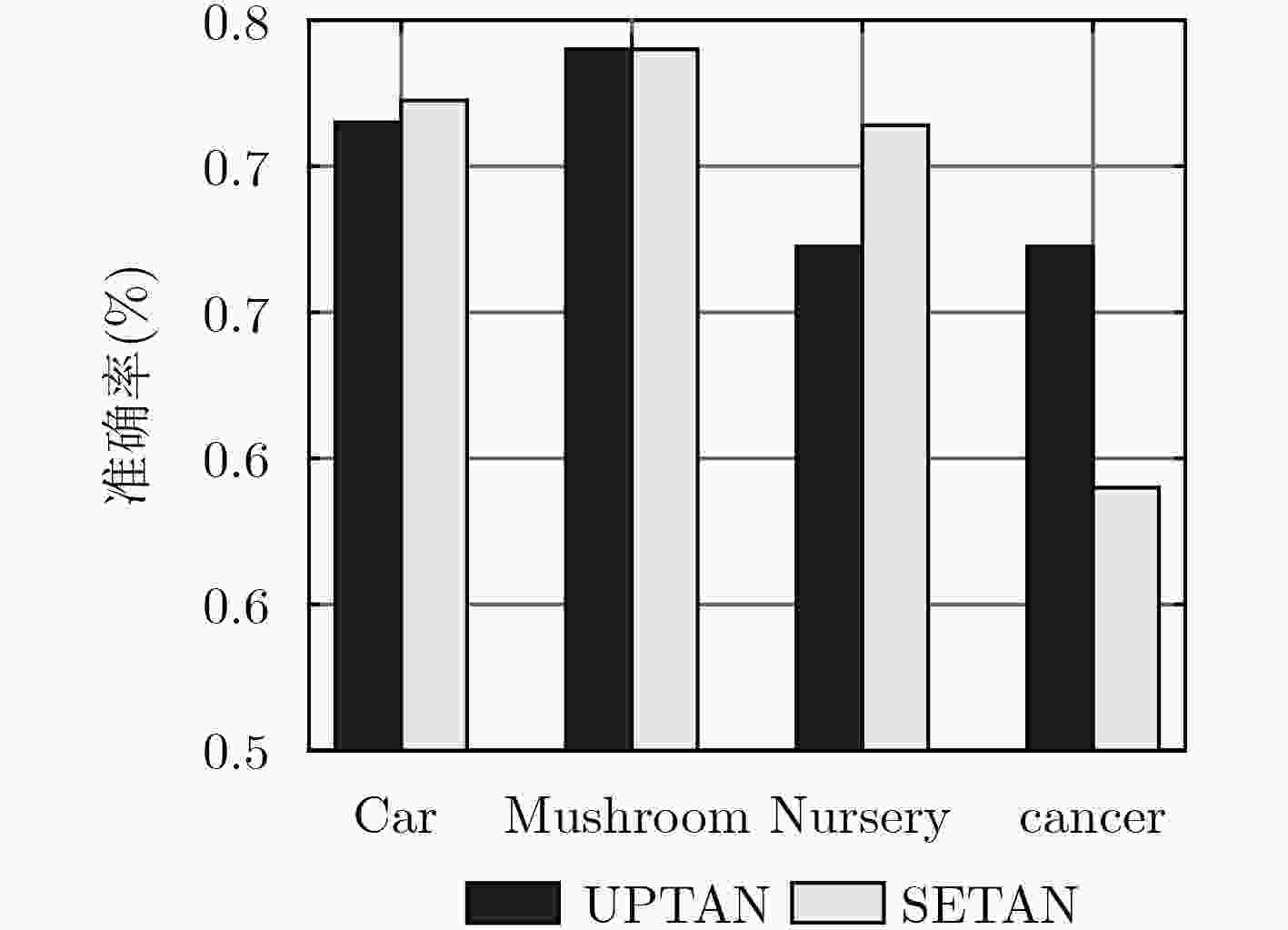
数据集 算法 准确率 F1值 召回率 精确率 AUC面积 NB 0.914 0.876 0.914 0.842 0.961 Balance TAN 0.861 0.834 0.861 0.836 0.904 SETAN 0.914 0.876 0.914 0.842 0.962 NB 0.857 0.849 0.857 0.854 0.976 Car TAN 0.908 0.911 0.908 0.92 0.983 SETAN 0.946 0.947 0.946 0.947 0.988 NB 0.721 0.681 0.721 0.681 0.807 Connect TAN 0.763 0.722 0.763 0.731 0.864 SETAN 0.764 0.724 0.764 0.735 0.866 NB 0.958 0.958 0.958 0.96 0.998 Mushroom TAN 0.999 1.000 0.999 1.000 1.000 SETAN 1.000 1.000 1.000 1.000 1.000 NB 0.903 0.894 0.903 0.906 0.982 Nursery TAN 0.928 0.92 0.928 0.929 0.991 SETAN 0.937 0.927 0.937 0.937 0.993 NB 0.738 0.735 0.738 0.745 0.802 SPECT TAN 0.713 0.709 0.713 0.724 0.668 SETAN 0.738 0.736 0.738 0.741 0.755 NB 0.734 0.727 0.734 0.723 0.702 Cancer TAN 0.706 0.692 0.706 0.687 0.667 SETAN 0.710 0.700 0.710 0.695 0.624 NB 0.901 0.902 0.901 0.905 0.973 Votes TAN 0.940 0.940 0.940 0.941 0.986 SETAN 0.949 0.950 0.949 0.950 0.985 -
PEARL J. Probabilistic reasoning in intelligent systems: networks of plausible inference[J]. Computer Science Artificial Intelligence, 1991, 70(2): 1022–1027. doi: 10.2307/407557 WEBB G I, CHEN Shenglei, and N A. Zaidi Scalable learning of Bayesian network classifiers[J]. Journal of Machine Learning Research, 2016, 17(1): 1515–1549. MURALIDHARAN V and SUGUMARAN V. A comparative study of Naïve Bayes classifier and Bayes net classifier for fault diagnosis of monoblock centrifugal pump using wavelet analysis[J]. Applied Soft Computing, 2012, 12(8): 2023–2029. doi: 10.1016/j.asoc.2012.03.021 Friedman N, Geiger D, and Goldszmidt M. Bayesian network classifiers[J]. Machine Learning, 1997, 29(2-3): 131–163. doi: 10.1023/a:1007465528199 GAN Hongxiao, ZHANG Yang, and SONG Qun. Bayesian belief network for positive unlabeled learning with uncertainty[J]. Pattern Recognition Letters, 2017, 90. doi: 10.1016/j.patrec.2017.03.007 JIANG Liangxiao, CAI Zhihua, WANG Dianhong, et al. Improving Tree augmented Naive Bayes for class probability estimation[J]. Knowledge-Based Systems, 2012, 26: 239–245. doi: 10.1016/j.knosys.2011.08.010 王中锋, 王志海. TAN分类器结构等价类空间及其在分类器学习算法中的应用[J]. 北京邮电大学学报, 2012, 35(1): 72–76. doi: 10.3969/j.issn.1007-5321.2012.01.017WANG Zhongfeng and WANG Zhihai. Equivalent classes of TAN classifier structure and their application on learning algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(1): 72–76. doi: 10.3969/j.issn.1007-5321.2012.01.017 DUAN Zhiyi and WANG Limin. K-dependence bayesian classifier ensemble[J]. Entropy, 2017, 19(12): 651. doi: 10.3390/e19120651 冯月进, 张凤斌. 最大相关最小冗余限定性贝叶斯网络分类器学习算法[J]. 重庆大学学报, 2014, 37(6): 71–77. doi: 10.11835/j.issn.1000-582X.2014.06.011FENG Yuejin and ZHANG Fengbi. Max-relevance min-redundancy restrictive BAN classifier learning algorithm[J]. Journal of Chongqing University:Natural Science, 2014, 37(6): 71–77. doi: 10.11835/j.issn.1000-582X.2014.06.011 WONG M L and LEUNG K S. An efficient data mining method for learning bayesian networks using an evolutionary algorithm-based hybrid approach[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(4): 378–404. doi: 10.1109/TEVC.2004.830334 LOU Hua, WANG Limin, DUAN Dingbo, et al. RDE: A novel approach to improve the classification performance and expressivity of KDB[J]. Plos One, 2018, 13(7): e0199822. doi: 10.1371/journal.pone.0199822 ROBINSON R W. Counting Unlabeled Acyclic Digraphs[M]. Berlin Heidelberg: Springer, 1977: 28–43. doi: 10.1007/BFb0069178. SCHWARZ G. Estimating the Dimension of a Model[J]. Annals of Statistics, 1978, 6(2): 15–18. GREINER R and ZHOU W. Structural extension to logistic regression: discriminative parameter learning of belief net classifiers[J]. Machine Learning, 2005, 59(3): 297–322. doi: 10.1007/s10994-005-0469-0 MADDEN M G. On the classification performance of TAN and general bayesian networks[J]. Knowledge-Based Systems, 2009, 22(7): 489–495. doi: 10.1016/j.knosys.2008.10.006 DRUGAN M M and WIERING M A. Feature selection for Bayesian network classifiers using the MDL-FS score[J]. International Journal of Approximate Reasoning, 2010, 51(6): 695–717. doi: 10.1016/j.ijar.2010.02.001 WU Jiehua. A generalized tree augmented naive bayes link prediction model[J]. Journal of Computational Science, 2018. doi: 10.1016/j.jocs.2018.04.006 MEHRJOU A, HOSSEINI R, and ARAABI B N. Improved Bayesian information criterion for mixture model selection[J]. Pattern Recognition Letters, 2016, 69: 22–27. doi: 10.1016/j.patrec.2015.10.004 杜瑞杰. 贝叶斯分类器及其应用研究[D]. [硕士论文], 上海大学, 2012.DU Ruijie. The Research of Bayesian Classifier and its applications[D]. [Master disertation], Shanghai University, 2012 -





 下载:
下载:




 下载:
下载:
