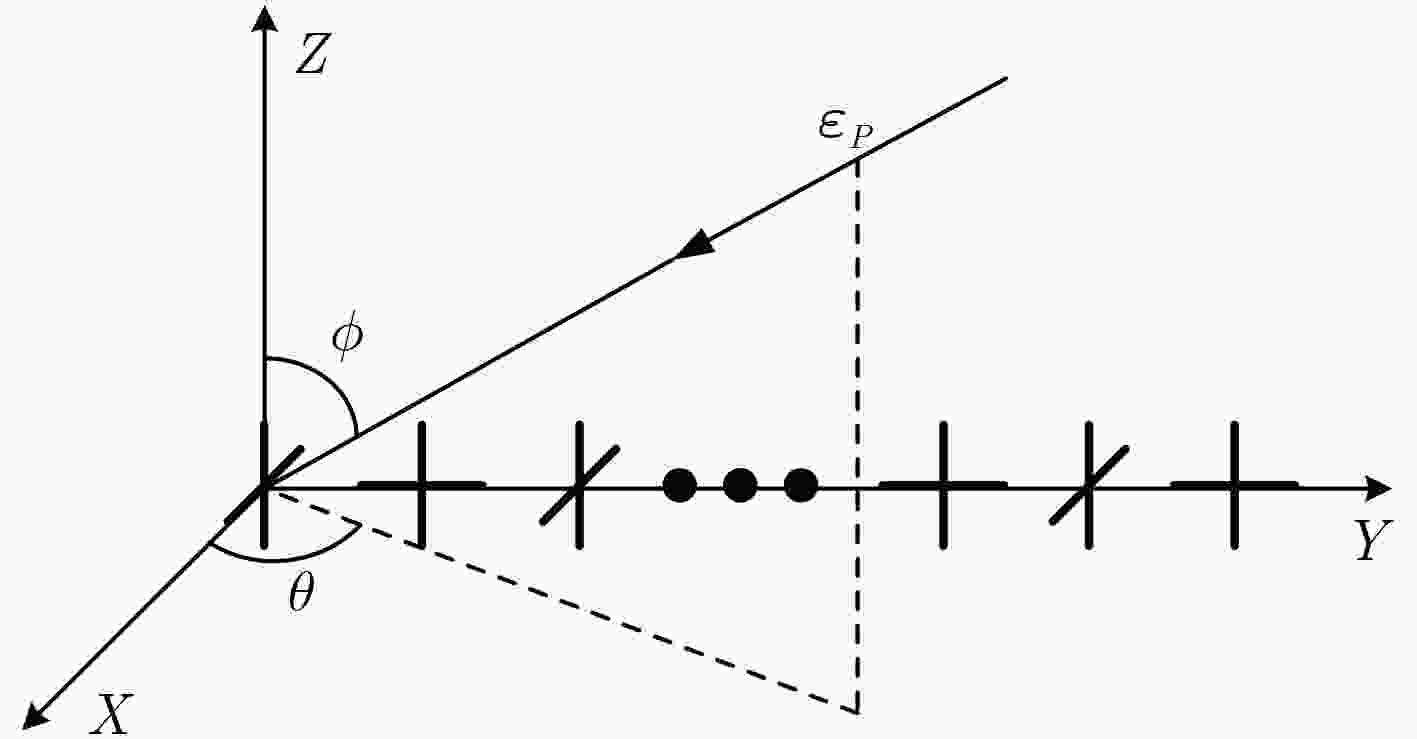
Two Dimensional DOA Estimation Based on Polarization Sensitive Array and Uniform Linear Array
-
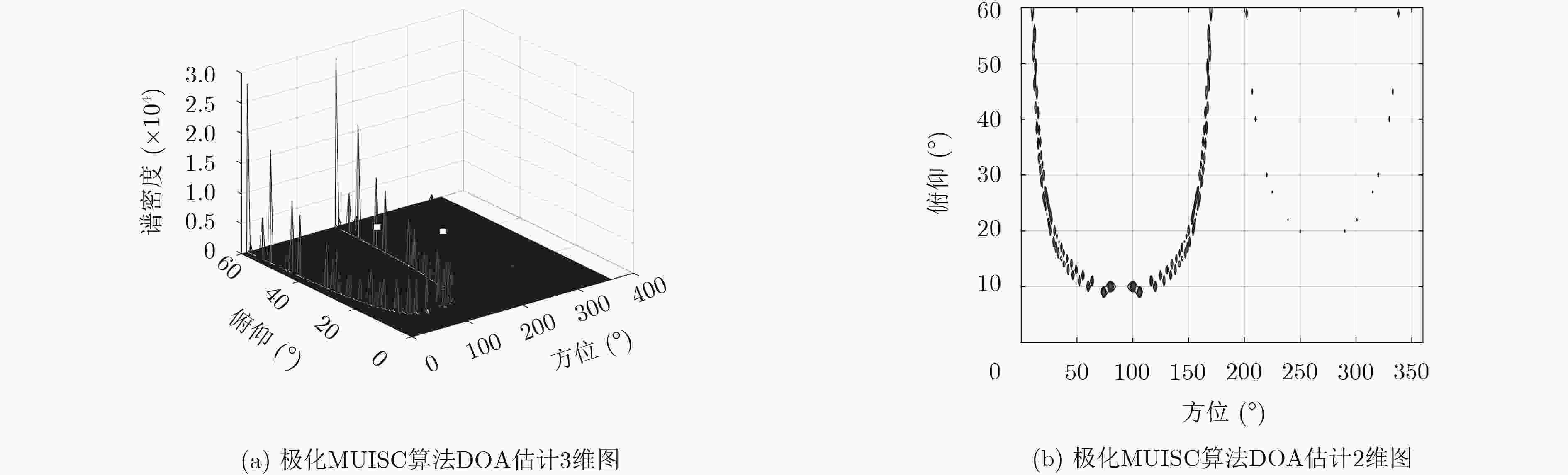
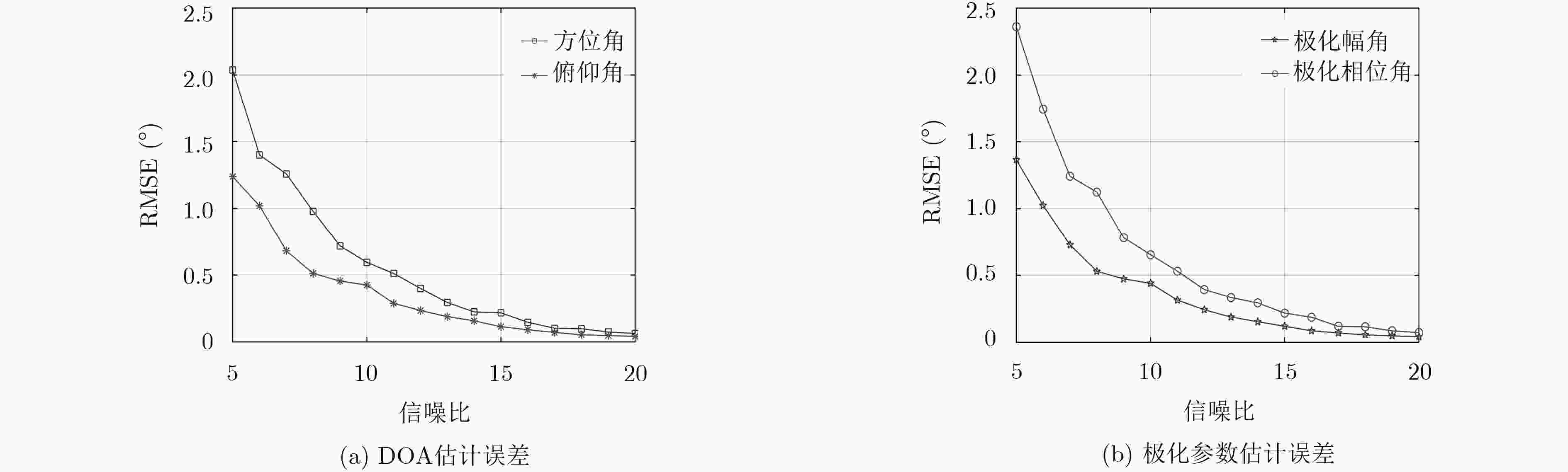
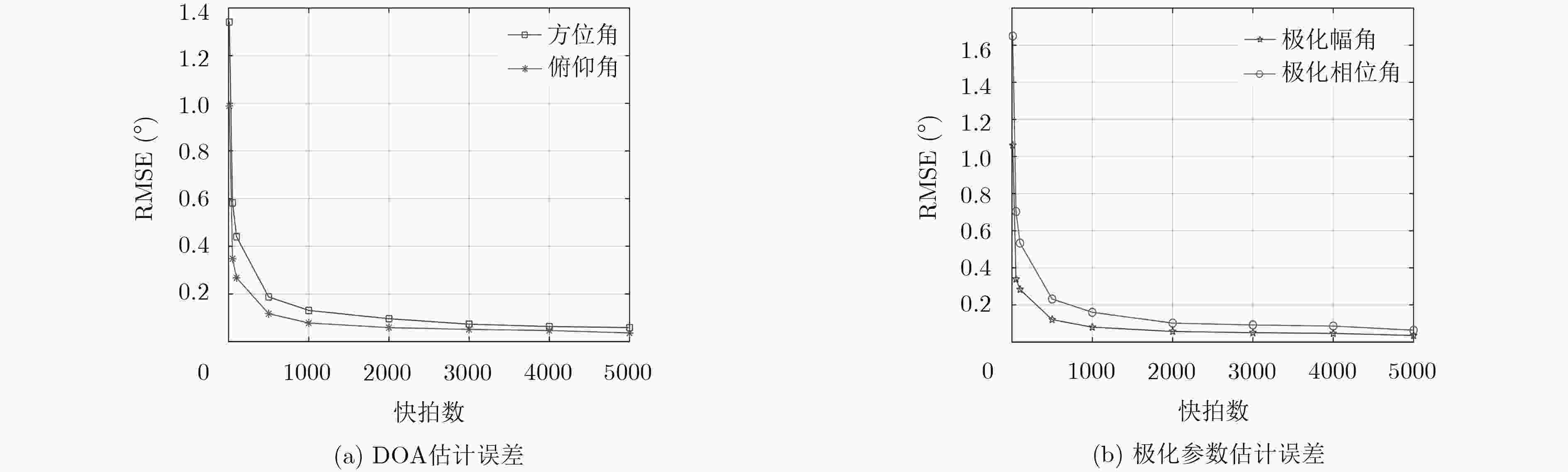
摘要: 针对残缺电磁矢量传感器的极化敏感阵列多参数联合估计问题,该文提出一种基于正交偶极子的均匀线阵的2维波达方向(Direction-Of-Arrival, DOA)估计算法。首先,对极化敏感阵列的接收数据矢量的协方差矩阵进行特征分解,然后将信号子空间划分成4个子阵,根据旋转不变子空间(ESPRIT)算法分别求出其中1个子阵与其它3个子阵的相位差,再对不同子阵间的相位差进行配对,最后根据相位差求出信号的DOA估计和极化参数。由正交偶极子组成的均匀线阵使用极化MUSIC算法和传统ESPRIT算法无法进行2维DOA估计,该文提出的算法解决了这个问题,并且相较于极化MUISC算法降低了算法的复杂度。仿真结果验证了该文算法的有效性。Abstract: To solve the problem that polarization sensitive array of defective electromagnetic vector sensor estimate multi parameter, a two-dimensional DOA estimation algorithm based on orthogonal dipole is proposed in this paper. First, eigendecomposition of the covariance matrix is produced by the received data vectors of the polarization sensitive array. Then the signal subspace is divided into four subarrays, and the phase difference between one of the subarray and the others is obtained according to the ESPRIT algorithm. Then the phase difference between different subarrays is paired. Finally, the DOA estimation and polarization parameters of the signal are calculated according to the phase difference. The uniform linear array composed by orthogonal dipoles can not be two-dimensional DOA estimated by using the MUSIC algorithm and the traditional ESPRIT algorithm. The algorithm proposed in this paper solves this problem, and compared with the polarization MUISC algorithm greatly reduces the complexity of the algorithm. The simulation results verify the effectiveness of the proposed algorithm.
-
表 1 方位角的判别方法
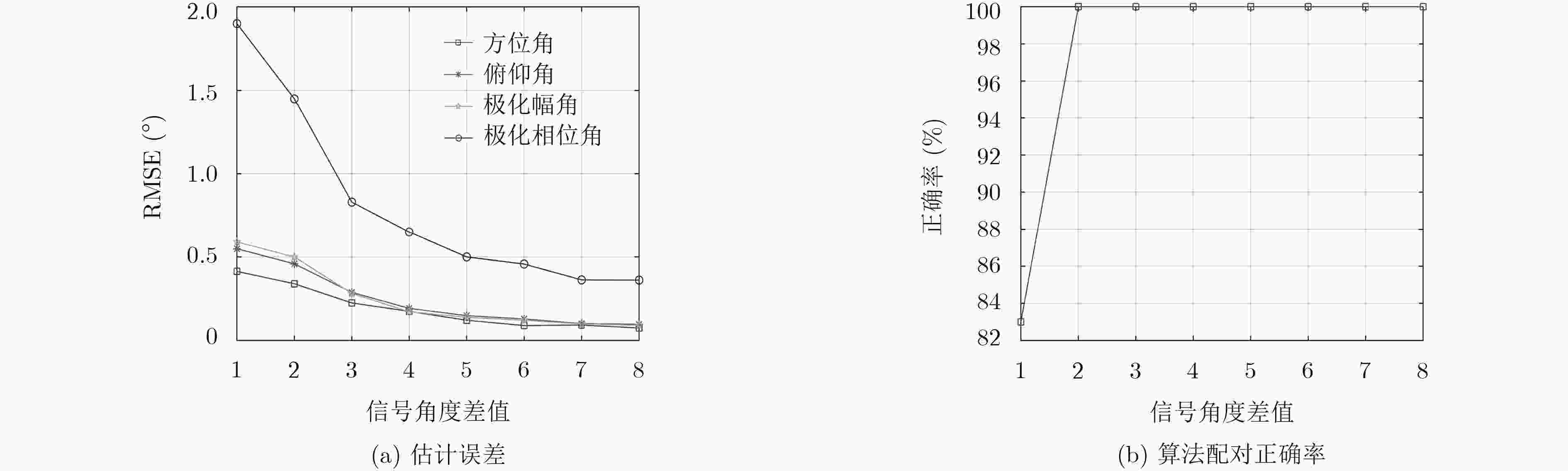
$\sin \theta \sin \phi > 0$ $\sin \theta \sin \phi < 0$ $\tan \theta > 0$ 第1象限 第3象限 $\tan \theta < 0$ 第2象限 第4象限 表 2 本文算法的仿真结果(°)
方位角 俯仰角 极化幅角 极化相位角 实际值 估计值 实际值 估计值 实际值 估计值 实际值 估计值 信号1 60.00 60.17 10.00 9.92 10.00 10.06 130.00 130.10 信号2 150.00 150.00 20.00 20.13 20.00 19.83 60.00 59.68 信号3 220.00 220.00 30.00 29.99 30.00 30.01 300.00 300.00 -
陈善继, 张锐戈, 吴国庆, 等. 极化敏感阵列及其应用研究[J]. 现代电子技术, 2009, 32(5): 53–56. doi: 10.16652/j.issn.1004-373x.2009.05.008CHEN Shanji, ZHANG Ruige, WU Guoqing, et al. Research on the polarization sensitive array and its application[J]. Modern Electronics Technique, 2009, 32(5): 53–56. doi: 10.16652/j.issn.1004-373x.2009.05.008 NEHORAI A and PALDI E. Vector-sensor array processing for electromagnetic source localization[J]. IEEE Transactions on Signal Processing, 1994, 42(2): 376–398. doi: 10.1109/78.275610 FERRARA E R Jr and PARKS T M. Direction finding with an array of antennas having diverse polarizations[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(2): 231–236. doi: 10.1109/TAP.1983.1143038 HUA Y. A pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(3): 370–376. doi: 10.1109/8.233122 CHENG Qi and HUA Yingbo. Performance analysis of the MUSIC and Pencil-MUSIC algorithms for diversely polarized array[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3150–3165. doi: 10.1109/78.330374 CHENG Qi and HUA Yingbo. Further study of the Pencil-MUSIC algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 284–299. doi: 10.1109/7.481269 GUO Ran, MAO Xingpeng, LI Shaobin, et al. A fast DOA estimation algorithm based on polarization MUSIC[J]. Radioengineering, 2015, 24(1): 214–225. doi: 10.13164/re.2015.0214 FRIEDLANDER B and WEISS A J. A direction finding algorithm for diversely polarized arrays[J]. Digital Signal Processing, 1992, 2(3): 123–134. doi: 10.1016/1051-2004(92)90002-G WEISS A J and FRIEDLANDER B. Direction finding for diversely polarized signals using polynomial rooting[J]. IEEE Transactions on Signal Processing, 1993, 41(5): 1893–1905. doi: 10.1109/78.215307 LI Jian and COMPTON R T Jr. Angle and polarization estimation using ESPRIT with a polarization sensitive array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(9): 1376–1383. doi: 10.1109/8.99047 LI Jian and COMPTON R T Jr. Angle estimation using a polarization sensitive array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(10): 1539–1543. doi: 10.1109/8.97389 LI Jian and COMPTON R T Jr. Two-dimensional angle and polarization estimation using the ESPRIT algorithm[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(5): 550–555. doi: 10.1109/8.142630 LIU Shuai, YAN Fenggang, JIN Ming, et al. An improved polarization and DOA estimation algorithm[C]. 2016 IEEE International Conference on Microwave and Millimeter Wave Technology, Beijing, China, 2016: 1009–1011. WANG Guibao, ZHAO Feng, and LIU Xiang. Estimating the DOA and polarization parameters with sparse collocated loop and dipole cross array[C]. 2016 IEEE International Conference on Real-time Computing and Robotics, Angkor Wat, Cambodia, 2016: 306–311. LAN Xiang, LIU Wei, and NGAN H Y T. Joint 4-D DOA and polarization estimation based on linear tripole arrays[C]. The 22nd International Conference on Digital Signal Processing, London, UK, 2017: 1–5. 王利伟, 朱晓丹, 王建, 等. 基于极化敏感阵列的高效DOA与极化参数联合估计算法[J]. 航天电子对抗, 2017, 33(3): 42–46. doi: 10.16328/j.htdz8511.2017.03.012WANG Liwei, ZHU Xiaodan, WANG Jian, et al. Efficient DOA and polarization parameter joint estimation method based on polarization sensitive array[J]. Aerospace Electronic Warfare, 2017, 33(3): 42–46. doi: 10.16328/j.htdz8511.2017.03.012 -





 下载:
下载:


 下载:
下载:
