Controlled Physical Unclonable Function Research Based on Sensitivity Confusion Mechanism
-
摘要: 为了克服物理不可克隆函数(PUF)面对建模攻击的脆弱性,该文提出一种基于敏感度混淆机制的控制型PUF架构。根据PUF的布尔函数定义及Walsh谱理论,推导出各个激励位具有不同敏感度,分析并归纳了与混淆值位宽奇偶性有关的位置选取规则。利用该规则指导了多位宽混淆算法(MWCA)的设计,构建了具有高安全性的控制型PUF架构。将基础PUF结构作为控制型PUF的防护对象进行实验评估,发现基于敏感度混淆机制的控制型PUF所产生的响应具有较好的随机性。采用逻辑回归算法对不同PUF结构进行建模攻击,实验结果表明,相比基本ROPUF、仲裁器PUF以及基于随机混淆机制的OB-PUF,基于敏感度混淆机制的控制型PUF能够显著提高PUF的抗建模攻击能力。Abstract: In order to overcome the vulnerability of Physical Unclonable Function (PUF) to modeling attacks, a controlled PUF architecture based on sensitivity confusion mechanism is proposed. According to the Boolean function definition of PUF and Walsh spectrum theory, it is derived that each excitation bit has different sensitivity, and the position selection rules related to the parity of the confound value bit width are analyzed and summarized. This rule guides the design of the Multi-bit Wide Confusion Algorithm (MWCA) and constructs a controlled PUF architecture with high security. The basic PUF structure is evaluated as a protective object of the controlled PUF. It is found that the response generated by the controlled PUF based on the sensitivity confusion mechanism has better randomness. Logistic regression algorithm is used to model different PUF attack. The experimental results show that compared with the basic ROPUF, the arbiter PUF and the OB-PUF based on the random confusion mechanism, the controlled PUF based on the sensitivity confusion mechanism can significantly improve the PUF resistance capabilities for modeling attack.
-
Key words:
- Information security /
- Machine learning /
- Boolean function /
- Sensitivity information
-
表 1
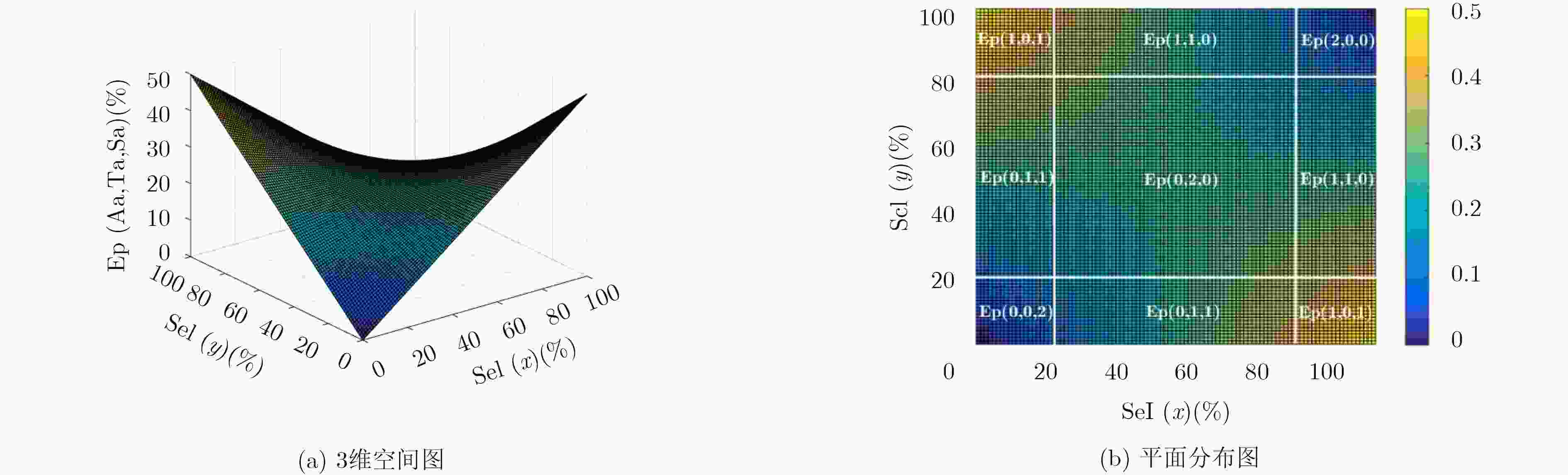
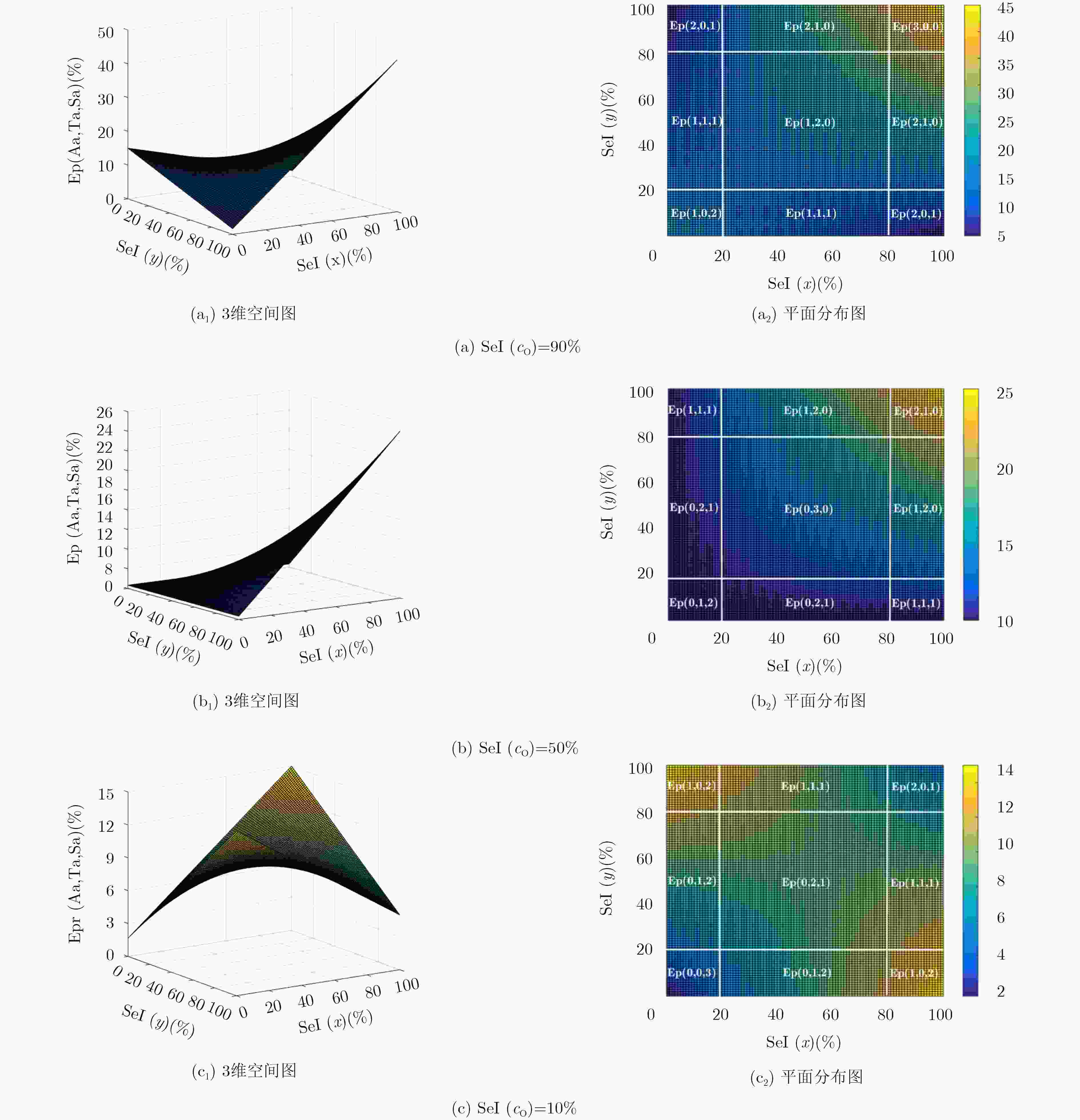
${N_{{\rm{OB}}}} = {\rm{1}},2,{\rm{3}},{\rm{4}}$ 时混淆值位置选择所有组合情况NOB (Aa,Ta,Sa) 1 (1,0,0);(0,1,0);(0,0,1) 2 (1,1,0);(1,0,1);(0,1,1);(2,0,0);(0,2,0);(0,0,2) 3 (1,1,1);(2,1,0);(2,0,1);(1,2,0);(0,2,1);(1,0,2);(0,1,2);
(3,0,0);(0,3,0);(0,0,3)4 (2,1,1);(1,2,1);(1,1,2);(2,2,0);(2,0,2);(0,2,2);(3,1,0);(3,0,1);
(1,3,0);(0,3,1);(1,0,3);(0,1,3);(4,0,0);(0,4,0);(0,0,4)表 2 MWCA的具体算法
输入:混淆激励集合${C_{\rm OB}} = \left\{ {c_{\rm OB}^k|k \in \left\{ {1,2, ·\!·\!· ,\sum\nolimits_{i = 1}^t {{2^{N - i}}} } \right\}} \right\}; $ 混淆值集合$Y = \left\{ {{y_k}|k \in \left\{ {1,2, ·\!·\!· ,\sum\nolimits_{i = 1}^t {{2^{N - i}}} } \right\}} \right\} $ 过程: $(1)\;{\rm for}\;\forall k \in \left\{ {1,2, ·\!·\!· ,\sum\nolimits_{i = 1}^t {{2^{N - i}}} } \right\}{\rm do} $ $(2)\;{\text{输入混淆激励集合}}c_{\rm OB}^k = \left\{ {{c_1},{c_2}, ·\!·\!· ,{c_t}} \right\}\text{、}\ {\text{混淆值}}{y_k}{\text{和标识值}}{a_k} ; $ $(3)\;{\rm if}\;{a_k} = 1\;{\rm then} $ $(4)\;{\text{调用位置选择策略}}{P_k} ;{\text{产生完整激励}}{C_k}{\rm{ = }}{P_k}(c_{{\rm{OB}}}^k,{y_k}) ;{\rm return} $ $(5)\;{\rm else} $ $(6)\;{\text{计算}}{{ r = ({N} - t) }}\% 2 ; $ $(7)\;\rm end\;if$ $(8)\;{\rm if}\;r = 0\;{\rm then}$ $(9)\;{\text{调用偶数规则}}{\rm{Rule}}\_{\rm E},{\text{生成位置选择策略}}{P_k},{a_k} = 1;$ $(10)\;\rm else $ $(11)\;{\text{调用奇数规则}}{\rm{Rule}}\_{\rm O},{\text{生成位置选择策略}}{P_k},{a_k} = 1;$ $(12)\;\rm end\;if $ $(13)\;{\text{存储标识值}}{a_k}{\text{和策略}}{P_k} ,{\text{用于之后激励混淆步骤的判断依据}} ;$ (14) 按照策略将混淆值插入混淆激励$c_{{\rm{OB}}}^k,$产生完整激励 ${C_k}{\rm{ = }}{P_k}(c_{{\rm{OB}}}^k,{y_k}) ;\rm return$ $ (15) \;\rm end\;for$ 输出:完整激励集合${C_f} = {\rm{\{ }}{C_k}|k \in {\rm{\{ }}1,2, ·\!·\!· ,\sum\nolimits_{i = 1}^t {{2^{N - i}}} {\rm{\} \} }}。$ 表 3 可靠性和唯一性指标对比结果
表 4 NIST随机数测试结果
测试项目 基本ROPUF[10] 本文 P_value 结果 P_value 结果 频率检验 0.000003 失败 0.829896 通过 块内频数检验 0.050764 通过 0.580358 通过 向前累加和检验 0.000000 失败 0.502594 通过 向后累加和检验 0.000000 失败 0.347179 通过 游程检验 0.302788 通过 0.329404 通过 块内最长游程检验 0.000062 失败 0.024892 通过 近似熵检验 0.000001 失败 0.693147 通过 向前序列检验 0.070160 通过 0.024892 通过 向后序列检验 0.192277 通过 0.756264 通过 表 5 不同PUF结构的攻击结果对比
PUF类型 训练集数量 攻击时间(s) 预测成功率(%) OB-PUF(1) 4400 26 87.6 OB-PUF(2) 5200 30 84.4 OB-PUF(3) 6000 62 73.1 OB-PUF(4) 8000 128 69.8 基本ROPUF 5200 8 99.5 控制型ROPUF 7200 262 53.4 仲裁器PUF 4800 15 93.9 控制型APUF 6500 187 67.2 -
RÜHRMAIR U, SÖLTER J, SEHNKE F, et al. PUF modeling attacks on simulated and silicon data[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(11): 1876–1891. doi: 10.1109/TIFS.2013.2279798 GASSEND B, VAN DIJK M, CLARKE D, et al. Controlled physical random functions[J]. ACM Transactions on Information and System Security, 2008, 10(4): 23–25. KATZENBEISSER S, KOÇABAS Ü, VAN DER LEEST V, et al. Recyclable PUFs: Logically Reconfigurable PUFs[M]. Berlin, Germamy: Springer, 2011: 374–389. LAO Yingjie and PARHI K K. Reconfigurable architectures for silicon physical unclonable functions[C]. Proceedings of 2011 IEEE International Conference on Electro/Information Technology, Mankato, USA, 2011: 1–7. MAJZOOBI M, KOUSHANFAR F, and POTKONJAK M. Techniques for design and implementation of secure reconfigurable PUFs[J]. ACM Transactions on Reconfigurable Technology and Systems, 2009, 2(1): 5. GAO Yansong, AL-SARAWI S F, ABBOTT D, et al. Modeling attack resilient reconfigurable latent obfuscation technique for PUF based lightweight authentication[J]. arXiv:1706.06232, 2017. 许道云, 韦立, 王晓峰. 布尔函数的学习与性质测试[J]. 武汉大学学报: 理学版, 2012, 58(2): 125–134.XU Daoyun, WEI Li, and WANG Xiaofeng. Learning and testing of properties for Boolean functions[J]. Journal of Wuhan University:Natural Science Edition, 2012, 58(2): 125–134. GANJI F, TAJIK S, FÄßLER F, et al. Strong machine learning attack against PUFs with no mathematical model[C]. Proceedings of the 18th International Conference on Cryptographic Hardware and Embedded Systems, Santa, USA, 2016: 391–411. ZALIVAKA S S, PUCHKOV A V, KLYBIK V P, et al. Multi-valued arbiters for quality enhancement of PUF responses on FPGA implementation[C]. Proceedings of 201621st Asia and South Pacific Design Automation Conference, Macau, China, 2016: 533–538. GASSEND B, CLARKE D, VAN DIJK M, et al. Silicon physical random functions[C]. Proceedings of the 9th ACM Conference on Computer and Communications Security, USA, 2002: 148–160. LAO Yingjie and PARHI K K. Statistical analysis of MUX-based physical unclonable functions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2014, 33(5): 649–662. doi: 10.1109/TCAD.2013.2296525 庞子涵, 周强, 高文超, 等. FPGA物理不可克隆函数及其实现技术[J]. 计算机辅助设计与图形学学报, 2017, 29(9): 1590–1603. doi: 10.3969/j.issn.1003-9775.2017.09.002PANG Zihan, ZHOU Qiang, GAO Wenchao, et al. Hardware implementation of physical unclonable function on FPGAs[J]. Journal of Computer-Aided Design &Computer Graphics, 2017, 29(9): 1590–1603. doi: 10.3969/j.issn.1003-9775.2017.09.002 DENG R, WENG Jian, REN Kui, et al. Security and Privacy in Communication Networks[M]. Cham: Springer, 2016: 675–693. KODÝTEK F and LÓRENCZ R. Proposal and properties of ring oscillator-based PUF on FPGA[J]. Journal of Circuits, Systems and Computers, 2016, 25(3): 1640016. doi: 10.1142/S0218126616400168 KODÝTEK F, LÓRENCZ R, and BUČEK J. Improved ring oscillator PUF on FPGA and its properties[J]. Microprocessors and Microsystems, 2016, 47: 55–63. doi: 10.1016/j.micpro.2016.02.005 -





 下载:
下载:







 下载:
下载:
