Homogenization Method for the Quadratic Polynomial Chaotic System
-
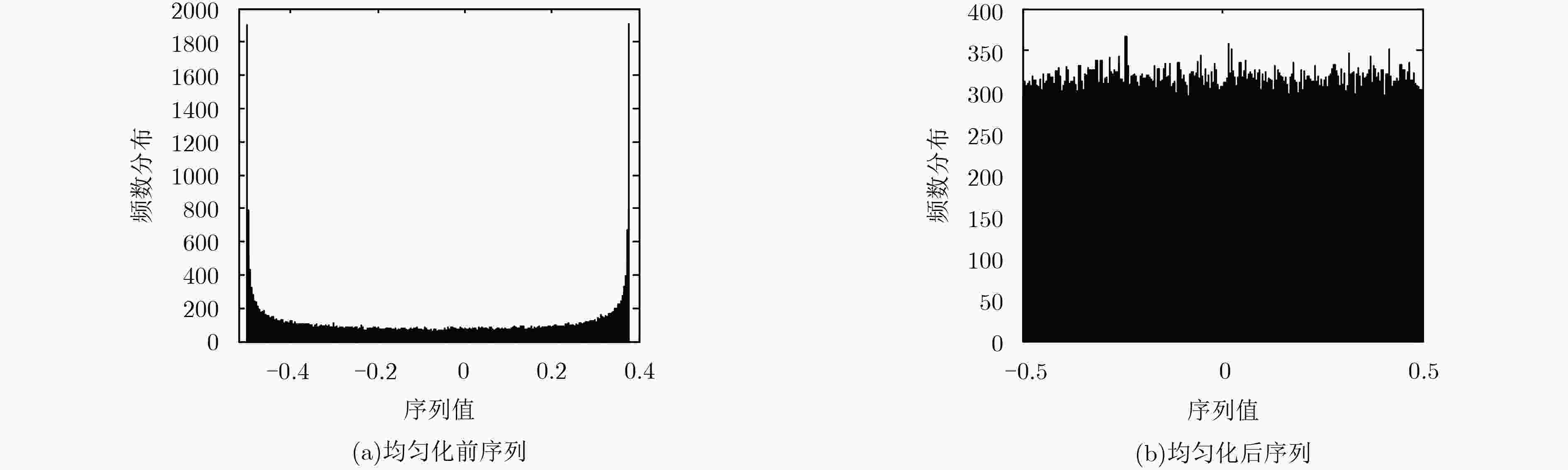
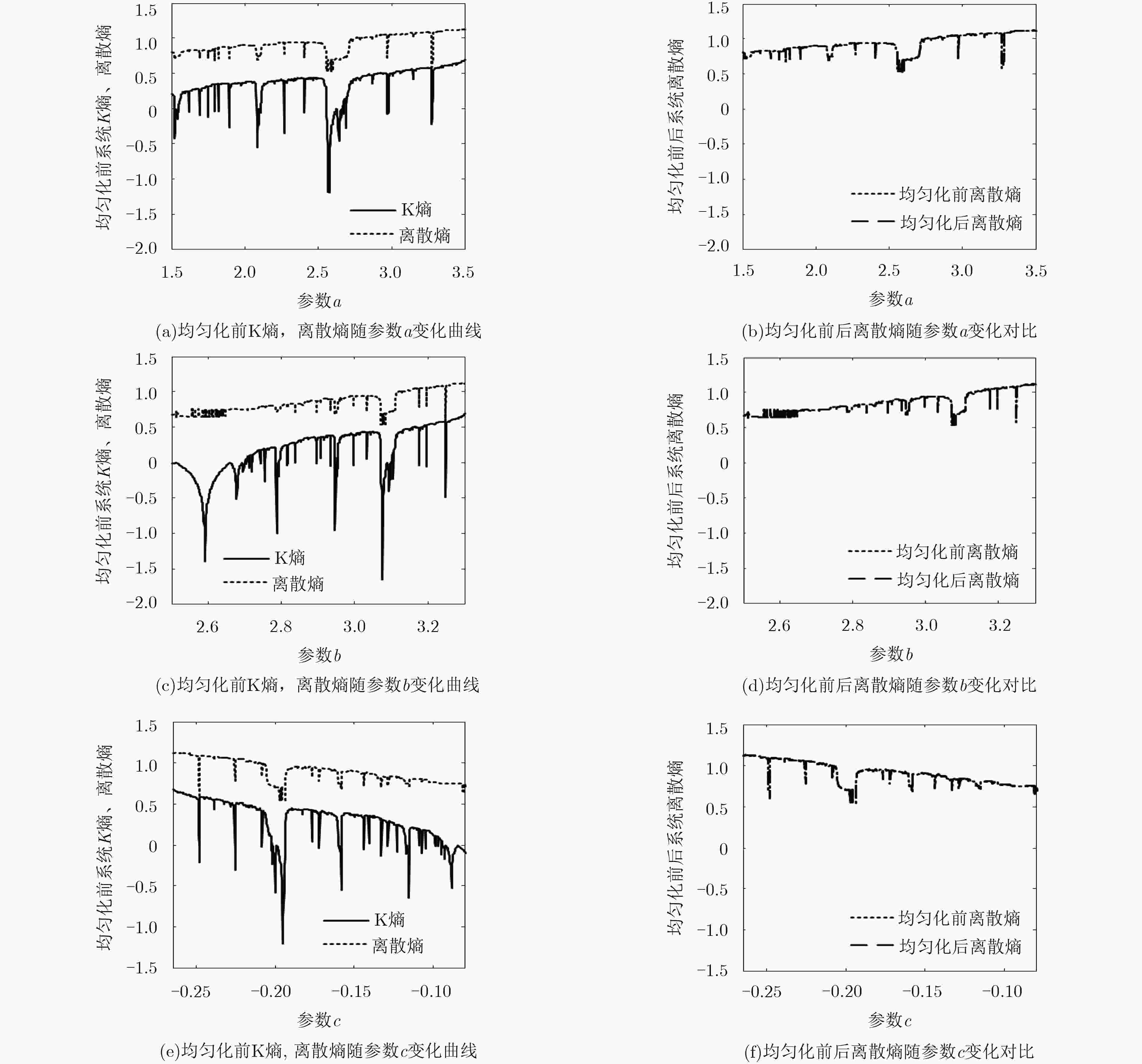
摘要: 该文给出了一般的2次多项式混沌系统与Tent映射拓扑共轭的充分条件,并依据该条件,给出了一类2次多项式混沌系统及其概率密度函数;进一步得到了能够将这类系统均匀化的变换函数;给出了一个新的2次多项式混沌系统并进行均匀化处理,对其产生的序列进行了信息熵、Kolmogorov熵和离散熵分析,结果显示该均匀化方法的均匀化效果显著且不改变序列混沌程度。Abstract: A sufficient condition for general quadratic polynomial systems to be topologically conjugate with Tent map is proposed. Base on this condition, the probability density function of a class of quadratic polynomial systems is provided and transformations function which can homogenize this class of chaotic systems is further obtained. The performances of both the original system and the homogenized system are evaluated. Numerical simulations show that the information entropy of the uniformly distributed sequences is closer to the theoretical limit and its discrete entropy remains unchanged. In conclusion, with such homogenization method all the chaotic characteristics of the original system is inherited and better uniformity is performed.
-
Key words:
- Chaotic system /
- Homogenization /
- Topologically conjugate /
- Entropy
-
表 1 几个2次多项式混沌系统
混沌系统$f(x)$ 概率密度 均匀化系统$z(x)$ $f(x)$信息熵 $z(x)$信息熵 $f(x) = \frac{7}{2}{x^2} + \frac{{33}}{{10}}x - \frac{{53}}{{200}}$ $\frac{7}{{{\text{π}} \sqrt { - 49{x^2} + 46.2x + 5.11} }}$ $z(x) = \frac{1}{{\text{π}} }\arcsin \left( { - \frac{7}{4}x - \frac{{33}}{{40}}} \right)$ 8.6470 8.9651 $f(x) = \frac{5}{4}{x^2} - \frac{1}{2}x - \frac{{27}}{{20}}$ $\frac{5}{{{\text{π}} \sqrt { - 25{x^2} + 10x + 63} }}$ $z(x) = \frac{1}{{\text{π}} }\arcsin\left( { - \frac{5}{8}x + \frac{1}{8}} \right)$ 8.6380 8.9649 $f(x) = - \frac{5}{2}{x^2} + 3x + \frac{1}{2}$ $\frac{5}{{{\text{π}} \sqrt { - 25{x^2} + 30x + 7} }}$ $z(x) = \frac{1}{{\text{π}} }\arcsin\left( {\frac{5}{4}x - \frac{3}{4}} \right)$ 8.6412 8.9650 表 2 系统均匀化前后的信息熵与最大熵比较
$\left( {N,M} \right)$ 均匀化前
信息熵均匀化后
信息熵最大熵 (500000, 100) 6.3530 6.6437 6.6439 (500000, 300) 7.9137 8.2284 8.2288 (500000, 500) 8.6431 8.9651 8.9658 -
LI T Y and YORKE J A. Period three implies chaos[J]. American Mathematical Monthly, 1975, 82(10): 985–992. doi: 10.1007/978-0-387-21830-4_6 MANFREDI P, VANDE GINSTE D, STIEVANO I S, et al. Stochastic transmission line analysis via polynomial chaos methods: an overview[J]. IEEE Electromagnetic Compatibility Magazine, 2017, 6(3): 77–84. doi: 10.1109/memc.0.8093844 KUMAR S, STRACHAN J P, and WILLIAMS R S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing[J]. Nature, 2017, 548(7667): 318–321. doi: 10.1038/nature23307 廖晓峰, 肖迪, 陈勇, 等. 混沌密码学原理及其应用[M]. 北京: 科学出版社, 2009: 16–40.LIAO Xiaofeng, XIAO Di, CHEN Yong, et al. Theory and Applications of Chaotic Cryptography[M]. Beijing: Science Press, 2009: 16–40. KOCAREV L and TASEV Z. Public-key encryption based on Chebyshev maps[C]. Proceedings of the 2003 International Symposium on Circuits and Systems, Bangkok, Thailand, 2003: 28–31. ROBINSON R C. An Introduction to Dynamical Systems: Continuous and Discrete[M]. Providence, Rhode Island: American Mathematical Society, 2012: 24–50. FRANK J and GOTTWALD G A. A note on statistical consistency of numerical integrators for multiscale dynamics[J]. Multiscale Modeling & Simulation, 2018, 16(2): 1017–1033. doi: 10.1137/17M1154709 黄诚, 易本顺. 基于抛物线映射的混沌LT编码算法[J]. 电子与信息学报, 2009, 31(10): 2527–2531.HUANG Cheng and YI Benshun. Chaotic LT encoding algorithm based on parabolic map[J]. Journal of Electronics &Information Technology, 2009, 31(10): 2527–2531. 曹光辉, 张兴, 贾旭. 基于混沌理论运行密钥长度可变的图像加密[J]. 计算机工程与应用, 2017, 53(13): 1–8. doi: 10.3778/j.issn.1002-8331.1703-0178CAO Guanghui, ZHANG Xing, and JIA Xu. Image encryption with variable-length running key based on chaotic theory[J]. Computer Engineering and Applications, 2017, 53(13): 1–8. doi: 10.3778/j.issn.1002-8331.1703-0178 KOCAREV L, SZCZEPANSKI J, AMIGO J M, et al. Discrete chaos-I: theory[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2006, 53(6): 1300–1309. doi: 10.1109/TCSI.2006.874181 AMIGÓ J M, KOCAREV L, and SZCZEPANSKI J. Theory and practice of chaotic cryptography[J]. Physics Letters A, 2007, 366(3): 211–216. doi: 10.1016/j.physleta.2007.02.021 AMIGÓ J M, KOCAREV L, and TOMOVSKI I. Discrete entropy[J]. Physica D: Nonlinear Phenomena, 2007, 228(1): 77–85. doi: 10.1016/j.physd.2007.03.001 臧鸿雁, 黄慧芳. 基于均匀化混沌系统生成S盒的算法研究[J]. 电子与信息学报, 2017, 39(3): 575–581. doi: 10.11999/JEIT160535ZANG Hongyan and HUANG Huifang. Research on algorithm of generating S-box based on uniform chaotic system[J]. Journal of Electronics &Information Technology, 2017, 39(3): 575–581. doi: 10.11999/JEIT160535 周海玲, 宋恩彬. 二次多项式映射的3-周期点判定[J]. 四川大学学报: 自然科学版, 2009, 46(3): 561–564.ZHOU Hailing and SONG Enbin. Discrimination of the 3-periodic points of a quadratic polynomial[J]. Journal of Sichuan University:Natural Science Edition, 2009, 46(3): 561–564. COLLET P and ECKMANN J P. Iterated Maps on the Interval as Dynamical Systems[M]. Boston: Birkhäuser, 2009. 郝柏林. 从抛物线谈起—混沌动力学引论[M]. 北京: 北京大学出版社, 2013: 114–118.HAO Bolin. Starting with Parabola: An Introduction to Chaotic Dynamics[M]. Beijing: Peking University Press, 2013: 114–118. -





 下载:
下载:


 下载:
下载:
