A Modified Adaptive Sea Clutter Suppression Algorithm Based on PSNR-HOSVD for Skywave OTHR
-
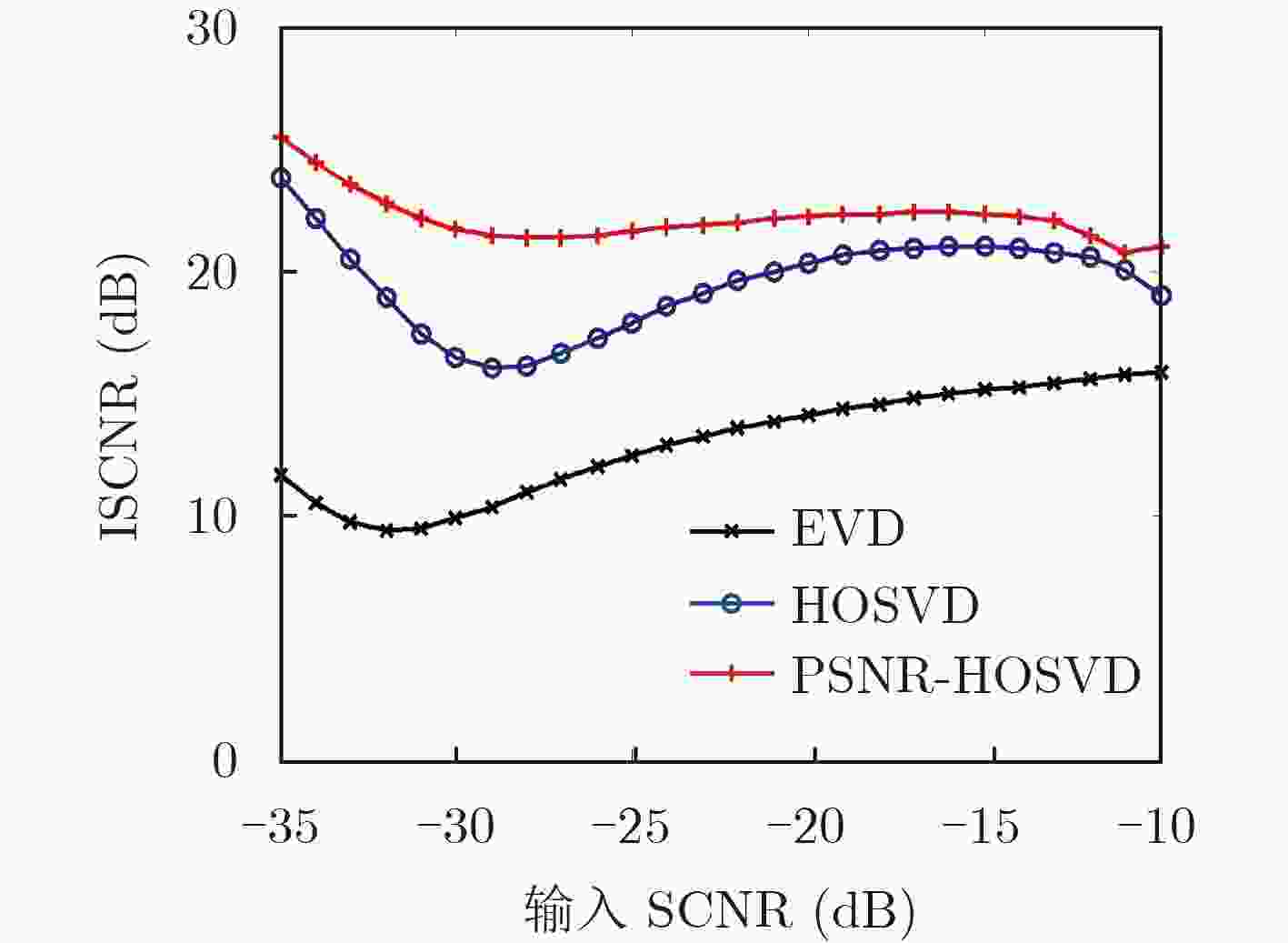
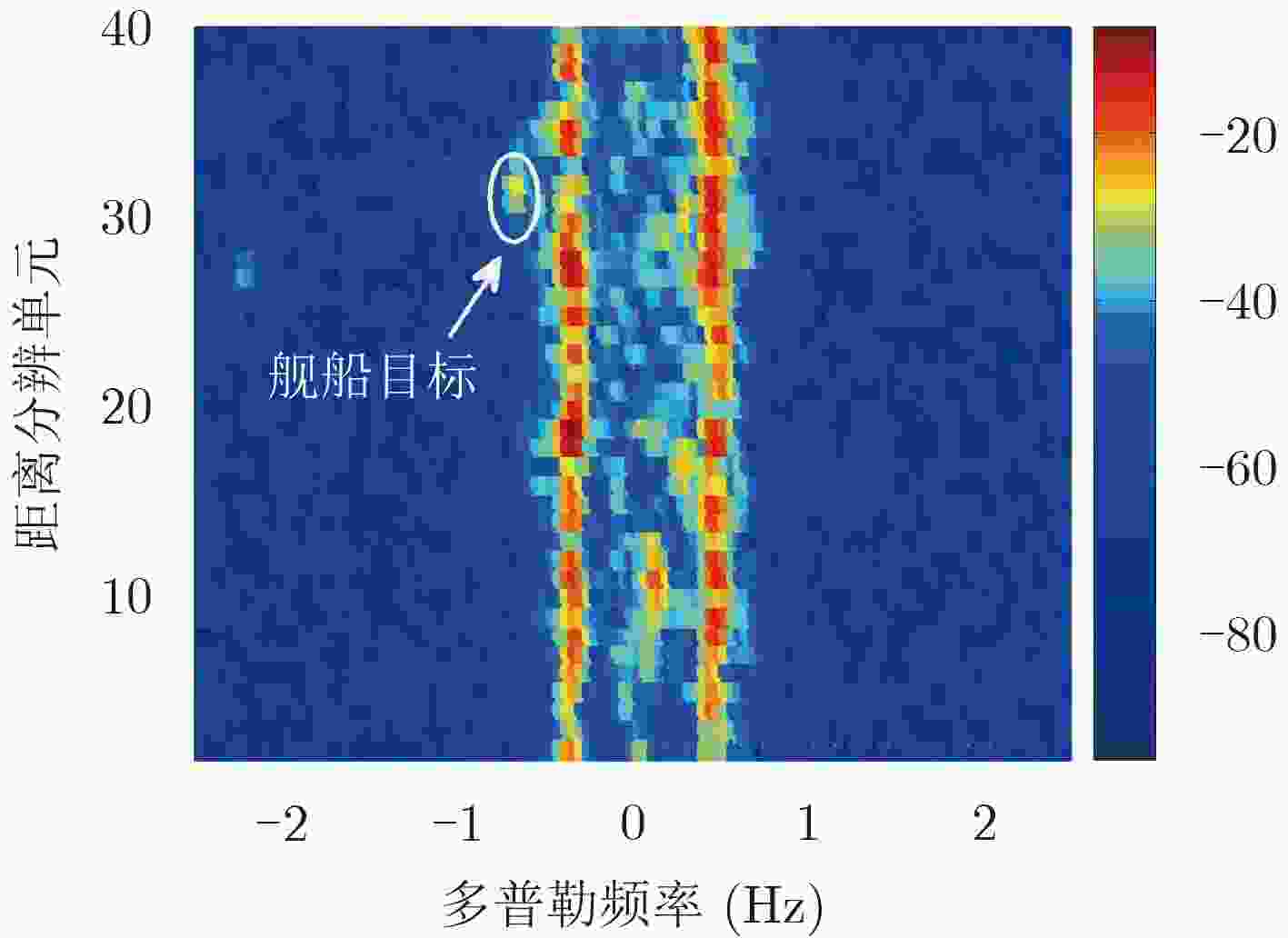
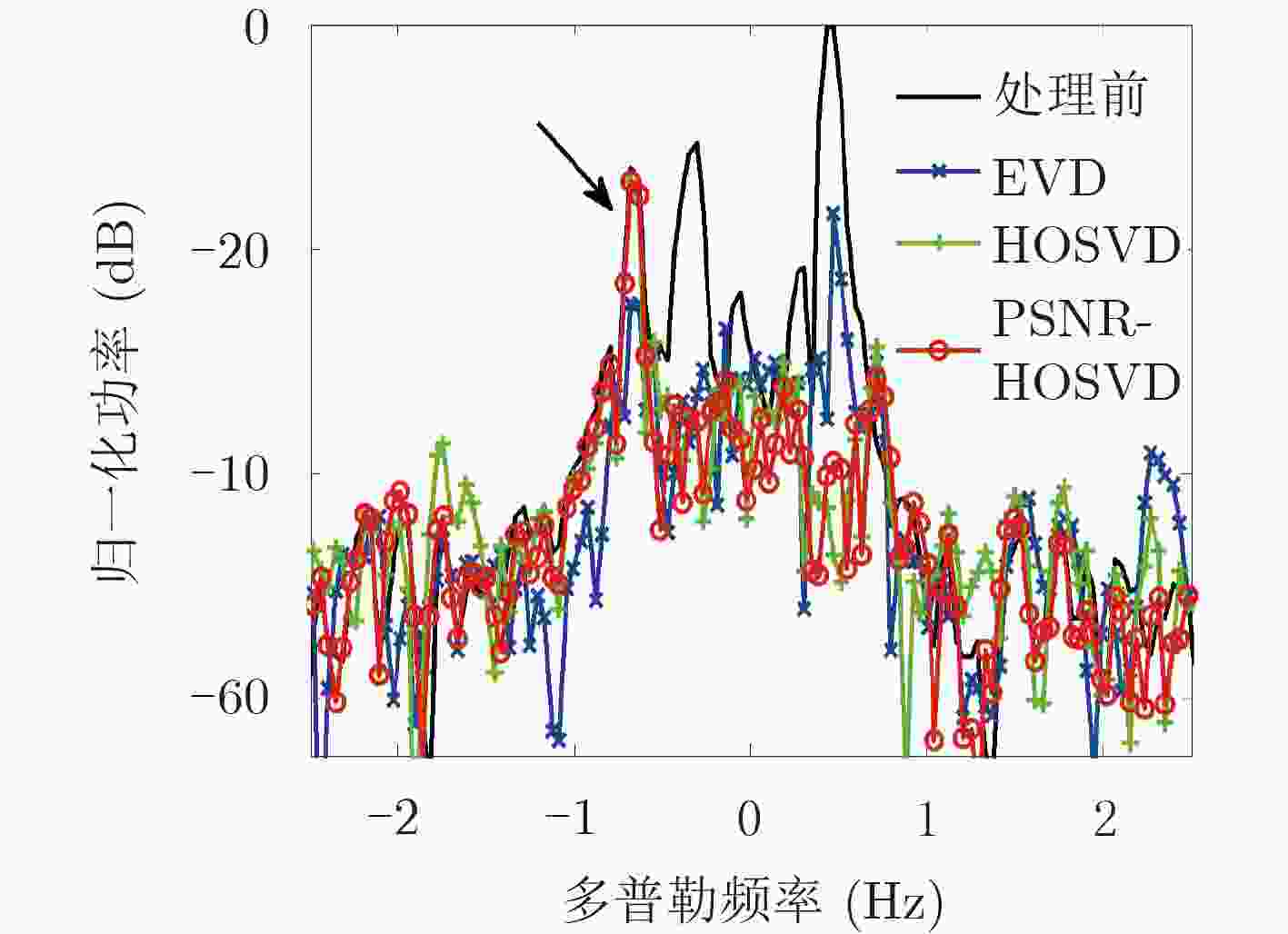
摘要: 天波超视距雷达(OTHR)舰船目标的检测性能受目标区海杂波的影响严重,准确且自适应的海杂波抑制效能对改善低可探测舰船目标的检测性能意义重大。该文针对基于高阶奇异值分解(HOSVD)的海杂波抑制算法非自适应机制的不足,通过引入峰值信噪比(PSNR),提出一种改进的基于PSNR-HOSVD的自适应算法。该算法仅利用第3等效模式展开矩阵的左奇异向量构造一个投影矩阵,相比于HOSVD算法,该文算法可有效降低计算复杂度,同时由于海杂波仅在第3等效模式展开矩阵的列空间中具有聚集特性,因此该文算法具有比HOSVD算法更好的海杂波抑制性能。实测数据处理结果表明,在电离层状态理想和非理想的情况下,该文PSNR-HOSVD自适应算法的性能均优于EVD自适应算法和HOSVD非自适应算法。Abstract: The detection performance of ship targets by skywave Over-The-Horizon Radar (OTHR) is affected by the sea clutter seriously. Accurate and adaptive suppression of sea clutter is significant for improving the detection performance of ship target. To solve the non-adaptive shortness of the sea clutter suppression algorithm based on High-Order Singular Value Decomposition (HOSVD), a modified adaptive algorithm based on Peak Signal-to-Noise Ratio (PSNR)-HOSVD is proposed by introducing the PSNR. The modified algorithm has a smaller computational complexity than the one based on HOSVD, since only one projection matrix is established from the left singular vectors of the third-mode unfolding matrix. Meanwhile, the modified algorithm has a better performance than the HOSVD based one, because the components of sea clutter are only aggregated in the column space of the third-mode unfolding matrix. Experimental results based on two sets of measured data received in ideal and non-ideal situations in respective show that, the modified adaptive algorithm based on PSNR-HOSVD has a better performance than the peer algorithms.
-
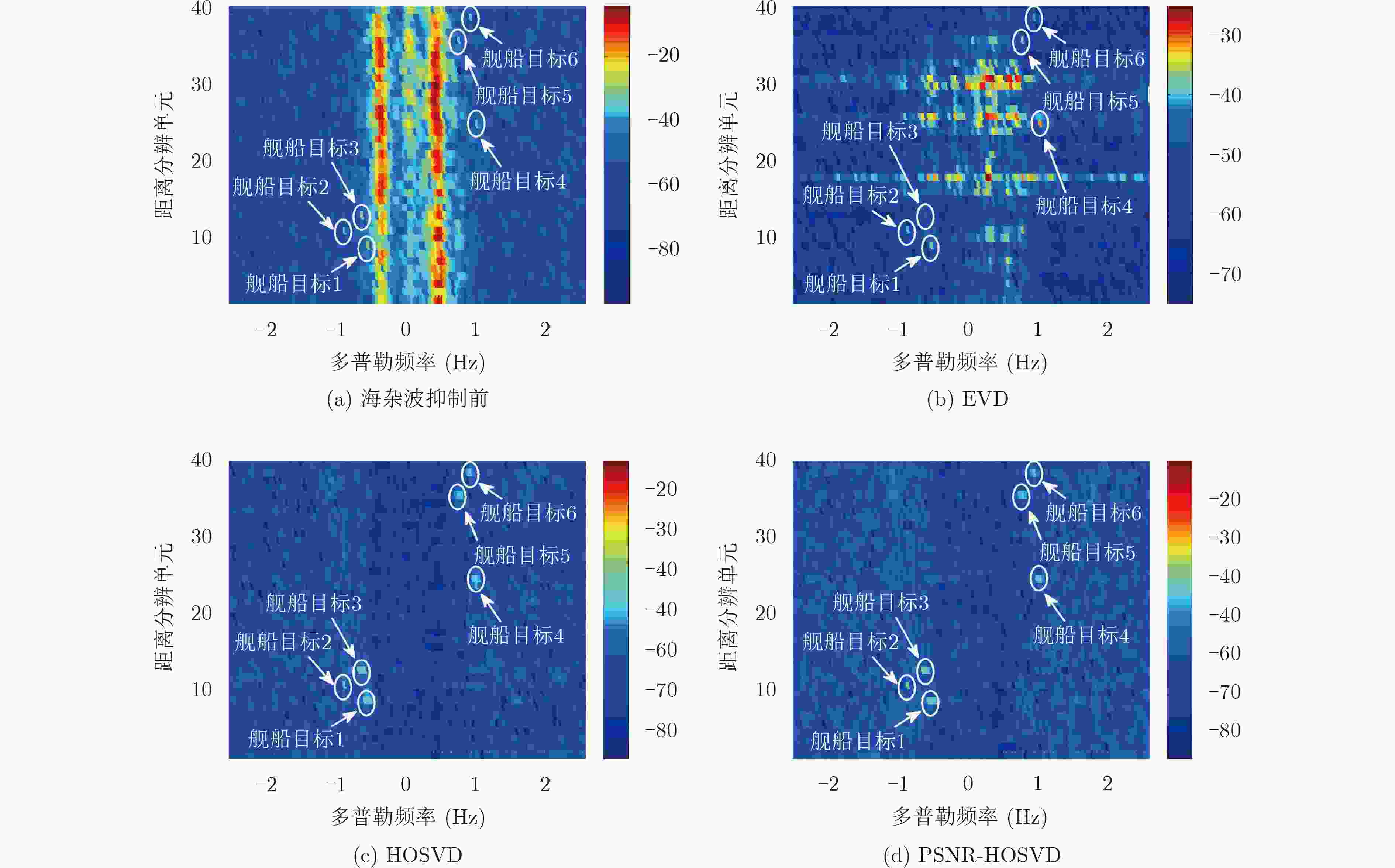
表 1 实验1各舰船目标参数
序号 1 2 3 4 5 6 距离分辨单元 8 10 12 24 35 38 多普勒频率(Hz) –0.55 –0.88 –0.64 0.96 0.72 0.88 SCNRin (dB) –11.49 –28.31 –18.85 –24.75 –22.44 –19.24 表 2 电离层状态理想时3种算法的处理结果中各舰船目标的输出SCNR和ISCNR (dB)
序号 1 2 3 4 5 6 均值 EVD算法 SCNRout 3.94 –4.15 6.00 1.77 –0.32 1.76 1.50 ISCNR 15.43 24.16 24.85 26.52 22.12 21.00 22.35 HOSVD算法 SCNRout 8.43 13.54 12.80 9.40 4.87 10.43 9.91 ISCNR 19.92 41.85 31.65 34.15 27.31 29.67 30.76 PSNR-HOSVD算法 SCNRout 9.06 13.89 12.48 10.56 5.66 8.72 10.06 ISCNR 20.55 42.20 31.33 35.31 28.10 27.96 30.91 -
周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 6–10.ZHOU Wenyu and JIAO Peinan. Technology for Over-the-Horizon Radar[M]. Beijing: Publishing House of Electronics Industry, 2008: 6–10. LUO Zhongtao, HE Zishu, CHEN Xuyuan, et al. Target location and height estimation via multipath signal and 2D array for sky-wave over-the-horizon radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(2): 617–631. doi: 10.1109/TAES.2015.140046 WU Xia, CHEN Jianwen, and LU Kun. Investigation of system structure and information processing mechanism for cognitive skywave over-the-horizon radar[J]. Journal of Systems Engineering and Electronics, 2016, 27(4): 797–806. doi: 10.21629/JSEE.2016.04.08 李雪, 郭晓彤, 王岳松, 等. 基于已知传播模式数目的海杂波抑制方法研究[J]. 电波科学学报, 2016, 31(4): 700–706. doi: 10.13443/j.cjors.2015110902LI Xue, GUO Xiaotong, WANG Yuesong, et al. Sea clutter suppression algorithm based on ionospheric propagation mode number[J]. Chinese Journal of Radio Science, 2016, 31(4): 700–706. doi: 10.13443/j.cjors.2015110902 关泽文, 陈建文, 鲍拯. 一种改进的天波雷达海杂波循环对消方法[J]. 空军预警学院学报, 2014, 28(5): 318–322. doi: 10.3969/j.issn.2095-5839.2014.05.002GUAN Zewen, CHEN Jianwen, and BAO Zheng. Modified method of sea clutter cancellation for sky wave radar[J]. Journal of Air Force Early Warning Academy, 2014, 28(5): 318–322. doi: 10.3969/j.issn.2095-5839.2014.05.002 严韬, 陈建文, 鲍拯. 一种基于压缩感知的天波超视距雷达短时海杂波抑制方法[J]. 电子与信息学报, 2017, 39(4): 945–952. doi: 10.11999/JEIT160576YAN Tao, CHEN Jianwen, and BAO Zheng. Sea clutter suppression method for over-the-horizon radar with short coherent integration time based on compressed sensing[J]. Journal of Electronics &Information Technology, 2017, 39(4): 945–952. doi: 10.11999/JEIT160576 王春雨, 卢庆广, 左雷, 等. 小型化地波雷达海杂波散射系数仿真及SVD抑制方法研究[J]. 舰船电子工程, 2013, 33(1): 86–93. doi: 10.3969/j.issn.1627-9730.2013.01.030WANG Chunyu, LU Qingguang, ZUO Lei, et al. Simulation of sea clutter scattering coefficient in miniaturized H-F surface radar and SVD method for suppressing[J]. Ship Electronic Engineering, 2013, 33(1): 86–93. doi: 10.3969/j.issn.1627-9730.2013.01.030 POON M W Y, KHAN R H, and LE-NGOC S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE Transactions on Signal Processing, 1993, 41(3): 1421–1425. doi: 10.1109/78.205747 陈俊斌, 卢琨, 刘兴钊. 天波雷达短驻留时间下海杂波抑制的改进算法[J]. 上海交通大学学报, 2004, 38(S1): 95–99. doi: 10.16183/j.cnki.jsjtu.2004.s1.024CHEN Junbin, LU Kun, and LIU Xingzhao. An improved ocean clutter cancellation algorithm with short dwells in sky-wave radars[J]. Journal of Shanghai Jiaotong University, 2004, 38(S1): 95–99. doi: 10.16183/j.cnki.jsjtu.2004.s1.024 WANG G, XIA X G, ROOT B T, et al. Manoeuvring target detection in over-the-horizon radar using adaptive clutter rejection and adaptive chirplet transform[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 292. doi: 10.1049/ip-rsn:20030700 蔚娜, 李雪, 李铁成. 基于特征分解的多模杂波抑制方法[J]. 电波科学学报, 2016, 31(1): 85–90. doi: 10.13443/j.cjors.2015021301WEI Na, LI Xue, and LI Tiecheng. An eigenvalue decomposition based method for suppressing multi-mode clutter[J]. Chinese Journal of Radio Science, 2016, 31(1): 85–90. doi: 10.13443/j.cjors.2015021301 薄超, 顾红, 苏卫民, 等. 基于高阶奇异值分解的天波雷达海杂波抑制算法[J]. 电波科学学报, 2014, 29(4): 715–722. doi: 10.13443/j.cjors.2013083001BO Chao, GU Hong, SU Weimin, et al. Over-the-horizon radar sea clutter suppression algorithm based on higher order singular value decomposition[J]. Chinese Journal of Radio Science, 2014, 29(4): 715–722. doi: 10.13443/j.cjors.2013083001 薄超, 顾红, 苏卫民. 基于高阶奇异值分解的OTHR海杂波抑制算法[J]. 系统工程与电子技术, 2014, 36(5): 872–878. doi: 10.3969/j.issn.1001-506X.2014.05.10BO Chao, GU Hong, and SU Weimin. OTHR sea clutter suppression algorithm based on higher order singular value decomposition[J]. Systems Engineering and Electronics, 2014, 36(5): 872–878. doi: 10.3969/j.issn.1001-506X.2014.05.10 赵志国, 陈建文, 鲍拯. 一种改进的OTHR自适应海杂波抑制方法[J]. 系统工程与电子技术, 2012, 34(5): 909–914. doi: 10.3969/j.issn.1001-506X.2012.05.10ZHAO Zhiguo, CHEN Jianwen, and BAO Zheng. Modified adaptive ocean clutter suppression approach in OTHR[J]. Systems Engineering and Electronics, 2012, 34(5): 909–914. doi: 10.3969/j.issn.1001-506X.2012.05.10 关泽文, 陈建文, 鲍拯. 天波超视距雷达海杂波模型修正与特性分析[J]. 电子与信息学报, 2017, 39(12): 2881–2888. doi: 10.11999/JEIT170224GUAN Zewen, CHEN Jianwen, and BAO Zheng. Model modifying and characteristics analyzing of ocean clutter in skywave over-the-horizon radar[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2881–2888. doi: 10.11999/JEIT170224 严韬, 陈建文, 鲍拯. 基于WLS的OTHR短时自适应海杂波抑制方法[J]. 华中科技大学学报: 自然科学版, 2017, 45(8): 20–25. doi: 10.13245/j.hust.170805YAN Tao, CHEN Jianwen, and BAO Zheng. Adaptive sea clutter suppression method for OTHR with short coherent integration time based on weighted least square[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2017, 45(8): 20–25. doi: 10.13245/j.hust.170805 DE LATHAUWER L, DE MOOR B, and VANDEWALLE J. A multilinear singular value decomposition[J]. SIAM Journal on Matrix Analysis and Applications, 2000, 21(4): 1253–1278. doi: 10.1137/S0895479896305696 XU Yangyang. Fast algorithms for higher-order singular value decomposition from incomplete data[J]. arXiv: 1411.4324. LI Qingzhong, ZHANG Wandong, LI Ming, et al. Automatic detection of ship targets based on wavelet transform for HF surface wavelet radar[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 714–718. doi: 10.1109/LGRS.2017.2673806 -







 下载:
下载:



 下载:
下载:
