Adaptive Design of Limiters for Impulsive Noise Suppression
-
摘要:
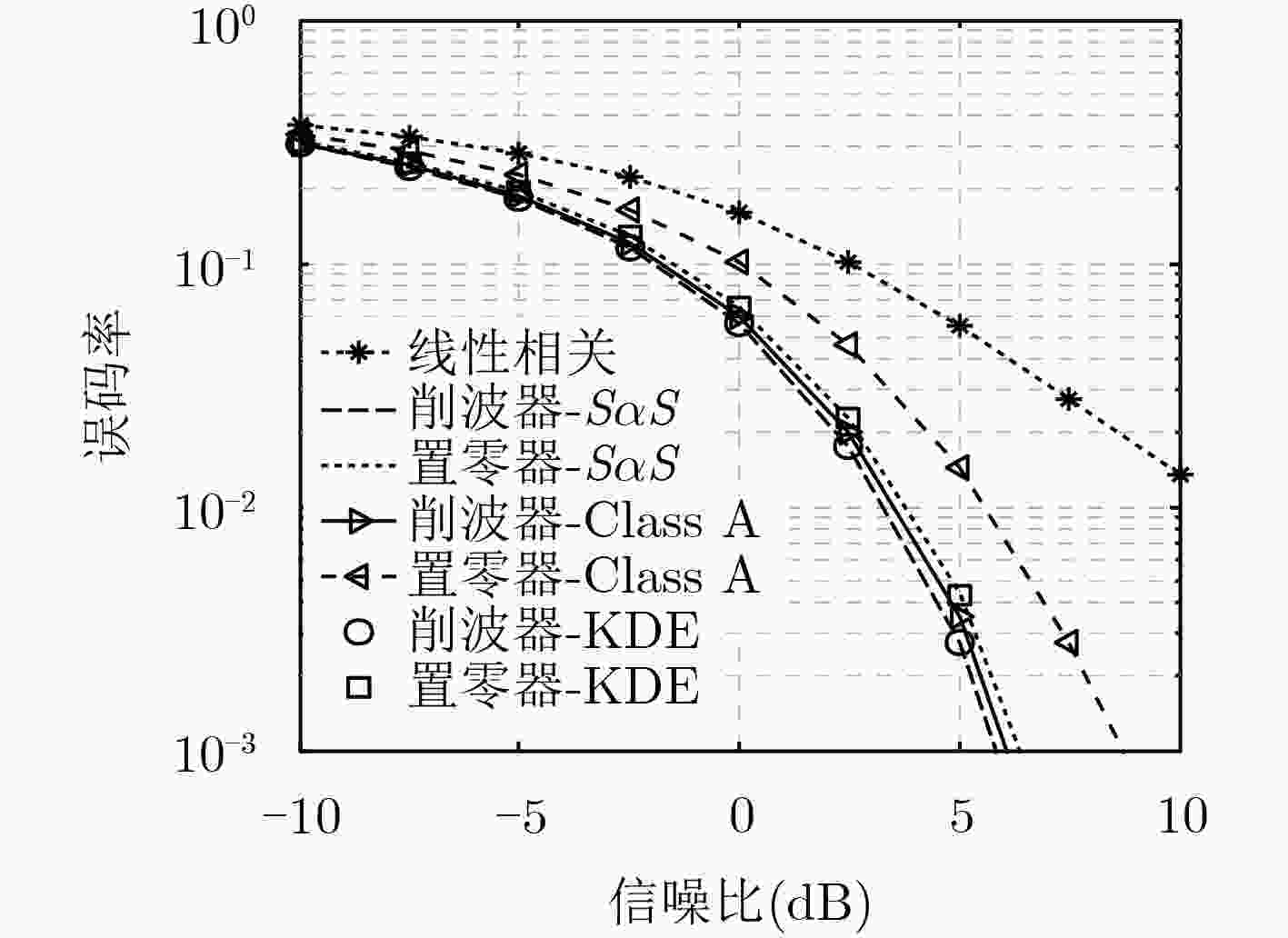
针对脉冲型噪声的抑制问题,该文提出一种自适应的限幅器设计方法。该方法以效能函数为指标,采用自适应搜索算法,自动寻找削波器和置零器的最佳门限,且能适用于未知噪声分布的情形。首先分析了效能与非线性函数的关系,给出关键的优化问题。然后考虑到效能函数计算复杂,提出基于线搜索的自适应设计算法。其次针对未知分布情况,考虑非参数化的概率密度估计,该算法能够稳健运行且基本取得最优设计效果。最后,结合两种非高斯噪声和实测大气噪声数据仿真,结果表明:该文方法可自适应寻找最佳门限,使削波器和置零器效能达到最佳;当噪声分布未知时,该文方法无需假设噪声模型,可与非参数化概率密度估计方法结合,取得最优检测效果。
Abstract:An adaptive method of limiter design is proposed to suppress impulsive noise. With a purpose of maximizing the efficacy function, the proposed method searches for optimal thresholds of clipper and blanker, via adaptive line search. Firstly, based on analysis on the relationship between the efficacy and the nonlinearity, the key problem of optimization is proposed. Then, since the calculation of efficacy is hard, an adaptive algorithm based on linear search approach is developed based on linear search to optimize the efficacy. Considering the noise distribution is unknown, the proposed method employs the nonparametric kernel density estimation and works robustly in the presence of estimation error. Finally, numeric simulations demonstrate that the proposed method can obtain the optimal performance of clippers and blankers successfully. In the processing of real atmospheric noise from unknown distribution, the proposed method achieves the best detection performance when combining nonparametric kernel density estimation approach.
-
Key words:
- Nonlinear processing /
- Efficiency function /
- Adaptive optimization /
- Clipper /
- Blanker
-
表 1 限幅器的自适应优化处理算法
步骤 1 设置初始值${\tau _0} > 0$,初始步长${d_0} = 0.5{\tau _0}$,迭代次数
$k = 0$,计算效能值${\eta _0} = \eta (g, f, {\tau _0})$;步骤 2 令${\tau _{k + 1}} = {\tau _k} + {d_k}$,并计算效能值${\eta _{k{\rm{ + 1}}}} = \eta (g, f, {\tau _{k + 1}})$。若
${\eta _{k{\rm{ + 1}}}} > {\eta _k}$,转步骤3;否则,转步骤4;步骤 3 正向搜索。令${d_{k + 1}} = 2{d_k}$, $\tau = {\tau _k}$, ${\tau _k} = {\tau _{k + 1}}$, ${\eta _k} = {\eta _{k{\rm{ + 1}}}}$,
$k = k + 1$,转步骤2;步骤 4 反向搜索。若$k = 0$,则令${d_1} = - {d_0}$, $\tau = {\tau _1}$, ${\tau _1} = {\tau _0}$,
${\eta _1} = {\eta _0}$, $k = 1$,转步骤2;否则,停止迭代;步骤 5 设置线搜索参数,容许误差比率$\lambda $。迭代次数j=0;令
${l_0} = {\rm{min}}\{ \tau, {\tau _{k + 1}}\} $, ${r_0} = {\rm{max}}\{ \tau, {\tau _{k + 1}}\} $, ${p_0} = {l_0} $
$ 0.382\left( {{r_0} - {l_0}} \right)$, ${q_0} = {l_0} + 0.618\left( {{r_0} - {l_0}} \right)$;步骤 6 条件判断。若$\eta (g, f, {p_j}) \ge \eta (g, f, {q_j})$,转步骤7,否则转
步骤8;步骤 7 计算左试探点。若$|{q_j} - {l_j}|/{r_j} > \lambda $,则令${l_{j + 1}} = {l_j}$, ${r_{j + 1}} $
$ ={q_j}$, $\eta (g, f, {q_{j + 1}}) = \eta (g, f, {p_j})$, ${q_{j + 1}} = {p_j}$, ${p_{j + 1}} = $
$ {l_{j + 1}} + 0.382({r_{j + 1}} - {l_{j + 1}})$,计算效能值$\eta (g, f, {p_{j + 1}})$,
$j = j + 1$,转步骤6;否则,停止搜索并
输出最佳门限值${p_j}$;步骤 8 计算右试探点。若$|{r_j} - {p_j}{\rm{|/}}{r_j} > \lambda $,则令${l_{j + 1}} = {p_j}$, ${r_{j + 1}} $
$={r_j}$, $\eta (g, f, {p_{j + 1}}) = \eta (g, f, {q_j})$, ${p_{j + 1}} = {q_j}$, ${q_{j + 1}} =$
$ {l_{j + 1}} + 0.618({r_{j + 1}} - {l_{j + 1}})$,计算效能值$\eta (g, f, {q_{j + 1}})$,
$j = j + 1$,转步骤6;否则,停止搜索并输
出最佳门限值${q_j}$。表 2 Class A分布下(
${A}{,} {Γ} $ )-${τ} $ 变化,${{σ}^2}$ =1$A, {\rm{ }}\varGamma $ $0.1, {\rm{ }}{10^{ - 3}}$ $0.35, {\rm{ }}{10^{ - 3}}$ $0.5, {\rm{ }}{10^{ - 3}}$ $0.1, {\rm{ }}{10^{ - 2}}$ $0.35, {\rm{ }}{10^{ - 2}}$ $0.5, {\rm{ }}{10^{ - 2}}$ ${\tau _{{\rm{opt\_}}b}}{\rm{ - PDF}}$(${\eta _{{\rm{opt\_}}b}}$) 0.1296(888.8429) 0.1094(647.4406) 0.0996(532.3140) 0.3397(87.5188) 0.2898(59.1912) 0.2698(46.5176) ${\tau _{{\rm{opt\_}}c}}{\rm{ - PDF}}$(${\eta _{{\rm{opt\_}}c}}$) 0.0386(671.5877) 0.0232(356.9533) 0.0188(257.2668) 0.1181(69.5440) 0.0743(38.4601) 0.0623(28.4378) ${\tau _{{\rm{opt\_}}b}}{\rm{ - KDE}}$(${\eta _{{\rm{opt\_}}b}}$) 0.1199(877.9385) 0.1094(631.7642) 0.0994(510.9088) 0.3494(85.5270) 0.2937(57.2562) 0.2708(43.9273) ${\tau _{{\rm{opt\_}}c}}{\rm{ - KDE}}$(${\eta _{{\rm{opt\_}}c}}$) 0.0396(665.3161) 0.0239(349.5658) 0.0197(247.0483) 0.1197(68.3936) 0.0786(36.7663) 0.0651(26.4190) 表 3
$\rm S{α} S$ 分布下限幅器自适应设计方法迭代次数$\alpha $ 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 Iterb-PDF 15 15 15 15 15 15 15 15 15 Iterc-PDF 17 17 17 16 16 16 16 15 15 Iterb-KDE 15 15 15 15 15 15 15 15 14 Iterc-KDE 17 17 17 16 16 16 16 15 15 -
KAY S M. Fundamentals of Statistical Signal Processing, Volume II: Detection Theory[M]. Englewood Cliffs, USA: Prentice-Hall, Inc., 1993: 94–115. DAVIS R R and CLAVIER O. Impulsive noise: A brief review[J]. Elsevier Hearing Research, 2017, 349: 34–36. doi: 10.1016/j.heares.2016.10.020 LI Xutao, SUN Jun, WANG Shouyong, et al. Near-optimal detection with constant false alarm ratio in varying impulsive interference[J]. IET Signal Processing, 2013, 7(9): 824–832. doi: 10.1049/iet-spr.2013.0024 MILLER J and THOMAS J. Detectors for discrete-time signals in non-Gaussian noise[J]. IEEE Transactions on Information Theory, 1972, 18(2): 241–250. doi: 10.1109/TIT.1972.1054787 VADALI S R K, RAY P, MULA S, et al. Linear detection of a weak signal in additive Cauchy noise[J]. IEEE Transactions on Communications, 2017, 65(3): 1061–1076. doi: 10.1109/TCOMM.2016.2647599 WANG Pingbo, LIU Feng, CAI Zhiming, et al. G-Filter's Gaussianization function for interference background[C]. International Conference on Signal Acquisition and Processing, Nanjing, China, 2010: 76–79. 罗忠涛, 卢鹏, 张杨勇, 等. 基于高斯化-广义匹配的脉冲型噪声处理方法研究[J]. 电子与信息学报, 2018, 40(12): 2928–2935. doi: 10.11999/JEIT180191LUO Zhongtao, LU Peng, ZHANG Yangyong, et al. A novel method for nonlinear processing in impulsive noise based on gaussianization and generalized matching[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2928–2935. doi: 10.11999/JEIT180191 OH H and NAM H. Design and performance analysis of nonlinearity preprocessors in an impulsive noise environment[J]. IEEE Transactions on Vehicular Technology, 2017, 66(1): 364–376. doi: 10.1109/TVT.2016.2547889 OH H, NAM H, and PARK S. Adaptive threshold blanker in an impulsive noise environment[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(5): 1045–1052. doi: 10.1109/TEMC.2014.2311853 KOLODZIEJSKI K R and BETZ J W. Detection of weak random signals in IID non-Gaussian noise[J]. IEEE Transactions on Communications, 2000, 48(2): 222–230. doi: 10.1109/26.823555.doi:10.1109/26.823555 ZHANG Guoyong, WANG Jun, YANG Guosheng, et al. Nonlinear processing for correlation detection in symmetric alpha-stable noise[J]. IEEE Signal Processing Letters, 2018, 25(1): 120–124. doi: 10.1109/LSP.2017.2776317 张杨勇, 刘勇. 低频段大气噪声及处理技术[J]. 舰船科学技术, 2008, 30(S1): 85–88. doi: 10.3404/j.issn.1672-7649.2008.S021ZHANG Yangyong and LIU Yong. Atmospheric-noise at low frequency and its processing technique[J]. Ship Science &Technology, 2008, 30(S1): 85–88. doi: 10.3404/j.issn.1672-7649.2008.S021 MODESTINO J W and NINGO A Y. Detection of weak signals in narrowband non-Gaussian noise[J]. IEEE Transactions on Information Theory, 1979, 25(5): 592–600. doi: 10.1109/TIT.1979.1056086 KURUOGLU E E, FITZGERALD W J, and RAYNER P J W. Near optimal detection of signals in impulsive noise modeled with a symmetric alpha-stable distribution[J]. IEEE Communications Letters, 1998, 2(10): 282–284. doi: 10.1109/4234.725224 VASTOLA K. Threshold detection in narrow-band non-Gaussian noise[J]. IEEE Transactions on Communications, 1984, 32(2): 134–139. doi: 10.1109/TCOM.1984.1096037 CHONG E K D and ZAK S H. An Introduction to Optimization[M]. Hoboken, New Jersey: John Wiley & Sons, 2014: 105–108. NOCEDAL J and WRIGHT S J. Numerical Optimization[M]. New York NY, US: Springer-Verlag Inc., 1999: 35–62. SCALES L E. Introduction to Non-Linear Optimization[M]. London, UK: Macmillan Publishers, 1985: 31–34. SAMIUDDIN M and EL-SAYYAD G M. On nonparametric kernel density estimates[J]. Biometrika, 1990, 77(4): 865–874. doi: 10.1093/77.4.865 SILVERMAN B W. Density Estimation for Statistics and Data Analysis[M]. London, UK: Chapman & Hall, 1986: 45–48. HE Jiai, DU Panpan, and CHEN Xing. Parameter estimation of communication signal in alpha-stable distribution noise environment[C]. Computational Intelligence and Security, Hong Kong, China, 2017: 15–18. BIBALAN M H, AMINDAVAR H, and AMIRMAZLAGHANI M. Characteristic function based parameter estimation of skewed alpha-stable distribution: An analytical approach[J]. Elsevier Signal Processing, 2017, 130: 323–336. doi: 10.1016/j.sigpro.2016.07.020 MIDDLETON D. Procedures for determining the parameters of the first-order canonical models of Class A and Class B electromagnetic interference[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 21(3): 190–208. doi: 10.1109/TEMC.1979.303731 AXELL E, ELIARDSSON P, TENGSTRAND S, et al. Power control in interference channels with Class A impulse noise[J]. IEEE Wireless Communications Letters, 2017, 6(1): 102–105. doi: 10.1109/LWC.2016.2634529 -





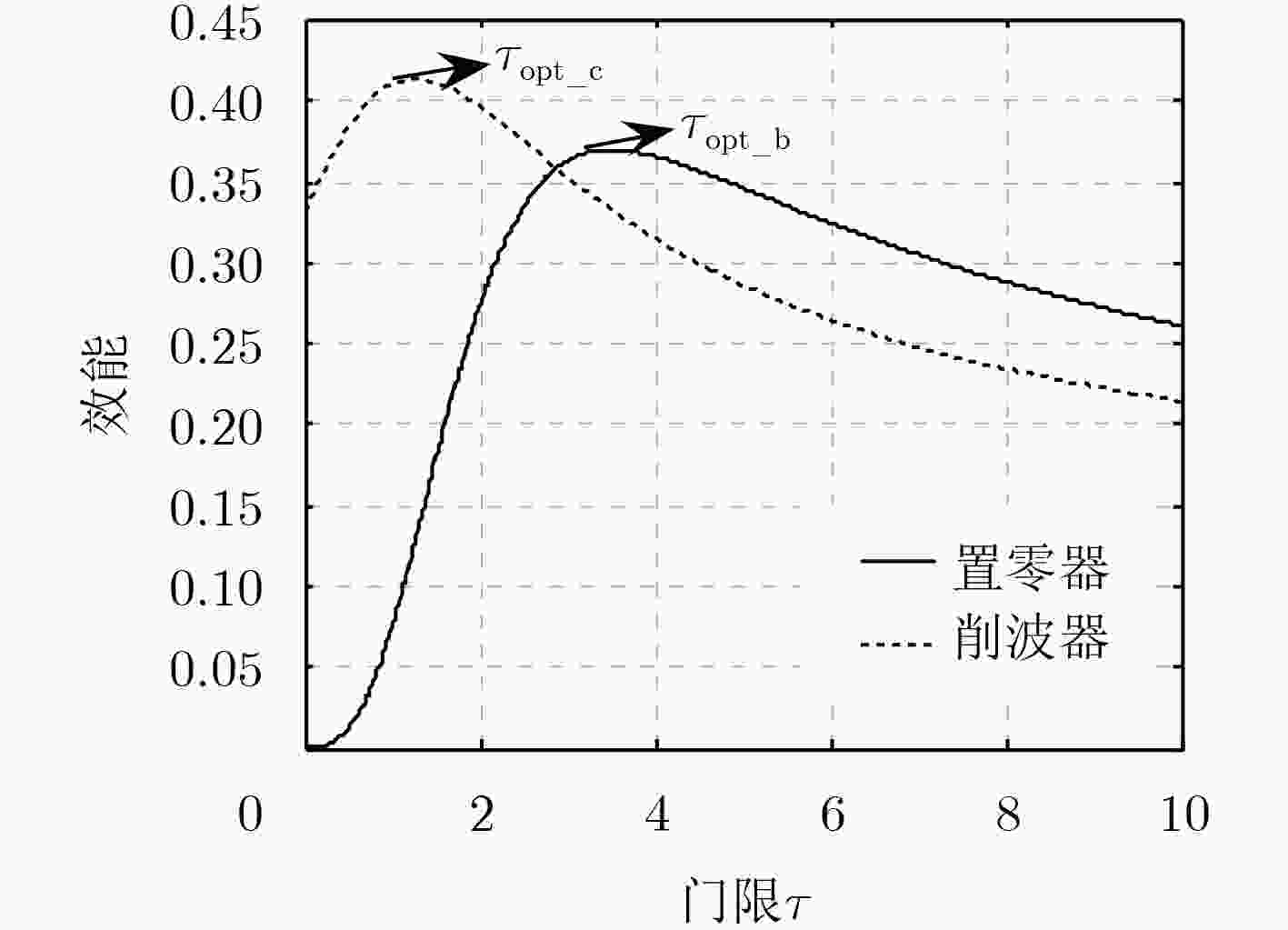



 下载:
下载:
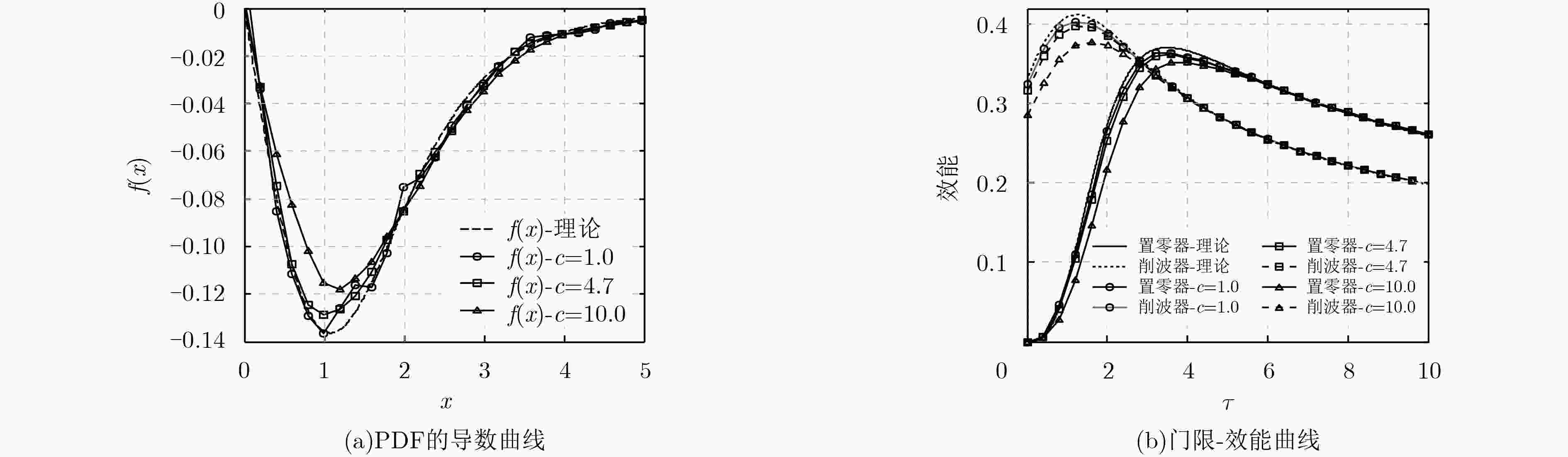



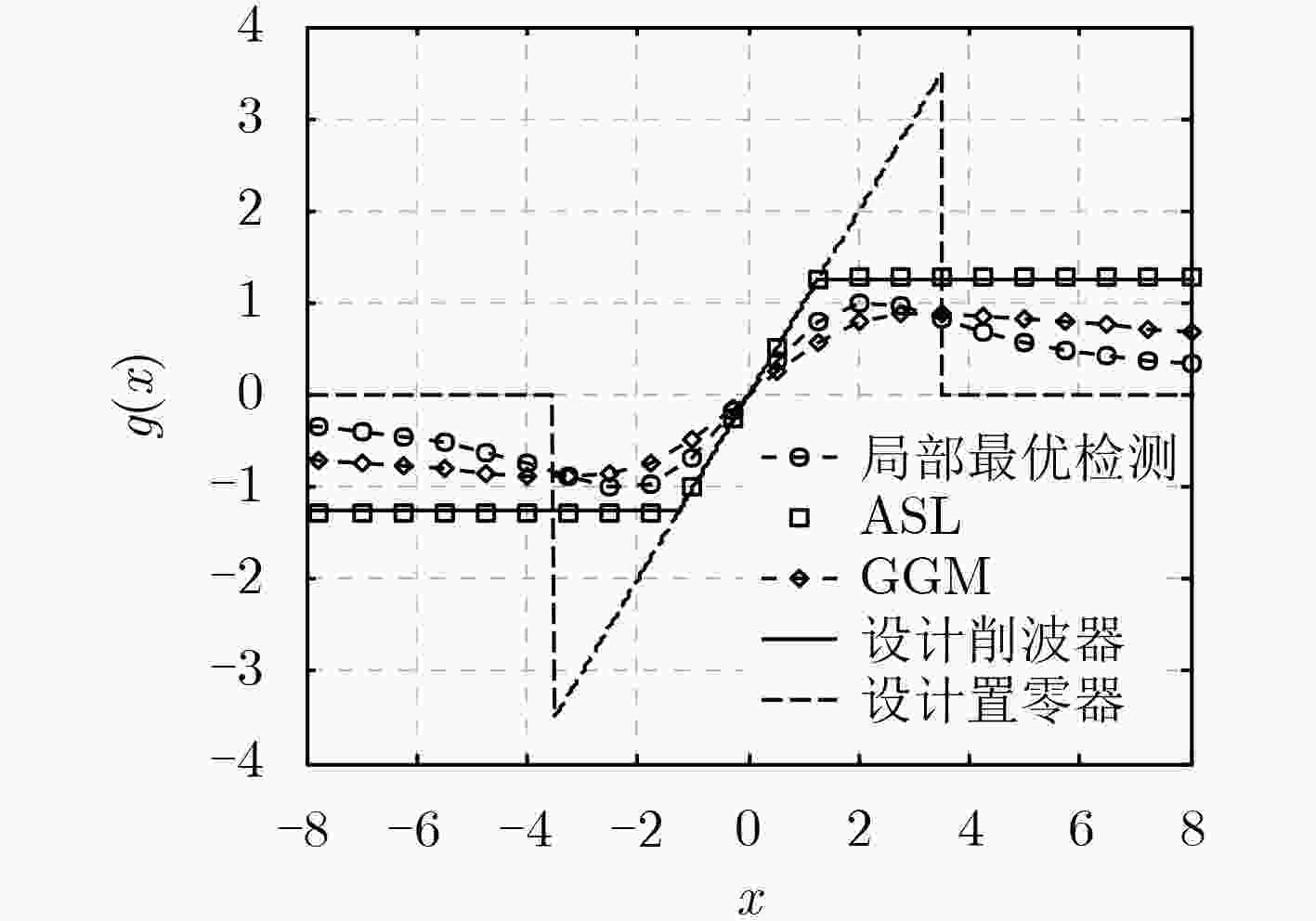


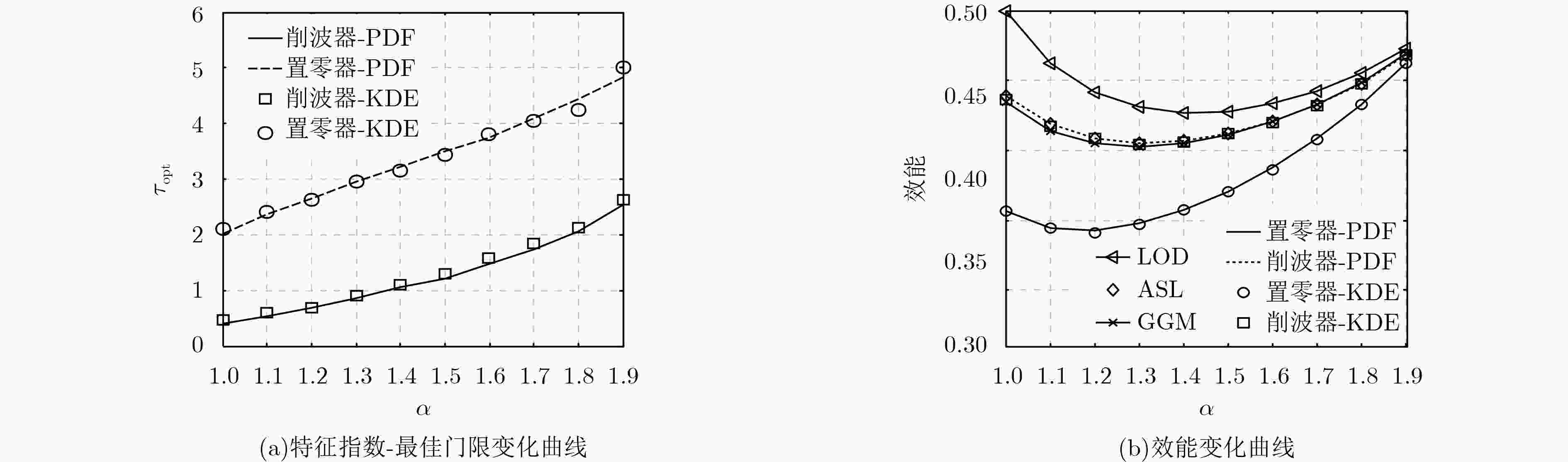








 下载:
下载:
