Robust Fuzzy C-means Clustering Algorithm Integrating Between-cluster Information
-
摘要:
与经典的K均值聚类算法相比,模糊C均值(FCM)聚类算法通过引入模糊因子,考虑不同聚类数据簇之间的相互关系,得到可分性更好的聚类结果。但是模糊因子的引入,使得任意一个样本点都存在模糊性,造成FCM极易受到噪声和离群点的影响,聚类结果泛化性能较差。因此,该文提出一种簇间可分的鲁棒FCM算法(RBI-FCM)。RBI-FCM利用K均值算法对模糊隶属度的稀疏特征,降低不同数据簇之间的相互作用,突出不同数据簇相邻区域的可分性;另外,RBI-FCM在极小化数据簇内部散布度的条件下,考虑不同数据簇之间的可分性,可提高聚类模型的泛化性能。该文设计了有效的模型求解迭代算法。实验结果表明,RBI-FCM算法提高了FCM的鲁棒性,有效降低FCM对数据簇分布差异性和抽样不均衡的敏感性,得到理想的聚类结果。
Abstract:Comparing with K-means, Fuzzy logic is introduced in Fuzzy C-Means to handle the information between clusters. It can obtain better cluster results. However, fuzzy logic makes observations could belong to more than just one cluster, which results FCM is especially sensitivity to the noisy and outlier and has poor generalization performance. So a Rrobust Fuzzy C-Means clustering integrated Between-cluster Information algorithm (RBI-FCM) is proposed. Taking advantage of the sparsity of K-means, RBI-FCM helps to reduce the interactions among different clusters and improve the separability of sample points which locate in the adjacent domains of different clusters. Beside minimizing the inner-cluster scattering condition, RBI-FCM considers the between-cluster information. The generalization performance of RBI-FCM can be improved. An effective iterative algorithm for solving the model is designed in this paper. The experimental results show that the RBI-FCM improves the robustness of FCM and reduce effectively its sensitivity to size-imbalance and differences on the distribution of clusters of FCM. The great clustering result is obtained.
-
Key words:
- Clustering /
- Fuzzy C-Means (FCM) /
- Sample distribution /
- Between-cluster information
-
表 1 实验1:人造样本数据集主要参数
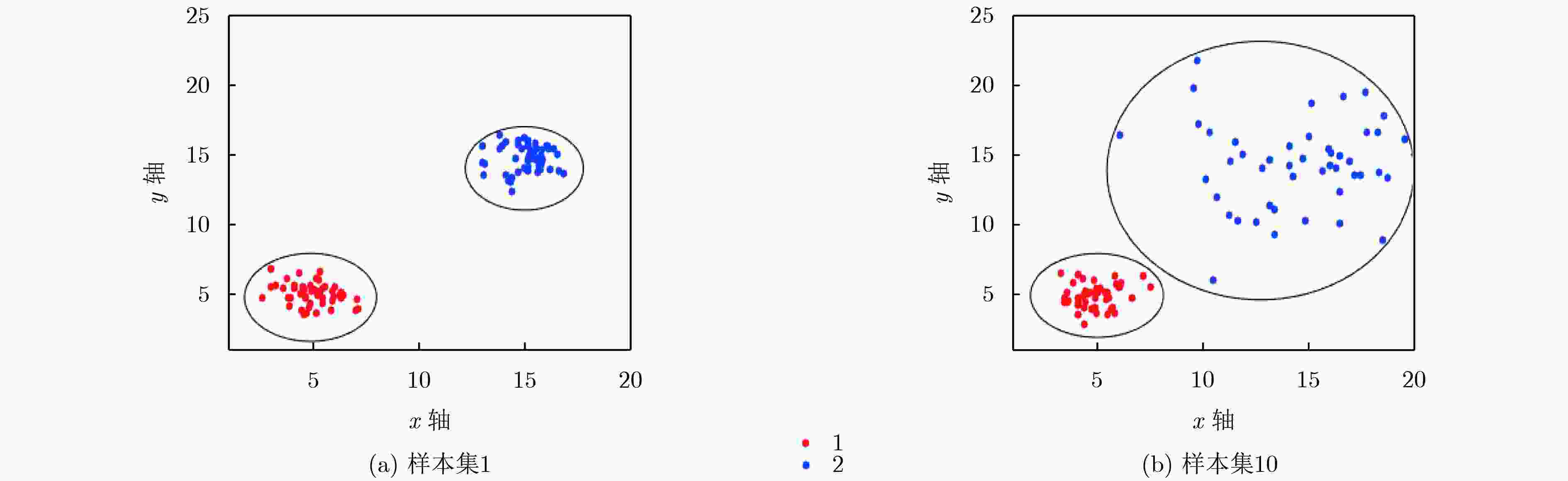
样本集 类中心 协方差矩阵 各类样本数 1 (5, 5), (15, 15) [1 0; 0 1], [1 0; 0 1] 50, 50 2 (5, 5), (15, 15) [1 0; 0 1], [2 0; 0 2] 50, 50 $\vdots $ $\vdots $ $\vdots $ $\vdots $ 10 (5, 5), (15, 15) [1 0; 0 1], [10 0; 0 10] 50, 50 表 2 实验2:人造样本数据集主要参数
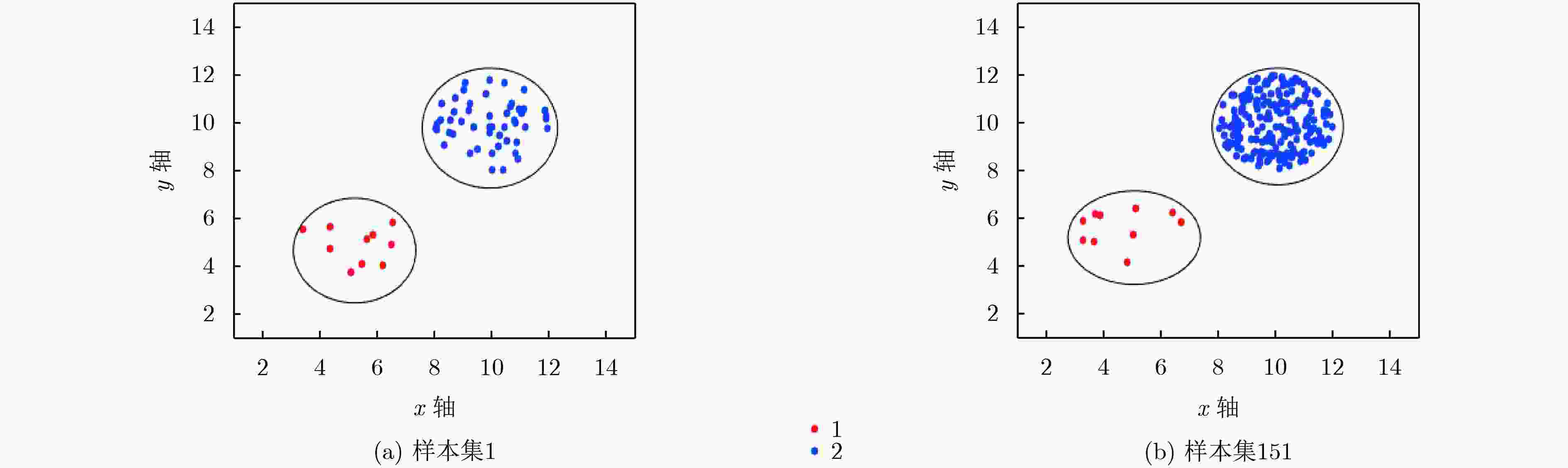
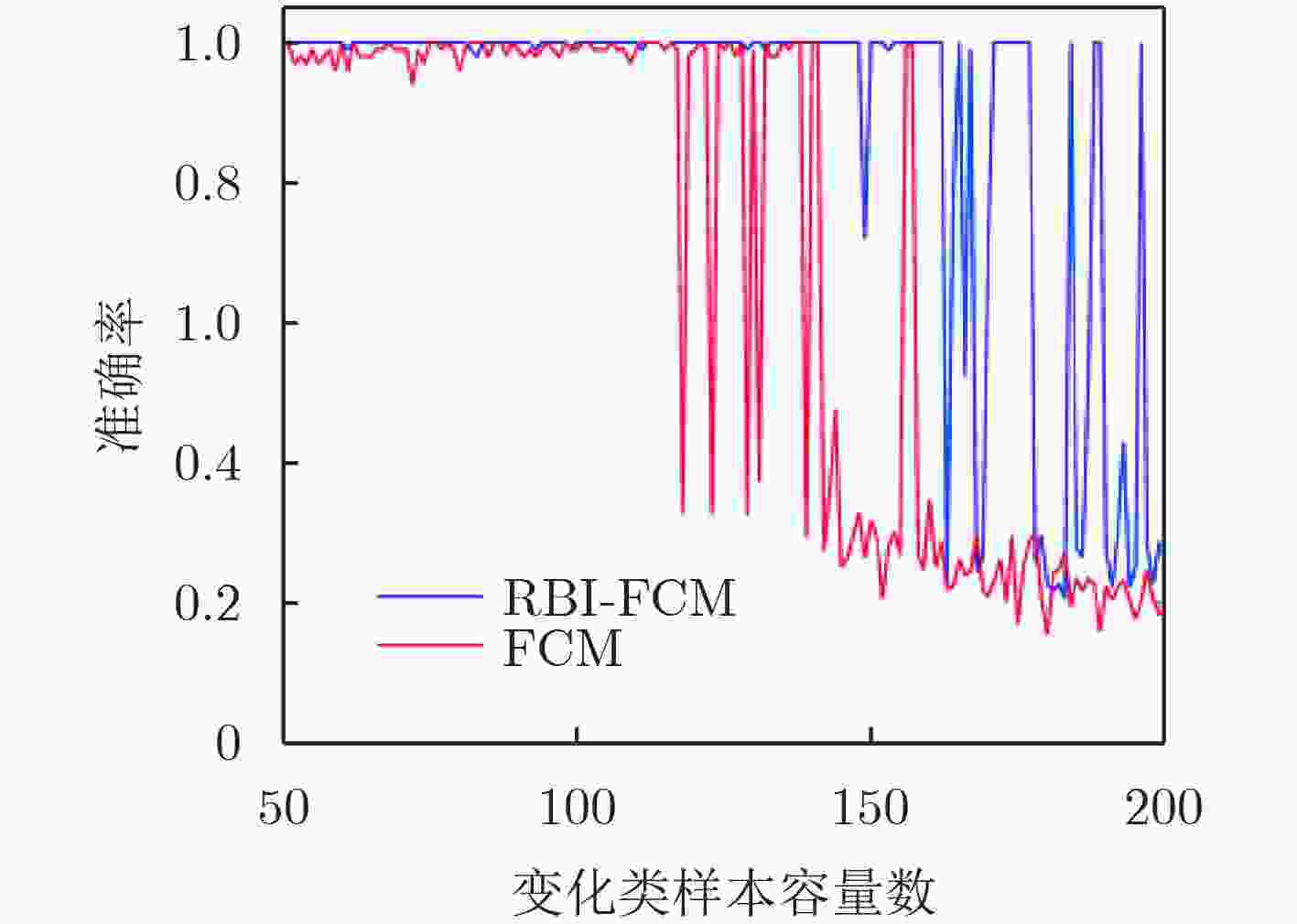
样本集 样本随机分布的圆心 各类样本数 1 (5, 5), (15, 15) 50, 50 2 (5, 5), (15, 15) 50, 51 $\vdots $ $\vdots $ $\vdots $ $\vdots $ 151 (5, 5), (15, 15) 50, 200 表 3 UCI数据集聚类实验的NMI正确率和RI正确率
UCI数据集 FCM PFCM GIFP-FCM RBI-FCM UCI数据集 FCM PFCM GIFP-FCM RBI-FCM Auto-mgp 0.5190 0.5167 0.5008 0.5443 Wine 0.4169 0.4168 0.3946 0.4911 0.7534 0.7537 0.7505 0.7895 0.7104 0.7105 0.6700 0.7287 Zoo 0.6760 0.6824 0.6284 0.6873 Balance Scale 0.1223 0.1232 0.1293 0.1326 0.8381 0.8400 0.8236 0.8464 0.5887 0.5900 0.5806 0.5947 Parkinsons 0.0926 0.0936 0.0526 0.1071 House Votes 0.4743 0.4743 0.2917 0.4948 0.5934 0.5934 0.5693 0.6266 0.7752 0.7752 0.6688 0.7890 Credit Approval 0.0304 0.0304 0.0365 0.1020 Vowel 0.3019 0.3127 0.3357 0.3737 0.5048 0.5048 0.5207 0.5448 0.7755 0.7988 0.8275 0.8153 Banknote Authentication 0.0292 0.0292 0.1145 0.5249 Mammographic Masses 0.1054 0.1065 0.1020 0.1130 0.5236 0.5236 0.5555 0.8053 0.5676 0.5683 0.5524 0.5746 注:每个数据集实验结果的第1行为NMI正确率,第2行为RI正确率 -
陈新泉, 周灵晶, 刘耀中. 聚类算法研究综述[J]. 集成技术, 2017, 6(3): 41–49. doi: 10.3969/j.issn.2095-3135.2017.03.004CHEN Xinquan, ZHOU Lingjing, and LIU Yaozhong. Review on clustering algorithms[J]. Journal of Integrati on Technology, 2017, 6(3): 41–49. doi: 10.3969/j.issn.2095-3135.2017.03.004 张传锦, 李璐璐. 基于模糊C均值聚类的无线传感器网络节点定位算法[J]. 电子设计工程, 2016, 24(8): 58–60. doi: 10.14022/j.cnki.dzsjgc.2016.08.017ZHANG Chuanjin and LI Lulu. Improving multilateration algorithm based on fuzzy C-means cluster in WSN[J]. Electronic Design Engineering, 2016, 24(8): 58–60. doi: 10.14022/j.cnki.dzsjgc.2016.08.017 池桂英, 王忠华. 基于分层的直觉模糊C均值聚类图像分割算法[J]. 计算机工程与设计, 2017(12): 3368–3373. doi: 10.16208/j.issn1000-7024.2017.12.031CHI Guiying and WANG Zhonghua. Intuitionistic fuzzy C-means clustering algorithm based on hierarchy for image segmentation[J]. Computer Engineering and Design, 2017(12): 3368–3373. doi: 10.16208/j.issn1000-7024.2017.12.031 黄艳国, 罗云鹏. 基于改进模糊C均值聚类算法的城市道路状态判别方法[J]. 科学技术与工程, 2018, 18(9): 335–342. doi: 10.3969/j.issn.1671-1815.2018.09.052HUANG Yanguo and LUO Yunpeng. Identification method of urban road condition based on improved fuzzy C-means method clustering algorithm[J]. Science Technology and Engineering, 2018, 18(9): 335–342. doi: 10.3969/j.issn.1671-1815.2018.09.052 赵泉华, 刘晓燕, 赵雪梅, 等. 基于可变类FCM算法的多光谱遥感影像分割[J]. 电子与信息学报, 2018, 40(1): 157–165. doi: 10.11999/JEIT170397ZHAO Quanhua, LIU Xiaoyan, ZHAO Xuemei, et al. Multispectral remote sensing image segmentation based on FCM algorithm with unknown number of clusters[J]. Journal of Electronics &Information Technology, 2018, 40(1): 157–165. doi: 10.11999/JEIT170397 XU Rui and WUNSCH D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 645–678. doi: 10.1109/tnn.2005.845141 陈海鹏, 申铉京, 龙建武, 等. 自动确定聚类个数的模糊聚类算法[J]. 电子学报, 2017, 45(3): 687–694. doi: 10.3969/j.issn.0372-2112.2017.03.028CHEN Haipeng, SHEN Xuanjing, LONG Jianwu, et al. Fuzzy clustering algorithm for automatic identification of clusters[J]. Acta Electronica Sinica, 2017, 45(3): 687–694. doi: 10.3969/j.issn.0372-2112.2017.03.028 YANG MiinShen and NATALIANI Y. Robust-learning fuzzy c-means clustering algorithm with unknown number of clusters[J]. Pattern Recognition, 2017, 71: 45–59. doi: 10.1109/nafips.2010.5548175 PAL N R, PAL K, KELLER J M, et al. A possibilistic fuzzy C-means clustering algorithm[J]. IEEE Transactions on Fuzzy Systems, 2005, 13(4): 517–530. doi: 10.1109/tfuzz.2004.840099 肖满生, 肖哲, 文志诚, 等. 一种空间相关性与隶属度平滑的FCM改进算法[J]. 电子与信息学报, 2017, 39(5): 1123–1129. doi: 10.11999/JEIT160710XIAO Mansheng, XIAO Zhe, WEN Zhicheng, et al. Improved FCM clustering algorithm based on spatial correlation and membership smoothing[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1123–1129. doi: 10.11999/JEIT160710 LIU Yun, HOU Tao, and LIU Fu. Improving fuzzy c-means method for unbalanced dataset[J]. Electronics Letters, 2015, 51(23): 1880–1882. doi: 10.1049/el.2015.1541 史慧峰, 马晓宁. 一种自适应的模糊C均值聚类算法[J]. 无线通信技术, 2016, 25(3): 40–45. doi: 10.3969/j.issn.1003-8329.2016.03.009SHI Huifeng and MA Xiaoning. An adaptive fuzzy C-means clustering algorithm[J]. Wireless Communication Technology, 2016, 25(3): 40–45. doi: 10.3969/j.issn.1003-8329.2016.03.009 曲福恒. 模糊聚类算法及应用[M]. 北京: 国防工业出版社, 2011.QU Fuheng. Fuzzy clustering algorithm and its application[M]. Beijing, National Defense Industry Press, 2011. DUNN J C. A fuzzy relative of the isodata process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1974, 3(3): 32–57. doi: 10.1080/01969727308546046 BEZDEK J C. Pattern Recognition with Fuzzy Objective Function Algorithms[J]. Springer US, 1981. doi: 10.1007/978-1-4757-0450-1 ZHU Lin, CHUNG FuLai, and WANG Shitong. Generalized fuzzy C-means clustering algorithm with improved fuzzy partitions[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A, 2009, 39(3): 578–591. doi: 10.3724/sp.j.1087.2013.02355 HÖPPNER F and KLAWONN F. Improved fuzzy partitions for fuzzy regression models[J]. International Journal of Approximate Reasoning, 2003, 32(2): 85–102. doi: 10.1016/s0888-613x(02)00078-6 DENG Zhaohong, CHOI K S, CHUNG Fulai, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern Recognition, 2010, 43(3): 767–781. doi: 10.1016/j.patcog.2009.09.010 -





 下载:
下载:


 下载:
下载:
