Parallel MoM Using the Six Hundred Thousand Cores on Domestically-made and Many-core Supercomputer
-
摘要:
为实现电磁计算的安全可靠和自主可控,该文基于“天河二号”国产众核超级计算机平台,开展大规模并行矩量法(MoM)的开发工作。为减轻大规模并行计算时计算机集群的通信压力以及加速矩量法积分方程求解,通过分析矩量法电场积分方程离散生成的矩阵具有对角占优特性,提出一种新型LU分解算法,即对角块矩阵选主元LU分解(BDPLU)算法,该算法减少了panel列分解的计算量,更重要的是,完全消除了选主元过程的MPI通信开销。利用BDPLU算法,并行矩量法突破了6×105 CPU核并行规模,这是目前在国产超级计算平台上实现的最大规模的并行矩量法计算,其矩阵求解并行效率可达51.95%。数值结果表明,并行矩量法可准确高效地在国产超级计算平台上解决大规模电磁问题。
Abstract:In order to realize safety, reliability and self-control of electromagnetic computing, the large-scale parallel MoM is studied based on domestically-made many-core supercomputer platform named " Tianhe-2”. A new LU decomposition algorithm named Block Diagonal matrix Pivoting LU decomposition (BDPLU) algorithm, is proposed by analyzing the diagonally dominant characteristics of the matrix generated through dispersing electric field integral equation of MoM, for the purpose of communication pressure reduction to computer cluster and solution acceleration to MoM integral equation during large-scale parallel computation. The BDPLU algorithm reduces the amount of calculation in the process of panel factorization. More importantly, the algorithm completely eliminates MPI communication when pivoting. Using BDPLU algorithm, the maximum number of CPU cores break through 6×105 CPU cores, which is the largest scale of parallel MoM computation in domestically-made and many-core supercomputing platform at present, and the parallel efficiency of solving matrix can reach 51.95%. Numerical results show that parallel MoM can accurately and efficiently solve large-scale electromagnetic field problems on domestic supercomputing platform.
-
表 1 CALU算法与BDPLU算法矩阵求解时间对比
FT2000+核数 矩阵求解时间(s) 并行效率(%) CALU BDPLU CALU BDPLU 2000 796.54 742.57 100 100 3000 567.78 518.68 93.53 95.44 4000 463.93 421.12 85.85 88.17 5000 386.89 338.24 82.35 87.82 10000 226.57 187.83 70.31 79.07 15000 172.91 139.05 61.42 71.20 20000 133.97 118.38 59.46 62.73 40000 72.83 64.61 54.68 57.47 表 2 BDPLU算法求解矩阵的加速比和并行效率
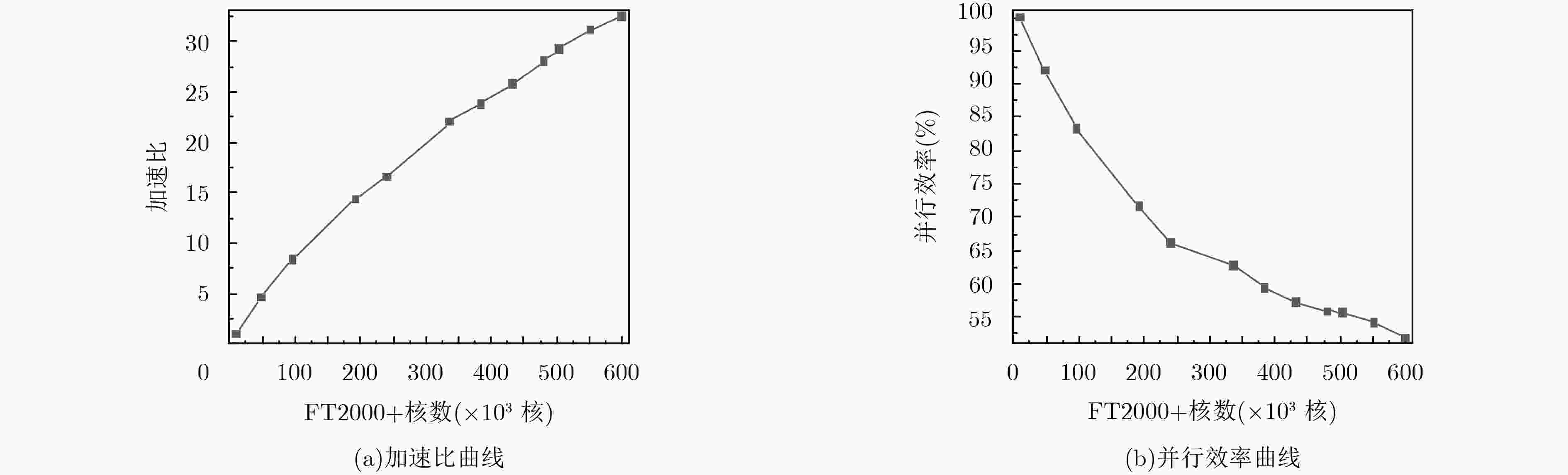
FT2000+核数 矩阵求解时间(s) 加速比 并行效率(%) 9600 29183.33 1 100 48000 6336.53 4.61 92.11 96000 3501.73 8.33 83.34 192000 2035.35 14.34 71.69 240000 1764.53 16.54 66.16 336000 1328.13 21.97 62.78 384000 1227.91 23.77 59.42 432000 1133.64 25.74 57.21 480000 1043.45 27.97 55.94 504000 997.94 29.24 55.70 552000 937.82 31.12 54.12 600000 898.81 32.49 51.95 -
HARRINGTION R F. Field Computation by Moment Methods[M]. New York; IEEE Press, 1993. 王长清. 现代计算电磁学基础[M]. 北京: 北京大学出版社, 2005: 116–157.WANG Changqing. Computational Advanced Electromagnetics[M]. Beijing: PeKing University Press, 2005: 116–157. ZHANG Yu and SARKAR T K. Parallel Solution of Integral Equation Based EM Problems in the Frequency Domain [M].Hoboken, USA: Wiley-IEEE, 2009: 107–136. 张玉, 赵勋旺, 陈岩, 等. 计算电磁学中的大规模并行矩量法[M]. 西安: 西安电子科技大学出版社, 2016: 11210.ZHANG Yu, ZHAO Xunwang, CHEN Yan, et al. Massively Parallel Method of Moment in Computational Electromagnetics[M].Xi’an: Xidian University Press, 2016: 11210. 林中朝, 张爽, 王星, 等. 高阶矩量法在国产超级计算机上的并行性能[J]. 微波学报, 2014, 30(S1): 44–47LIN Zhongchao, ZHANG Shuang, WANG Xing, et al. Parallel performance of higher-order MoM on a domestically-made supercomputer[J]. Journal of Microwaves, 2014, 30(S1): 44–47 林中朝, 陈岩, 张玉, 等. 国产CPU平台中并行高阶矩量法研究[J]. 西安电子科技大学学报, 2015, 42(3): 43–47 doi: 10.3969/j.issn.1001-2400.2015.03.008LIN Zhongchao, CHEN Yan, ZHANG Yu, et al. Study of the parallel higher-order MoM on a domestically-made CPU platform[J]. Journal of Xidian University, 2015, 42(3): 43–47 doi: 10.3969/j.issn.1001-2400.2015.03.008 ZHANG Yu, LIN Zhongchao, ZHAO Xunwang, et al. Performance of a massively parallel higher-order method of moment code using thousands of CPUs and its applications[J]. IEEE Transactions on Antenna Propagation, 2014, 62(12): 6317–6324 doi: 10.1109/TAP.2014.2361135 ZHAO Xunwang, CHEN Yan, ZHANG Huanhuan, et al. A New Decomposition Solver for Complex Electromagnetic Problems[J]. IEEE Antennas & Propagation Magazine, 2017, 59(3): 131–140 doi: 10.1109/MAP.2017.2687119 CHEN Yan, ZHANG Yu, ZHANG Guanghui, et al. Hybrid MIC/CPU parallel implementation of MoM on MIC cluster for electromagnetic problems[J]. IEICE Transactions on Electronics, 2016, 99(7): 735–743 doi: 10.1587/transele.E99.C.735 CHEN Yan, ZHANG Guanghui, LIN Zhongchao, et al. Solution of EM problems using hybrid parallel MIC/CPU implementation of higher-order MoM[C]. IEEE International Symposium on Microwave, Antenna, Propagation, and Emc Technologies. Shanghai, China, 2016: 789–791. 左胜, 陈岩, 张玉, 等. 一种可扩展异构并行核外高阶矩量法[J]. 西安电子科技大学学报, 2017, 44(1): 146–151 doi: 10.3969/j.issn.1001-2400.2017.01.026ZUO Sheng, CHEN Yan, ZHANG Yu, et al. Study of the scalable heterogeneous parallel out-of-core higher order method of moments[J]. Journal of Xidian University, 2017, 44(1): 146–151 doi: 10.3969/j.issn.1001-2400.2017.01.026 CHEN Yan, ZUO Sheng, ZHANG Yu, et al. Large-scale parallel method of moments on CPU/MIC heterogeneous clusters[J]. IEEE Transactions on Antennas & Propagation, 2017, 65(7): 3782–3787 doi: 10.1109/TAP.2017.2700871 TANG Min, ZHAO Jieyi, TONG Ruofeng, et al. GPU accelerated convex hull computation[J]. Computers & Graphics, 2012, 36(5): 498–506 doi: 10.1016/j.cag.2012.03.015 陈岩. 高性能矩量法及其在复杂目标电磁模拟中的应用[D]. [博士论文], 西安电子科技大学, 2017: 86–91.Chen Yan. High performance method of moments and its application in electromagnetic simulation of complex targets[D]. [Ph.D. dissertation], Xidian University, 2017: 86–91. ZHANG Yu, CHEN Yan, ZHANG Guanghui, et al. A highly efficient communication avoiding LU algorithm for Methods of Moments[C]. IEEE International Symposium on Antennas and Propagation & Usnc/ursi National Radio Science Meeting, Vancouver, Canada, 2015: 1672–1673. Intel® Developer Zone: Intel® Math Kernel Library [OL]. https://software.intel.com/en-us/forums/intel-math-kernel-library/, 2018. 徐晓飞, 曹祥玉, 高军, 等. 基于矩量法的电大目标RCS核外并行计算[J]. 电子与信息学报, 2011, 33(3): 758–762 doi: 10.3724/SP.J.1146.2010.00519XU Xiaofei, CAO Xiangyu, GAO Jun, et al. Parallel out-of-core calculation of electrically large objects’ RCS based on MoM[J]. Journal of Electronics &Information Technology, 2011, 33(3): 758–762 doi: 10.3724/SP.J.1146.2010.00519 马骥, 龚书喜, 王兴, 等. 一种快速计算目标宽带雷达截面的电磁算法[J]. 西安电子科技大学学报, 2012, 39(4): 98–102 doi: 10.3969/j.issn.1001-2400.2012.04.018MA Ji, GONG Shuxi, WANG Xing, et al. Fast computation of the wide-band radar cross section of arbitrary objects[J]. Journal of Xidian University, 2012, 39(4): 98–102 doi: 10.3969/j.issn.1001-2400.2012.04.018 国家超级计算广州中心: 产品中心[OL]. http://www.nscc-gz.cn/Product/HighPerformanceComputingService/ServiceCharacteristics.html, 2018.6. -





 下载:
下载:


 下载:
下载:
