Missing Data Prediction Based on Kronecker Compressing Sensing in Multivariable Time Series
-
摘要:
针对现有算法在预测多变量时间序列中的缺失数据时不适用或只适用于缺失数据较少的情况,该文提出一种基于克罗内克压缩感知的缺失数据预测算法。首先,利用多变量时间序列的时域平滑特性和序列之间的潜在相关性从时空两个方面设计了稀疏表示基,从而将缺失数据预测问题建模成稀疏向量恢复问题。模型求解部分,根据缺失数据的位置特点设计了适合当前应用场景且与稀疏表示基相关性低的观测矩阵。接着,从稀疏表示向量是否足够稀疏和感知矩阵是否满足有限等距特性两个方面验证了模型的性能。最后,仿真结果表明,所提算法在数据缺失严重的情况下具有良好的性能。
Abstract:In view of the problem that the existing methods are not applicable or are only feasible to the case where only a low ratio of data are missing in multivariable time series, a missing data prediction algorithm is proposed based on Kronecker Compressed Sensing (KCS) theory. Firstly, the sparse representation basis is designed to largely utilize both the temporal smoothness characteristic of time series and potential correlation between multiple time series. In this way, the missing data prediction problem is modeled into the problem of sparse vector recovery. In the solution part of the model, according to the location of missing data, the measurement matrix is designed suitable for the current application scenario and low correlation with the sparse representation basis. Then, the validity of the model is verified from two aspects: Whether the sparse representation vector is sufficiently sparse and the sensing matrix satisfies the restricted isometry property. Simulation results show that the proposed algorithm has good performance in the case where a high ratio of data are missing.
-
表 1 多变量时间序列
数据源 t1 t2 t3 t4 $\cdots$ tK s1 0.2 ? ? 0.3 1.9 s2 ? 0.4 0.5 ? ? s3 ? 0.7 ? 0.6 ? s4 0.8 ? ? ? 2.1 $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ sN ? 0.1 1.2 1.3 ? 表 2 稀疏表示基稀疏性能比较
n 100 200 300 500 MOTES_1 0.9897 0.9952 0.9973 0.9992 MOTES_2 0.7428 0.8731 0.9301 0.9786 GSA_1 0.9687 0.9995 0.9998 0.9999 GSA_2 0.5227 0.6841 0.9018 0.9721 SST_1 0.8759 0.9429 0.9722 0.9935 SST_2 0.7390 0.8785 0.9393 0.9849 表 3 稀疏表示基和观测矩阵非相关性的大小
NK 2000 3000 4000 6000 8000 $I({ {{ψ}}_R},{ {φ}_{{\rm{KCS}}1}})$ 1998 2995 3997 5996 7993 $I({ {{ψ}}_R},{ {φ}_{{\rm{KCS}}2}})$ 1998 2999 4000 5999 8000 $I({ {{ψ}}_E},{ {φ}_{{\rm{KCS}}1}})$ 1999 2996 3997 5999 7995 $I({ {{ψ}}_E},{ {φ}_{{\rm{KCS}}2}})$ 1999 2999 3999 6000 8000 $I({ {{ψ}}_C},{ {φ}_{{\rm{KCS}}1}})$ 1997 2996 3997 5995 7995 $I({ {{ψ}}_C},{ {φ}_{{\rm{KCS}}2}})$ 1998 2999 3998 5999 7998 表 4 各方法在不同数据缺失率下的性能比较
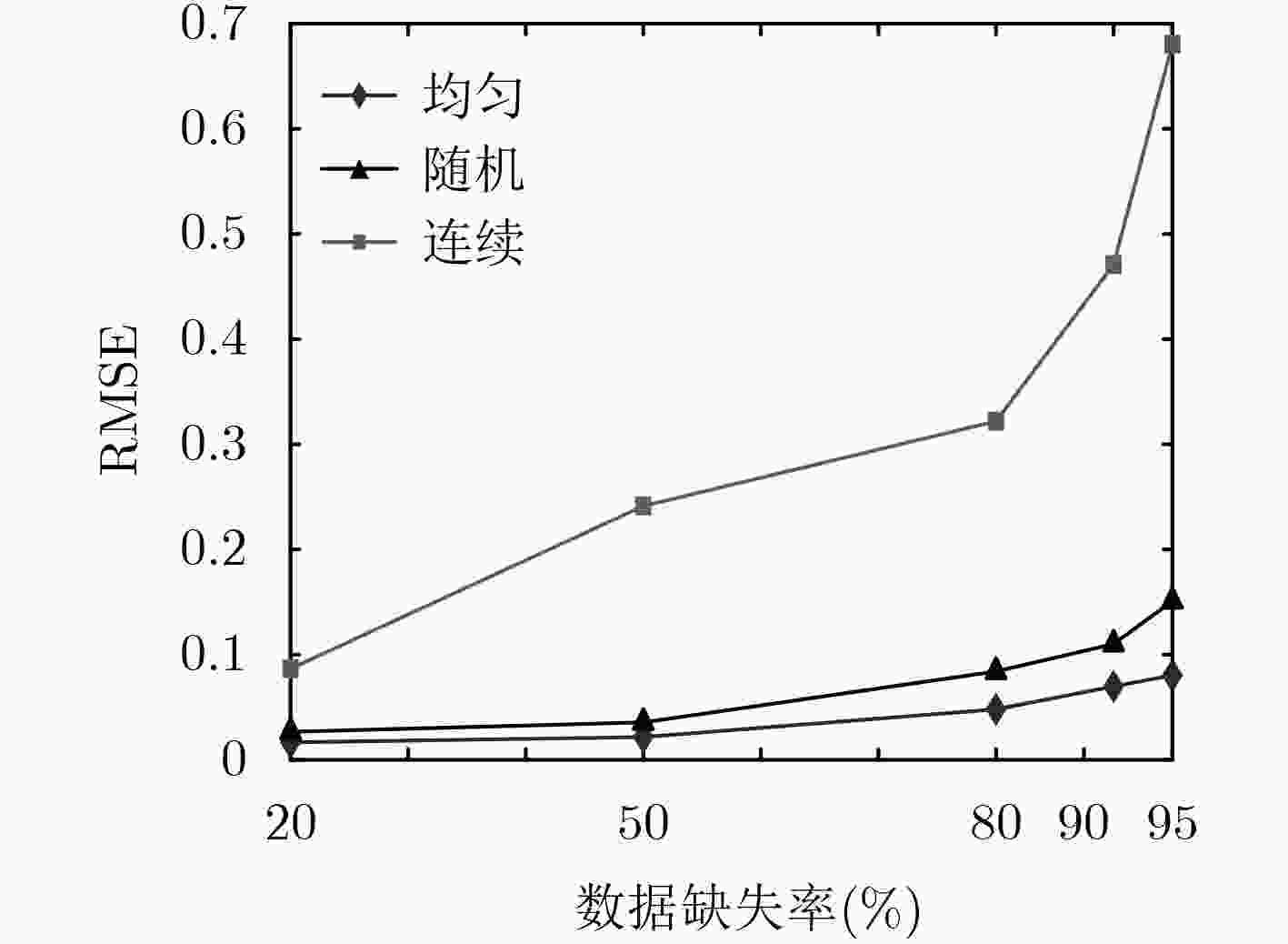
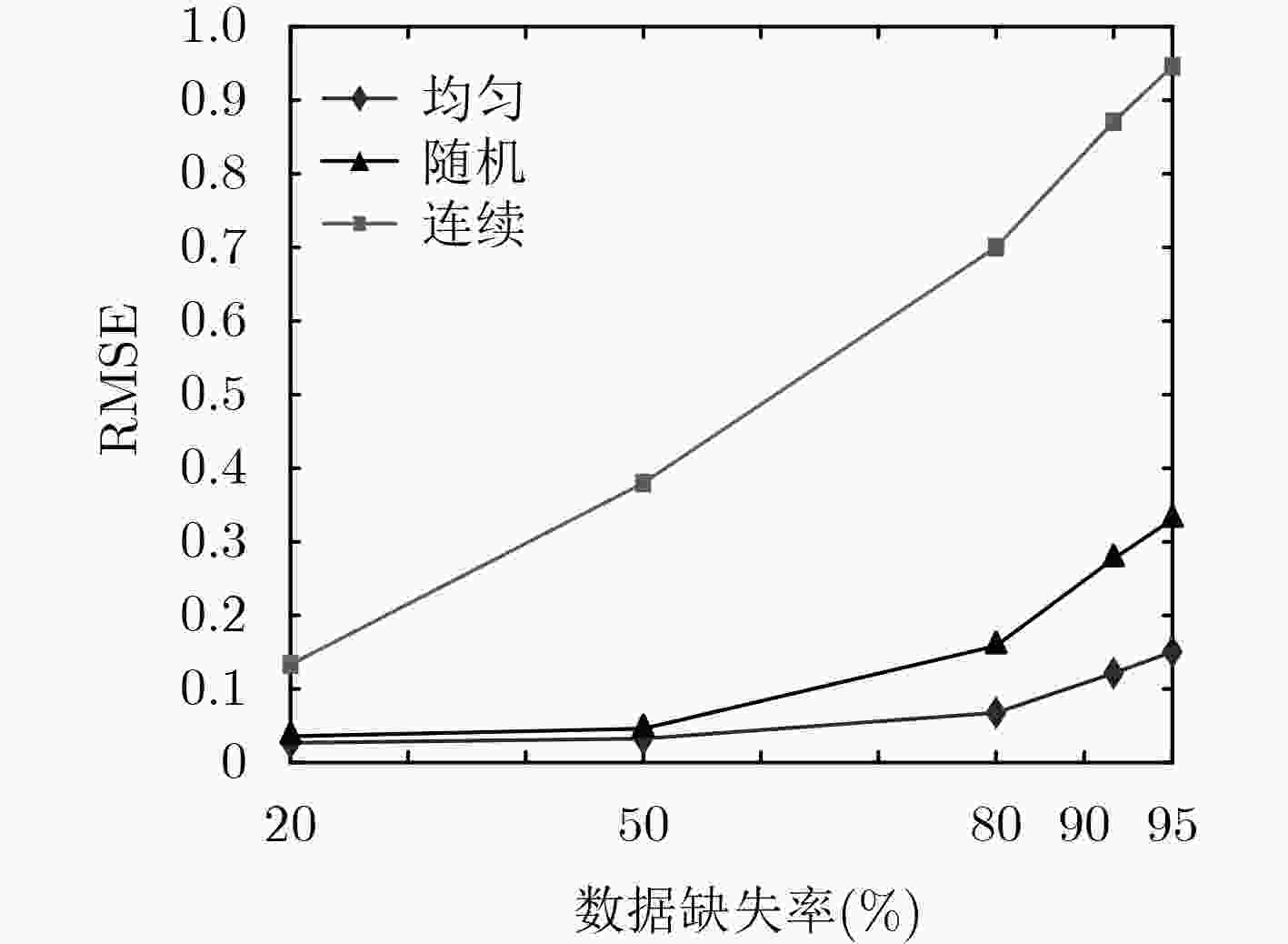
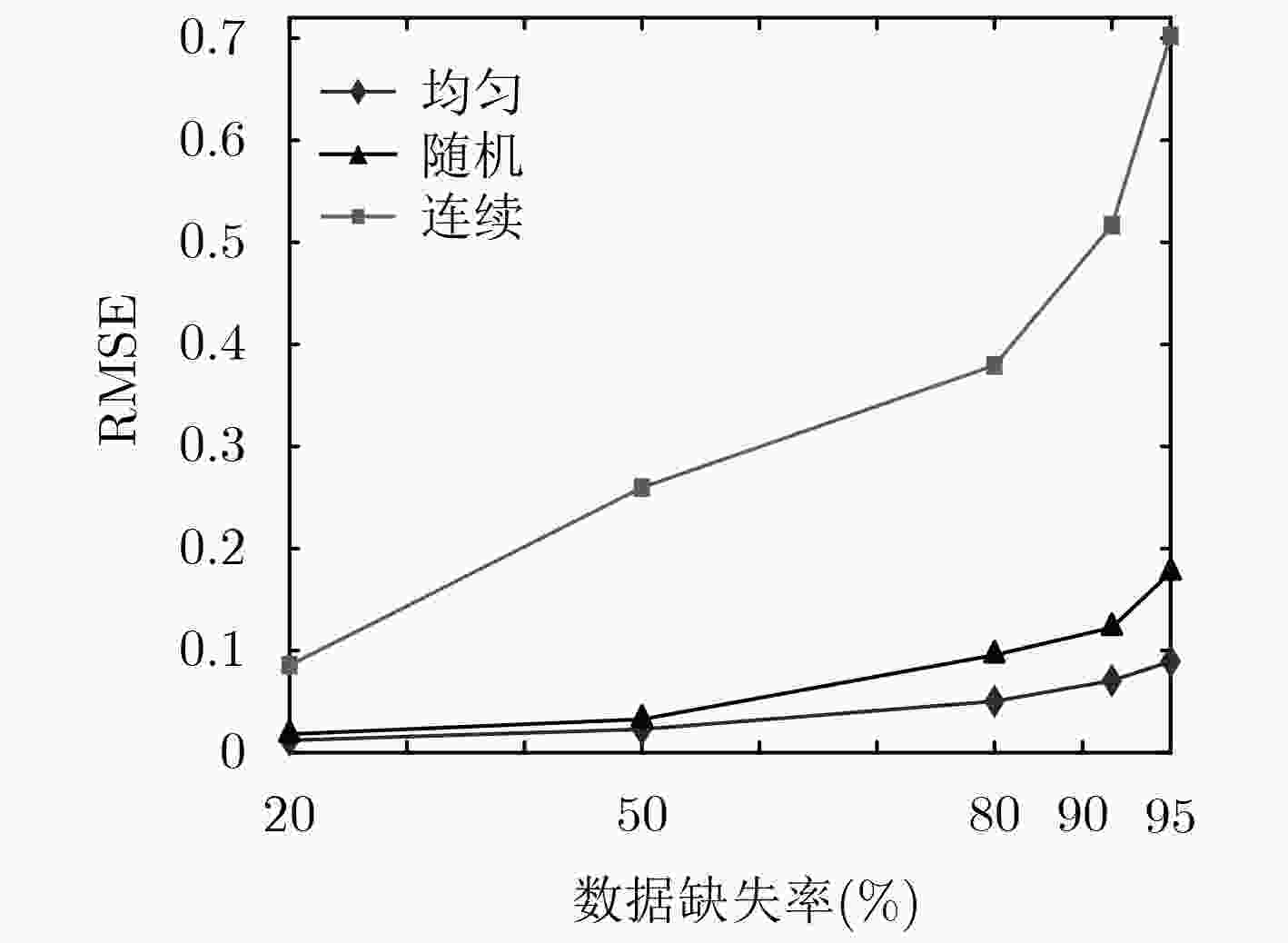
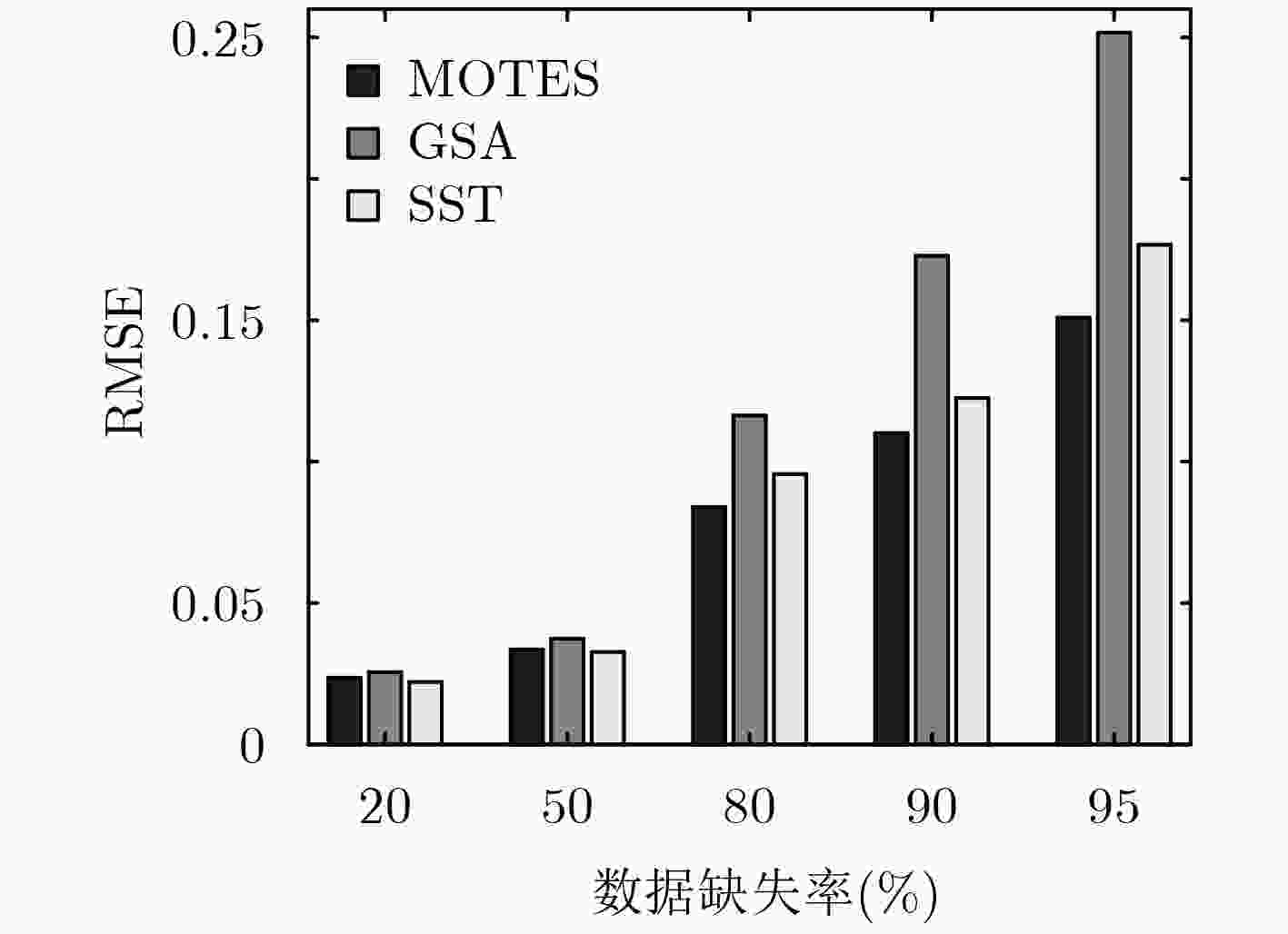
数据缺失率(%) 20 50 80 90 95 MOTES KCS-GAMP-SBL 0.0266 0.0356 0.0840 0.1101 0.1509 TDMF 0.0287 0.0871 0.1962 0.2604 0.3684 SI 0.0862 0.1604 1.0172 1.7662 3.5204 RNN 0.0392 0.0951 0.8875 0.9174 1.0529 KPPCA 0.0278 0.0608 0.1826 0.2769 0.4516 GSA KCS-GAMP-SBL 0.0357 0.0460 0.1985 0.2769 0.3304 TDMF 0.0548 0.1278 0.3557 0.4764 0.5688 SI 0.0935 0.1455 0.8348 2.9442 4.6315 RNN 0.0526 0.0945 1.0858 1.1639 1.7984 KPPCA 0.0498 0.1012 0.3892 0.4879 0.5872 SST KCS-GAMP-SBL 0.0181 0.0327 0.0956 0.1225 0.1767 TDMF 0.0242 0.0544 0.1788 0.2374 0.2961 SI 0.0485 0.0851 0.7451 1.3802 2.0596 RNN 0.0262 0.0488 0.3417 0.5896 1.0421 KPPCA 0.0226 0.0644 0.1736 0.2705 0.2909 表 5 不同算法平均运行时间(ART)的比较(s)
SI RNN KPPCA TDMF KCS-GAMP-SBL MOTES 0.7350 3.1832 11.5781 8.4362 3.0802 GSA 1.5361 7.0320 24.8685 20.4093 15.8633 SST 0.7216 2.5216 10.8683 8.9381 2.9032 表 6 稀疏表示基的选择对算法均方根误差(RMSE)的影响
数据缺失率(%) 20 50 80 90 95 MOTES_1 0.0266 0.0356 0.0930 0.1201 0.1509 MOTES_2 0.0312 0.0422 0.1151 0.1387 0.1954 GSA_1 0.0357 0.0460 0.1985 0.2769 0.3304 GSA_2 0.0412 0.0681 0.2313 0.3343 0.4068 SST_1 0.0181 0.0327 0.0996 0.1275 0.1767 SST_2 0.0199 0.0340 0.1265 0.1534 0.2463 -
SOWMYA R and SUNEETHA K R. Data mining with big data[C]. International Conference on Intelligent Systems and Control, Coimbatore, India, 2017: 246–250. doi: 10.1109/ISCO.2017.7855990. JAQUES N, TAYLOR S, SANO A, et al. Multimodal autoencoder: A deep learning approach to filling in missing sensor data and enabling better mood prediction[C]. International Conference on Affective Computing & Intelligent Interaction, San Antonio, USA, 2017: 202–208. doi: 10.1109/ACII.2017.8273601. BALOUJI E, SALOR Q, and ERMIS M. Exponential smoothing of multiple reference frame components with GPUs for real-time detection of time-varying harmonics and interharmonics of EAF currents[C]. IEEE Industry Applications Society Meeting, Cincinatti, USA, 2017: 1–8. doi: 10.1109/IAS.2017.8101815. KOZERA R and WILKOLAZKA M. Natural spline interpolation and exponential parameterization for length estimation of curves[C]. International Conference of Numerical Analysis & Applied Mathematics, Rhodes, Greece, 2017: 1–140. LAO Wenchao, WANG Ying, CHEN Peng, et al. Time series forecasting via weighted combination of trend and seasonality respectively with linearly declining increments and multiple sine functions[C]. International Joint Conference on Neural Networks, Beijing, China, 2014: 832–837. doi: 10.1109/IJCNN.2014.6889609. LIPPI M, BERTINI M, and FRASCONI P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning[J]. IEEE Transactions on Intelligent, Transportation, System, 2013, 14(2): 871–882 doi: 10.1109/TITS.2013.2247040 STRAUMAN A S, BIANCHI F M, and MIKALSEN K Ø. Classification of postoperative surgical site infections from blood measurements with missing data using recurrent neural networks[C]. International Conference on Biomedical & Health Informatics, Las Vegas, USA, 2018: 307–310. doi: 10.1109/BHI.2018.8333430. LI Li, LI Yuebiao, and LI Zhiheng. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence[J]. Transportation Research Part C, 2013, 34(9): 108–120. LI Yuebiao, LI Zhiheng, LI Li, et al. Comparison on PPCA, KPPCA and MPPCA based missing data imputing for traffic flow[C]. Proceedings of IEEE Conference on Intelligent Transportation System, Wuhan, China, 2013: 1535–1540. SHI Weiwei, ZHU Yongxin, and HUANG Tian. Effective prediction of missing data on apache spark over multivariable time series[J]. IEEE Transactions on Big Data, 2018 doi: 10.1109/TBDATA.2017.2719703 HADI A and WAHIDAH I. Delay estimation using compressive sensing on WSN IEEE 802.15.4[C]. International Conference on Control, Electronics, Renewable Energy and Communications, Bandung, Indonesia, 2017: 192–197. doi: 10.1109/ICCEREC.2016.7814975. DUARTEAND M F and BARANIUK R G. Kronecker compressive sensing[J]. IEEE Transactions on Image Processing, 2012, 21(2): 494–504 doi: 10.1109/TIP.2011.2165289 ZHOU Haifei, TAN Liangsheng, GE Fei, et al. Traffic matrix estimation: Advanced-Tomogravity method based on a precise gravity model[J]. International Journal of Communication Systems, 2015, 28(10): 1709–1728 doi: 10.1002/dac.2787 CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129–159 doi: 10.1137/S003614450037906X TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666 doi: 10.1109/TIT.2007.909108 CHARTRAND R and YIN W. Iteratively reweighted algorithms for compressive sensing[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 2008: 3869–3872. doi: 10.1109/ICASSP.2008.4518498. AL-SHOUKAIRI M, SCHNITER P, and RAO B D. A GAMP based low complexity sparse Bayesian learning algorithm[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 294–308 doi: 10.1109/TSP.2017.2764855 SAMUEL M. Intel lab data[OL]. http://db.csail.mit.edu, 2016. FONOLLOSA J, SHEIK S, HUERTA R, et al. Reservoir computing compensates slow response of chemo sensor arrays exposed to fast varying gas concentrations in continuous monitoring[J]. Sensors & Actuators B Chemical, 2015, 215: 618–629. Tropical Atmosphere Ocean. NOAA/Pacific Marine Environmental Laboratory[OL]. http://www.pmel.noaa.gov/tao/proj_over/proj_over.html, 2016. WU Xiaopei and LIU Mingyan. In-situ soil moisture sensing: Measurement scheduling and estimation using compressive sensing[C]. ACM/IEEE, International Conference on Information Processing in Sensor Networks, Beijing, China, 2012: 1–11. doi: 10.1109/IPSN.2012.6920949. -





 下载:
下载:


 下载:
下载:
