混沌灰狼优化算法训练多层感知器

晏福; 徐建中; 李奉书

doi:10.11999/JEIT180519

混沌灰狼优化算法训练多层感知器

doi: 10.11999/JEIT180519

哈尔滨工程大学经济管理学院哈尔滨 150001

基金项目: 国家社会科学基金(16BJY078)，黑龙江省经济社会发展重点研究课题(KY10900170004)，黑龙江省哲学社会科学研究规划(17JYH49)

详细信息

作者简介:
晏福：男，1989年生，博士生，研究方向为智能优化算法、神经网络和数据挖掘

徐建中：男，1959年生，教授，博士生导师，研究方向为管理科学前沿研究

李奉书：男，1989年生，博士生，研究方向为管理科学前沿研究

通讯作者:
徐建中　xujianzhongxjz@163.com

中图分类号: TP301.6
计量
- 文章访问数: 1914
- HTML全文浏览量: 774
- PDF下载量: 102
- 被引次数: 36
出版历程
- 收稿日期: 2018-05-28
- 修回日期: 2018-12-03
- 网络出版日期: 2018-12-14
- 刊出日期: 2019-04-01

Training Multi-layer Perceptrons Using Chaos Grey Wolf Optimizer

School of Economics and Management, Harbin Engineering University, Harbin 150001, China

Funds: The National Social Science Foundation of China (16BJY078), The Key Program of Economic and Social of Heilongjiang Province (KY10900170004), The Philosophy and Social Science Research Planning Program of Heilongjiang Province (17JYH49)

摘要

摘要:
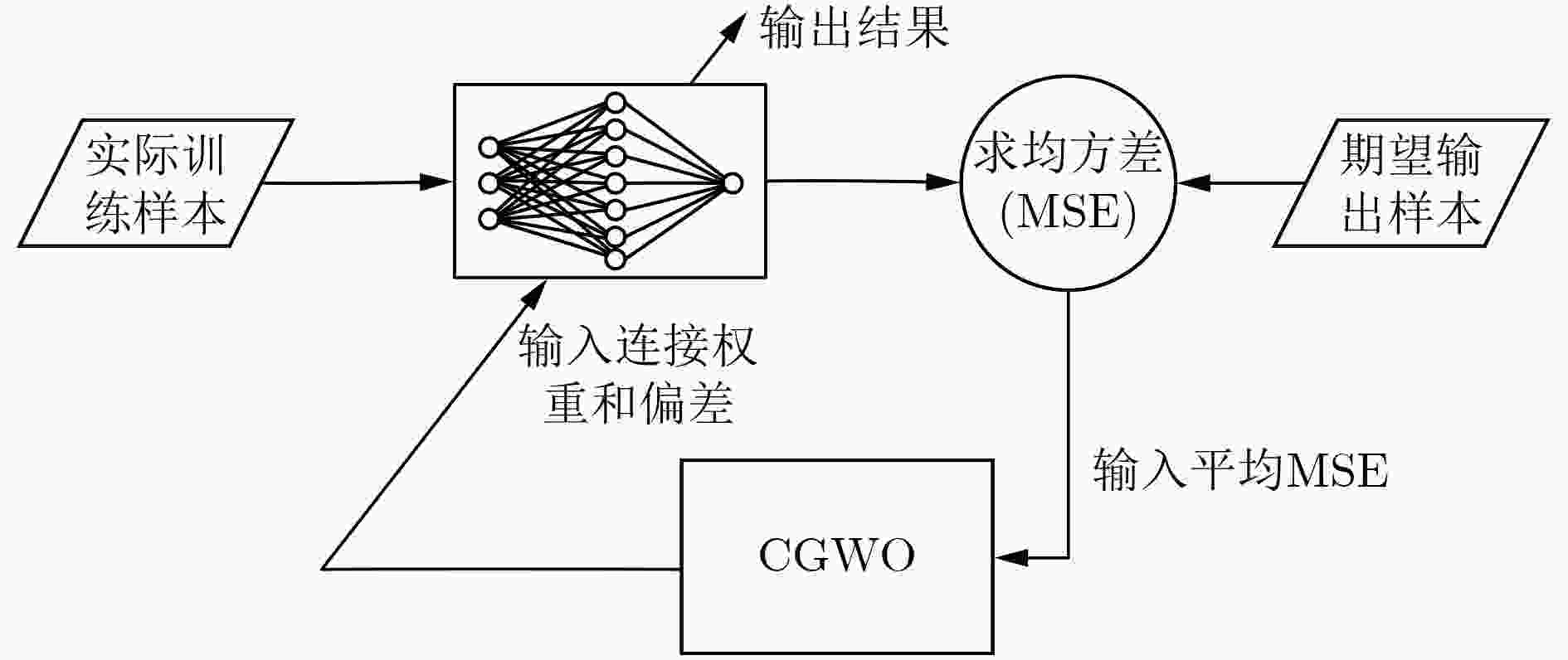
灰狼优化算法(GWO)是一种新的基于灰狼捕食行为的元启发式算法，被证明是一种具有高水平的探索和开发能力的算法。但是存在开发和探索不平衡的问题，以至于其优化性能并不理想。该文将混沌理论引入GWO中，用于平衡GWO的探索和开发，提出一种改进的混沌灰狼优化算法(CGWO)，并应用于多层感知器(MLPs)的训练。首先，基于Cubic混沌理论对GWO的位置更新公式进行改进，以增加个体的多样性，增大跳出局部最优的概率和对解空间进行深入的搜索；其次，设计一种非线性收敛因子，用于协调和平衡CGWO算法在不同迭代进化时期的探索和开发能力；最后，将CGWO算法作为MLPs的训练器，用于对3个复杂分类问题进行分类实验。结果表明：CGWO在分类准确率，避免陷入局部最优，全局收敛速度和鲁棒性方面相较于其他对比算法均具有较好的性能。
- 灰狼优化算法 /
- 混沌理论 /
- 非线性收敛因子 /
- 多层感知器 /
- 分类问题
Abstract:
The Grey Wolf Optimizer (GWO) algorithm mimics the leadership hierarchy and hunting mechanism of grey wolves in nature, and it is an algorithm with high level of exploration and exploitation capability. This algorithm has good performance in searching for the global optimum, but it suffers from unbalance between exploitation and exploration. An improved Chaos Grey Wolf Optimizer called CGWO is proposed, for solving complex classification problem. In the proposed algorithm, Cubic chaos theory is used to modify the position equation of GWO, which strengthens the diversity of individuals in the iterative search process. A novel nonlinear convergence factor is designed to replace the linear convergence factor of GWO, so that it can coordinate the balance of exploration and exploitation in the CGWO algorithm. The CGWO algorithm is used as the trainer of the Multi-Layer Perceptrons (MLPs), and 3 complex classification problems are classified. The statistical results prove the CGWO algorithm is able to provide very competitive results in terms of avoiding local minima, solution precision, converging speed and robustness.
- Grey Wolf Optimizer (GWO) /
- Chaos theory /
- Nonlinear convergence factor /
- Multi-Layer Perceptrons (MLPs) /
- Classification problem

HTML全文

1. 引言

“导航”、“定位”与“授时”(Positioning, Navigation and Timing, PNT)体系构建是中国近些年来最重要的国家战略之一^[1]，而全球导航卫星系统(Global Navigation Satellite System, GNSS)具有全球性、全天候和高精度的特点，成为了国家综合PNT体系中关键的组成部分^[2]。此外，随着信息时代的发展，电力系统、金融系统、通信系统等对授时精度的要求也越来越高，而传统授时方法如网络时间协议(Network Time Protocol, NTP)受到计算能力和存储空间的限制，远距离校准精度不高。因此，基于GNSS的精密授时研究得到了广泛关注^[3,4]。

传统的GNSS精密授时技术是基于伪距单点定位原理，由于伪距观测噪声较大，其精度仅能达到纳秒级。伴随着精密单点定位(Precise Point Positioning, PPP)技术的发展，它在时间传递和授时领域也得到了一定的应用^[5,6]。张小红等人^[7]开展了全球定位系统(Global Positioning System, GPS) PPP时间传递实验，静态实验结果表明时间传递精度在0.1～0.2 ns；同样地，文献[8]计算得到的GPS单系统精密授时精度最高也可达0.1 ns。但是，他们的处理策略仅适用于事后处理，不能实时评估授时精度。针对多系统星座^[9]，文献[10]分析了GPS单系统和GPS + 格洛纳斯(GLObal NAvigation Satellite System, GLONASS)计算的时间传递情况，结果表明两种方案的授时精度类似，即GPS + GLONASS多系统组合方案并没有提高授时精度。电离层延迟也会对授时精度造成影响，文献[11]对比评估了无电离层，经电离层校正和受电离层约束的3种单频精密单点定位(Single Frequency Precise Positioning System, SF-PPP)模型，结果表明电离层约束模型授时精度优于另外两种模型,同时还考虑到了高度角对授时精度的影响。参照消电离层组合模型，闫伟等人^[12]研究了非组合PPP模型在精密授时中的可行性，推测其在运动载体精密授时方面具有较大价值，但是他们仅考虑了静态和静态仿动态两种场景。总之，现有基于GNSS PPP技术的精密授时方法仍存在一些亟需解决的问题：(1)现有PPP技术大部分是基于消电离层组合模型，但是它利用了伪距和载波相位观测值的线性组合，组合噪声较高，从而影响了授时精度；(2)大部分研究是基于GPS，而伴随着北斗三号系统的建设及开通^[13]，信号质量得到极大提升^[14]，基于北斗卫星导航系统(BeiDou navigation Satellite system, BDS)的精密授时研究具有重要意义^[15]；(3)现有研究多是针对静态场景或采用静态模拟动态场景，因此在处理载波相位周跳时多是采用事后处理的方式，且授时精度解算时也采用国际GNSS服务(International GNSS Service, IGS)发布的事后精密星历等，不能满足动态条件下实时解算的要求^[16]。

本文首先介绍了传统消电离层组合PPP模型；其次，针对消电离层组合造成噪声放大的问题，引入了非组合PPP模型，并分别采用Kalman滤波中的静态模型和动态加速模型开展时间传递解算；再次，给出了精密授时精度实时处理策略，并分别对静态场景和车载实时动态场景下的BDS精密授时精度进行了解算，而且与GPS做比较；最后，给出论文的主要结论。

2. 模型介绍

2.1 消电离层组合PPP模型

消电离层组合PPP模型通过将两个不同频率的观测值进行线性组合，消除了载波相位和伪距观测值上的1阶电离层延迟项，只估计接收机坐标、接收机钟差、天顶对流层延迟和模糊度4类参数^[7]

$\begin{split} \quad P_{{\rm{IF}}}^s =& {\rho ^s} + {\rm{c}} \cdot \delta {t^s} - {\rm{c}} \cdot \delta {t_r} + {T^s} \\ &+ {\rm{c}} \cdot {b_{{\rm{IF}}}} + {\rm{c}} \cdot b_{{\rm{IF}}}^s + \varepsilon _{{\rm{IF}},P}^s \end{split}$

(1)

$\begin{split} \quad \phi _{{\rm{IF}}}^s =& {\rho ^s} + {\rm{c}} \cdot \delta {t^s} - {\rm{c}} \cdot \delta {t_r} + {T^s} + {\lambda _{{\rm{IF}}}} \cdot N_{{\rm{IF}}}^s \\ &+ {\lambda _{{\rm{IF}}}} \cdot {B_{{\rm{IF}}}} + {\lambda _{{\rm{IF}}}} \cdot B_{{\rm{IF}}}^s + \varepsilon _{{\rm{IF}},\phi }^s \end{split}$

(2)

其中，下标IF表示消电离层组合； $P_{{\rm{IF}}}^s$ 表示消电离层组合后的伪距观测值，单位为m，且 $P_{{\rm{IF}}}^s = (\mu _i^sP_1^s - P_i^s)/(\mu _i^s - 1)$ , $\mu_{i}^{s}=f_{1}^{2} / f_{i}^{2}, \quad \mu$ 表示电离层放大因子； $f$ 表示频率，单位为Hz，其下标 $i$ 代表不同的频点； $\phi _{{\rm{IF}}}^s$ 表示消电离层组合后的载波相位观测值，单位为m，且 $\phi _{{\rm{IF}}}^s = (\mu _i^s\phi _1^s - \phi _i^s)/(\mu _i^s - 1)$ ; $\rho^{s}$ 表示信号发射时刻的卫星位置到信号接收时刻的接收机位置之间的几何距离，单位为m；c表示真空中的光速； $\delta t^{s}, \delta t_{r}$ 分别表示卫星和接收机钟差，单位为s； $T^{s}$ 表示对流层延迟，单位为m； ${b_{{\rm{IF}}}}$ , $b_{{\rm{IF}}}^s$ 分别表示接收机和卫星硬件延迟误差，单位为s； $\lambda _{{\rm{IF}}}^s$ 表示消电离层组合的组合波长，单位为m； ${B_{{\rm{IF}}}}$ , $B_{{\rm{IF}}}^s$ 分别表示接收机和卫星相位中心偏差，单位为周； $N_{{\rm{IF}}}^s$ 表示载波相位整周模糊度，单位为周； $\varepsilon _{{\rm{IF,}}P}^s$ , $\varepsilon _{{\rm{IF,}}\phi }^s$ 分别表示伪距和载波相位观测值的测量噪声。

由于观测值受到噪声及多路径效应影响较严重的时段主要是在低高度角时，PPP中一般采用分段定权的方法。因此，伪距和载波相位观测值的方差定义为

$\sigma _P^2 = \left\{ \begin{aligned} & {\frac{{\sigma _{P,0}^2}}{{\sin \theta }}{\rm{, }}\;\;\theta > \alpha {\rm{ }}} \\ & {\frac{{\sigma _{P,0}^2}}{{{{\sin }^2}\theta }}{\rm{, }}\;\;\theta \le \alpha {\rm{ }}} \end{aligned} \right.$

(3)

$\sigma _\phi ^2 = \left\{ \begin{aligned} & {\frac{{\sigma _{\phi ,0}^2}}{{\sin \theta }}{\rm{, }}\;\;\theta > \alpha {\rm{ }}} \\ & {\frac{{\sigma _{\phi ,0}^2}}{{{{\sin }^2}\theta }}{\rm{, }}\;\;\theta \le \alpha {\rm{ }}} \end{aligned} \right.$

(4)

其中， $\theta$ 为卫星高度角； $\sigma_{P,0}^{2}, \sigma_{\phi,0}^{2}$ 分别为伪距和载波相位观测值的先验方差； $\alpha$ 为设置的高度角限值，一般取30°。对于BDS和GPS, $\sigma_{P,0}^{2}, \sigma_{\phi,0}^{2}$ 通常分别取0.09 m²和4×10^–6 m^2[17]。

2.2 非组合PPP模型

尽管消电离层组合能够消除电离层1阶项的影响，但是在观测方程式(1)和式(2)中，新的观测值由原始单频点伪距或载波相位观测值组合而来，因此观测噪声会变大。随着PPP技术的发展，研究者们提出了非组合PPP模型，其观测方程为^[12]

$\begin{split} \qquad P_i^s =& {\rho ^s} + {\rm{c}} \cdot \delta {t^s} - {\rm{c}} \cdot \delta {t_r} + {T^s} \\ & + \mu _i^s \cdot {I^s} + {\rm{c}} \cdot {b_i} + {\rm{c}} \cdot b_i^s + \varepsilon _{i,P}^s \end{split}$

(5)

$\begin{split} \qquad \phi _i^s = &{\rho ^s} + {\rm{c}} \cdot \delta {t^s} - {\rm{c}} \cdot \delta {t_r} + {T^s} - {I^s} \\ &+ \lambda _i^s \cdot N_i^s + \lambda _i^s \cdot {B_i} + \lambda _i^s \cdot B_i^s + \varepsilon _{i,\phi }^s \end{split}$

(6)

其中， ${I^s}$ 表示卫星 $s$ 在信号传播路径上的电离层延迟，单位为m。其他各个变量的含义与式(1)、式(2)中类似，不同之处在于式(5)和式(6)中变量仅代表单个频点。

非组合PPP模型增加了电离层参数，其余噪声方差与消电离层组合PPP类似。假设各个频点下的伪距、载波相位观测值相互独立，那么单历元观测值的随机模型为

${\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{P,1}^2}&{}&{}&{}&{}&{} \\ {}& \ddots &{}&{}&{}&{} \\ {}&{}&{\sigma _{P,m}^2}&{}&{}&{} \\ {}&{}&{}&{\sigma _{\phi ,1}^2}&{}&{} \\ {}&{}&{}&{}& \ddots &{} \\ {}&{}&{}&{}&{}&{\sigma _{\phi ,m}^2} \end{array}} \right]$

(7)

在非组合PPP中，电离层延迟项被当作未知参数进行估计，它通常被描述为1阶高斯马尔科夫随机过程，即

${Q_{{\rm{ion}}}}{\rm{ = }}\left[ {{q_{{\rm{ion}}}}\Delta t} \right]$

(8)

其中， ${Q_{{\rm{ion}}}}$ 表示电离层延迟的谱密度； $\Delta t$ 表示两个相邻历元的时间间隔。

不同于消电离层组合，非组合PPP模型中的原始噪声不会被放大，但相应地，它增加了电离层延迟等未知参数，计算复杂度也更高。尽管BDS与GPS的非组合PPP模型是一致的，但是两种系统本身具有不同的特点——信号体制、轨道类型和星座构型等均不相同，因此开展BDS精密授时研究是必要的。

2.3 参数估计

在非组合PPP定位解算时，Kalman滤波不需要保留前面的数据，只需要上一个历元的状态和当前历元的观测值就可以递推出新的状态估值。Kalman滤波的状态模型和观测模型为

$\left. \begin{split} & {{\boldsymbol{X}}_k} = {{\boldsymbol{F}}_{k,k - 1}}{{\boldsymbol{X}}_{k - 1}} + {{\boldsymbol{w}}_{k - 1}}{\rm{ }}{{\boldsymbol{w}}_{k - 1}} \sim N(0,{{\boldsymbol{Q}}_{k - 1}}) \\ & {{\boldsymbol{L}}_k} = {{\boldsymbol{H}}_k}{{\boldsymbol{X}}_k} + {{\boldsymbol{n}}_k}{\rm{ }}{{\boldsymbol{n}}_k}\sim N(0,{{\boldsymbol{R}}_k}) \end{split}\right\}$

(9)

其中， $k$ 表示观测历元时刻； ${{\boldsymbol{X}}_k}$ 表示状态向量，由于对流层延迟干分量可以通过模型改正，因此它表示为

$\begin{split} {{\boldsymbol{X}}_k} =& [X \ \ Y \ \ Z \ \ {V_x} \ \ {V_y} \ \ {V_z} \ \ {a_x}\ \ {a_y} \ \ {a_z} \ \ \delta {t_r} \\ & {{\boldsymbol{I}}_{(1 \times m)}} \ \ {\boldsymbol{T}}_{(1 \times m)}^{\rm{w}} \ \ {N^1} \ \ \cdots \ \ {N^m}{]^{\rm{T}}} \end{split}$

(10)

且 ${\boldsymbol{I}}$ 表示不同卫星在信号传播路径上的电离层延迟， ${{\boldsymbol{T}}^{\rm{w}}}$ 表示不同卫星在天顶方向上的对流层延迟湿分量； $\boldsymbol{w}_{k-1}$ 和 $\boldsymbol{Q}_{k-1}$ 分别为动态噪声矩阵及其协方差阵； $\boldsymbol{n}_{k}$ 和 $\boldsymbol{R}_{k}$ 分别为观测噪声向量及其协方差阵； $\boldsymbol{L}_{k}$ 表示观测向量，为

${{\boldsymbol{L}}_k} = \left[ {{P^1}}\ \ {{P^2}}\ \ \cdots \ \ {{P^m}}\ \ {{\phi ^1}}\ \ {{\phi ^2}} \ \ \cdots \ \ {{\phi ^m}} \right]^{\rm{T}}$

(11)

$\boldsymbol{F}_{k, k-1}$ 表示状态转移矩阵， $\boldsymbol{H}_{k}$ 为系数矩阵，它们分别为

${\boldsymbol{F}}_{k,k-1}=\left[\begin{array}{ccccc}{\boldsymbol{F}}_{{\rm{pos}}}& 0& \cdots & \cdots & 0\\ 0& {\boldsymbol{F}}_{{\rm{clk}}}& \ddots & ⋮& ⋮\\ ⋮& \ddots & {\boldsymbol{F}}_{{\rm{Ion}}}& \ddots & ⋮\\ ⋮& ⋮& \ddots & {\boldsymbol{F}}_{{\rm{trop}}}& 0\\ 0& \cdots & \cdots & 0& {\boldsymbol{F}}_{N}\end{array}\right]$

(12)

${{\boldsymbol{H}}_k} = \left[ {\begin{array}{*{20}{c}} {{a^1}}&{{b^1}}&{{c^1}}&0&0&0&0&0&0&{ - c}&{{\boldsymbol{d}}_{(1 \times m)}^1}&{{\boldsymbol{e}}_{(1 \times m)}^1}&0& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{a^m}}&{{b^m}}&{{c^m}}&0&0&0&0&0&0&{ - c}&{{\boldsymbol{d}}_{(1 \times m)}^m}&{{\boldsymbol{e}}_{(1 \times m)}^m}&0& \cdots &0 \\ {{a^1}}&{{b^1}}&{{c^1}}&0&0&0&0&0&0&{ - c}&{ - {\boldsymbol{d}}_{(1 \times m)}^1}&{{\boldsymbol{e}}_{(1 \times m)}^1}&{{\lambda ^1}}& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &{ - c}& \vdots & \vdots & \vdots & \ddots & \vdots \\ {{a^m}}&{{b^m}}&{{c^m}}&0&0&0&0&0&0&{ - c}&{ - {\boldsymbol{d}}_{(1 \times m)}^m}&{{\boldsymbol{e}}_{(1 \times m)}^m}&0& \cdots &{{\lambda ^m}} \end{array}} \right]$

(13)

其中， ${\boldsymbol{d}}_{(1 \times m)}^i$ 表示第 $i$ 个元素为1，其余为0； ${\boldsymbol{e}}_{(1 \times m)}^i$ 表示第 $i$ 个元素为投影函数NMF，其余为0。

Kalman滤波分为预测和更新两个过程，其中预测部分基于上一个历元的估计值及状态转移矩阵推导下一个历元的状态向量；更新部分再根据当前历元的观测值，对预测部分得到的状态向量进行更新^[18]。Kalman滤波常用的运动模型有如下3种：(1)静态模型，即接收机静止不动，速度为0；(2)匀速运动模型，接收机载体做匀速运动，速度为恒定值，加速度为0；(3)动态加速模型，接收机载体做加速度变化的变速运动。其中，在静态模型中， ${{\boldsymbol{F}}_{{\rm{pos}}}}$ 为9×9单位矩阵；在匀速运动模型，它为

${{\boldsymbol{F}}_{{\rm{pos}}}} = {\left[ {\begin{array}{*{20}{c}} 1&0&0&{\Delta t}&0&0&0&0&0 \\ 0&1&0&0&{\Delta t}&0&0&0&0 \\ 0&0&1&0&0&{\Delta t}&0&0&0 \\ 0&0&0&1&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&0&1 \end{array}} \right]_{(9 \times 9)}}$

(14)

而在动态加速模型中，它为

$\begin{split} & {{\boldsymbol{F}}_{{\rm{pos}}}} =\\ & {\left[ {\begin{array}{*{20}{c}} 1 & 0 & 0 & {\Delta t} & 0 & 0 & {\Delta {t^2}/2} & 0 & 0 \\ 0 & 1 & 0 & 0 & {\Delta t} & 0 & 0 & {\Delta {t^2}/2} & 0 \\ 0 & 0 & 1 & 0 & 0 & {\Delta t} & 0 & 0 & {\Delta {t^2}/2} \\ 0 & 0 & 0 & 1 & 0 & 0 & {\Delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & {\Delta t} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & {\Delta t} \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}} \right]_{(9 \times 9)}} \end{split}$

(15)

根据后文实验场景的实际情况，本文采用静态模型和动态加速模型进行相关分析。

3. 静态PPP精密授时实验研究

3.1 数据采集与处理策略

本节首先对BDS静态PPP精密授时精度开展研究，并与GPS进行比较。为此，本节选取了2019年10月1日6个IGS测站的双频观测数据，分别研究了静态条件下消电离层组合和非组合PPP模型的授时精度。其中，6个外接原子钟的测站分别为GMSD, KARR, KZN2, MAYG, URUM和WUH2，数据采样间隔为30 s。所选监测站的基本信息列在了表1中。

表 1 静态实验所用IGS监测站的基本信息

监测站	位置	接收机类型	天线类型
GMSD	日本	TRIMBLE NETR9	TRM59800.00
KARR	澳大利亚	TRIMBLE NETR9	TRM59800.00
KZN2	俄罗斯	TRIMBLE ALLOY	TRM59800.00
MAYG	法国	TRIMBLE NETR9	TRM59800.00
URUM	中国	JAVAD TRE_3	JAVRINGANT
WUH2	中国	JAVAD TRE_3	JAVRINGANT

下载: 导出CSV

| 显示表格

本文以IGS精密钟差文件中的监测站钟差作为真值，分析不同PPP模型解算出的接收机钟差精度。静态实验采用的数据采样间隔为30 s，而IGS精密钟差间隔为5 min，因此，本文将每5 min解算得到的钟差与精密钟差进行对比。消电离层组合PPP模型的处理策略见表2，且在参数估计时以单点定位(Single Point Positioning, SPP)的结果作为初始值。两种模型均使用双频原始观测数据。两个频点分别是BDS B1^[19], B3和GPS L1, L2。Kalman滤波过程中噪声、方差或协方差的选择通常是基于经验的，比如当电离层活跃时，方差赋较大值；当电离层稳定时，方差赋较小值。基于选取的静态数据，本文选择的量测噪声、过程噪声和估计误差方差的初值也列在了表2。此外，非组合PPP模型还需要增加电离层延迟项，其初始值设置为0 m，初始标准差设置为1×10² m，电离层延迟过程噪声为1×10^–2。

表 2 静态消电离层组合PPP模型处理策略

误差项	处理策略
卫星星历	IGS提供的精密星历
卫星钟差	IGS提供的精密钟差
对流层延迟	Saastamoinen模型改正干分量，估计湿分量
电离层延迟	消电离层组合
卫星天线相位中心改正	IGS提供的PCO, PCV产品
接收机天线相位中心改正	IGS提供的PCV产品
相位缠绕	模型改正
相对论效应	模型改正
地球自转	模型改正
参数估计与质量控制	处理策略
参数估计	(1)接收机坐标，SPP结果作为初始值，初始标准差为1000 m (2)接收机钟差，SPP结果作为初始值，初始标准差为1000 m (3)天顶对流层湿分量，初始值0.5 m，初始标准差0.01 m (4)模糊度初始值为 $\phi _{{\rm{IF}}}^s - P_{{\rm{IF}}}^s$ ，标准差为1000 m
数据质量控制	标准卡尔曼滤波
观测值随机模型	高度角定权

下载: 导出CSV

| 显示表格

3.2 静态PPP精密授时结果与分析

PPP中位置估值的精度会影响钟差参数估计的精度。因此，为评估静态非组合PPP位置解算精度，本节将其解算出的位置坐标与IGS提供的监测站参考坐标作差。各测站E, N, U方向上位置估值差值的均方根(Root Mean Square, RMS)值和标准差(STandard Deviation, STD)分别见表3和表4^[20]。

表 3 BDS/GPS各测站E, N, U方向RMS值(m)

监测站	BDS			GPS
监测站	E	N	U	E	N	U
GMSD	0.008	0.006	0.021	0.007	0.008	0.040
KARR	0.021	0.003	0.016	0.032	0.007	0.011
KZN2	0.016	0.004	0.043	0.008	0.006	0.021
MAYG	0.012	0.019	0.053	0.007	0.004	0.035
URUM	0.016	0.019	0.015	0.014	0.005	0.027
WUH2	0.017	0.009	0.049	0.015	0.011	0.045

下载: 导出CSV

| 显示表格

表 4 BDS/GPS各测站E, N, U方向的STD(m)

监测站	BDS			GPS
监测站	E	N	U	E	N	U
GMSD	0.006	0.005	0.015	0.004	0.004	0.001
KARR	0.010	0003	0.009	0.013	0.003	0.015
KZN2	0.003	0.002	0.006	0.008	0.003	0.004
MAYG	0.007	0.003	0.037	0.006	0.003	0.018
URUM	0.003	0.005	0.012	0.011	0.002	0.012
WUH2	0.009	0.003	0.041	0.009	0.002	0.016

下载: 导出CSV

| 显示表格

由表3、表4可以看出，收敛后各测站E, N, U各方向RMS值分别在0.02 m, 0.01 m, 0.04 m左右。各测站E方向的STD均在1 cm以内，N方向的STD在5 mm以内，只有U方向的STD最高可达4 cm。这都表明静态非组合PPP模型解算结果内符合精度高。由此可知，BDS和GPS定位精度相当，在亚太地区尤其是在中国境内，BDS的定位精度要高于GPS。

接下来分别采用消电离层组合PPP(经典PPP)和非组合PPP模型解算接收机钟差，并和IGS提供的精密钟差文件对比，得到各测站接收机的钟差误差如图1所示，其中消电离层组合的参数估计参照朱荷欢等人的方法^[8]，静态条件下的载波相位模糊度采用固定解。由于IGS提供的监测站精密钟差产品是基于GPS时间系统的，因此BDS解算出的钟差与IGS提供的精密钟差存在系统误差。考虑到系统误差后，表5只给出了GPS静态PPP钟差误差的RMS值，而不同PPP模型计算出BDS, GPS的钟差误差的STD见表6。

图 1 BDS/GPS中经典PPP、非组合PPP模型解算的钟差误差

下载: 全尺寸图片幻灯片

表 5 GPS静态PPP钟差误差的RMS值(ns)

监测站	GPS
监测站	消电离层组合PPP	非组合PPP
GMSD	0.257	0.187
KARR	0.245	0.147
KZN2	0.231	0.161
MAYG	0.323	0.258
URUM	0.186	0.222
WUH2	0.278	0.187

下载: 导出CSV

| 显示表格

表 6 BDS/GPS静态PPP钟差解误差的STD(ns)

监测站	BDS		GPS
监测站	消电离层组合	非组合	消电离层组合	非组合
GMSD	0.181	0.183	0.246	0.174
KARR	0.089	0.070	0.197	0.147
KZN2	0.203	0.131	0.167	0.150
MAYG	0.217	0.150	0.318	0.171
URUM	0.124	0.075	0.198	0.112
WUH2	0.103	0.148	0.205	0.103

下载: 导出CSV

| 显示表格

由图1、表5和表6可知，对GPS而言，消电离层组合PPP算法和非组合PPP算法的RMS值分别在0.33 ns, 0.26 ns以内，同样非组合PPP算法钟差解误差的STD优于消电离层组合PPP算法，分别在0.18 ns和0.32 ns以内；对BDS而言，消电离层组合PPP算法和非组合PPP算法钟差解误差的STD分别在0.22 ns和0.19 ns以内：这说明静态条件下GPS和BDS非组合PPP算法精度高于消电离层组合PPP算法。对比BDS, GPS，加之考虑到BDS与GPS定位精度相当，在亚太地区定位精度甚至高于GPS，因此断定BDS静态精密授时精度略高于GPS；对比两种PPP算法，消电离层组合PPP和非组合PPP解出的钟差误差大部分相差在0.1 ns以内，但非组合PPP算法的精密授时精度优于消电离层组合PPP算法。但是从图1还发现在某些时段内，KZN2, WUH2中两种PPP模型解算出的钟差存在较大差别，下面逐个对其开展分析。

KZN2, WUH2在观测期间的卫星数量和空间位置精度因子(Position Dilution Of Precision, PDOP)如图2所示。结合图1，从KZN2钟差解算结果可知，某些时间段BDS两种PPP模型解算出的钟差出现了较大的非系统性偏差，而从图2可知，在06:00～08:00, 16:00, 20:00左右的时间段，BDS有效卫星数发生变化，PDOP突然增大。因此，本文认为这是造成两种PPP模型解算出的钟差差别较大的原因。

图 2 KZN2, WUH2在观测期间的卫星数量(NSAT)和PDOP

下载: 全尺寸图片幻灯片

WUH2站位于我国中部的武汉市，该站观测到的BDS导航卫星数量最高可达17颗，远高于观测到的GPS导航卫星。因此，结合图1和图2，BDS的PDOP普遍低于GPS，且BDS解算的钟差误差大部分在0.3 ns以内。对WUH2而言，BDS两种PPP算法和GPS消电离层组合PPP算法的钟差误差在某些时间段也都出现了较大的起伏，尤其是在10:00, 12:00, 14:00, 16:00以及20:00前后。对应图2可知，这些时段BDS的PDOP均出现突变，进而导致相应的钟差解算误差增加。同样地，GPS 04:00～08:00之间和16:00左右，钟差误差也出现了相似情况。

4. 动态PPP精密授时实验研究

4.1 数据采集与处理策略

当前精密授时精度的相关研究多是集中在静态条件下，动态分析多是采用静态模拟动态来实现。因此，为了更完备地分析PPP在动态情况下的精密授时精度，本节开展了车载动态实验研究。实验开展于UTC时间2019年5月16日，全程约50 km，总时长约3 h 30 min，共采集到约12900个历元时刻的数据。实验采用Novatel接收机，采样间隔为1 s，卫星截止高度角设置为10°。考虑到实时性要求，本节基于超快速预报星历对车载数据进行PPP钟差解算，参数估计和处理策略如表7所示，天线相位偏差采用Igs14.atx修正，其他与静态PPP相同。对于载波相位模糊度，当汽车加减速或信号被遮挡时采用浮点解，其他情况下采用固定解。同时，本文选择的量测噪声、过程噪声和估计误差方差的初值也列在了表7。其余参数与第3节相同。

表 7 动态PPP中参数估计处理策略

参数估计	处理策略
接收机坐标	SPP结果作为初始值，初始标准差为100 m
接收机速度	原始多普勒解为初始值，初始标准差5 m/s，动态噪声为10 m/s
接收机加速度	初始值为1×10^–6 m/s²，初始标准差为5 m/s²，动态噪声为1×10^–2 m/s²
接收机钟差	SPP结果作为初始值，初始标准差为1000 m
天顶对流层湿分量	初始值0.5 m，初始标准差为0.01 m
模糊度	初始值为 $\phi _{{\rm{IF}}}^s - P_{{\rm{IF}}}^s$ ，标准差为1000 m

下载: 导出CSV

| 显示表格

4.2 动态PPP精密授时结果与分析

车载实验中接收机没有外接原子钟，加之考虑到PPP事后双向滤波解的精度高于实时动态PPP解，因此本节把事后PPP双向滤波解算的钟差作为接收机钟差的“真值”，来分析实时动态PPP的授时精度。动态PPP钟差误差的RMS, STD和均值见表8。

表 8 动态PPP钟差误差RMS, STD和均值(ns)

评估指标	GPS		BDS
评估指标	非组合	消电离层组合	非组合	消电离层组合
RMS	1.154	1.880	1.244	2.088
STD	1.079	1.309	1.237	2.079
均值	–0.409	–1.349	0.135	–0.193

下载: 导出CSV

| 显示表格

由表可知，BDS和GPS采用预报星历时实时动态PPP钟差解算精度在2 ns以内；GPS授时精度略高于BDS，非组合PPP算法精密授时精度高于消电离层组合PPP算法。而且非组合PPP算法钟差解更平稳、可靠。

为了进一步分析动态PPP算法精密授时的精度以及影响钟差解算的原因，接下来本节对BDS, GPS解算时的卫星数量、PDOP、接收机钟差精度因子(Time Dilution Of Precision, TDOP)以及解算的车辆速度进行统计，分析影响钟差解算精度的原因。BDS, GPS解算中有效卫星数量、PDOP值、TDOP值以及车辆在平面的运行速度和钟差项中误差如图3、图4所示。

图 3 BDS,GPS有效卫星数量(NSAT), PDOP, TDOP及解算的车辆运行速度

下载: 全尺寸图片幻灯片

图 4 BDS, GPS不同PPP模型解算出的钟差误差与钟差项中误差

下载: 全尺寸图片幻灯片

从图3和图4知，对于BDS单系统，实验过程中的大部分时间可以观测到8～10颗BDS导航卫星；PDOP值大部分时间小于3；车辆最高速度为14 m/s，最低速度为0 m/s。对于GPS单系统，实验过程中的大部分时间可以观测到8～10颗GPS导航卫星，最多12颗，其中在02:50～03:40时段，可用卫星数减少到8颗以下；PDOP值大部分时间小于2.5。对比不同历元时钟差项中误差及相应的车辆速度、卫星数量可知，当车辆突然加速、减速，或者道路开阔性不好时，会出现卫星失锁的情况，导致观测值变少以及模糊度重收敛，进而影响到授时精度。对于非组合PPP模型，钟差误差均在2 ns以内，完成收敛后，BDS和GPS钟差项中误差分别小于0.4 m和0.3 m。消电离层组合PPP模型重收敛速度低于非组合模型，但是由于观测值组合放大了噪声，总体上钟差项中误差大于非组合PPP模型，且钟差误差大于非组合PPP模型的钟差误差。对比BDS和GPS两个系统钟差解算精度，由于GPS卫星数量相对稳定，不易失锁从而不需频繁重收敛，因此GPS钟差解算精度要高于BDS。但当两个系统在完成收敛且不发生重收敛的情况下，BDS和GPS钟差解算精度相当，钟差项中误差均在0.3 m以内。非组合PPP模型由于使用原始观测数据，避免了数据组合带来的噪声放大，因而精密授时精度高于消电离层组合PPP模型。总之，非组合PPP算法比消电离层组合PPP算法更平滑、稳定，其钟差解同事后PPP双向滤波解算的钟差结果更吻合。

5. 结束语

针对现有精密授时研究中消电离层组合PPP模型的组合噪声大、卫星导航系统单一和实时动态场景少的问题，本文基于非组合PPP模型对BDS静态和实时动态场景下的精密授时精度开展了研究，主要结论如下：

(1) 静态条件下，BDS和GPS定位精度相当，在亚太地区尤其是在中国境内，BDS的定位精度要高于GPS，因此BDS的精密授时精度更优；消电离层组合PPP模型和非组合PPP模型计算得到的钟差误差大部分相差在0.1 ns以内，但非组合PPP模型的精密授时精度更优。

(2) 实时动态条件下，基于超快速预报星历的BDS和GPS授时精度均在2 ns以内，且GPS更优，但当两种系统均完成收敛且不发生重收敛时，它们的精密授时精度相当；同样地，非组合PPP模型的精密授时精度更优。

(3) PDOP是影响精密授时精度的重要指标；动态条件下，载体速度的突然变化及周围环境的开阔性均可能会造成卫星失锁，致使有效观测值减少及重收敛，进而影响精密授时精度。

图 1 基于CGWO的多层感知器

下载: 全尺寸图片幻灯片

图 2 5种算法对3 bit XOR问题10次独立运行的收敛曲线和分类准确率

下载: 全尺寸图片幻灯片

图 3 5种算法对气球分类问题10次独立运行的收敛曲线和分类准确率

下载: 全尺寸图片幻灯片

图 4 5种算法对虹膜分类问题10次独立运行的收敛曲线和分类准确率

下载: 全尺寸图片幻灯片

表 1 3位奇偶校验问题(3 bit XOR)

输入	输出
0　0　0	0
0　0　1	1
0　1　0	1
0　1　1	0
1　0　0	1
1　0　1	0
1　1　0	0
1　1　1	1

下载: 导出CSV

表 2 5种算法对3 bit XOR问题10次独立运行结果的比较

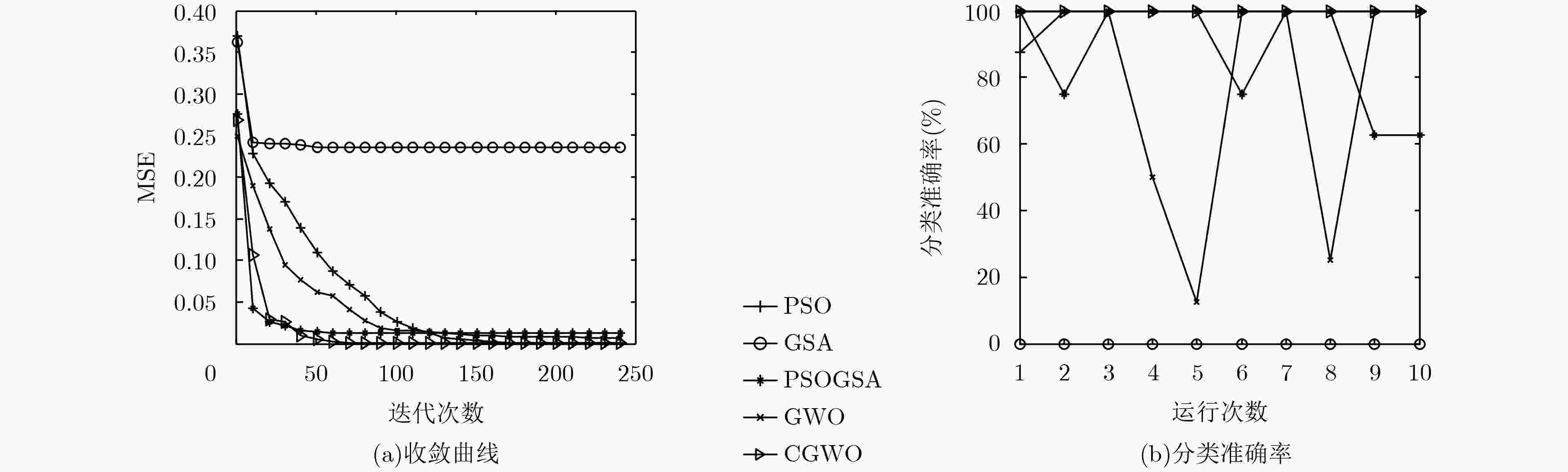
算法	平均值	中值	标准差	最好值
PSO-MLP	1.48e–04	1.65e–05	2.40e–04	7.67e–09
GSA-MLP	2.35e–01	2.38e–01	1.17e–02	2.10e–01
PSOGSA-MLP	1.27e–02	9.29e–06	2.57e–02	1.64e–09
GWO-MLP	7.00e–03	6.07e–03	1.89e–02	2.90e–05
CGWO-MLP	6.01e–06	1.21e–08	1.33e–05	2.69e–09

下载: 导出CSV

表 3 5种算法对气球分类问题10次独立运行结果的比较

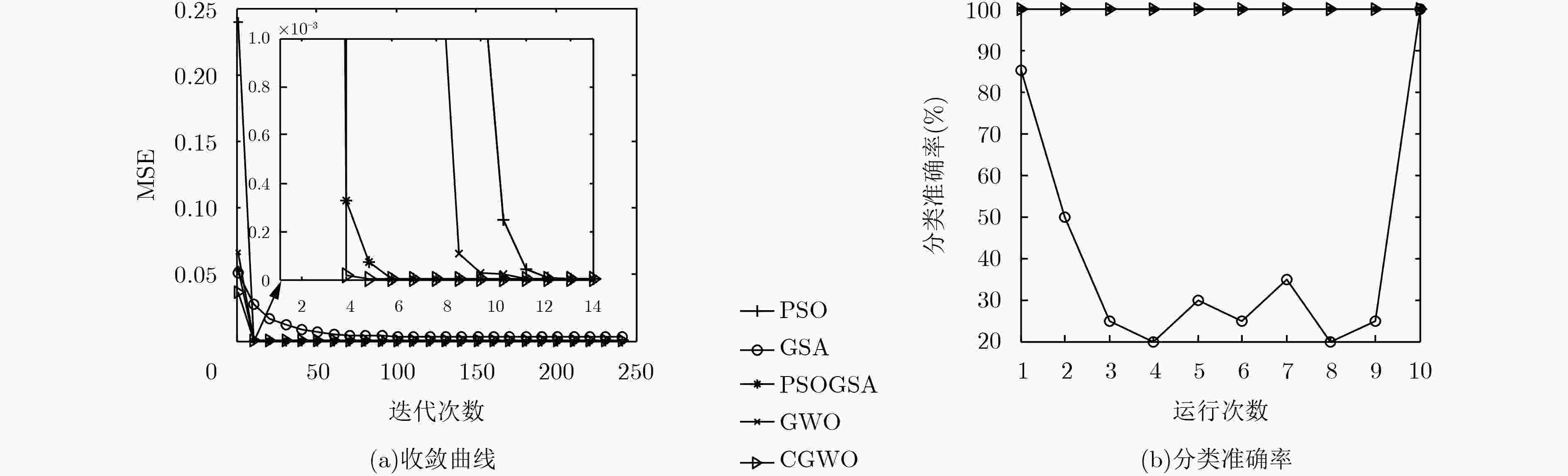
算法	平均值	中值	标准差	最好值
PSO-MLP	0	0	0	0
GSA-MLP	5.90e–03	4.10e–03	6.00e–03	4.69e–04
PSOGSA-MLP	9.85e–32	9.73e–40	2.94e–31	3.81e–61
GWO-MLP	1.12e–18	3.56e–20	2.38e–18	2.49e–26
CGWO-MLP	2.35e–15	2.07e–18	5.03e–15	1.00e–18

下载: 导出CSV

表 4 5种算法对虹膜分类问题10次独立运行结果的比较

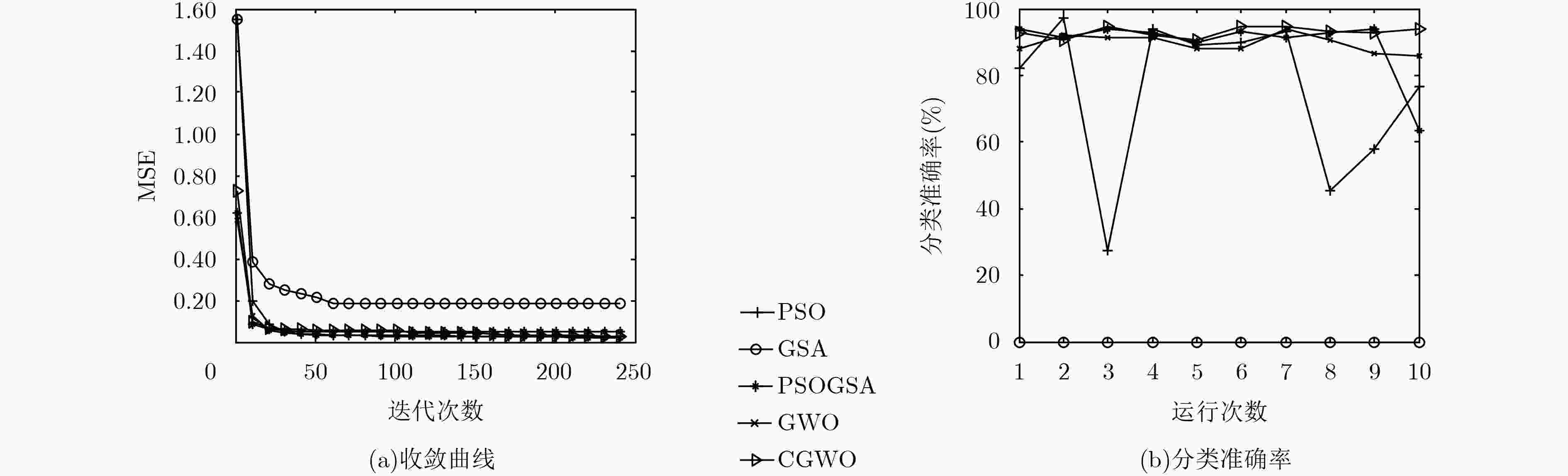
算法	平均值	中值	标准差	最好值
PSO-MLP	2.70e–02	2.47e–02	1.76e–02	6.20e–03
GSA-MLP	1.83e–01	1.89e–01	2.30e–02	1.48e–01
PSOGSA-MLP	4.91e–02	1.84e–02	1.01e–01	1.16e–02
GWO-MLP	2.27e–02	2.19e–02	2.70e–03	1.71e–02
CGWO-MLP	1.90e–02	1.82e–02	4.10e–03	1.39e–02

下载: 导出CSV

参考文献(28)

MCCULLOCH W S and PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. The Bulletin of Mathematical Biophysics, 1943, 5(4): 115–133 doi: 10.1007/BF02478259

BEBIS G and GEORGIOPOULOS M. Feed-forward neural networks[J]. IEEE Potentials, 1994, 13(4): 27–31 doi: 10.1109/45.329294

KOHONEN T. The self-organizing map[J]. Proceedings of the IEEE, 1990, 78(9): 1464–1480 doi: 10.1109/5.58325

JAFRASTEH B and FATHIANPOUR N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation[J]. Neurocomputing, 2017, 235: 217–227 doi: 10.1016/j.neucom.2017.01.016

CHICEA D. Using neural networks for dynamic light scattering time series processing[J]. Measurement Science and Technology, 2017, 28(5): 055206 doi: 10.1088/1361-6501/aa61b4

MORRO A, CANALS V, OLIVER A, et al. A stochastic spiking neural network for virtual screening[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(4): 1371–1375 doi: 10.1109/TNNLS.2017.2657601

MIRJALILI S. How effective is the Grey Wolf Optimizer in training multi-layer perceptrons[J]. Applied Intelligence, 2015, 43(1): 150–161 doi: 10.1007/s10489-014-0645-7

ISA N A M and MAMAT W M F W. Clustered-hybrid multilayer perceptron network for pattern recognition application[J]. Applied Soft Computing, 2011, 11(1): 1457–1466 doi: 10.1016/j.asoc.2010.04.017

韦岗, 李华, 徐秉铮. 关于前馈多层神经网络多维函数逼近能力的一个定理[J]. 电子科学学刊, 1997, 20(4): 433–438

WEI Gang, LI Hua, and XU Bingzheng. A novel theorem on the multi-dimensional function approximation ability of feed forward multi-layer neural networks[J]. Journal of Electronics, 1997, 20(4): 433–438

LIBANO F, RECH P, TAMBARA L, et al. On the reliability of linear regression and pattern recognition feedforward artificial neural networks in FPGAs[J]. IEEE Transactions on Nuclear Science, 2018, 65(1): 288–295 doi: 10.1109/TNS.2017.2784367

LI Feng, ZURADA J M, LIU Yan, et al. Input layer regularization of multilayer feedforward neural networks[J]. IEEE Access, 2017, 5: 10979–10985 doi: 10.1109/ACCESS.2017.2713389

MIRJALILI S, MOHD H S, and MORADIAN S H. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm[J]. Applied Mathematics and Computation, 2012, 218(22): 11125–11137 doi: 10.1016/j.amc.2012.04.069

张长利, 房俊龙, 潘伟. 用遗传算法训练的多层前馈神经网络对番茄成熟度进行自动检测的研究[J]. 农业工程学报, 2001, 17(3): 153–156 doi: 10.3321/j.issn:1002-6819.2001.03.037

ZHANG Changli, FANG Junlong, and PANG Wei. Automated identification of tomato maturation using multilayer feedforward neural network with genetic algorithms (GA)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2001, 17(3): 153–156 doi: 10.3321/j.issn:1002-6819.2001.03.037

ZHANG Ridong and TAO Jili. A nonlinear fuzzy neural network modeling approach using an improved genetic algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5882–5892 doi: 10.1109/TIE.2017.2777415

海宇娇, 刘青昆. 基于差分进化的ELM加权集成分类[J]. 计算机工程与应用, 2017, 53(8): 57–60 doi: 10.3778/j.issn.1002-8331.1510-0051

HAI Yujiao and LIU Qingkun. ELM weighting ensemble classification based on differential evolution[J]. Computer Engineering and Applications, 2017, 53(8): 57–60 doi: 10.3778/j.issn.1002-8331.1510-0051

LEEMAA N, NEHEMIAHA H K, and KANNANB A. Neural network classifier optimization using differential evolution with global information and back propagation algorithm for clinical datasets[J]. Applied Soft Computing, 2016, 49: 834–844 doi: 10.1016/j.asoc.2016.08.001

MICHALIS M and YANG Shengxiang. Training neural networks with ant colony optimization algorithms for pattern classification[J]. Soft Computing, 2015, 19(6): 1511–1522 doi: 10.1007/s00500-014-1334-5

KRZYSZTOF S and CHRISTIAN B. An ant colony optimization algorithm for continuous optimization: application to feed-forward neural network training[J]. Neural Computing and Applications, 2007, 16(3): 235–247 doi: 10.1007/s00521-007-0084-z

ROBERT C G, WANG Lingfeng, and MANSOOR A. Training neural networks using central force optimization and particle swarm optimization: Insights and comparisons[J]. Expert Systems with Applications, 2012, 39(1): 555–563 doi: 10.1016/j.eswa.2011.07.046

ZHANG Jingru, ZHANG Jun, LOCK T M, et al. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training[J]. Applied Mathematics and Computation, 2007, 185(2): 1026–1037 doi: 10.1016/j.amc.2006.07.025

CHEN Ke, ZHOU Fengyu, and LIU Aling. Chaotic dynamic weight particle swarm optimization for numerical function optimization[J]. Knowledge-Based Systems, 2018, 139: 23–40 doi: 10.1016/j.knosys.2017.10.011

LONG Wen, JIAO Jianjun, LIANG Ximing, et al. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization[J]. Engineering Applications of Artificial Intelligence, 2018, 68: 63–80 doi: 10.1016/j.engappai.2017.10.024

MURO C, ESCOBEDO R, SPECTOR L, et al. Wolf-pack hunting strategies emerge from simple rules in computational simulations[J]. Behavioral Processes, 2011, 88(3): 192–197 doi: 10.1016/j.beproc.2011.09.006

MIRJALILI S, MIRJALILI S M, and LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46–61 doi: 10.1016/j.advengsoft.2013.12.007

UDWADIA F E and GUTTALU R S. Chaotic dynamics of a piecewise cubic map[J]. Physical Review A, 1989, 40(7): 4032–4044 doi: 10.1103/PhysRevA.40.4032

龙文, 蔡绍洪, 焦建军, 等. 求解大规模优化问题的改进鲸鱼优化算法[J]. 系统工程理论与实践, 2017, 37(11): 2983–2994 doi: 10.12011/1000-6788(2017)11-2983-12

LONG Wen, CAI Shaohong, JIAO Jianjun, et al. Improved whale optimization algorithm for large scale optimization problems[J]. Systems Engineering-Theory &Practice, 2017, 37(11): 2983–2994 doi: 10.12011/1000-6788(2017)11-2983-12

AlI M H, MOHAMMED B A D A, ISMAIL A, et al. A new intrusion detection system based on fast learning network and particle swarm optimization[J]. IEEE Access, 2018, 6: 20255–20261 doi: 10.1109/ACCESS.2018.2820092

BLAKE C l and MERZ C J. UCI Repository of machine learning databases[OL]. http://archive.ics.uci.edu/ml/datasets.html, 1998.

施引文献

期刊类型引用(24)

1.	陈强，宫改花，张贾军. 基于超声波和北斗定位技术的作业范围自动化监测预警技术研究. 电子设计工程. 2025(03): 168-173 . 百度学术
2.	王勇，郑越峰，杨頔，周萌，王炳辉. 北斗卫星导航单点定位方法研究. 自动化仪表. 2025(01): 16-20 . 百度学术
3.	谢发荣，邓钰祺，胡健民，孙伟强，易堃. 基于CRPA技术的北斗/GPS对时系统误差校正. 电子设计工程. 2025(04): 146-150 . 百度学术
4.	王剑，王鹤，侯育红. 结合钟差解耦的GNSS精密单点定位. 地理空间信息. 2025(02): 15-19 . 百度学术
5.	章巍，储著宇，徐昊，金必都. 基于电子围栏与北斗定位算法的船舶偏航预警技术. 武汉理工大学学报(交通科学与工程版). 2025(01): 218-222 . 百度学术
6.	周勇祥，潘芳. 基于北斗卫星导航技术的隧道定位补盲系统建设研究. 科技资讯. 2025(02): 34-36 . 百度学术
7.	周志行，夏文龙，宋剑鹏，廖本钊，郭庆功. 北斗三号实时精密定位授时系统设计与实现. 信息技术与信息化. 2024(01): 184-187 . 百度学术
8.	薛卓，张存良，王亮，贾波. 基于北斗+5G技术的煤矿运输车辆定位控制. 自动化与仪表. 2024(04): 56-60 . 百度学术
9.	陈亮，展昕，赵胜，张志新. 非组合精密单点定位模型参数估计. 导航定位学报. 2024(01): 115-123 . 百度学术
10.	李伟，花洁. 基于GPS双定位的智慧接地线定位系统. 自动化技术与应用. 2024(06): 137-140+160 . 百度学术
11.	袁琨. 北斗卫星导航系统的精确定位方法分析. 集成电路应用. 2024(05): 322-323 . 百度学术
12.	蔡玉林，吴汤婷，范亚楠，全莹. 北斗GEO/IGSO/MEO卫星广播星历的轨道精度评估. 江西科学. 2024(05): 1027-1033 . 百度学术
13.	王博，武瑞宏，许双安，叶茂，邓川，张卫龙. 低成本亚米级PPP/INS组合导航定位系统研究. 铁道勘察. 2023(02): 8-13+43 . 百度学术
14.	柯腾伦，孙光辉，吴荣刚，丁凯生，陈睿容. 基于“当前”统计模型的卡尔曼滤波在北斗单向授时中的应用. 导航定位与授时. 2023(03): 39-48 . 百度学术
15.	矫殿成，何在民，马红皎，武建锋. 基于JFNG站的北斗PPP-B2b服务实时精密单点定位精度评估. 时间频率学报. 2023(02): 130-140 . 百度学术
16.	贾时蕾，王潜心. 基于两步Kalman滤波的NLoS误差抑制算法. 全球定位系统. 2023(05): 32-37 . 百度学术
17.	董静，宋洁文，王贝贝. 基于改进卡尔曼滤波的卫星导航定位精度优化. 北京测绘. 2023(09): 1291-1295 . 百度学术
18.	杨金明，马红皎. 基于“北斗”三号PPP-B2b的定位与时间传递. 电讯技术. 2023(12): 1951-1957 . 百度学术
19.	裴勇军，徐晓新，毛梅娟. 基于卡尔曼滤波算法的卫星导航高精度定位方法. 北京测绘. 2023(10): 1412-1417 . 百度学术
20.	尚琦. 基于授时服务与设备管理的电力北斗时频网研究. 长江信息通信. 2022(01): 110-112 . 百度学术
21.	倪志康，叶盛波，史城，潘俊，郑之杰，方广有. 一种深度学习辅助的探地雷达定位方法. 电子与信息学报. 2022(04): 1265-1273 . 本站查看
22.	刘旭. 手机PPP定位能力测试验证. 科技资讯. 2022(11): 7-9+116 . 百度学术
23.	李静，龙强，臧志斌，赵光，李朝阳，马胜. 北斗卫星导航系统在电力行业的应用研究. 电力信息与通信技术. 2022(10): 87-97 . 百度学术
24.	王在峰，张磊，尹彦坤，范志锋. 北斗系统在海洋工程中的应用探讨. 海洋信息技术与应用. 2022(03): 52-56 . 百度学术

其他类型引用(12)

资源附件(0)

访问统计

图(4) / 表(4)

计量

文章访问数: 1914
HTML全文浏览量: 774
PDF下载量: 102
被引次数: 36

1. 引言
2. 模型介绍
2.1 消电离层组合PPP模型
2.2 非组合PPP模型
2.3 参数估计
3. 静态PPP精密授时实验研究
3.1 数据采集与处理策略
3.2 静态PPP精密授时结果与分析
4. 动态PPP精密授时实验研究
4.1 数据采集与处理策略
4.2 动态PPP精密授时结果与分析
5. 结束语

1. 引言
2. 模型介绍
2.1 消电离层组合PPP模型
2.2 非组合PPP模型
2.3 参数估计
3. 静态PPP精密授时实验研究
3.1 数据采集与处理策略
3.2 静态PPP精密授时结果与分析
4. 动态PPP精密授时实验研究
4.1 数据采集与处理策略
4.2 动态PPP精密授时结果与分析
5. 结束语

参考文献(28)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

混沌灰狼优化算法训练多层感知器

doi: 10.11999/JEIT180519

作者简介:
晏福：男，1989年生，博士生，研究方向为智能优化算法、神经网络和数据挖掘

徐建中：男，1959年生，教授，博士生导师，研究方向为管理科学前沿研究

李奉书：男，1989年生，博士生，研究方向为管理科学前沿研究

通讯作者:
徐建中　xujianzhongxjz@163.com

计量

Training Multi-layer Perceptrons Using Chaos Grey Wolf Optimizer

1. 引言

2. 模型介绍

2.1 消电离层组合PPP模型

2.2 非组合PPP模型

2.3 参数估计

3. 静态PPP精密授时实验研究

3.1 数据采集与处理策略

3.2 静态PPP精密授时结果与分析

4. 动态PPP精密授时实验研究

4.1 数据采集与处理策略

4.2 动态PPP精密授时结果与分析

5. 结束语

期刊类型引用(24)

其他类型引用(12)

计量

目录

1. 引言

2. 模型介绍

2.1 消电离层组合PPP模型

2.2 非组合PPP模型

2.3 参数估计

3. 静态PPP精密授时实验研究

3.1 数据采集与处理策略

3.2 静态PPP精密授时结果与分析

4. 动态PPP精密授时实验研究

4.1 数据采集与处理策略

4.2 动态PPP精密授时结果与分析

5. 结束语

留言板

混沌灰狼优化算法训练多层感知器

doi: 10.11999/JEIT180519

作者简介: 晏福：男，1989年生，博士生，研究方向为智能优化算法、神经网络和数据挖掘 徐建中：男，1959年生，教授，博士生导师，研究方向为管理科学前沿研究 李奉书：男，1989年生，博士生，研究方向为管理科学前沿研究

通讯作者: 徐建中 xujianzhongxjz@163.com

计量

出版历程

Training Multi-layer Perceptrons Using Chaos Grey Wolf Optimizer

1. 引言

2. 模型介绍

2.1 消电离层组合PPP模型

2.2 非组合PPP模型

2.3 参数估计

3. 静态PPP精密授时实验研究

3.1 数据采集与处理策略

3.2 静态PPP精密授时结果与分析

4. 动态PPP精密授时实验研究

4.1 数据采集与处理策略

4.2 动态PPP精密授时结果与分析

5. 结束语

期刊类型引用(24)

其他类型引用(12)

计量

出版历程

目录

1. 引言

2. 模型介绍

2.1 消电离层组合PPP模型

2.2 非组合PPP模型

2.3 参数估计

3. 静态PPP精密授时实验研究

3.1 数据采集与处理策略

3.2 静态PPP精密授时结果与分析

4. 动态PPP精密授时实验研究

4.1 数据采集与处理策略

4.2 动态PPP精密授时结果与分析

5. 结束语

通讯作者:
徐建中　xujianzhongxjz@163.com