Area and Delay Optimization of Binary Decision Diagrams Mapped Circuit
-
摘要:
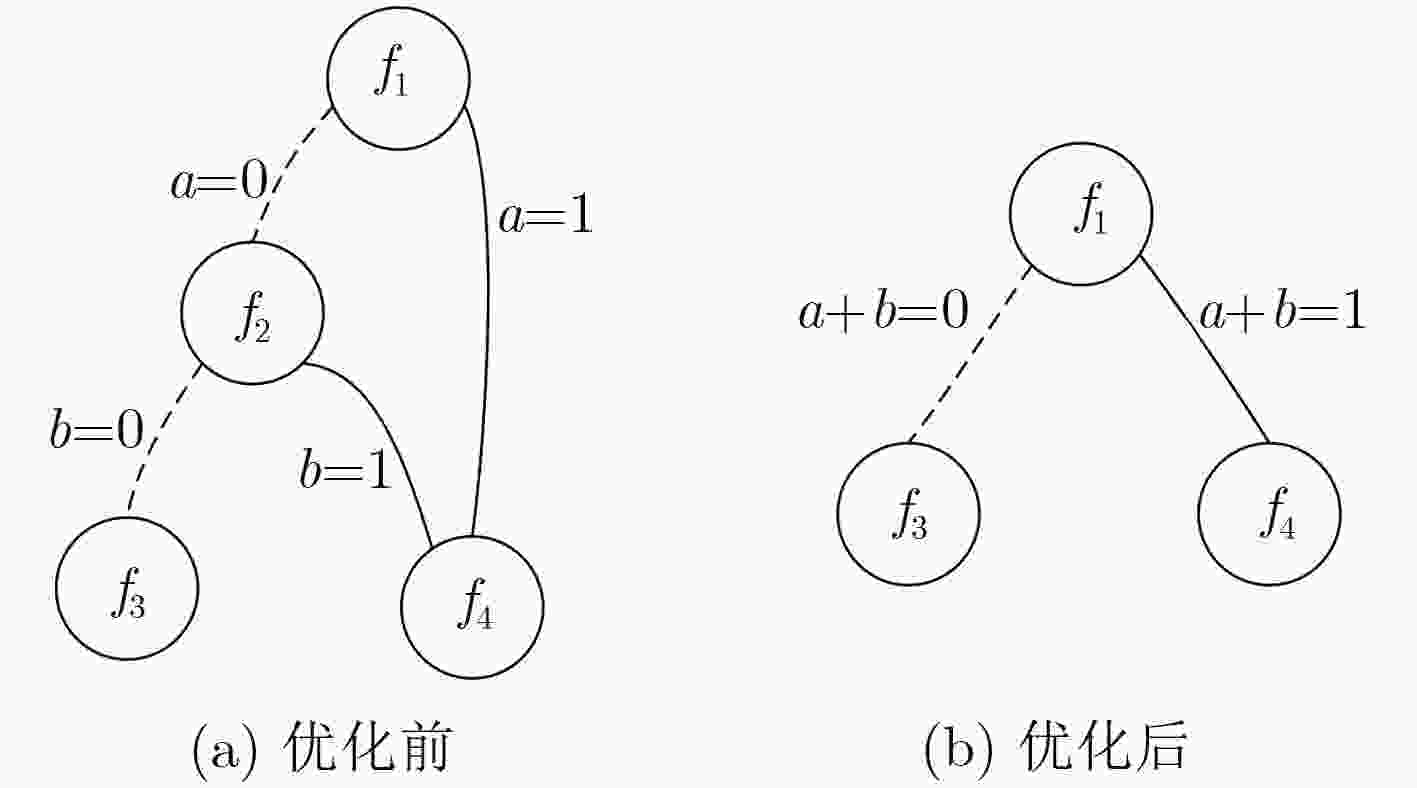
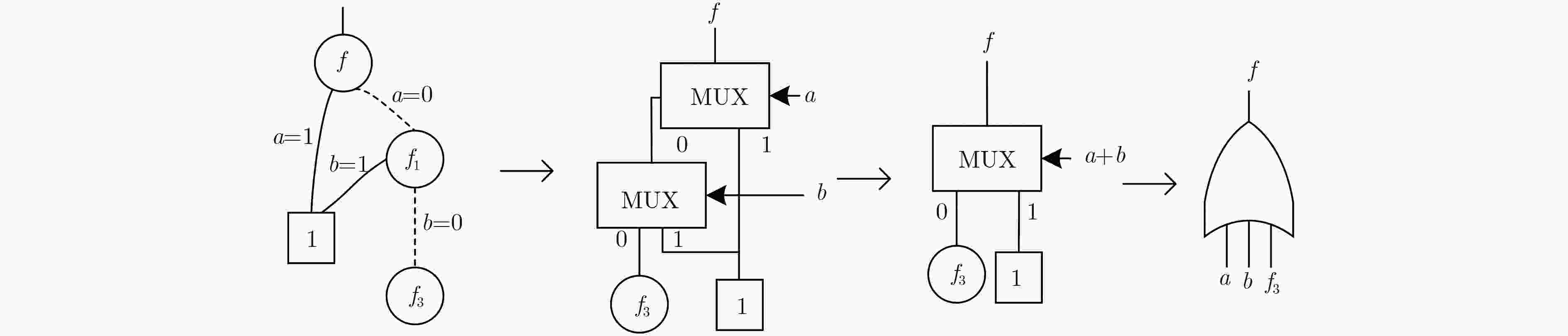
二叉决策图(BDD)是一种数据结构,广泛应用于数字电路的逻辑综合、测试和验证等领域。将BDD每个结点映射成2选1数据选择器(MUX)可得到BDD映射电路。该文提出一种BDD映射电路的面积和延时优化方法。首先把待优化电路转换成BDD形式,然后逐一搜索BDD中存在的菱形结构,进而通过路径优化实现结点的删减和控制变量的更改,并将所得结果BDD映射成MUX电路,最后用多个MCNC基准电路进行测试,将该文方法与经典综合工具BDS, SIS等方法相比较,BDD总结点数比BDS减少了55.8%,映射电路的面积和延时比SIS分别减小了39.3%和44.4%。
Abstract:Binary Decision Diagrams (BDD) is a data structure that can be used to describe a digital circuit. By replacing each node in a BDD with a 2-to-1 Multiplexer (MUX), a BDD can be mapped to a digital circuit. An area and delay optimization method on BDD mapped circuit is presented. A traditional Boolean circuit is converted into BDD form, and then diamond structure constructed by nodes is searched in the BDD, corresponding nodes are deleted and control signals of the modified nodes are updated by paths optimization, finally, the result BDD is mapped to a MUX circuit. The proposed method is test by a number of Microelectronics Center of North Carolina (MCNC) Benchmarks. Compared with the classical synthesis tools Sequential Interactive System (SIS) and BDD-based logic optimization System (BDS), the average number of nodes by the proposed methods is 55.8% less than that of BDS, and average circuit’s area and delay are reduced by 39.3% and 44.4% than that of the SIS, respectively.
-
Key words:
- Circuit optimization /
- Binary Decision Diagrams (BDD) /
- Multiplexer /
- Delay optimization
-
表 1 本文菱形结构BDD优化算法的伪代码
Begin algorithm Read_pla_benchmark_circuit(); Apply_CUDD_package(); //obtain circuit’s BDD Number_nodes(); //number nodes from 1 to num_of_BDD M=0; While (M<num_of_BDD) //handle all the non-terminals M=M+1; if(is_nodeM_diamond_structure()) //judge nodeM compute_mixed_paths(); reconstruct_BDD(); End if End while Output_logic_circuit(); Apply_area_model(); //calculate area and delay according to
modelApply_delay_model(); Output_results(); Free_memory_unit(); End algorithm 表 2 所提方法的结点优化情况
电路 输入/输出 原结点 BDS[12] DDBDD[14] 本文方法 结点 时间(s) 结点 时间(s) 结点 时间(s) rate1(%) rate2(%) rd84 8/4 42 73 0.02 84 0.20 19 0.03 73.97 77.38 cordic 23/2 42 49 0.01 66 0.18 39 0.10 20.41 40.91 b12 15/9 55 51 0.01 70 0.18 51 0.01 0 27.14 misex2 25/18 80 71 0.01 93 0.21 78 0.02 –9.86 16.13 duke2 22/29 336 485 0.23 612 1.77 330 0.32 31.96 46.08 in4 32/20 350 371 0.53 412 1.43 346 0.36 6.74 16.02 alu4 14/8 566 1004 0.58 1244 4.78 544 0.78 45.82 56.27 pdc 16/40 602 619 0.49 1042 22.40 572 0.93 7.59 45.11 table5 17/15 667 2276 1.95 2567 17.34 663 0.59 70.87 74.17 table3 14/14 751 2326 1.27 2246 21.24 744 0.75 68.01 66.87 mainpla 27/54 1766 4671 6.70 5347 38.24 1748 4.78 62.58 67.31 b4 33/23 188 — — 435 1.54 180 1.43 — 58.62 cps 24/108 971 — — 1415 16.42 958 1.65 — 32.30 平均 34.37 48.02 表 3 所提方法的面积(a.u.)和延时(a.u.)优化情况
电路 输入/输出 SIS[17] BBDD[7] CGMP[18] 本文方法 ratea/rated(%) 面积 延时 面积 延时 面积 延时 面积 延时 SIS BBDD CGMP cordic 23/2 194 11 225 14 164 16 162 16 16.5/–45.5 28.0/–14.3 1.2/0 9sym 9/1 528 14 90 7 176 7 125 7 76.3/50.0 –38.9/0 29.0/0 rd84 8/4 402 14 190 7 215 6 166 6 58.7/57.1 12.6/14.3 22.8/0 t2 16/13 645 17 890 13 620 10 483 12 25.1/29.4 45.7/7.7 22.1/–20.0 duke2 22/29 1598 20 4410 17 1836 16 1438 15 10.0/25.0 67.4/11.8 21.7/6.3 alu4 14/8 1614 13 3000 13 2986 8 2532 8 –56.9/38.5 15.6/38.5 15.2/0 misex3 14/14 3668 21 4480 12 2530 8 2030 6 44.7/71.4 54.7/50.0 19.8/25.0 bc0 26/11 4025 24 6250 20 2640 16 2191 15 45.6/37.2 64.9/25.0 17.0/6.3 e64 65/64 4235 16 640 64 1453 12 639 7 84.9/56.3 0.2/89.1 56.0/41.7 table5 17/15 5069 24 4660 15 3024 14 2863 11 43.5/54.2 38.6/26.7 5.3/21.4 table3 14/14 5230 23 4365 12 3876 8 3473 8 33.6/65.2 20.4/33.3 10.4/0 cps 24/108 5525 20 — — 5013 17 3990 14 27.8/30.0 — 20.4/17.6 平均 34.2/39.1 28.1/25.6 20.1/8.2 -
DAS A, DEBNATH A, and PRADHAN S. Area, power and temperature optimization during binary decision diagram based circuit synthesis[C]. Devices for Integrated Circuit, Kalyani, India, 2017: 778–782. 符强, 汪鹏君, 王铭波, 等. 求解FPRM电路极性优化问题的改进多目标粒子群算法[J]. 计算机辅助设计与图形学学报, 2018, 30(3): 540–548. doi: 10.3724/SP.J.1089.2018.16297FU Qiang, WANG Pengjun, WANG Mingbo, et al. An improved multi-objective particle swarm optimization algorithm for polarity optimization of FPRM circuits[J]. Journal of Computer-Aided Design &Computer Graphics, 2018, 30(3): 540–548. doi: 10.3724/SP.J.1089.2018.16297 符强, 汪鹏君, 童楠, 等. 基于MODPSO算法的FPRM电路多约束极性优化方法[J]. 电子与信息学报, 2017, 39(3): 717–723. doi: 10.11999/JEIT160458FU Qiang, WANG Pengjun, TONG Nan, et al. Multi-constrained polarity optimization of large-scale FPRM circuits based on multi-objective discrete particle swarm optimization[J]. Journal of Electronics &Information Technology, 2017, 39(3): 717–723. doi: 10.11999/JEIT160458 YU Cunxi, CIESIELSKI M, and MISHCHENKO A. Fast algebraic rewriting based on and-inverter graphs[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, 37(9): 1907–1911. doi: 10.1109/TCAD.2017.2772854 NOUREDDINE M and ZARAKET F. Model checking software with first order logic specifications using AIG solvers[J]. IEEE Transactions on Software Engineering, 2016, 42(8): 741–763. doi: 10.1109/TSE.2016.2520468 CHUN Chechung, YUNG Chichen, CHUN Yaowang, et al. Majority logic circuits optimisation by node merging[C]. Design Automation Conference, Chiba, Japan, 2017: 714–719. AMARU L. New Data Structures and Algorithms for Logic Synthesis and Verification[M]. Switzerland: Springer International Publishing, 2017: 17–19. FRIED D, TABAJARA L M, and VARDI M Y. BDD-Based boolean functional synthesis[C]. International Conference on Computer Aided Verification, Toronto, Canada, 2016: 402–421. MESKI A, PENZEK W, SZRETER M, et al. BDD-versus SAT-based bounded model checking for the existential fragment of linear temporal logic with knowledge: Algorithms and their performance[J]. Autonomous Agents and Multi-Agent Systems, 2014, 28(4): 558–604. doi: 10.1007/s10458-013-9232-2 KERTTU M, LINDGREN P, DRECHSLER R, et al. Low power optimization yechnique for BDD mapped finite state machines[C]. International Workshop on Logic & Synthesis, San Diego, USA, 2007: 143–148. SHIRINZADEH S, SOEKEN M, and DRECHSLER R. Multi-objective BDD optimization with evolutionary algorithms[C]. Conference on Genetic & Evolutionary Computation, Madrid, Spain, 2015: 751–758. YANG Congguang and CIESIELSKI M. BDS: A BDD-based logic optimization system[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2002, 21(7): 866–876. doi: 10.1109/TCAD.2002.1013899 KUBICA M and KANIA D. SMTBDD: New form of BDD for logic synthesis[J]. International Journal of Electronics and Telecommunications, 2016, 62(1): 33–41. doi: 10.1515/eletel-2016-0004 CHENG Lei, CHEN Deming, and WONG M. Martin DDBDD: Delay-Driven BDD synthesis for FPGAs[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2008, 27(7): 1203–1213. doi: 10.1109/TCAD.2008.923088 SOMENZI F. CUDD: CU Decision Diagram package release 3.0.0[OL]. http://vlsi.colorado.edu/~fabio/CUDD, 2017. BRACE K S, RUDELL R L, and BRYANT R E. Efficient implementation of a BDD package[C]. IEEE Design Automation Conference, Orlando, USA, 1991, 40–45. SENTOVICH E M, SINGH K J, LAVAGNO L, et al. SIS: A system for sequential circuit synthesis[OL]. https://embedded.eecs.berkeley.edu/pubs/downloads/sis/index.htm, 2017. 岑旭梦, 王伦耀, 夏银水. 基于逻辑复合门映射的电路面积优化[J]. 宁波大学学报, 2016, 29(4): 38–43.CEN Xumeng, WANG Lunyao, and XIA Yinshui. Area optimization based on the complex logic gates mapping[J]. Journal of Ningbo University (NSEE) , 2016, 29(4): 38–43. -





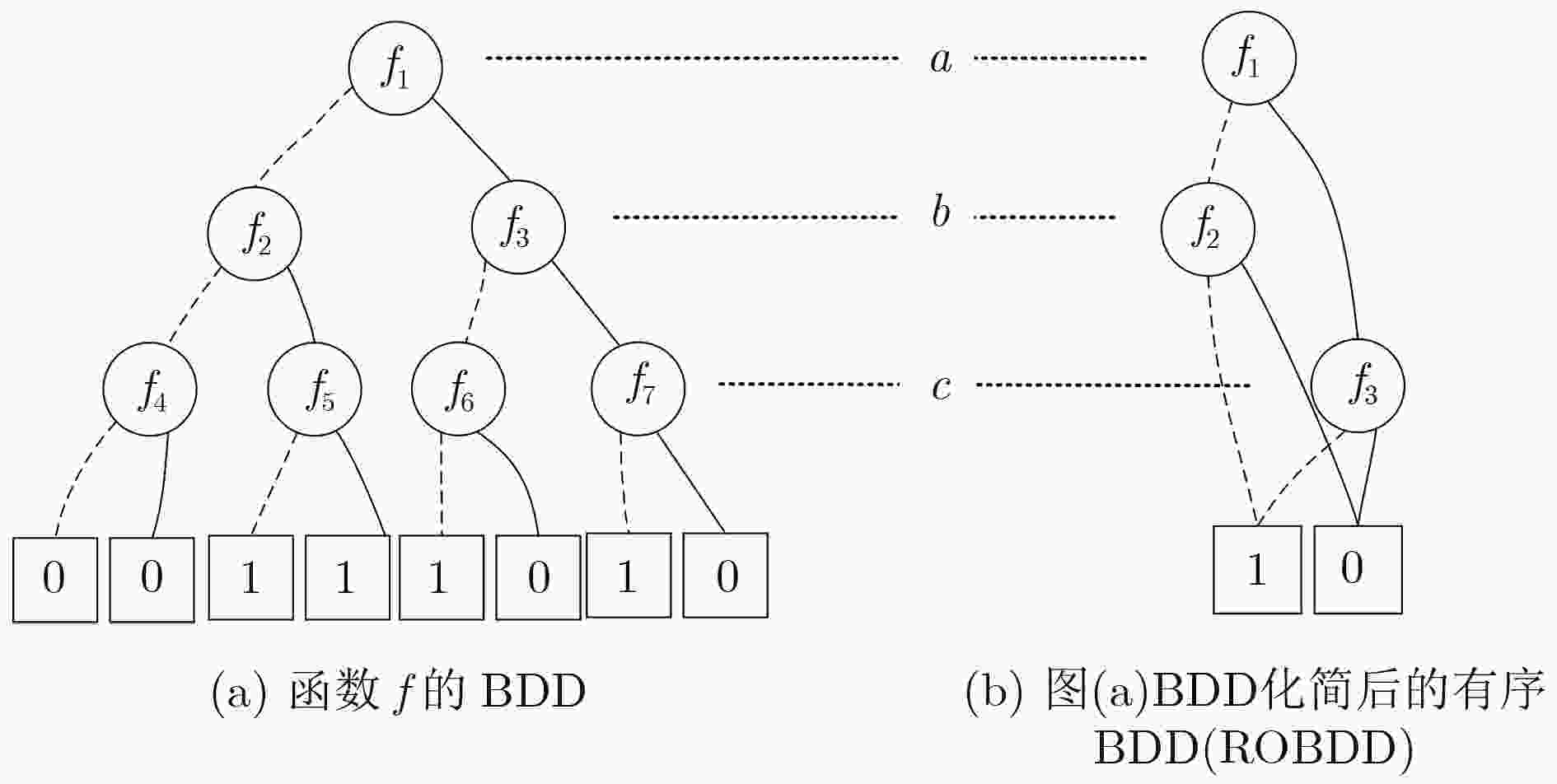
 下载:
下载:
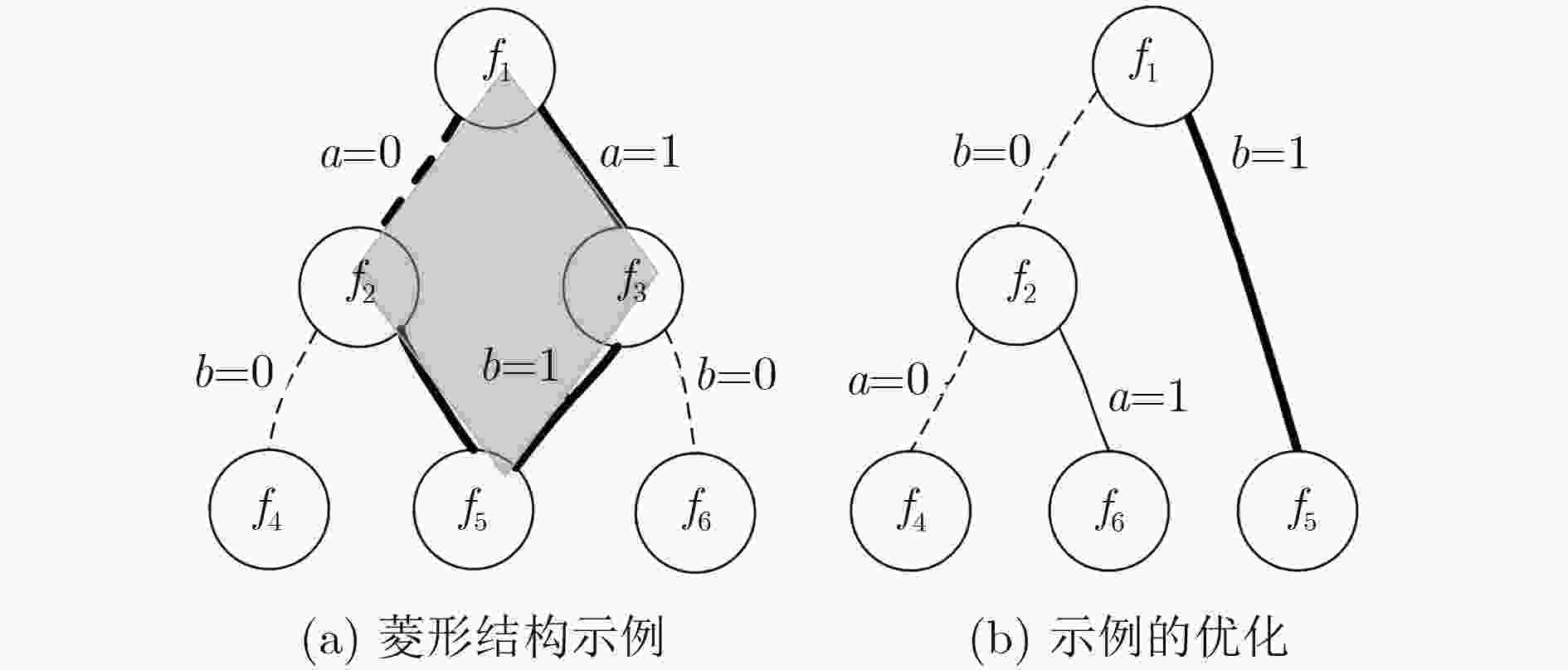
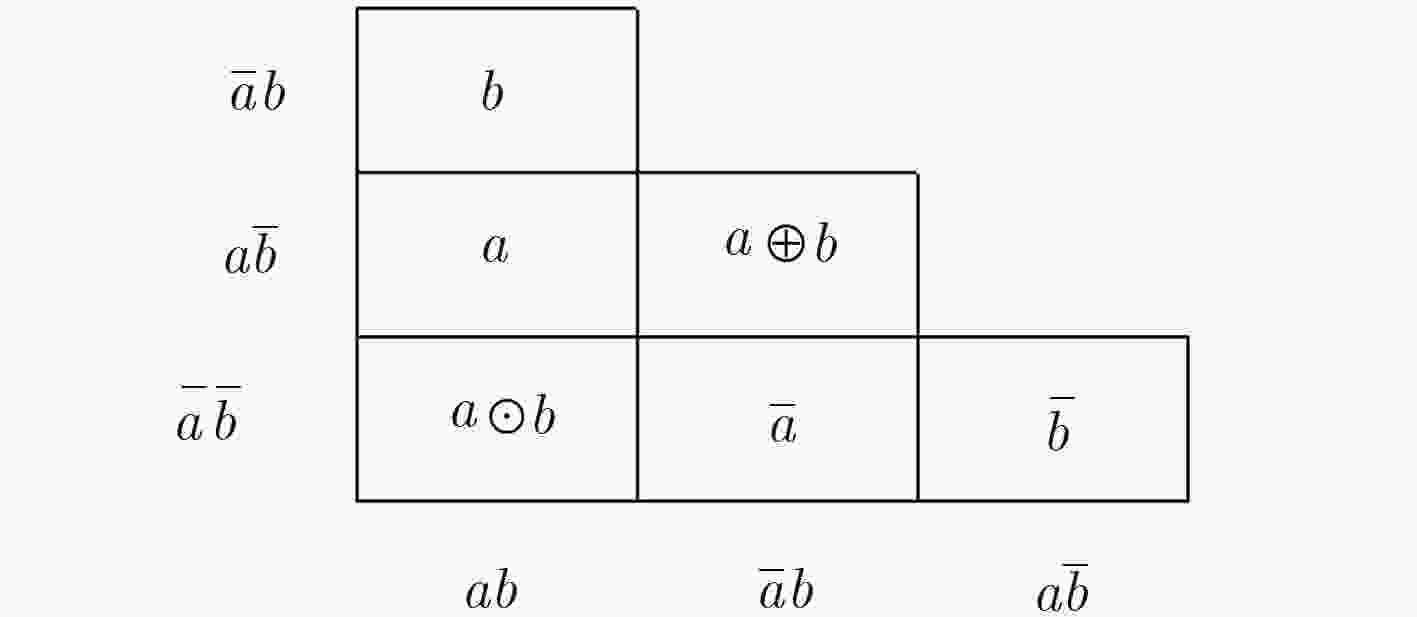
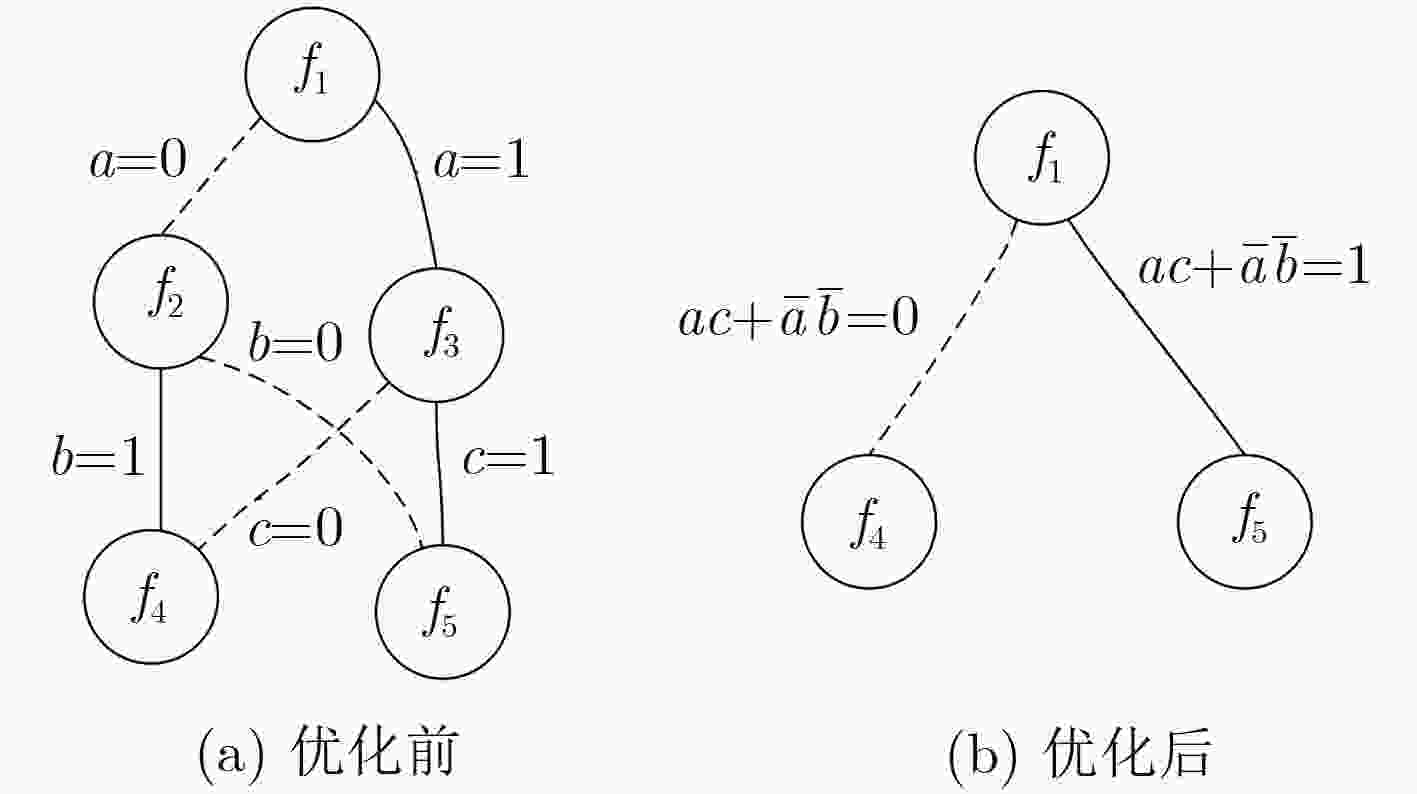


 下载:
下载:
