Frequency Sorting Algorithm Based on Dynamic Ring Oscillator Physical Unclonable Function Statistical Model
-
摘要:
针对现有环形振荡器物理不可克隆函数(ROPUF)设计存在的可靠性和唯一性不高,导致在应用时安全性较差的问题,该文提出面向ROPUF的统计模型,定量分析了可靠性和唯一性的影响因素,发现增大延迟差能够提高可靠性,减小环形振荡器(RO)单元间的工艺差异可以提高唯一性。根据该模型结论,设计了基于mesh拓扑结构的动态RO单元,结合RO阵列频率分布特性,设计了一种新的频率排序算法,以增大延迟差和减小RO单元的工艺差异,从而提高ROPUF的可靠性和唯一性。结果表明,与其他改进设计的ROPUF相比,所提设计的可靠性和唯一性具有显著优势,可达到99.642%和49.1%,且受温度变化的影响最小。安全性分析证明,该文的设计具有很强的抗建模攻击能力。
Abstract:The existing Ring Oscillator (RO) Physical Unclonable Function (ROPUF) design has low reliability and uniqueness, resulting in poor application security. A statistical model for ROPUF is proposed, the factors of reliability and uniqueness are quantitatively analyzed, it is found that the larger delay difference can improve the reliability, and the lower process difference between RO units can improve the uniqueness. According to the conclusion of the model, a dynamic RO unit is designed based on the mesh topological structure. In combination with the frequency distribution characteristics of the RO array, a new frequency sorting algorithm is designed to increase the delay difference and reduce the process variation of the RO unit, thereby improving the reliability and uniqueness of ROPUF. The results show that compared with other improved ROPUF designs, the reliability and uniqueness of the proposed design has significant advantages, which can reach 99.642% and 49.1%, and temperature changes affect minimally them. It is verified by security analysis that the proposed design has strong anti-modeling attack capabilities.
-
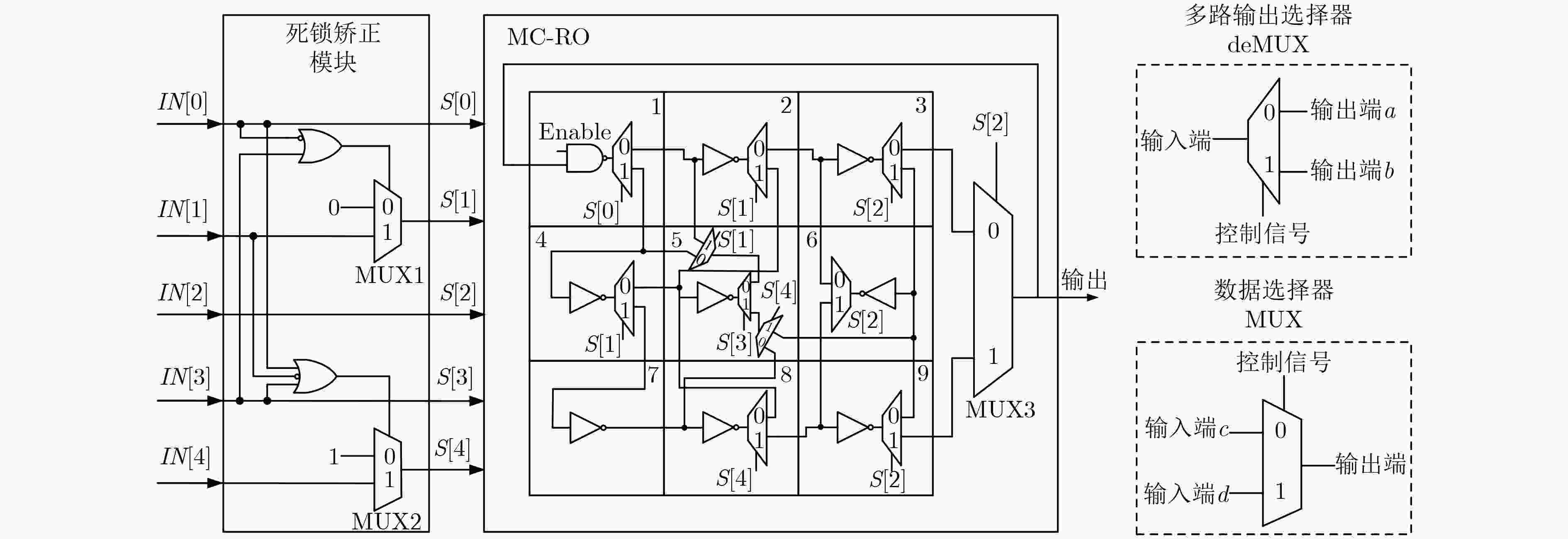
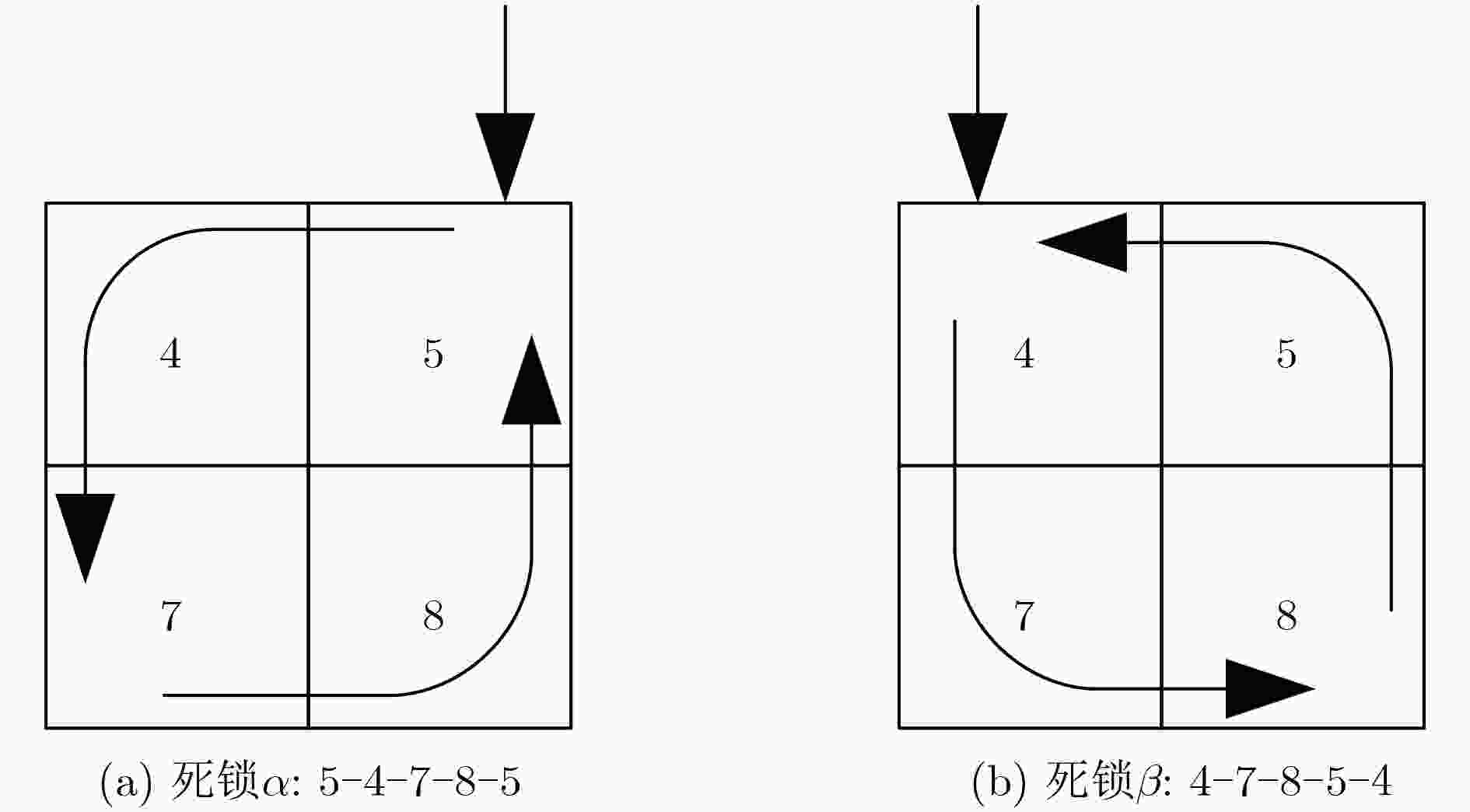
表 1 死锁矫正方案
S[0] S[3] S[1] 是否存在死锁(是/否) 矫正方案 S[4] S[1] 0 0 1 是 1 – 0 1 0/1 否 0/1 – 1 0 – 是 – 0 1 1 – 否 – 0/1 表 2 频率比较结果的概率分布
RO级数 3 5 7 9 概率 3 0/1 1 1 1 ${\rho _{\rm{A}}}$ 5 0 0/1 1 1 ${\rho _{\rm{B}}}$ 7 0 0 0/1 1 ${\rho _{\rm{C}}}$ 9 0 0 0 0/1 ${\rho _{\rm{D}}}$ 概率 ${\rho _{\rm{A}}}$ ${\rho _{\rm{B}}}$ ${\rho _{\rm{C}}}$ ${\rho _{\rm{D}}}$ 100% 表 3 频率排序算法伪代码
算法 1 频率排序算法(FSA) (1) for C determining CLB-X do (2) $F = \{ f(x,1),f(x,2), ·\!·\!· ,f(x,N)\} $; (3) for i=1 to N do (4) ${Z_i} = {\rm COUNTER}(f(x,i))$; (5) end for (6) $\bar Z = {{\left( {{Z_1} + {Z_2} + ·\!·\!· + {Z_N}} \right)} / N}$; (7) for i=1 to N do (8) ${d_i} = \left| {{Z_i} - \bar Z} \right|$; (9) end for (10) if (x>y) then (11) gt(x, y)=1 (12) else (13) gt(x, y)=0 (14) end if (15) for k=1 to N–1 do (16) for j=1 to k do (17) S1=0 (18) ${L_k} = {S_j} + gt\left( {{d_{k + 1}},{d_j}} \right)$; (19) end for (20) end for (21) $R = {\rm Gray}\left( {{L_1}} \right){\rm{|}}|{\rm Gray}\left( {{L_2}} \right){\rm{|}}| ·\!·\!· |{\rm{|}}{\rm Gray}\left( {{L_{N - 1}}} \right)$; (22) end for (23) return (R) 表 4 性能指标分析对比
表 5 RO单元资源利用效率对比
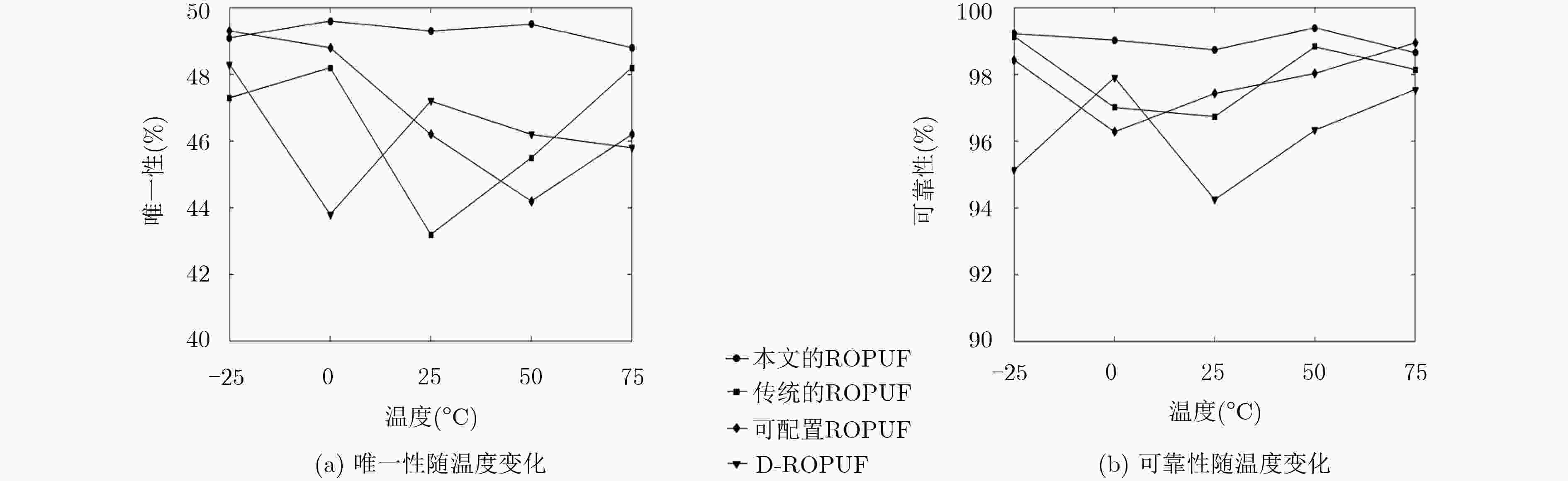
指标 传统的ROPUF 可配置ROPUF D-ROPUF 本文的ROPUF CLB数量 2 1 1 2 Slice数量 5 3 4 4 LUT数量 6 6 8 15 RO单元可产生频率数 1 8 4 18 抗建模攻击能力 传统的ROPUF<D-ROPUF<可配置ROPUF<本文的ROPUF 表 6 破解不同规格PUF所需攻击次数的比较
t N Q 2 8 1.04×1011 18 8 1.35×1075 36 8 2.47×10176 18 16 1.99×10258 36 16 3.85×10502 -
GASSEND B, CLARKE D, DEVADAS S, et al. Silicon physical random functions[C]. ACM Conference on Computer and Communications Security, Washington, USA, 2002: 148–160. XU Xiaolin, BURLESON W, and HOLCOMB D E. Using statistical models to improve the reliability of delay-based PUFs[C]. 2016 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Pittsburgh, USA, 2016: 547–552. STANCIU A, MOLDOVEANU F D, and CIRSTEA M. A novel PUF-based encryption protocol for embedded System on Chip[C]. International Conference on Development and Application Systems, Suceava, Romania, 2016: 158–165. MAITI A and SCHAUMONT P. Improved ring oscillator PUF: An FPGA-friendly secure primitive[J]. Journal of Cryptology, 2004, 24(2): 375–397. doi: 10.1007/s00145-010-9088-4 AMSAAD F, CHOUDHURY M, CHAUDHURI C R, et al. An innovative delay based algorithm to boost PUF security against machine learning attacks[C]. Industrial Electronics, Technology & Automation, Bridgeport City, USA, 2017: 1–6. MAES R, HERREWEGE A V, and VERBAUWHEDE I. PUFKY: A fully functional PUF-based cryptographic key generator[C]. International Conference on Cryptographic Hardware and Embedded Systems, Leuven, Belgium, 2012: 302–319. LIU Weiqiang, YU Yifei, WANG Chenghua, et al. RO PUF design in FPGAs with new comparison strategies[C]. IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 2015: 77–80. KODYTEK F, LORENCZ R, BUCEK J, et al. Temperature dependence of ROPUF on FPGA[C]. Digital System Design, Limassol, Cyprus, 2016: 698–702. CHANG Hongliang and SACHIN S. Statistical timing analysis considering spatial correlation in a pert-like traversal[C]. International Conference on Computer Aided Design, San Jose, USA, 2003: 621–625. HADDAD P, FISCHER V, BERNARD F, et al. A physical approach for stochastic modeling of TERO-based TRNG[C]. International Conference on Cryptographic Hardware and Embedded Systems, Saint-Malo, France, 2015: 357–372. HERDER C, YU M D, KOUSHANFAR F, et al. Physical unclonable functions and applications: A tutorial[J]. Proceedings of the IEEE, 2014, 102(8): 1126–1141. doi: 10.1109/JPROC.2014.2320516 KODYTEK F, LORENCZ R, and BUCEK J. Improved ring oscillator PUF on FPGA and its properties[J]. Microprocessors & Microsystems, 2016, 47(1): 55–63. doi: 10.1016/j.micpro.2016.02.005 RAHMAN M T, FORTE D, RAHMAN F, et al. A pair selection algorithm for robust RO-PUF against environmental variations and aging[C]. IEEE International Conference on Computer Design, New York, USA, 2015: 415–418. RUHRMAIR U, SOLTER J, SEHNKE F, et al. PUF modeling attacks on simulated and silicon data[J]. IEEE Transactions on Information Forensics & Security, 2013, 8(11): 1876–1891. doi: 10.1109/TIFS.2013.2279798 项群良, 张培勇, 欧阳冬生, 等. 多频率段物理不可克隆函数[J]. 电子与信息学报, 2012, 34(8): 2007–2012. doi: 10.3724/SP.J.1146.2011.01249XIANG Qunliang, ZHANG Peiyong, OUYANG Dongsheng, et al. An introduction to multi-frequency segment physical unclonable function[J]. Journal of Electronics &Information Technology, 2012, 34(8): 2007–2012. doi: 10.3724/SP.J.1146.2011.01249 -





 下载:
下载:


 下载:
下载:
