混响室条件下线缆共模干扰临界辐射干扰场强测试研究

胡德洲; 魏光辉; 潘晓东; 卢新福

doi:10.11999/JEIT180328

混响室条件下线缆共模干扰临界辐射干扰场强测试研究

doi: 10.11999/JEIT180328

陆军工程大学电磁环境效应国家级重点实验室石家庄 050003

基金项目: 国家自然科学基金(61372040)

详细信息

作者简介:
胡德洲：男，1990年生，博士生，研究方向为电磁环境效应试验评估技术

魏光辉：男，1964年生，教授，博士生导师，研究方向为电磁兼容与防护技术

潘晓东：男，1980年生，讲师，博士，研究方向为电磁兼容与防护技术

卢新福：男，1988年生，博士，研究方向为电磁环境效应试验评估技术

通讯作者:
胡德洲　hdz199075@sina.cn

中图分类号: TN06
计量
- 文章访问数: 1867
- HTML全文浏览量: 744
- PDF下载量: 53
- 被引次数: 0
出版历程
- 收稿日期: 2018-04-11
- 修回日期: 2018-12-13
- 网络出版日期: 2018-12-20
- 刊出日期: 2019-04-01

Investigation on the Radiated Interference E-field Threshold Testing for Common-mode Interference of Transmission Lines in Reverberation Chambers

National Key Laboratory on Electromagnetic Environment Effects, Army Engineering University, Shijiazhuang 050003, China

Funds: The National Natural Science Foundation of China (61372040)

摘要

摘要:
为在混响室中线缆共模干扰时的设备(EUT)进行临界辐射干扰场强测试，并确保与开阔场中测试结果一致，该文推导了线缆上共模电流满足的方程，将共模电流分解为相应的特征电流，计算了终端负载任意时线缆最大方向性系数的变化范围。以单导体传输线和同轴线为EUT，分别在混响室和开阔场中测试线缆的临界干扰场强，对计算结果进行了验证。结果表明：最大方向性系数的计算结果可以保证两种不同场地中测试结果的一致性，双线的共模干扰以及同轴线均可以等效为单线，且线缆弯曲对测试结果基本没有影响。
- 混响室 /
- 临界干扰场强 /
- 线缆 /
- 方向性系数
Abstract:
To test the radiated interference E-field threshold of Equipment Under Test (EUT) with common-mode interference of transmission lines in reverberation chambers and unify the test results with the open areas, the range of the maximum directivity of the lines with random loads is calculated by the derivation of the equation of the common-mode currents and decomposition of the currents into the corresponding characteristic ones. The calculated results are validated with the experiments performed in a reverberation chamber and an open area, respectively, with a single conductor line and a coaxial cable as the EUT. The theoretical and experimental results show that the test results in the two different areas can be unified with the calculated results. The common mode interference of two conductor lines and coaxial cables can be equivalent to single conductor lines and the bend of the lines almost has no influence on the test results.
- Reverberation chamber /
- Radiated interference E-field threshold /
- Transmission line /
- Directivity

HTML全文

图 1 共模干扰特征电流

下载: 全尺寸图片幻灯片

图 2 特征电流辐射场

下载: 全尺寸图片幻灯片

图 3 双导体传输线共模干扰时D_max的范围

下载: 全尺寸图片幻灯片

图 4 单线D_max的范围

下载: 全尺寸图片幻灯片

图 5 P与W_s关系示意图

下载: 全尺寸图片幻灯片

图 6 混响室与开阔场临界场强比较

下载: 全尺寸图片幻灯片

图 7 直线和弯线接收功率平均值比较

下载: 全尺寸图片幻灯片

图 8 混响室与开阔场临界场强比较(同轴线)

下载: 全尺寸图片幻灯片

表 1 混响室中参数计算结果(单线)

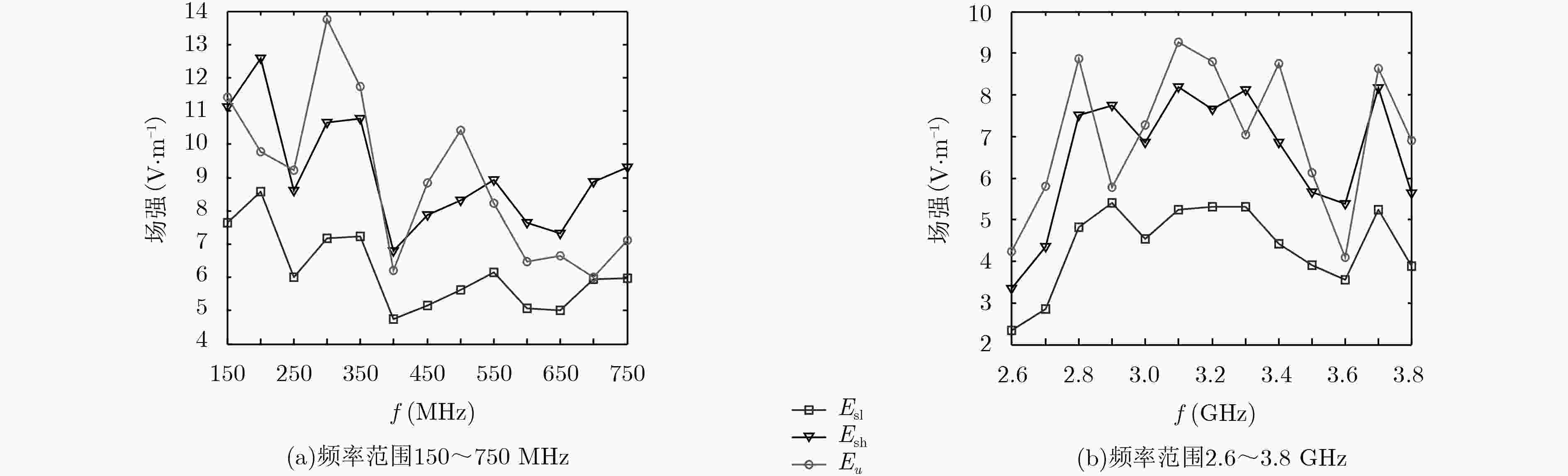
f (GHz)	D_{max, h}	D_{max, l}	$\sigma $ (V·m^–1)	W_s (dBm)	E_sh (V·m^–1)	E_sl (V·m^–1)
0.15	2.72	1.28	5.73	17.76	9.86	8.95
0.20	2.86	1.33	6.60	20.60	11.32	10.55
0.25	3.36	1.64	5.01	15.06	10.01	8.71
0.30	4.06	1.85	6.59	15.54	11.78	9.85
0.35	4.18	1.89	4.38	14.67	9.79	7.61
0.40	4.68	2.29	4.68	10.38	6.68	5.25
0.45	5.30	2.28	5.40	10.77	7.99	6.63
0.50	5.34	2.43	5.89	9.70	9.02	7.65
0.55	5.86	2.77	6.76	12.15	10.36	8.77
0.60	6.43	2.82	5.84	11.31	8.30	7.09
0.65	6.38	3.01	5.76	9.78	7.51	6.04
0.70	6.94	3.11	7.13	10.73	8.17	6.30
0.75	7.48	3.06	7.41	11.83	8.35	6.56
2.60	16.49	8.16	9.46	–10.7	3.44	2.75
2.70	17.38	7.44	5.42	–6.56	4.73	3.99
2.80	18.09	7.38	9.30	–3.16	7.53	6.08
2.90	17.75	8.63	10.34	–2.20	7.38	5.71
3.00	18.56	8.16	8.91	–5.72	7.04	5.84
3.10	19.40	8.01	10.53	–4.96	8.83	7.32
3.20	18.97	9.16	10.55	–5.08	7.60	6.02
3.30	19.79	8.50	10.76	–9.74	7.71	5.94
3.40	20.70	8.60	9.15	–9.05	7.26	6.07
3.50	20.12	9.57	7.98	–12.65	6.23	5.08
3.60	20.87	9.10	7.38	–10.99	4.97	3.81
3.70	21.89	9.03	11.16	–1.89	7.95	6.41
3.80	21.34	10.12	8.15	–6.18	6.35	5.32

下载: 导出CSV

表 2 混响室中参数计算结果(同轴线)

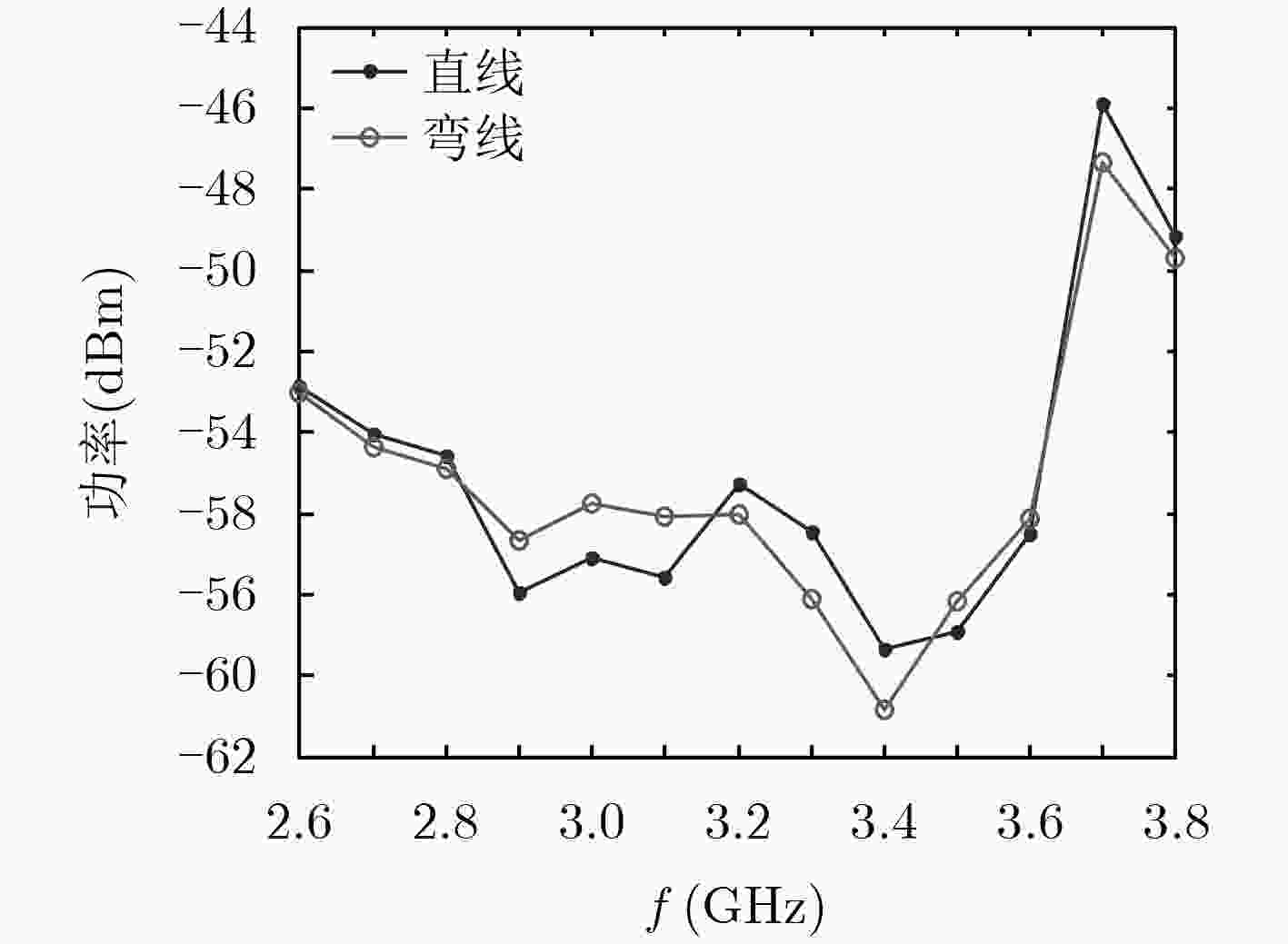
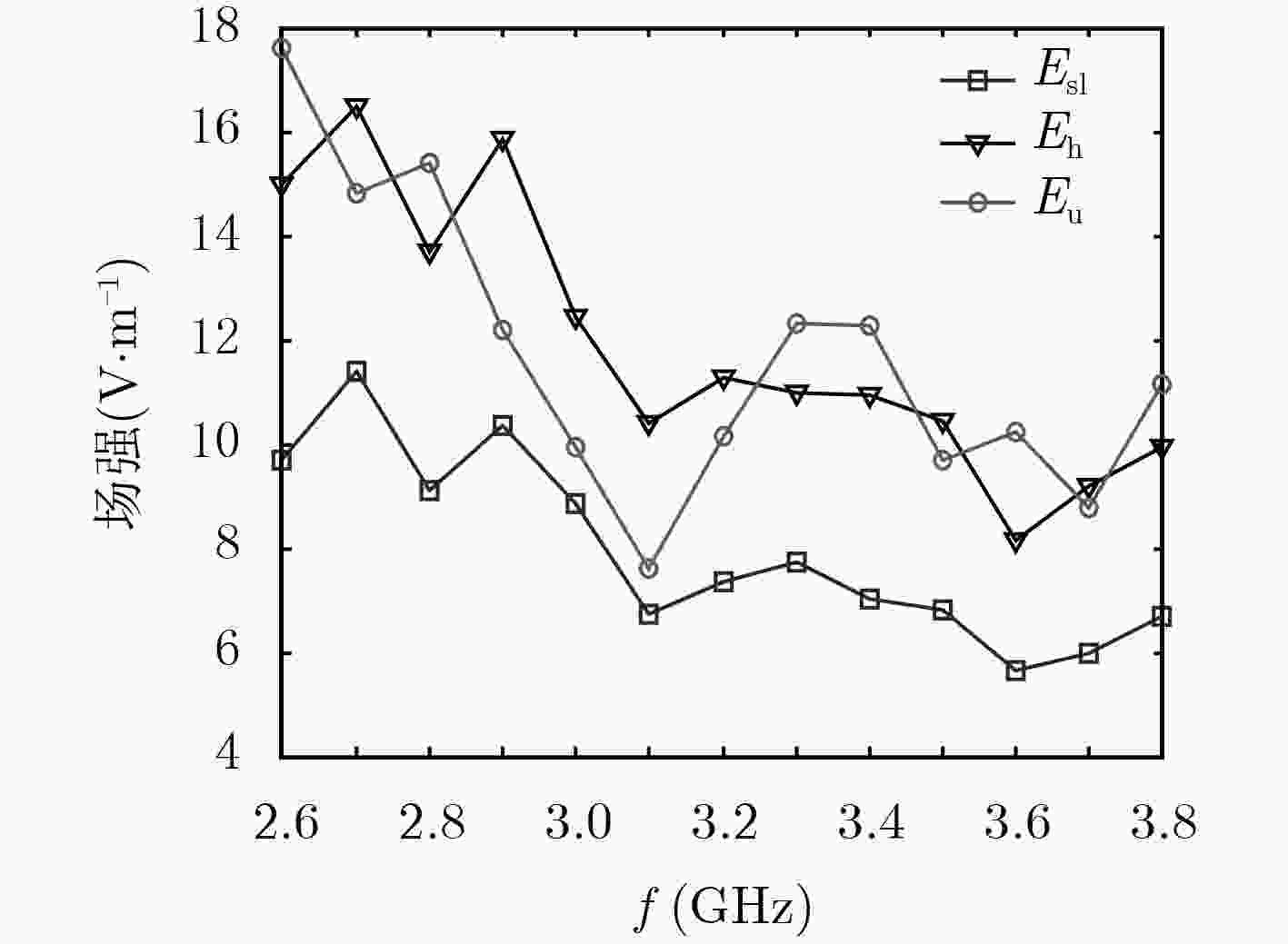
f (GHz)	D_{max, h}	D_{max, l}	$\sigma $ (V·m^–1)	W_s (dBm)	E_sh (V·m^–1)	E_sl (V·m^–1)
2.6	16.85	7.01	18.07	–50.82	15.00	9.67
2.7	16.49	7.89	21.06	–52.00	16.48	11.40
2.8	17.26	7.59	17.18	–52.50	13.70	9.09
2.9	17.98	7.67	19.97	–55.88	15.84	10.35
3.0	17.64	8.95	16.93	–55.01	12.43	8.85
3.1	18.54	7.78	13.18	–55.50	10.38	6.72
3.2	19.08	8.09	14.60	–53.20	11.28	7.34
3.3	18.75	9.25	15.23	–54.40	11.00	7.73
3.4	20.01	8.26	14.32	–57.29	10.95	7.03
3.5	20.14	8.61	13.95	–56.83	10.45	6.83
3.6	19.86	9.46	11.41	–54.43	8.15	5.63
3.7	21.16	9.03	12.54	–43.85	9.17	5.99
3.8	21.04	9.52	13.97	–47.08	9.95	6.69

下载: 导出CSV

参考文献(27)

AMADOR E, KRAUTHAUSER H G, and BESNIER P. A binomial model for radiated immunity measurements[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(4): 683–691 doi: 10.1109/TEMC.2012.2231942

SELEMANI K, RICHALOT E, LEGRAND O, et al. Energy localization effects within a reverberation chamber and their reduction in chaotic geometries[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(2): 325–333 doi: 10.1109/TEMC.2016.2617322

ARNAUT L R, MOGLIE F, BASTIANELLI L, et al. Helical stirring for enhanced low-frequency performance of reverberation chambers[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(4): 1016–1026 doi: 10.1109/TEMC.2016.2641386

MIGLIACCIO M, GIL J J, SORRENTINO A, et al. The polarization purity of the electromagnetic field in a reverberating chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(3): 694–700 doi: 10.1109/TEMC.2016.2528503

MONSEF f, SERRA R, and COAAZ A. Goodness-of-fit tests in reverberation chambers: Is sample independence necessary?[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(6): 1748–1751 doi: 10.1109/TEMC.2015.2451211

GJB151B-2013: 军用设备和分系统电磁发射和敏感度要求与测量[S]. 国军标2013.

GJB151B-2013: Electromagnetic emission and susceptibility requirements and measurements[S]. China Military Standard 2013.

IEC 61000-4-21: ElectroMagnetic Compatibility (EMC)-Part4-21: Testing and measurement techniques-reverberation chamber test methods[S]. IEC Standard 2008.

贾锐, 王庆国, 王树峤, 等. 混响室条件下辐射敏感度表征方法研究[J]. 北京理工大学学报, 2016, 36(1): 100–104

JIA Rui, WANG Qingguo, WANG Shuqiao, et al. Research on the characterization of susceptibility threshold in reverberation chamber[J]. Transactions of Beijing Institute of Technology, 2016, 36(1): 100–104

熊久良, 刘心愿. 基于位置替代法的无线电引信混响室敏感度测试方法[J]. 高电压技术, 2015, 41(1): 320–326 doi: 10.13336/j.1003-6520.hve.2015.01.045

XIONG Jiuliang and LIU Xinyuan. Susceptibility test method of radio fuze in reverberation chamber based on position substitution method[J]. High Voltage Engineering, 2015, 41(1): 320–326 doi: 10.13336/j.1003-6520.hve.2015.01.045

AMADOR E, MIRY C, and BOUYGE N. Compatible susceptibility measurements in fully anechoic room and reverberation chamber[C]. Proceeding of the 2014 International Symposium on Electromagnetic Compatibility (EMC Europe 2014). Gothenburg, Sweden, 2014: 860–865.

HU Dezhou, WEI Guanghui, PAN Xiaodong, et al. Investigation of the radiation immunity testing method in reverberation chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(6): 1791–1797 doi: 10.1109/TEMC.2017.2698141

WILSON P F, HILL D A, and HOLLOWAY C L. On Determining the Maximum Emissions From Electrically Large Sources[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 41(1): 79–86.

HILL D A, CAMELL D G, CABCEY K H, et al. Radiated emissions and immunity of microstrip transmission lines: theory and reverberation chamber measurements[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(2): 165–172 doi: 10.1109/15.494619

孙铁雷, 林程, 曹万科. 带有屏蔽线缆的电动车辆动力系统共模模型与预测[J]. 电工技术学报, 2012, 27(2): 128–132

SUN Tielei, LIN Cheng, and CAO Wanke. Common mode prediction oncable shielded drive system in electric vehicle[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 128–132

林福昌, 姚宗干, 代新, 等. 屏蔽电缆共模感应干扰的数值计算方法[J]. 高电压技术, 1997, 23(4): 9–11

LIN Fuchang, YAO Zonggan, DAI Xin, et al. Numerical calculation of common-model interference coupled in a shielded cable[J]. High Voltage Engineering, 1997, 23(4): 9–11

MAGDOWSKI M and VICK R. Closed-form formulas for the stochastic electromagnetic field coupling to a transmission line with arbitrary loads[J]. IEEE Transactions on Electromagnetic Compatibility, 2012, 54(5): 1147–1152 doi: 10.1109/TEMC.2012.2193130

MAGDOWSKI M, TKACHENKO S V, and VICK R. Coupling of stochastic electromagnetic fields to a transmission line in a reverberation chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 2011, 53(2): 308–317 doi: 10.1109/TEMC.2010.2097267

CERRI G, LEO D, MOGLIE F, et al. Theoretical and experimental analysis of the field-to-line coupling in a reverberation chamber[J]. IEEE Proceedings: Science, Measurement and Technology, 2006, 153(6): 201–207 doi: 10.1049/ip-smt:20060014

VUKICEVIC A, RACHIDI F, RUBINSTEIN M, et al. On the evaluation of antenna-mode currents along transmission lines[J]. IEEE Transactions on Electromagnetic Compatibility, 2006, 48(4): 693–700 doi: 10.1109/TEMC.2006.884511

HE Z, ZHA L P, and CHEN R S. Efficient analysis of EM scattering by using higher-order hierarchical linear-liear basis functions[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 305–308 doi: 10.1109/LAWP.2015.2442616

GU Jihong, DING Dazhi, HE Zi, et al. A low frequency EFIE-MLFMA solver based on approximate diagonalization of the Green’s function[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 7150–7156 doi: 10.1109/TAP.2017.2759786

CHEN Shitao, ZHANG Tiancheng, DING Dazhi, et al. EMI analysis of field-line-circuit coupling model based on time domain integral equation method[C]. IEEE Electrical Design Of Advanced Packing & System (EDAPS) Symposium, Hang Zhou, China, 2017.

LUGRIN G, TKACHENKO S V, RACHIDI F, et al. High-Frequency electromagnetic coupling to multiconductor transmission lines of finite length[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(6): 1714–1723 doi: 10.1109/TEMC.2015.2475156

吕琪. 不适定问题的迭代正则化方法研究[D]. [硕士论文], 武汉理工大学, 2012.

LUE Qi. The research of iterative regularization methods for ill-posed[D]. [Master dissertation], Wuhan University of Technology, 2012.

赵占山. 结构故障诊断的几种方法[D]. [硕士论文], 哈尔滨工业大学, 2006.

ZHAO Zhanshan. Several identification method on the structure fault diagnosis[D]. [Master dissertation], Harbin Institute of Technology, 2006.

MENG J, TEO Y X, THOMAS, D W P, et al. Fast prediction of transmission line radiated emissions using the hertzian dipole method and line-end discontinuity models[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(6): 1295–1303 doi: 10.1109/TEMC.2014.2318720

HILL D A. Plane wave integral representation for fields in reverberation chambers[J]. IEEE Transactions on Electromagnetic Compatibility, 1998, 40(3): 209–217 doi: 10.1109/15.709418

施引文献

资源附件(0)

访问统计