Energy Efficient Joint Power Allocation and Beamforming for Cloud Radio Access Network
-
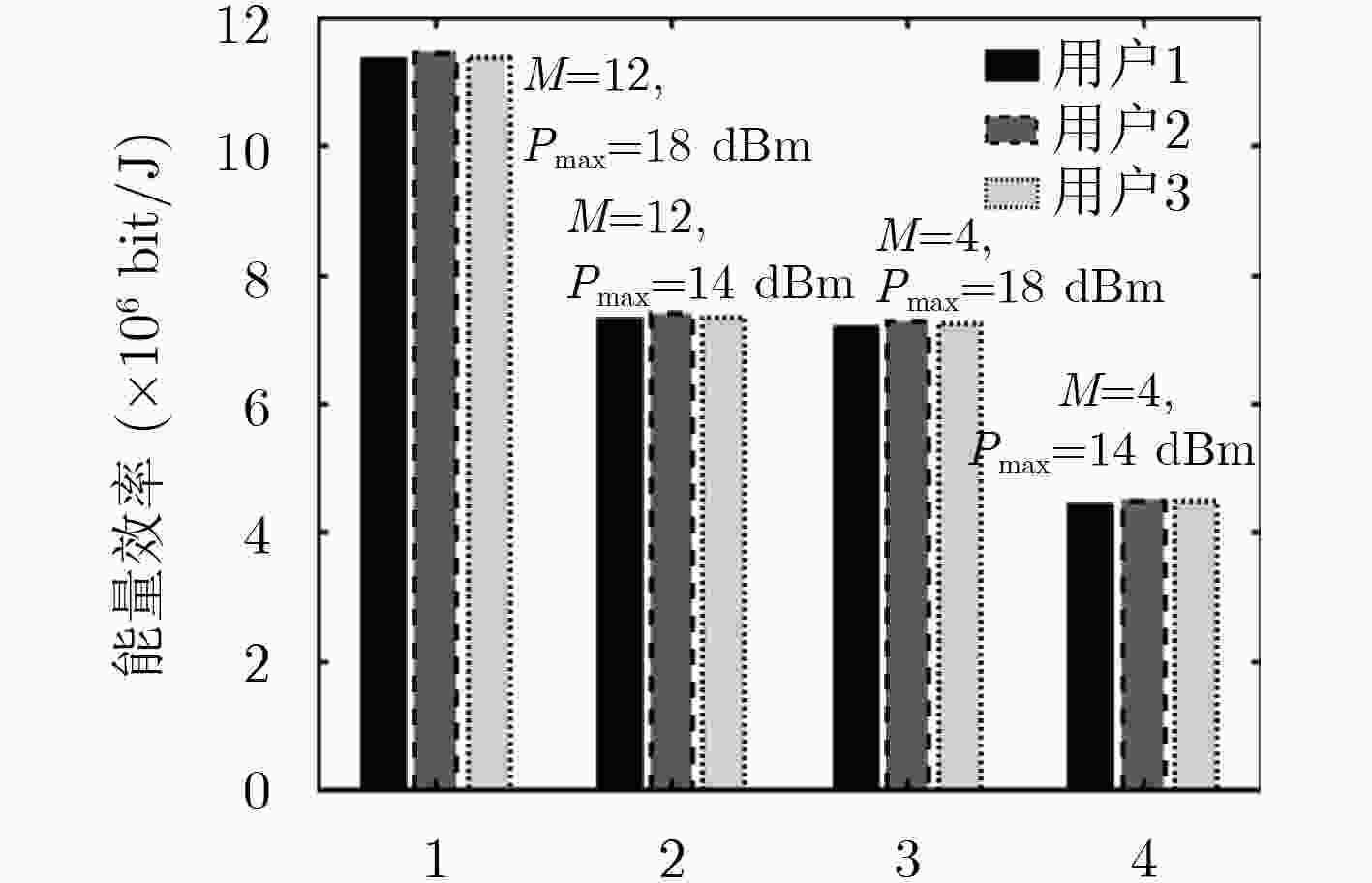
摘要: 针对云无线接入网络(C-RAN)的资源分配问题,该文采用max-min公平准则作为优化准则,以C-RAN用户的能量效率作为优化目标函数,在满足最大发射功率和最小传输速率约束条件下,通过最大化最差链路的能量效率来实现用户发射功率和无线远端射频单元(RRHs)波束成形向量的联合优化。上述优化问题属于非线性、分式规划问题,为了方便求解,首先将原优化问题转化为差分形式的优化问题,然后通过引入变量将差分形式的、非平滑优化问题转化为平滑优化问题。最终,提出一种双层迭代功率分配和波束成形算法。在仿真实验中,将该文算法与传统的非能效资源分配算法和能量效率最大化算法进行了比较,实验结果证明该文算法在改进C-RAN能量效率和提高资源分配公平性方面的有效性。Abstract: The resource allocation for Cloud Radio Access Network (C-RAN) is investigated. The max-min fairness criterion is used as the optimization criterion and the Energy Efficiency (EE) of C-RAN users is taken as the optimization objective function, by maximizing the EE of the worst link under the constraints of maximum transmit power and minimum transmit rate, the user transmit power and Remote Radio Heads (RRHs) beamforming vectors are jointly optimized. The above optimization problem belongs to the nonlinear and fractional programming problem. First, the original nonconvex optimization problem is transformed into an equivalent optimization problem in subtractive form. Then, by introducing a new variable, non-smooth equivalent optimization problem is transformed into a smooth optimization problem. Finally, a two-layer iterative power allocation and beamforming algorithm is proposed. The proposed algorithm is compared with traditional non-EE resource allocation algorithm and EE maximization algorithm. The experimental results show that the proposed algorithm is effective in improving the EE and the fairness of resource allocation.
-
Key words:
- Cloud Radio Access Network (C-RAN) /
- Energy efficiency /
- Power allocation /
- Beamforming
-
表 1 Dinkelbach算法求解优化问题式(6)
外循环: (1)根据式(9)和式(10)计算 $P_{\rm lb}^{\rm{total}}$and $P_{\rm ub}^{\rm{total}}$,令 $t = 1$, ${\mathbb{I}^1} =( - \infty, $
$+\infty)$,选取 ${\lambda ^1} \in {\mathbb{I}^1}$,并设置迭代终止精度阈值 $\varepsilon > 0$(2)对于 ${\lambda ^t}$,通过求解优化问题式(6)得到 ${p_{n,t}}$和 ${{w}_{n,t}}$,n=1,2,···,N (3)计算 $F\left( {{\lambda ^t}} \right) = \mathop {\min }\limits_n \left\{ {{R_n}\left( {{p_{n,t}},{{w}_{n,t}}} \right) - \lambda P_n^{\rm{total}}\left( {{p_{n,t}}} \right)} \right\}$ (4)根据式 (11) 和式 (12)更新区间 $\left[ {\alpha _{\min }^t,\alpha _{\max }^t} \right]$ (5)更新 ${\mathbb{I}^{t + 1}} = {\mathbb{I}^t} \cap \left[ {\alpha _{\min }^t,\alpha _{\max }^t} \right]$,并选取 ${\lambda ^t} \in {\mathbb{I}^{t + 1}}$ (6)如果 $\left| {F\left( {{\lambda ^t}} \right)} \right| \ge \varepsilon $,令 $t = t + 1$ (7)重复步骤2~步骤6,直到 $\left| {F\left( {{\lambda ^t}} \right)} \right| < \varepsilon $ 表 2 求解优化问题式(13)的步骤
内循环: (1)初始化 ${\alpha _n},{\beta _n},{\chi _n}$, ${{w}_{n}}$ (2)repeat (3)根据式(19)更新 ${p_n}$ 由式(21)、式(23)计算 ${\varGamma _n}$和 ${\phi _n}$,根据式(22)计算 ${{w}_{n}}$ (4) $\tau = \tau + 1$, 根据公式(26),式(27),式(28)更新 ${\alpha _n}\left( \tau \right)$, ${\beta _n}\left( \tau \right)$,
${\chi _n}\left( \tau \right)$(5)until ${\alpha _n}\left( {\tau + 1} \right)$, ${\beta _n}\left( {\tau + 1} \right)$, ${\chi _n}\left( {\tau + 1} \right)$收敛 -
ZHANG Deyu, CHEN Zhigang, CAI Lin, et al. Resource allocation for green cloud radio access networks with hybrid energy supplies[J]. IEEE Transactions on Vehicular Technology, 2018, 67(2): 1684–1697 doi: 10.1109/TVT.2017.2754273 DARIO P, ABOLFAZI H, and TUYEN X. Elastic resource utilization framework for high capacity and energy efficiency in cloud RAN[J]. IEEE Communications Magazine, 2016, 54(1): 26–32 doi: 10.1109/MCOM.2016.7378422 SAXENA N, ROY A, and KIM H. Traffic-aware cloud RAN: A key for green 5G networks[J]. IEEE Journal of Selected Areas in Communications, 2016, 34(4): 1010–1021 doi: 10.1109/JSAC.2016.2549438 YOON C and CHO D H. Energy efficient beamforming and power allocation in dynamic TDD based C-RAN system[J]. IEEE Communications Letters, 2015, 19(10): 1806–1809 doi: 10.1109/LCOMM.2015.2469294 LI Peirong and RENG Kaiten. Channel-aware resource allocation for energy-efficient cloud radio access networks under outage specifications[J]. IEEE Transactions on Wireless Communications, 2017, 16(11): 7389–7403 doi: 10.1109/TWC.2017.2748104 ZHAO Zhongyuan, PENG Mugen, DING Zhiguo, et al. Cluster content caching: an energy-efficient approach to improve quality of service in cloud[J]. IEEE Journal of Selected Areas in Communications, 2016, 34(5): 1207–1221 doi: 10.1109/JSAC.2016.2545384 PENG Mugen, WANG Yayun, DANG Tian, et al. Cost-efficient resource allocation in cloud radio access networks with heterogeneous fronthaul expenditures[J]. IEEE Transactions on Wireless Communications, 2017, 16(7): 4626–4638 doi: 10.1109/TWC.2017.2700841 DAI Binbin and YU Wei. Energy efficiency of downlink transmission strategies for cloud radio access networks[J]. IEEE Journal of Selected Areas in Communications, 2016, 34(4): 1037–1050 doi: 10.1109/JSAC.2016.2544459 YANG Jiaxin, CHAMPAGNE B, ZOU Yulong, et al. Centralized energy-efficient multiuser multiantenna relaying in next-generation radio access networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(9): 7913–7924 doi: 10.1109/TVT.2017.2677880 WANG Yong, MA Lin, XU Yubin, et al. Computationally efficient energy optimization for cloud radio access networks with CSI uncertainty[J]. IEEE Transactions on Communications, 2017, 65(12): 1–15 doi: 10.1109/TCOMM.2017.2737014 LI Yuzhou, SHENG Min, TAN W C, et al. Energy-efficient subcarrier assignment and power allocation in OFDM system with max-min fairness guarantees[J]. IEEE Transactions on Communications, 2015, 63(9): 3183–3195 doi: 10.1109/TCOMM.2015.2450724 NGUYEN T D and HAN Y. A proportional fairness algorithm with QoS Provision in downlink OFDM system[J]. IEEE Communications Letters, 2006, 10(11): 760–762 doi: 10.1109/LCOMM.2006.060750 CROUZEIX J P, FERLAND J A, and SCHAIBLE S. Algorithm for generalized fractional programs[J]. Journal of Optimization Theory and Applications, 1985, 47(1): 35–49 doi: 10.1007/BF00941314 CHEN H J, SCHAIBLE S, and SHEN R L. Generic algorithm for generalized fractional programming[J]. Journal of Optimization Theory and Applications, 2009, 141(1): 93–105 doi: 10.1007/s10957-008-9499-7 BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge, England: Cambridge University Press, 2004: 215–223. VENTURINO L, PRASSAD N, and WANG Xiaodong. Coordinated liner beamforming in downlink muti-cell wireless networks[J]. IEEE Transactions on Wierless Communicaitons, 2010, 9(4): 1451–1461 doi: 10.1109/TWC.2010.04.090553 BOYD S, XIAO Lin, and MUTAPCIC A. Subgradient Methods[OL]. http://101.96.10.63/web.mit.edu/6.976/www/notes/subgrad_method.pdf, 2003. PENG Mugen, XIANG Hongyu, Chen Yangyuan, et al. Inter-tier interfernce suppression in heterogeneous cloud radio access networks[J]. IEEE Access, 2015, 3: 2441–2455 doi: 10.1109/ACCESS.2015.2497268 -





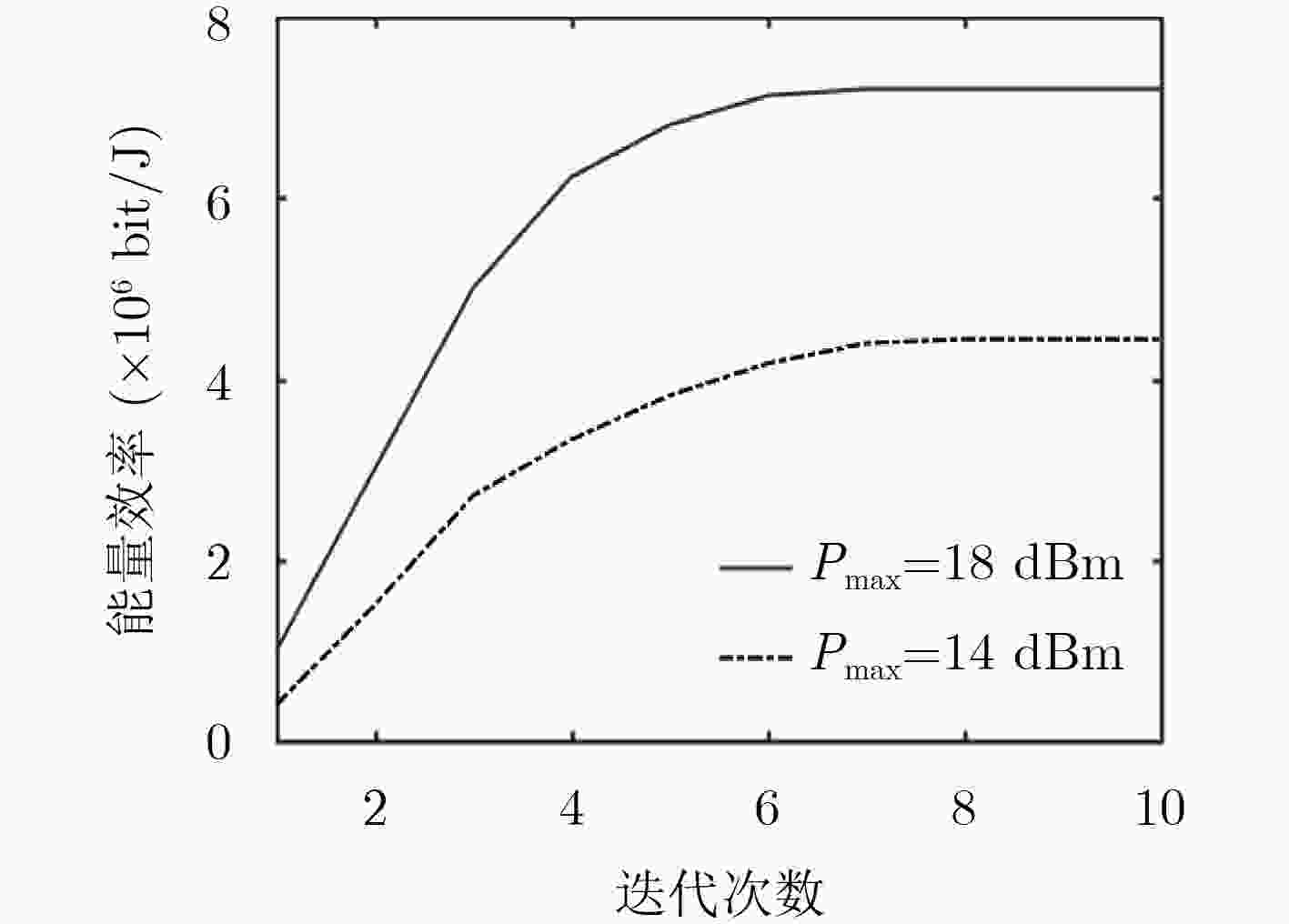
 下载:
下载:
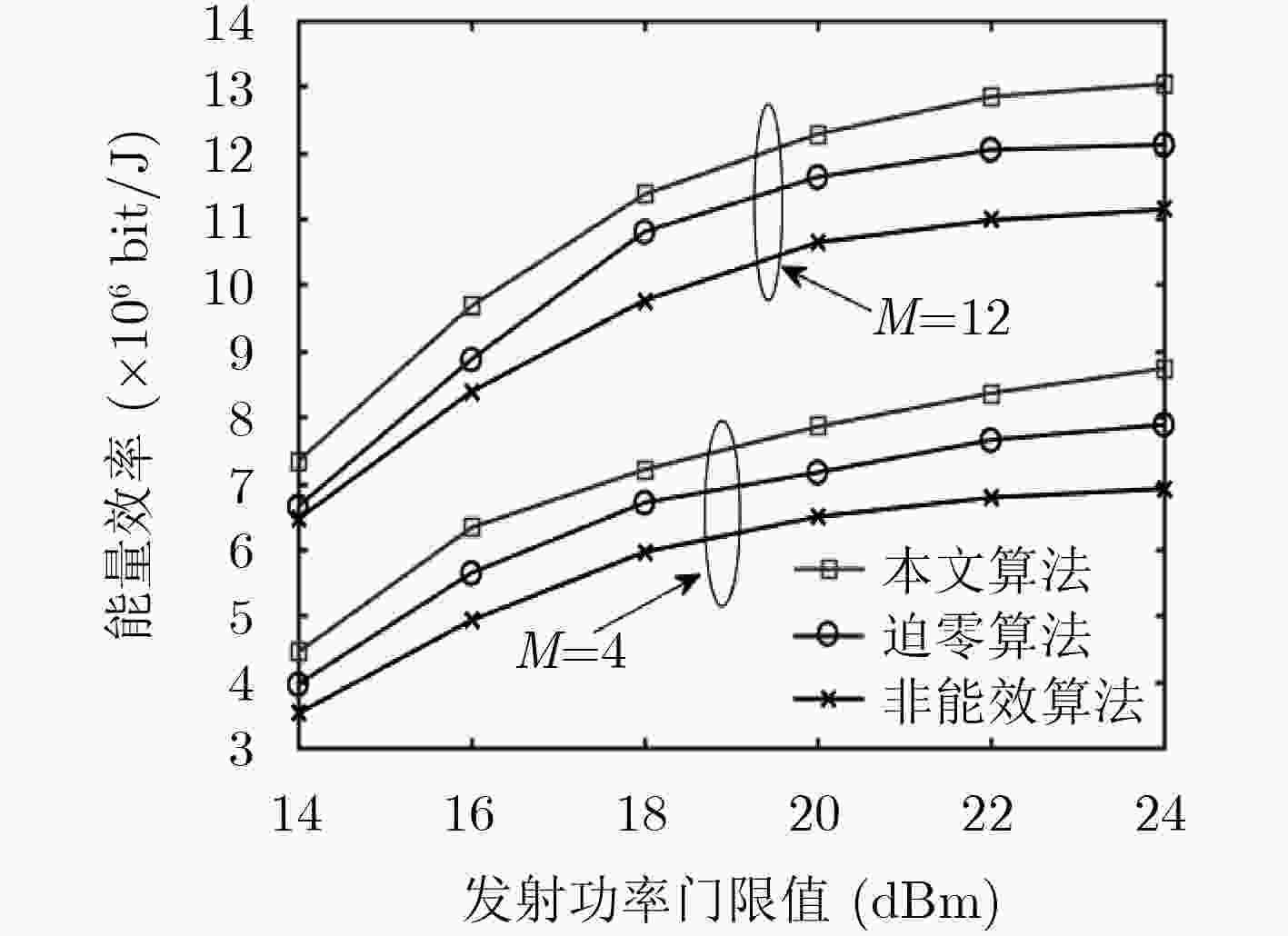
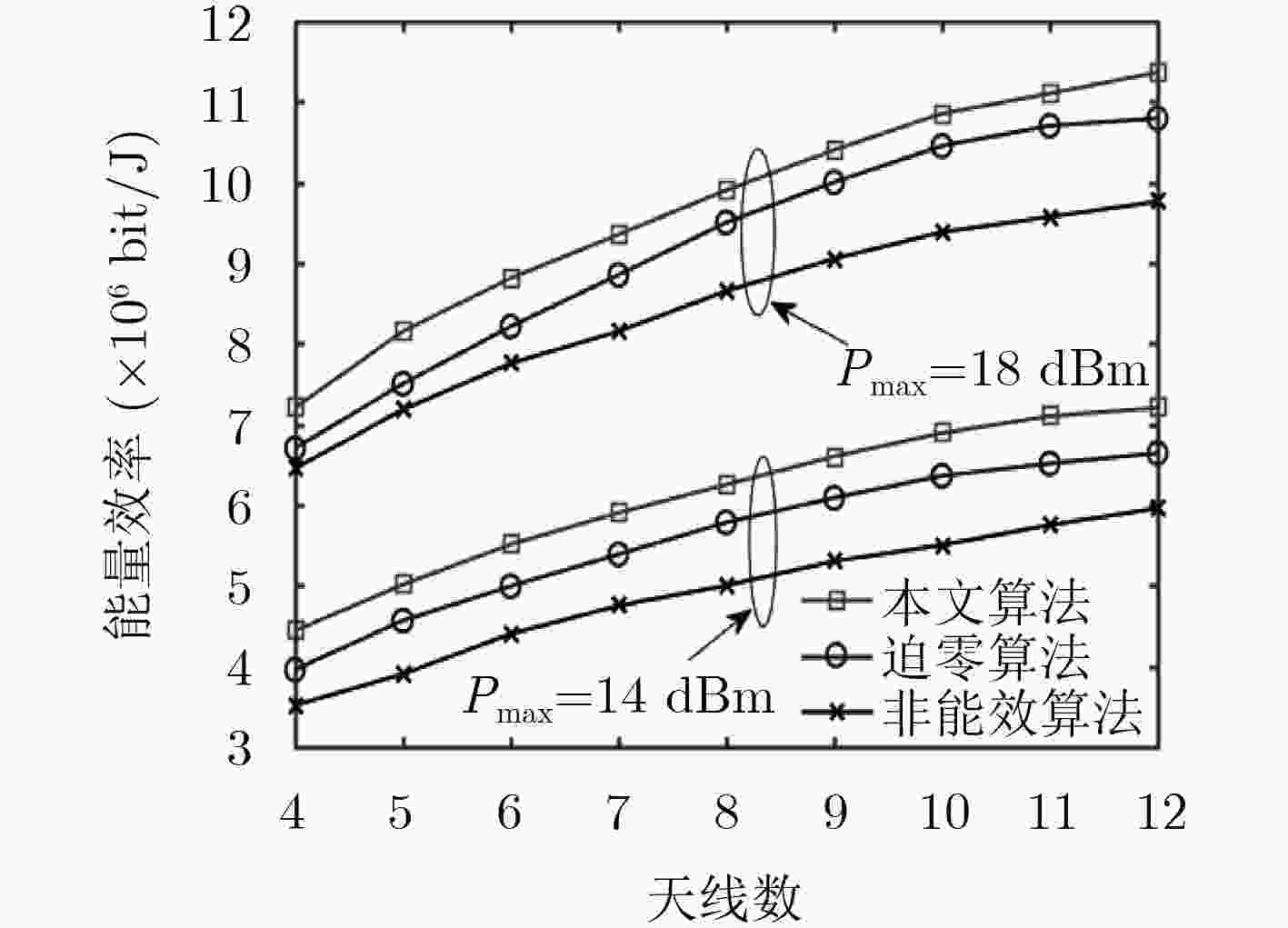
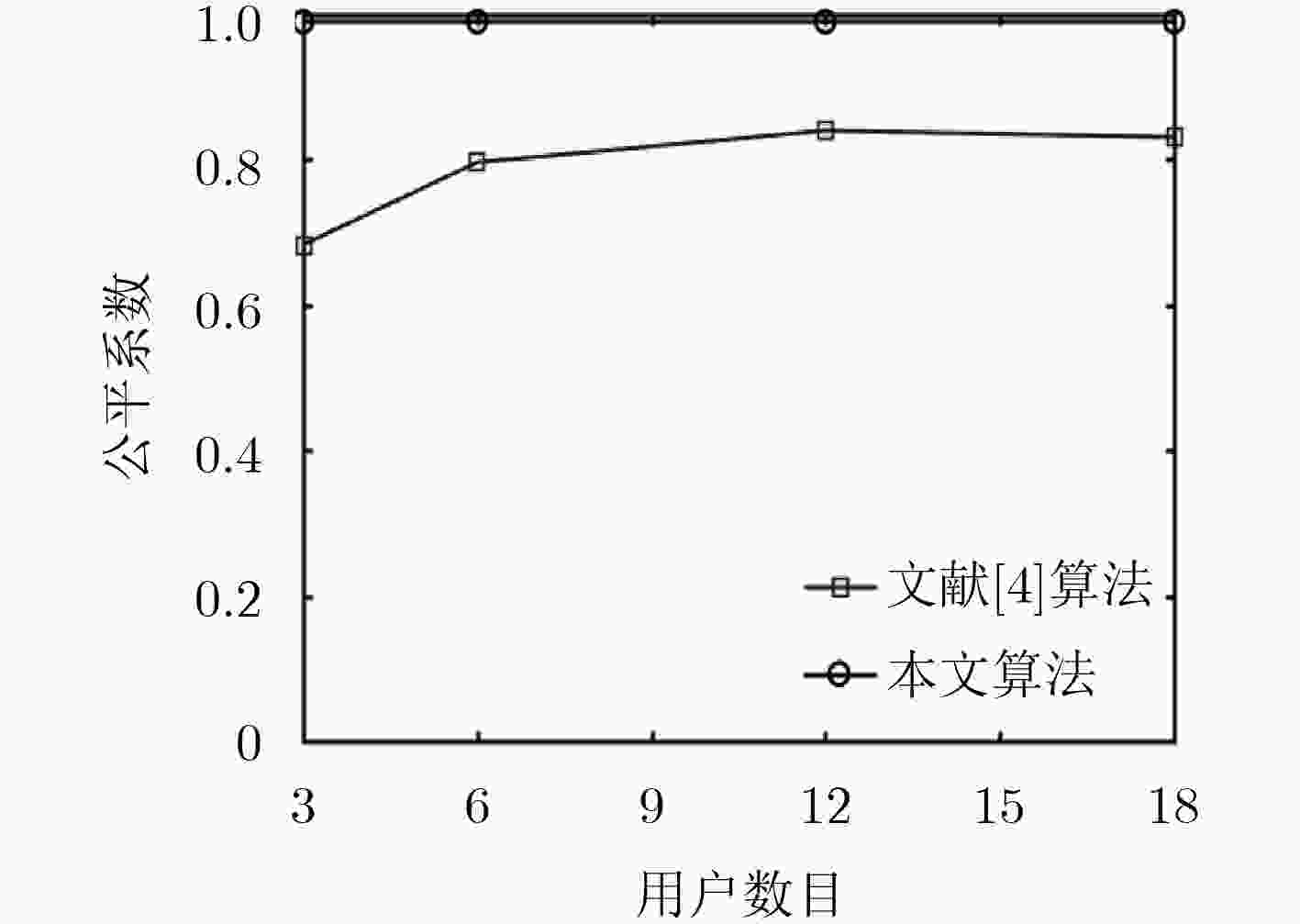


 下载:
下载:
