Improved No-reference Noisy Image Quality Assessment Based on Masking Effect and Gradient Information
-
摘要:
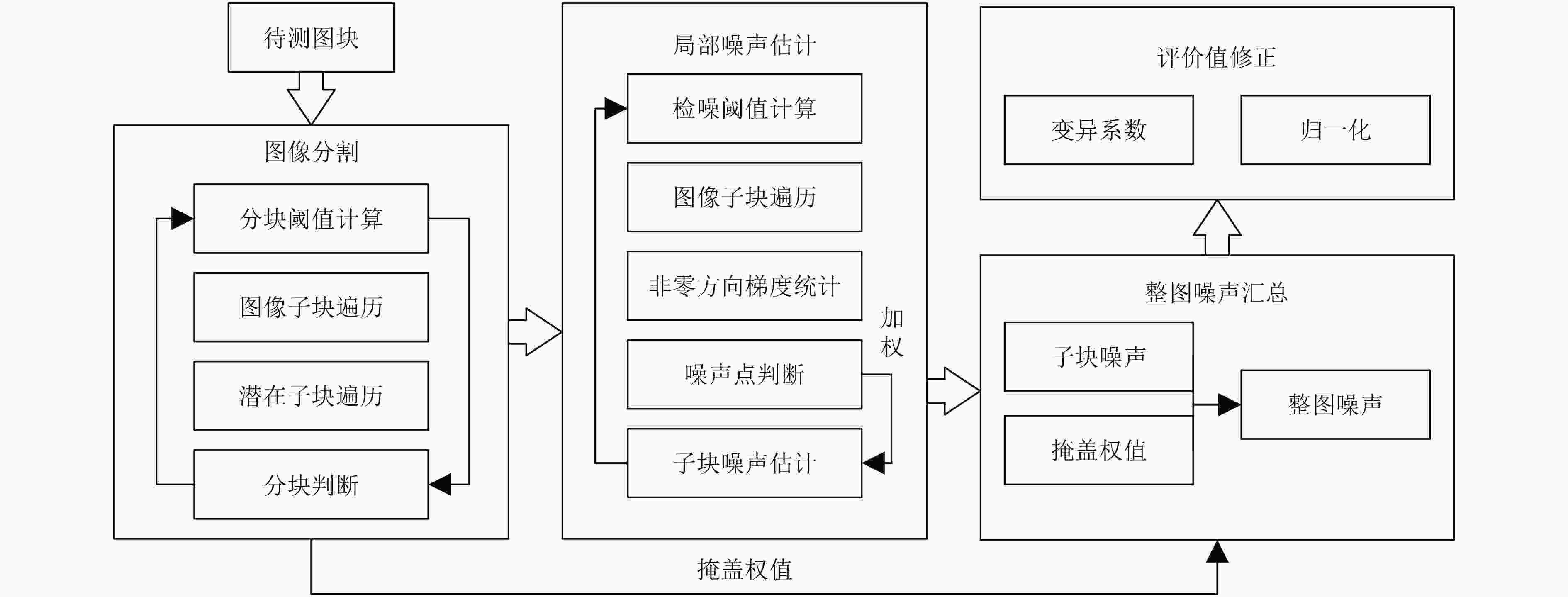
针对目前大多数噪声图像质量评价算法借助域变换或机器学习所带来的运算量大、训练过程繁复等弊端，以及依赖人工设置固定阈值存在普适性不佳的问题，该文改进了一种基于掩盖效应的空域噪声图像质量评价算法。首先依据Hosaka原理提出层递进的分块规则，将图像分成与其内容频率分布高低相符的不同尺寸的子块并赋予相应的掩盖权值；然后通过提取像素点梯度信息，经两步检噪实现子块噪点甄别；再使用掩盖权值对子块噪声污染指标加权得到初步质量评价结果；最终修正和归一化后为整图质量评价结果——改进的无参考峰值信噪比(MNRPSNR)。应用该算法在LIVE和TID2008图像质量评价数据库上对多种噪声类型图像进行实验，结果显示其较目前主流评价算法保有很强竞争力，对传统算法改进效果显著，与人眼主观感受一致性高，普适于多种噪声类型。
Abstract:Heavy computational burden, or complex training procedure and poor universality caused by the manual setting of the fixed thresholds are the main issues associated with most of the noise image quality evaluation algorithms using domain transformation or machine learning. As an attempt for solution, an improved spatial noisy image quality evaluation algorithm based on the masking effect is presented. Firstly, according to the layer-layer progressive rule based on Hosaka principle, an image is divided into sub-blocks with different sizes that match the frequency distribution of its content, and a masking weight is assigned to each sub-block correspondingly. Then the noise in the image is detected through the pixel gradient information extraction, via a two-step strategy. Following that, the preliminary evaluation value is obtained by using the masking weights to weight the noise pollution index of all the sub-blocks. Finally, the correction and normalization are carried out to generate the whole image quality evaluation parameter——i.e. Modified No-Reference Peak Signal to Noise Ratio (MNRPSNR). Such an algorithm is tested on LIVE and TID2008 image quality assessment database, covering a variety of noise types. The results indicate that compared with the current mainstream evaluation algorithms, it has strong competitiveness, and also has the significant effects in improving the traditional algorithm. Moreover, the high degree of consistency to the human subjective feelings and the applicability to multiple noise types are well demonstrated.
-
1. 引言
图像常面临着严峻的噪声干扰，诸多内外因素都可使之在采样、记录、编码、传输、显示等过程中引入噪声，造成失真，严重时甚至丧失使用价值。如能有效衡量出图像中的噪声水平，及早筛选出污染严重的图像，对于提高工程时效意义重大。于是针对噪声图像的质量评价研究日益受到重视。
图像质量评价分为主观质量评价和客观质量评价。主观质量评价主体是人，虽然最为可靠，却固有成本高昂、效率低下、受个体差异影响显著等诸多限制因素。所以目前研究大都集中于客观图像质量评价，即借助相关算法实现评价过程。其中根据参考图像的有无，又可细分为全参考(Full Reference, FR)质量评价[1]、弱参考(Reduced Reference, RR)质量评价[2]和无参考(No Reference, NR)质量评价[3]。由于参考图像大多不易得到或根本无从获取，无参考图像质量评价无疑具有更为广普的意义。
早先噪声图像的质量评价手段主要围绕峰值信噪比(Peak Signal to Noise Ratio, PSNR)展开，但研究表明该指标所得评价结果与人眼主观感受间存在着不容忽视的偏差[4]。近年来以结构相似度[4](Structure SIMilarity, SSIM)的提出作为开端，相关研究逐渐地将人眼视觉系统(Human Visual System, HVS)特征作为构建算法的基石，灵活选择实现手段，如构造视觉码本[5]、离散余弦变换[6–9]、自然场景统计[10–12]、小波变换[10,13,14]、机器学习[15–18]等，涌现出了许多优秀的图像质量评价算法。但这些算法多需借助域变换或机器学习，其中域变换运算量巨大，中间数据沉滞晦涩；而机器学习对模型的建立、训练过程繁复，如BRISQUE算法[17]共需提取18种图像特征，DIIVINE算法[18]更是高达88种，运算耗时惊人。进而不少研究人员选择在空域直接对噪声图像展开质量评价，其中梯度可以有效反映图像纹理、边缘信息，尤其对于孤立噪声点具备相当良好的区分能力[19]，因此受到了颇为广泛的关注。梯度检噪的关键点在于模板算子的设计与检噪阈值的选取。但在现有文献中不乏使用人为设定的常量，如GSM算法[19]需要手动设定梯度算子的尺寸；传统无参考峰值信噪比(No Reference Peak Signal to Noise Ratio, NRPSNR)[20]算法中直接使用固定的分块和检噪阈值，缺乏客观性与普适性。已有文献报道指出重要参数选取得当与否影响算法性能[21]，并验证了不同的模板尺寸对应不同的评价性能[22]。
鉴于此，本文改进基于HVS特性中掩盖效应的传统NRPSNR噪声图像质量评价算法，旨在无需域变换与训练学习的同时，摒弃参数指标的人为设定，从图像自身特征提取分块阈值、检噪阈值等重要参数，以提高评价算法的鲁棒性与普适性，并在国际公认的LIVE和TID2008专业图像质量数据库对该改进算法的性能加以验证。
2. 基于掩盖效应的噪声图像评价基本原理
视觉掩盖效应是人眼视觉系统的一个重要特性，就噪声图像而言人眼容易感知在图像平坦区域的噪声，而对纹理边缘中出现的噪声不敏感[6]。一方面，图像中的纹理边缘和噪声属于高频成分，灰度变化剧烈，相应的像素点灰度值均方差较大，而平坦区域属于低频成分，灰度变化缓慢，其均方差较小。进而结合分块阈值判断，可将图像逐级细分为随频率成分高低而尺寸不同的子块，体现掩盖效应。另一方面，虽然纹理边缘和噪声都属于高频成分，但前者具有明显的结构特征，其与邻域像素存在一定的灰度值约束条件[19,20]。据此结合检噪阈值判断，可将噪声与边缘纹理区分开来。对不同图像块内噪声程度采用不同视觉掩盖权值加权，即频率越高的图像块尺寸越小，对应赋予较小的掩盖权值以弱化噪声刺激；反之频率越低的图像块尺寸越大，赋予更大的掩盖权值突显噪声刺激。最后计算无参考峰值信噪比完成图像质量评价。
3. 改进的噪声图像质量评价算法
图1所示为本文改进算法的主体框架，主要由图像分块与掩盖权值建立、局部噪声估计、整图噪声汇总以及评价值修正等部分构成。
3.1 图像分块
分块方法基于十字等分的Hosaka四叉树分块策略，相较传统NRPSNR算法中人为设置固定分块阈值并与图像块均方差对比进行逐级分块的方法，改进算法结合同级子块像素均方差(MSE)的均值与中值构建分块阈值，逐级自动计算，并将分块规则细化为3条递进判据，由大范围到小局部结合具体图像特征进行判断，多分辨地实现内容频率分布的分析。MSE计算见式(1)，其中M, N分别为图像矩阵I的行、列像素数，
ˉI 为图像块平均灰度值。MSE=M∑i=1N∑j=1(Ii,j−ˉI)2M×N (1) 当某一图像块满足下述分块规则时，认为该图像块中含有较高频率成分内容，有待进一步分块。
对于由同一前级图像块划分而得的4个图像子块，计算其各自均方差并求取均值，记为
¯MSE ，其中均方差大于¯MSE 者继续分块；对于不满足上一条件的图像子块，若其内部所含4个潜在子块中存在均方差大于
¯MSE 者继续分块；计算当前层级所有待分图像块潜在子块的均方差并构成子集，对于不满足上述两个条件的图像块，若其所含子块之均方差存在大于子集中值者继续分块。
具体分块过程：对于读入的图像首先直接等分为4个子块作为第1层分块结果，按照上述规则对当前层级子块遍历判断、加以分块，累加层数并重复这一过程，直到所分子块边长低于8像素。设分块完成后共得到p个图像块，根据尺寸赋予各图像块相应掩盖权值
λ ，见式(2)。其中mk, nk为第k个子块的长和宽。λk=log2(min(mk,nk)) (2) 3.2 局部噪声估计
传统NRPSNR算法中将像素点梯度值与人为设置固定阈值对比以甄别噪声点，本文采用图像中所有像素点梯度的均值Nth作为检噪阈值，以避免人工尝试检噪阈值带来的繁复与主观性。对于任意像素点Ii,j，式(3)给出水平方向梯度hi,j的计算方法，类比计算可得竖直梯度vi,j，正、反对角线梯度di,j, adi,j。
hi,j=||Ii,j+1−Ii,j|+|Ii,j−Ii,j−1|−|Ii,j+1−Ii,j−1|| (3) 取4者中最小值为该像素点梯度值，即
gi,j=min(hi,j,vi,j,di,j,adi,j) (4) 由此可计算出检噪阈值：
Nth=M∑i=1N∑j=1gi,jM×N (5) 具体检噪过程分为两步：
(1)对于任一图像子块，遍历其中像素并逐一计算各点方向梯度，若某一像素点存在两个及以上的非零方向梯度值，则将该像素点归为疑似噪声点；
(2)对于初筛得到的疑似噪声点，若其非零方向梯度值的最小值大于Nth，则确定该点为噪声点。
鉴于孤立性不同的噪点对人眼刺激程度各异，改进算法还使用各噪点非零方向梯度数对其梯度进行加权。设上述方法在一个图像子块中共检测出q个噪声点，梯度值分别为gt(t=1, 2, ···, q)，且对应有Tt(t=1, 2, ···, q)个非零方向梯度值，由式(5)得该图像块噪声污染程度Gk。
Gk=q∑t=1(gt−Nth)Tt2, k=1,2,···,p (6) 3.3 整图噪声汇总
通过汇总各个子块的掩盖权值与噪声污染程度，可以得到整图噪声程度的初步估计结果G，其中M, N为整图行、列像素值：
G=p∑k=1Gk×λkM×N, k=1,2,···,p (7) 结合图像灰度级数l，可求出本文初步评价参数——无参考峰值信噪比(仍沿用NRPSNR名称)：
NRPSNR=10lg(l2/G) (8) 3.4 评价结果修正
改进算法中所有判据、阈值均从图像自身获取，而图像个体信息差异会造成判据、阈值的不同，进而导致初步评价值浮动，故需要对初步结果修正和归一化。检噪主要依据像素梯度信息，在此引入整图像素梯度值的变异系数(Coefficient of Variation, CV)，即所有像素点梯度值的标准差(gsd)与均值(Nth)的比值，加以修正。变异系数以评价特征(梯度值)的数学期望为单位去度量，不仅取决于梯度值的离散程度，还取决于它的平均水平。本文修正在于将噪声强度相同而内容不同图像的评价值映射至统一范围。
gsd=√1M×NM∑i=1N∑j=1(gi,j−Nth)2 (9) 由于Nth即为图像像素点梯度均值，则该图像的变异系数CV易由式(9)得到
CV=gsdNth (10) 结合式(8)—式(10)，进一步利用反正切函数能够将无界数据限制为区间数据的特点实现评价结果归一化，得到最终评价结果——改进的无参考峰值信噪比(Modified No Reference Peak Signal to Noise Ratio, MNRPSNR)。可根据实际情况调整
σ 值以获取所需评价结果分布区间。MNRPSNR=arctan(NRPSNRσ×CV)⋅2×100π (11) 4. 实验结果
本文选用目前权威的公开图像质量评价数据库LIVE[23]和TID2008[24]进行算法测试，具体数据库信息及实验使用子集见表1。其中LIVE数据库侧重于无参考图像质量评价，主观评价结果采取平均评价值(Mean Opinion Score, MOS)，即对图像质量的直接主观评分；TID2008数据库偏重有参考图像质量评价，主观评价结果使用平均评价差值(Difference Mean Opinion Score, DMOS)，即无损图像MOS与待评价图像MOS的差值。较高的MOS值或较低的DMOS值预示着图像具有更佳的主观感受。
表 1 数据库信息及实验使用子集数据库 国家/机构 参考图像数量 主观评价指标 所选失真类型 损伤层级 LIVE 美国/德克萨斯州立大学 29 DMOS 白噪声(WN) 6 TID2008 乌克兰/国家航空航天大学
意大利/罗马大学
芬兰/坦佩雷理工大学25 MOS 加性高斯噪声(AGN) 5 颜色通道加性噪声(ANCC) 空间相关噪声(SCN) 掩蔽噪声(MN) 高频噪声(HFN) 脉冲噪声(IMN) 4.1 对比实验
以LIVE数据库WN子集中的monarch图像组为例，从分块与评价结果两方面对使用固定阈值(按文献[20]取分块阈值300，检噪阈值10, 50, 100)的传统NRPSNR与改进算法进行比对。
图2给出了随噪声方差var渐增而质量下降的一组图像及两种算法的分块结果与数量统计num。对于无噪图像(a1)和噪声污染程度较轻的(a2)、(a3)图像，传统NRPSNR算法和改进算法均能够较好地将图像按照内容频率分布加以分块。但随噪声强度增加图像整体频率提高，NRPSNR算法中使用固定阈值的分块方法对图(a4)至(a6)失效，其将图像皆分为最小尺寸(共得46=4096个子块)；而改进MNRPSNR算法的分块数量基本维持在1600块附近，且分块尺寸与图像频率成分吻合，即便是噪声污染极端严重的图像(a6)改进算法亦能够对其相对频率高低加以区分，较好地体现视觉掩盖效应。
据表2，一方面传统NRPSNR算法对同一幅图像获得的评价参数值随着检噪阈值的增大而显著升高；另一方面对含噪图像的评价效果也因噪声阈值的不同而存在差异：当 Nth取10时评价结果与主观评价结果趋势一致，评价参数值与对应主观评价值变动幅度尚吻合；而Nth取50时对含微量噪声的(a2), (a3)图像相较于无噪图像(a1)的评价值衰减幅度微乎其微，表现为对微量噪声的弱敏感性；当Nth取100时，图2(a2), (a3)的评价值不降反增，与人主观感受完全不符。上述结果充分说明不当的固定阈值可能导致评价效果的下滑甚至失败。相较之下，改进算法在准确反映不同强度噪声对图像主观质量感受影响程度的前提下，对微弱噪声的响应更为敏锐；说明本文阈值设置方法具有更高的自适应性，避免了人为尝试设定阈值带来的盲目与不确定。
表 2 改进算法与不同检噪阈值下传统NRPSNR算法对monarch图像组评价结果DMOS NRPSNR MNRPSNR Nth=10 Nth=50 Nth=100 图2(a1) 0.000000 58.35138 69.74312 79.08684 90.0779 图2(a2) 23.94275 50.45518 69.31391 79.51719 77.9929 图2(a3) 28.44905 47.50428 69.01371 79.70202 76.7756 图2(a4) 41.16959 39.03095 49.28878 65.95135 68.3129 图2(a5) 49.08675 36.47912 43.03078 52.72840 65.3847 图2(a6) 65.73029 33.06348 36.52051 41.17893 60.7793 4.2 开放实验
为全面验证改进算法的综合性能，本文在LIVE和TID2008数据库上，将多种代表性有参考和无参考图像质量评价算法，与传统NRPSNR算法(按文献[20]取分块阈值300、检噪阈值50)及改进算法分别应用于含有不同类型噪声的图像进行质量评价，并选取视频质量专家组(Video Quality Experts Group, VQEG)一份最终报告[25]中推荐的3种指标衡量算法性能：反映算法预测结果准确性的皮尔逊线性相关系数(Pearson Linear Correlation Coefficient, PLCC)、体现主客观评价结果一致性的斯皮尔曼秩相关系数(Spearman Rank Order Correlation Coefficient, SROCC)、度量算法结果无偏性的均方根误差(Root of Mean Squared Error, RMSE)[25]。其中PLCC与SROCC愈接近1、RMSE愈趋近0代表算法性能越佳。
4.2.1 LIVE数据库实验结果
LIVE是近年来图像质量评价领域使用最广的数据库。本文分别选取传统的PSNR算法，较早引入HVS的经典SSIM算法[4]，近年来受到较多关注的VSNR[10], BIQI[26], LBIQ[27], NIQE[28], BRISQUE[17], DIIVINE[18], BLIINDS[8], BLIINDS-II[9]等无参考质量评价算法进行性能指标比对，结果见表3。
表 3 MNRPSNR与相关算法特征及在LIVE数据库测试性能指标算法名称 是否有参考图像 是否需要训练 是否需要域变换 性能指标 PLCC SROCC RMSE PSNR 是 否 否 0.9050 0.9010 8.4500 SSIM 是 否 否 0.9700 0.9690 3.9540 BIQI 否 是 小波 0.9538 0.9510 8.4094 LBIQ 否 是 小波 0.9761 0.9700 7.9100 DIIVINE 否 是 小波 0.9880 0.9840 4.3100 BLIINDS 否 是 离散余弦 0.9140 0.8900 11.2700 BLIINDS-II 否 是 离散余弦 0.9799 0.9691 N/A NIQE 否 是 否 0.9773 0.9662 N/A BRISQUE 否 是 否 0.9851 0.9786 N/A NRPSNR 否 否 否 0.8681 0.8900 10.9133 MNRPSNR 否 否 否 0.9745 0.9813 4.9369 对于PSNR和SSIM两种经典有参考质量评价算法，本文改进算法的表现更为优秀；而对于无参考图像质量评价算法，除却DIIVINE在综合了多达88个图像特征，并经过域变换和训练学习后其3项指标均高于本文算法外，鲜有算法绝对占优，而改进算法的SROCC优于DIIVINE以外的所有算法；PLCC略微逊色于LBIQ, BLIINDS-II, NIQE; RMSE亦控制在相当低的水平。且3项指标均明显优于使用固定阈值的传统NRPSNR算法，说明改进算法在分块与检噪过程中的改进的确更好地起到了拟合人眼视觉特性的作用。由此可见，整体性能相较目前主流无参考图像质量评价算法具备相当的竞争力。
4.2.2 TID2008数据库实验结果
TID2008是目前规模最大、失真类型最丰富的图像质量评价数据库之一，除给出各图像主观评价值外，还提供了诸多全参考图像质量评价算法对应评价结果。本文从中选取VSNR[10], IFC[29], NQM[30], UQI[31]等全参考评价方法，对AWN, ANMC, SCN, MN, HFN以及IMN等类型噪声失真同NRPSNR及改进算法加以性能对比，各指标分别见表4、表5和表6。
表 4 TID2008数据库测试PLCC指标比对VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.7513 0.6147 0.7397 0.5407 0.6467 0.7922 ANCC 0.7489 0.5628 0.6935 0.4930 0.0402 0.7291 SCN 0.7700 0.6567 0.7757 0.5589 0.1624 0.5808 MN 0.7799 0.7309 0.7575 0.7515 0.7903 0.5164 HFN 0.8861 0.7199 0.9134 0.7059 0.9283 0.9005 IMN 0.6244 0.4950 0.7492 0.4829 0.6403 0.8214 表 5 TID2008数据库测试SROCC指标比对VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.7745 0.6204 0.7592 0.5335 0.6276 0.7900 ANCC 0.7725 0.5921 0.7200 0.4798 0.0869 0.7115 SCN 0.7860 0.6403 0.7910 0.5472 0.0491 0.5786 MN 0.7555 0.7374 0.7624 0.7292 0.8018 0.5214 HFN 0.8870 0.7488 0.8952 0.6863 0.9039 0.8852 IMN 0.6460 0.5378 0.7666 0.4951 0.6495 0.8300 表 6 TID2008数据库测试RMSE指标比对VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.4005 0.4783 0.4131 0.5112 0.4682 0.3746 ANCC 0.3646 0.4448 0.3942 0.4844 0.5594 0.3832 SCN 0.3878 0.4655 0.3924 0.5055 0.6134 0.5060 MN 0.3745 0.3844 0.3890 0.3955 0.3673 0.5133 HFN 0.4259 0.6069 0.3691 0.6671 0.3563 0.4161 IMN 0.4022 0.4366 0.3402 0.4483 0.3933 0.2948 全参考评价方法已知原始图像，其评价性能往往优于无参考评价算法。但改进算法在TID2088数据库中性能与VSNR, NQM基本持平，明显好于IFC和UQI，尤其对含有AGN, ANCC, IMN的图像评价效果几乎全面优于其他对比算法。在某些失真类型和指标项上改进算法也仅是略逊于占优指标。同时注意到虽然传统NRPSNR算法对于HFN和MN的评价效果绝对占优，但是对于ANMC与SCN则不具有评价功能，普适程度具有较大局限。但也注意到本文算法对SCN和MN评价效果不够理想，原因在于：
SCN表现形式不是孤立的噪点，因此本文基于梯度的检噪方法有效性受到一定限制。
MN多分布在图像高频区域，对应人眼掩盖效应，图像退化程度较低，算法评价结果普遍较高符合主观感受。但同组各级损伤图像评价值差距缩小，组间差异相对明显。
4.3 运行时间对比
选取在LIVE数据库上某些指标项略优于本文算法的DIIVINE[18]与BLIINDS-II[9]算法以及原始NRPSNR算法进行单张图像平均处理时长的比较，如表7所示。
表 7 MNRPSNR与相关算法在LIVE数据库上运行时间(s)算法名称 DIIVINE BLIINDS-II NRPSNR MNRPSNR 平均单幅耗时 149 70 3.45 10.10 DIIVINE与BLIINDS-II两种机器算法虽然在PLCC或SROCC指标项上略优，但由于涉及域变换和大量特征项的提取，耗时过长；改进算法相较NRPSNR在分块与检噪等方面做出诸多改进，尤其对分块计算过程，使用了递进的双重判据，耗时有所增加，但换取了评价性能的大幅提高。
5. 结束语
本文针对传统NRPSNR算法存在的不足，提出了一种噪声图像质量评价改进算法。该算法结合视觉掩盖效应和Hosaka方法，通过挖掘图像自身特征，逐级自动调整分块与检噪阈值，并进一步完善相关判据策略，加入对评价参数的修正与归一化处理，获得了改进的评价参数值。相较传统NRPSNR算法，改进算法在分块合理性与检噪准确性方面明显提高，整体评价性能更优，与人眼主观感受间保持了高度一致性。通过在LIVE和TID2008数据库上进行测试，结果表明本文算法能够有效评价多种类型噪声失真，综合性能与主流评价算法相当甚至占优，且在算法实现上更为简单便捷。课题后续研究将着力对性能指标有待提高的噪声类型补足完善，并对噪声外其他类型失真评价加以探索。
-
表 1 数据库信息及实验使用子集
数据库 国家/机构 参考图像数量 主观评价指标 所选失真类型 损伤层级 LIVE 美国/德克萨斯州立大学 29 DMOS 白噪声(WN) 6 TID2008 乌克兰/国家航空航天大学
意大利/罗马大学
芬兰/坦佩雷理工大学25 MOS 加性高斯噪声(AGN) 5 颜色通道加性噪声(ANCC) 空间相关噪声(SCN) 掩蔽噪声(MN) 高频噪声(HFN) 脉冲噪声(IMN) 
下载: 导出CSV
表 2 改进算法与不同检噪阈值下传统NRPSNR算法对monarch图像组评价结果
DMOS NRPSNR MNRPSNR Nth=10 Nth=50 Nth=100 图2(a1) 0.000000 58.35138 69.74312 79.08684 90.0779 图2(a2) 23.94275 50.45518 69.31391 79.51719 77.9929 图2(a3) 28.44905 47.50428 69.01371 79.70202 76.7756 图2(a4) 41.16959 39.03095 49.28878 65.95135 68.3129 图2(a5) 49.08675 36.47912 43.03078 52.72840 65.3847 图2(a6) 65.73029 33.06348 36.52051 41.17893 60.7793
下载: 导出CSV
表 3 MNRPSNR与相关算法特征及在LIVE数据库测试性能指标
算法名称 是否有参考图像 是否需要训练 是否需要域变换 性能指标 PLCC SROCC RMSE PSNR 是 否 否 0.9050 0.9010 8.4500 SSIM 是 否 否 0.9700 0.9690 3.9540 BIQI 否 是 小波 0.9538 0.9510 8.4094 LBIQ 否 是 小波 0.9761 0.9700 7.9100 DIIVINE 否 是 小波 0.9880 0.9840 4.3100 BLIINDS 否 是 离散余弦 0.9140 0.8900 11.2700 BLIINDS-II 否 是 离散余弦 0.9799 0.9691 N/A NIQE 否 是 否 0.9773 0.9662 N/A BRISQUE 否 是 否 0.9851 0.9786 N/A NRPSNR 否 否 否 0.8681 0.8900 10.9133 MNRPSNR 否 否 否 0.9745 0.9813 4.9369
下载: 导出CSV
表 4 TID2008数据库测试PLCC指标比对
VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.7513 0.6147 0.7397 0.5407 0.6467 0.7922 ANCC 0.7489 0.5628 0.6935 0.4930 0.0402 0.7291 SCN 0.7700 0.6567 0.7757 0.5589 0.1624 0.5808 MN 0.7799 0.7309 0.7575 0.7515 0.7903 0.5164 HFN 0.8861 0.7199 0.9134 0.7059 0.9283 0.9005 IMN 0.6244 0.4950 0.7492 0.4829 0.6403 0.8214
下载: 导出CSV
表 5 TID2008数据库测试SROCC指标比对
VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.7745 0.6204 0.7592 0.5335 0.6276 0.7900 ANCC 0.7725 0.5921 0.7200 0.4798 0.0869 0.7115 SCN 0.7860 0.6403 0.7910 0.5472 0.0491 0.5786 MN 0.7555 0.7374 0.7624 0.7292 0.8018 0.5214 HFN 0.8870 0.7488 0.8952 0.6863 0.9039 0.8852 IMN 0.6460 0.5378 0.7666 0.4951 0.6495 0.8300
下载: 导出CSV
表 6 TID2008数据库测试RMSE指标比对
VSNR IFC NQM UQI NRPSNR MNRPSNR AGN 0.4005 0.4783 0.4131 0.5112 0.4682 0.3746 ANCC 0.3646 0.4448 0.3942 0.4844 0.5594 0.3832 SCN 0.3878 0.4655 0.3924 0.5055 0.6134 0.5060 MN 0.3745 0.3844 0.3890 0.3955 0.3673 0.5133 HFN 0.4259 0.6069 0.3691 0.6671 0.3563 0.4161 IMN 0.4022 0.4366 0.3402 0.4483 0.3933 0.2948
下载: 导出CSV
-
HADIZADEH H and VAN BAJIC I. Full-reference objective quality assessment of tone-mapped images[J]. IEEE Transactions on Multimedia, 2018, 20(2): 392–404. doi: 10.1109/TMM.2017.2740023 MA Jian, AN Ping, SHEN Liquan, et al. Reduced-reference stereoscopic image quality assessment using natural scene statistics and structural degradation[J]. IEEE Access, 2018, 6: 2768–2780. doi: 10.1109/ACCESS.2017.2785282 FANG Yuming, YAN Jiebin, LI Leida, et al. No reference quality assessment for screen content images with both local and global feature representation[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1600–1610. doi: 10.1109/TIP.2017.2781307 WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861 YE Peng and DAVID D. No-reference image quality assessment based on visual codebook[C]. IEEE International Conference on Image Processing, Brussels, Belgium 2011: 11–14. WAN Wenfei, WU Jinjian, XIE Xuemei, et al. A novel just noticeable difference model via orientation regularity in DCT domain[J]. IEEE Access, 2017, 5: 22953–22964. doi: 10.1109/ACCESS.2017.2699858 MA Lin, WANG Xu, LIU Qiong, et al. Reorganized DCT-based image representation for reduced reference stereoscopic image quality assessment[J]. Neurocomputing, 2016, 215: 21–31. doi: 10.1016/j.neucom.2015.06.116 SAAD M A, BOVIK A C, and CHARRIER C. A DCT statistics-based blind image quality index[J]. IEEE Signal Processing Letters, 2010, 17(6): 583–586. doi: 10.1109/LSP.2010.2045550 SAAD M A, BOVIK A C, and CHARRIER C. Blind image quality assessment: A natural scene statistics approach in the DCT domain[J]. IEEE Transactions on Image Processing, 2012, 22(8): 3339–3352. doi: 10.1109/TIP.2012.2191563 CHANDLER D M and HEMAMI S S. VSNR: A wavelet-based visual signal-to-noise ratio for natural images[J]. IEEE Transactions on Image Processing, 2007, 16(9): 2284–2298. doi: 10.1109/TIP.2007.901820 QIN Ming, LÜ Xiaoxin, CHEN Xiaohui, et al. Hybrid NSS features for no-reference image quality assessment[J]. IET Image Processing, 2017, 11(6): 443–449. doi: 10.1049/iet-ipr.2016.0411 LI Leida, YAN Ya, LU Zhaolin, et al. No-reference quality assessment of deblurred images based on natural scene statistics[J]. IEEE Access, 2017, 5: 2163–2171. doi: 10.1109/ACCESS.2017.2661858 YANG Guangyi, LIAO Yue, ZHANG Qingyi, et al. No-reference quality assessment of noise-distorted images based on frequency mapping[J]. IEEE Access, 2017, 5: 23146–23156. doi: 10.1109/ACCESS.2017.2764126 ABDEL-HAMID L, EI-RAFEI A, and MICHELSON G. No-reference quality index for color retinal images[J]. Computers in Biology and Medicine, 2017, 90: 68–75. doi: 10.1016/j.compbiomed.2017.09.012 MA Kede, LIU Wentao, ZHANG Kai, et al. End-to-end blind image quality assessment using deep neural networks[J]. IEEE Transactions on Image Processing, 2018, 27(3): 1202–1213. doi: 10.1109/TIP.2017.2774045 LIU Tsungjung and LIU Kuanhsien. No-reference image quality assessment by wide-perceptual-domain scorer ensemble method[J]. IEEE Transaction on Image Processing, 2018, 27(3): 1138–1151. doi: 10.1109/TIP.2017.2771422 MITTAL A, MOORTHY A K, and BOVIK A C. No-reference image quality assessment in the spatial domain[J]. IEEE Transactions on Image Processing, 2012, 21(12): 4659–4708. doi: 10.1109/TIP.2012.2214050 MOORTHY A K and BOVIK A C. Blind image quality assessment: From natural scene statistics to perceptual quality[J]. IEEE Transactions on Image Processing, 2011, 20(12): 3350–3364. doi: 10.1109/TIP.2011.2147325 LIU Anmin and LIN Weisi. Image quality assessment based on gradient similarity[J]. IEEE Transactions on Image Processing, 2012, 21(4): 1500–1512. doi: 10.1109/TIP.2011.2175935 王正友, 肖文. 基于掩盖效应的无参考数字图像质量评价[J]. 计算机应用, 2006, 26(12): 2838–2840.WANG Zhengyou and XIAO Wen. No-reference digital image quality evaluation based on perceptual masking[J]. Computer Applications, 2006, 26(12): 2838–2840. 徐海勇, 郁梅, 骆挺, 等. 基于非负矩阵分解的彩色图像质量评价方法[J]. 电子与信息学报, 2016, 38(3): 578–585. doi: 10.11999/JEIT150610XU Haiyong, YU Mei, LUO Ting, et al. A color image quality assessment method based on non-negative matrix factorization[J]. Journal of Electronics &Information Technology, 2016, 38(3): 578–585. doi: 10.11999/JEIT150610 蒋平, 张建州. 基于局部最大梯度的无参考图像质量评价[J]. 电子与信息学报, 2015, 37(11): 2587–2593. doi: 10.11999/JEIT141447JIANG Ping and ZHANG Jianzhou. No-reference image quality assessment based on local maximum gradient[J]. Journal of Electronics &Information Technology, 2015, 37(11): 2587–2593. doi: 10.11999/JEIT141447 SHEIKH H R, WANG Zhou, and CORMACK L. LIVE image quality assessment database, release 2 [EB/OL]. http://live.ece.utexass.edu/research/quality, 2005. PONOMARENKO N. Tampere image database 2008 TID2008, version 1.0[EB/OL]. http://www.ponomarenko.info/index.html, 2009. Final Report from the Video Quality Experts Group on the Validation of Objective Models of Video Quality Assessment, Phase II VQEG [OL]. http://www.vqeg.org/, 2003. MOORTHY A K and BOVIK A C. A two-step framework for constructing blind image quality indices[J]. IEEE Signal Processing Letters, 2010, 17(5): 513–516. doi: 10.1109/LSP.2010.2043888 TANG Huixuan, JOSHI N, and KAPOOR A. Learning a blind measure of perceptual image quality[C]. IEEE Conference on Computer Vision and Pattern Recognition, Colorado, USA, 2011: 305–312. MITTAL A, SOUNDARARAJAN R, and BOVIK A C. Making a " completely blind” image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209–212. doi: 10.1109/LSP.2012.2227726 SHEIKH H R, BOVIK A C, and DE VECIANA G. An information fidelity criterion for image quality assessment using natural scene statistics[J]. IEEE Transactions on Image Processing, 2005, 14(12): 2117–2128. doi: 10.1109/TIP.2005.859389 DAMERA-VENKATA N, KITE T D, GEISLER W S, et al. Image quality assessment based on a degradation model[J]. IEEE Transactions on Image Processing, 2000, 9(4): 636–650. doi: 10.1109/83.841940 WANG Zhou and BOVIK A C. A universal image quality index[J]. IEEE Signal Processing Letters, 2002, 9(3): 81–84. doi: 10.1109/97.995823 期刊类型引用(4)
1. 彭晏飞，王静，刘晓轩，巩胜杰. 结合主成分分析和图像分块的重定向研究. 液晶与显示. 2024(02): 157-167 . 
百度学术2. 崔嘉，宋磊，陆宏菊，唐明晰，戚萌. 基于最小位移可视差的连续Seam Carving算法在图像缩放中的研究. 电子与信息学报. 2021(04): 1014-1021 . 
本站查看3. 张雅茹. 基于DCT的无参考JPEG压缩图像质量评价研究. 太原学院学报(自然科学版). 2021(03): 66-70 . 百度学术4. 王怡影，章承诺，徐静静，范程华，柴豆豆. 基于掩盖模型非线性变换的相关性分析. 蚌埠学院学报. 2020(05): 53-56 . 百度学术其他类型引用(7)
-
下载:
百度学术
计量
- 文章访问数: 1441
- HTML全文浏览量: 711
- PDF下载量: 75
- 被引次数: 11
下载:
