Gain and Phase Calibration Algorithm of Near-field Source Based on Instrumental Sensors
-
摘要: 针对近场源的定位及阵列幅相误差校正问题,该文提出一种基于均匀对称阵列利用辅助阵元矢量重构解耦合的幅相误差校正方法。通过重构虚拟阵列实现距离参数的分离,再通过对虚拟阵列导向矢量的变换实现方位和幅相误差之间的解耦合;最后通过对实阵列导向矢量的变换,实现距离与幅相误差的解耦合,从而实现对近场源的方位角、距离以及阵列的幅相误差系数的级联估计。仿真结果表明所提算法相比现有算法运算量小,方位及距离参数估计精确,幅相误差校正精度高。Abstract: In order to solve the problem of near-field source localization and array gain-phase error calibration, a method of gain-phase error calibration is proposed based on uniform array symmetry. The distance parameter is separated by reconstructing the virtual array, and then the decoupling between azimuth and error is realized by transforming the steering vector of the virtual array. Through the transformation of the real array steering vector, the decoupling between the distance and the gain-phase error is realized, and the cascade estimation of the azimuth and distance of the near-field source and the gain-phase error coefficient of the array is achieved. The simulation results show that compared with the exist algorithms, the proposed algorithm has less computational complexity, more accurate azimuth and distance parameters estimation, and higher accuracy of gain and phase error calibration.
-
表 1 各个通道误差系数的真实值、估计值以及差值
误差系数 阵元2 阵元3 阵元4 阵元5 真实值 1.0000+0.0000i 0.9822–0.0181i 0.9909–0.0688i 0.9889+0.0162i 估计值 1.0000+0.0000i 0.9820–0.0183i 0.9908–0.0686i 0.9885+0.0142i 差值的绝对值 0.0000+0.0000i 0.0003+0.0000i 0.0002+0.0000i 0.0020+0.0000i 误差系数 阵元6 阵元7 阵元8 阵元9 真实值 1.0167+0.0121i 0.9820+0.0447i 1.0068+0.0062i 1.0077+0.0573i 估计值 1.0153+0.0103i 0.9817+0.0442i 1.0050+0.0060i 1.0081+0.0564i 差值的绝对值 0.0022+0.0000i 0.0005+0.0000i 0.0019+0.0000i 0.0010+0.0000i 误差系数 阵元10 阵元11 阵元12 真实值 1.0103–0.0410i 0.9976–0.0580i 1.0000+0.0000i 估计值 1.0105–0.0402i 0.9973–0.0575i 0.9999–0.0007i 差值的绝对值 0.0008+0.0000i 0.0006+0.0000i 0.0007+0.0000i -
SWINDLEHURST A L and KAILATH T. Passive direction of arrival and range estimation for near-field sources[C]. IEEE Spectrum Estimation and Modeling Workshop, MN, USA, 1988: 123–128. LI Jianzhong, WEI Gang, and MA Biyun. A simple way of near-field source localization with MUSIC[C]. IEEE International Conference on Computational Electromagnetics, Guangzhou, China, 2016: 330–332. XIE Jian, TAO Haihong, RAO Xuan, et al. Localization of mixed far-field and near-field sources under unknown mutual coupling[J]. Digital Signal Processing, 2016, 50(C): 229–239 doi: 10.1016/j.dsp.2015.10.012 SINGH P R, WANG Y, and CHARGE P. Near field targets localization using bistatic MIMO system with symmetric arrays[C]. IEEE Signal Processing Conference, Kos, Greece, 2017: 2408–2412. 陈建峰, 张贤达, 吴云韬. 近场源距离、频率及到达角联合估计算法[J]. 电子学报, 2004, 32(5): 803–806 doi: 10.3321/j.issn:0372-2112.2004.05.023CHEN Jianfeng, ZHANG Xianda, and WU Yuntao. An algorithm for jointly estimating range, DOA and frequency of near field source[J]. Acta Electronica Sinica, 2004, 32(5): 803–806 doi: 10.3321/j.issn:0372-2112.2004.05.023 黄家才, 石要武, 陶建武. 一种新的近场源距离及到达角联合估计算法[J]. 电子与信息学报, 2007, 29(11): 2738–2742 doi: 10.3724/SP.J.1146.2006.00633HUANG Jiacai, SHI Yaowu, and TAO Jianwu. A new method for range and DOA estimation of near-field sources[J]. Journal of Electronics&Information Technology, 2007, 29(11): 2738–2742 doi: 10.3724/SP.J.1146.2006.00633 CHEN Xin, LIN Zhen, and WEI Xizhang. Unambiguous parameter estimation of multiple near-field sources via totating uniform circular array[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 872–875 doi: 10.1109/LAWP.2016.2613084 KIM Jungtai, YANG Hyunjong, JUNG Byungwook, et al. Blind calibration for a linear array with gain and phase error using independent component analysis[J]. IEEE Antennas and Wireless Letters, 2010, 9(10): 1259–1262 doi: 10.1109/LAWP.2010.2104132 LIU Hongqing, ZHAO Luming, LI Yong, et al. A sparse-based approach for DOA estimation and array calibration in uniform linear array[J]. IEEE Sensors Journal, 2016, 16(15): 6018–6027 doi: 10.1109/JSEN.2016.2577712 LI Youming and ER M H. Theoretical analyses of gain and phase error calibration with optimal implementation for linear equispaced array[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 712–723 doi: 10.1109/TSP.2005.861892 程丰, 龚子平, 张驰, 等. 一种基于旋转测量的阵列幅相误差校正新方法[J]. 电子与信息学报, 2017, 39(8): 1899–1905 doi: 10.11999/JEIT161058CHENG Feng, GONG Ziping, ZHANG Chi, et al. A new rotation measurement-based method for array gain-phase errors calibration[J]. Journal of Electronics&Information Technology, 2017, 39(8): 1899–1905 doi: 10.11999/JEIT161058 王布宏, 王永良, 陈辉, 等. 方位依赖阵元幅相误差校正的辅助阵元法[J]. 中国科学E辑: 信息科学, 2004, 34(8): 906–918 doi: 10.3321/j.issn:1006-9275.2004.08.006WANG Buhong, WANG Yongliang, CHEN Hui, et al. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J]. Science in China Ser. E Information Sciences, 2004, 34(8): 906–918 doi: 10.3321/j.issn:1006-9275.2004.08.006 芦迅, 甄佳奇. 基于幅相误差阵列的远近场混合信号超分辨测向方法[J]. 电波科学学报, 2017, 32(2): 227–236 doi: 10.13443/j.cjors.2016120401LU Xun and ZHEN Jiaqi. Super-resolution direction finding method for mixed far-field and near-field signals based on gain-phase error array[J]. Chinese Journal of Radio Science, 2017, 32(2): 227–236 doi: 10.13443/j.cjors.2016120401 DAI Zheng, SU Weimin, GU Hong, et al. Sensor gain-phase errors estimation using disjoint sources in unknown directions[J]. IEEE Sensors Journal, 2016, 16(10): 3724–3730 doi: 10.1109/JSEN.2016.2531282 付永庆, 郑莉, 邵学辉. 一种监听键盘录入信息的新方法[J]. 哈尔滨工程大学学报, 2008, 29(2): 175–178 doi: 10.3969/j.issn.1006-7043.2008.02.014FU Yongqing, ZHENG Li, and SHAO Xuehui. Intercepting messages using the sounds of keystrokes[J]. Journal of Harbin Engineering University, 2008, 29(2): 175–178 doi: 10.3969/j.issn.1006-7043.2008.02.014 -





 下载:
下载:

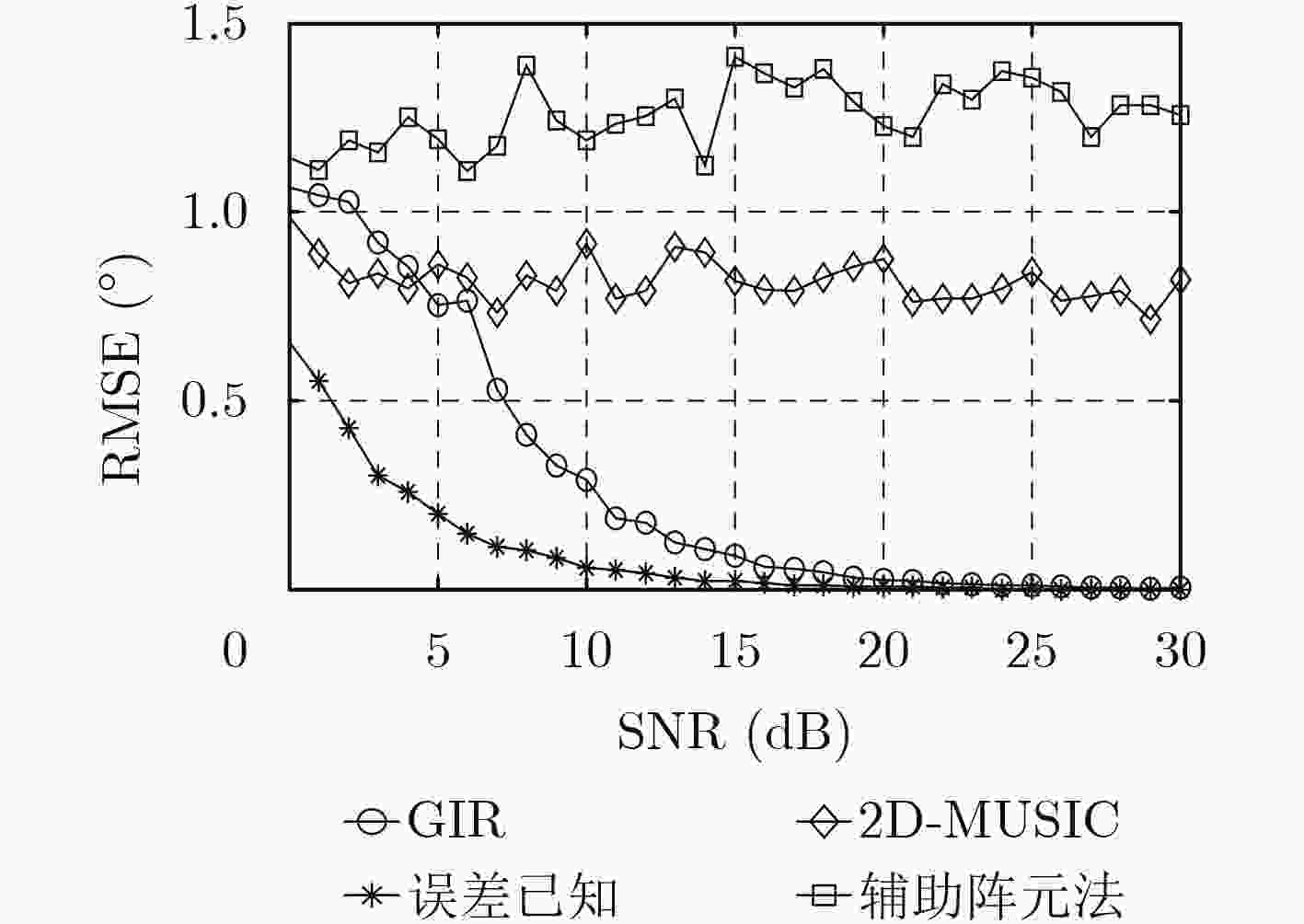
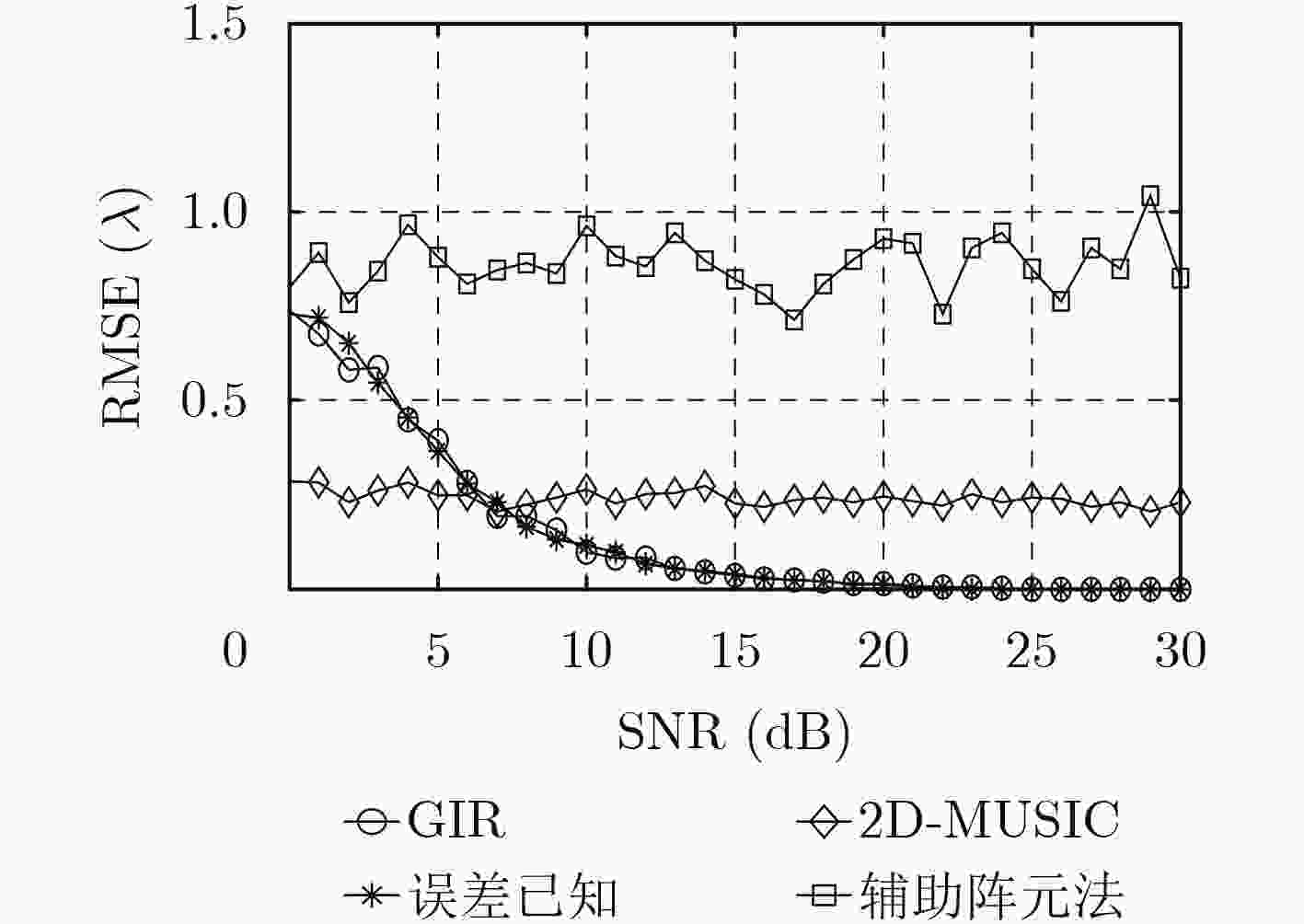


 下载:
下载:
