融合射频识别和激光信息的动态目标定位

刘冉; 梁高丽; 王姮; 付余路; 何静; 张华

doi:10.11999/JEIT171088

融合射频识别和激光信息的动态目标定位

doi: 10.11999/JEIT171088

西南科技大学信息工程学院绵阳 621010

基金项目: 国家自然科学基金(61601381, 61701421, 61471306)，国家核能开发项目([2016]1295)

详细信息

作者简介:
刘冉：男，1986年生，博士，副研究员，研究方向为智能机器人、多传感器信息融合、室内定位

梁高丽：女，1992年生，硕士生，研究方向为RFID导航、机器人控制

王姮：女，1971年生，教授，研究方向为机器人技术及应用、机器学习

付余路：女，1991年生，硕士生，研究方向为RFID定位、智能信号处理

何静：男，1994年生，硕士生，研究方向为机器人导航与定位、智能控制技术

张华：男，1969年生，教授，研究方向为人工智能、模式识别与智能系统

通讯作者:
刘冉　 ran.liu.86@hotmail.com

中图分类号: TP301.6
计量
- 文章访问数: 1655
- HTML全文浏览量: 559
- PDF下载量: 62
- 被引次数: 2
出版历程
- 收稿日期: 2017-11-20
- 修回日期: 2018-08-21
- 网络出版日期: 2018-08-28
- 刊出日期: 2018-11-01

Dynamic Object Localization Based on Radio Frequency Identification and Laser Information

School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China

Funds: The National Natural Science Foundation of China (61601381, 61701421, 61471306), The National Nuclear Energy Development Program of China ([2016]1295)

摘要

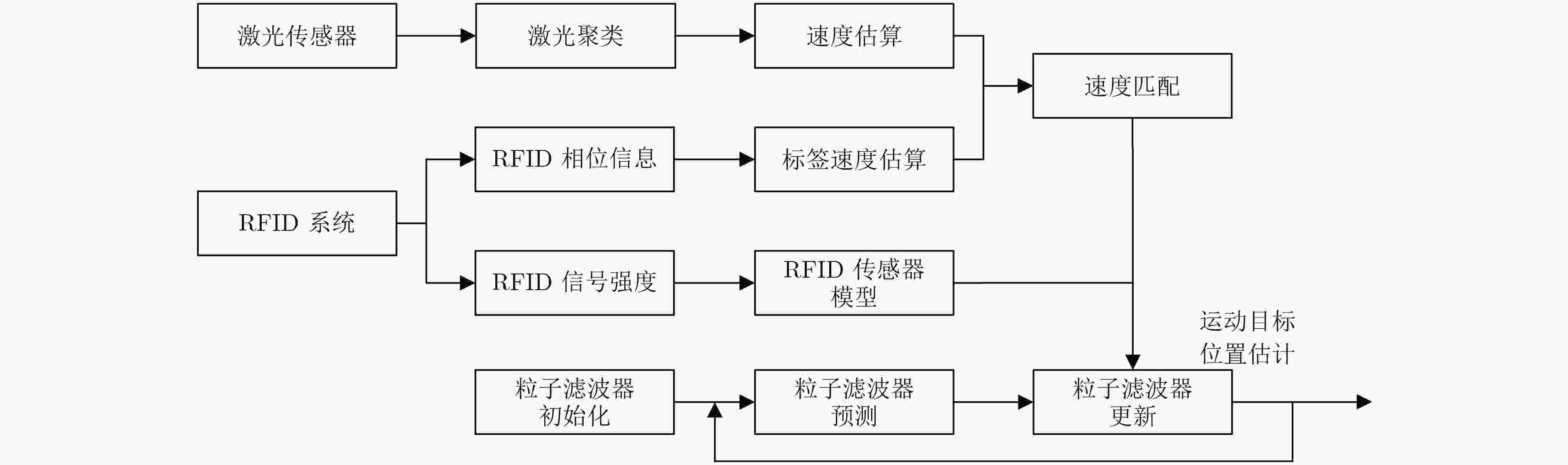
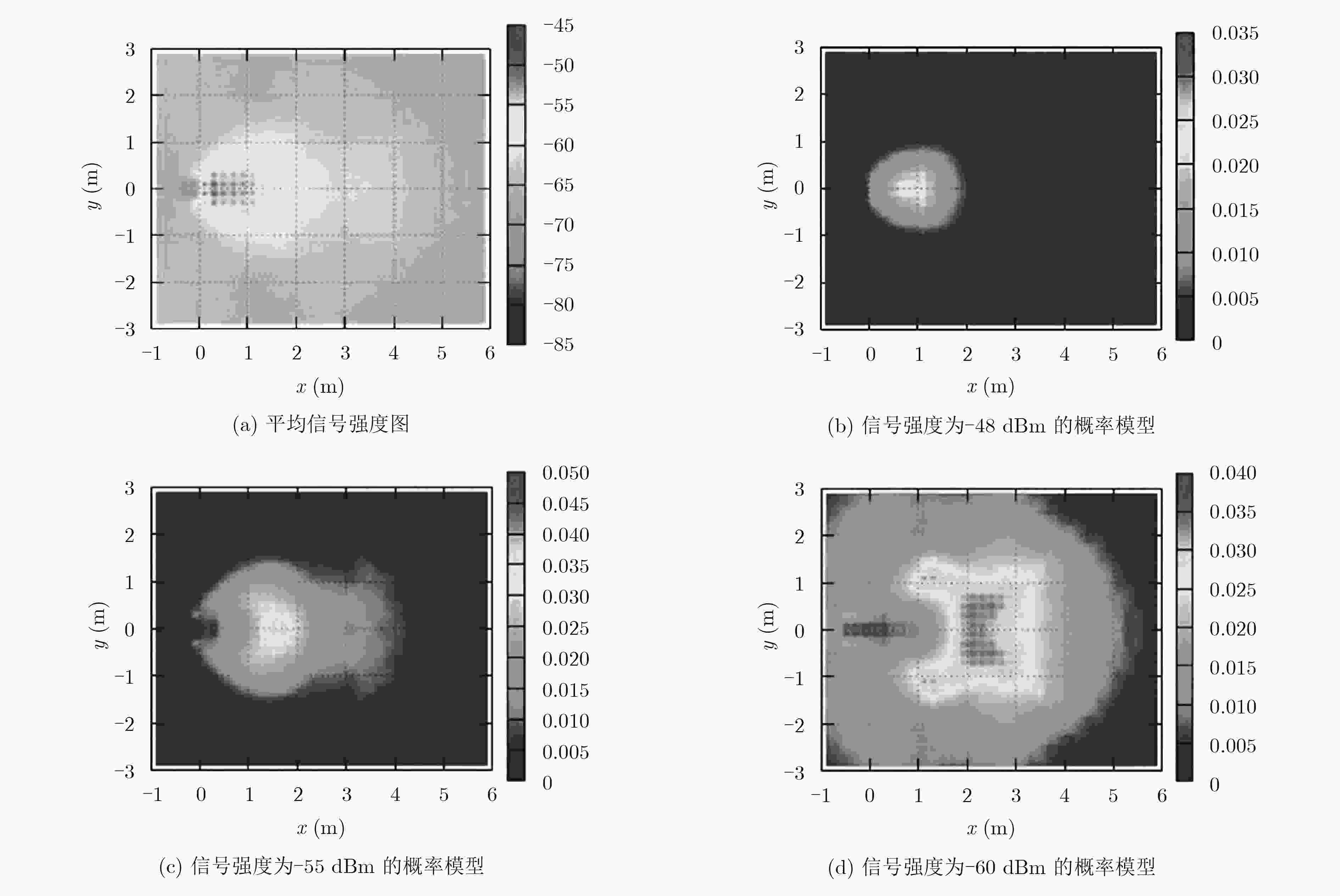
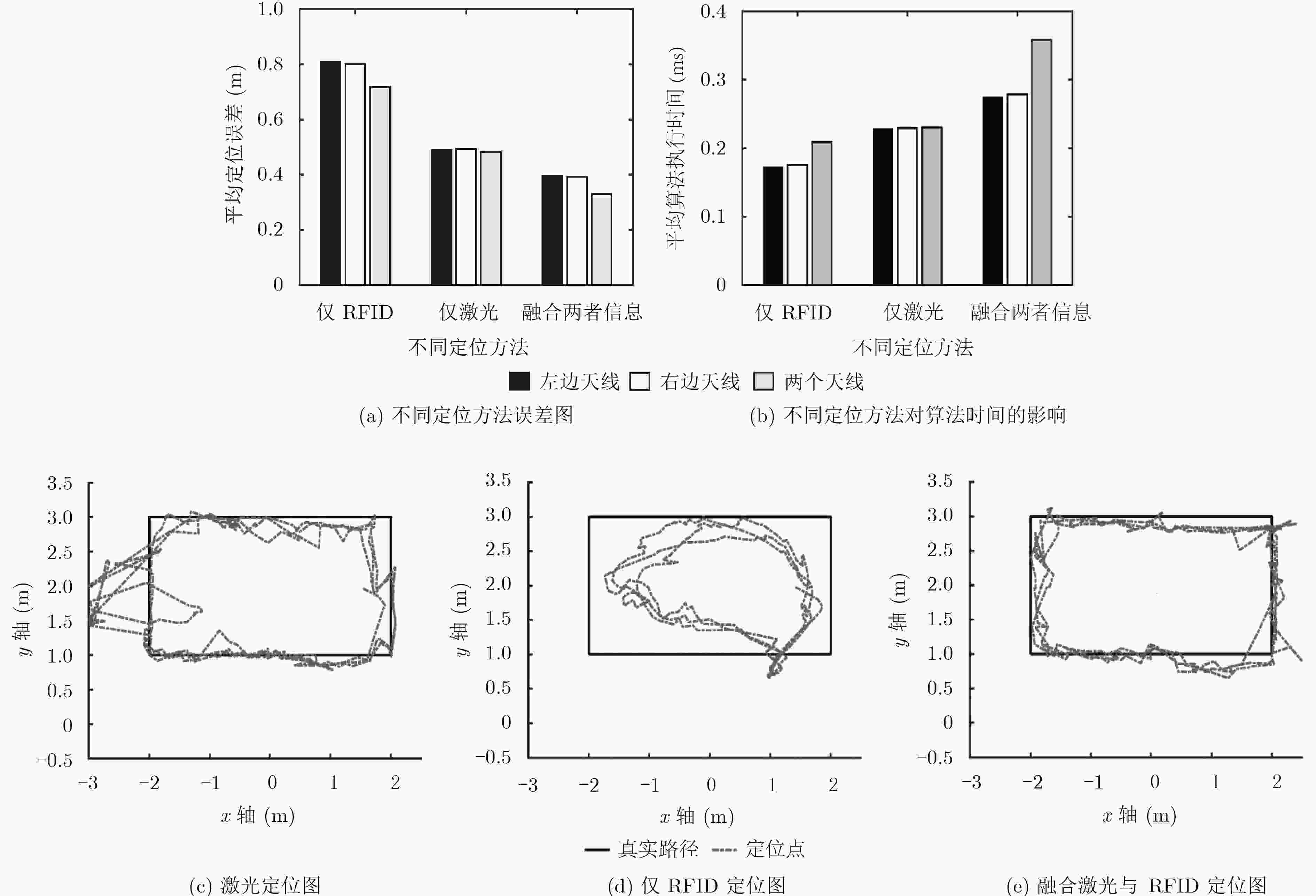
摘要: 低成本、可靠的动态目标定位方法成为目前研究的热点。传统的激光定位或视觉定位方法需要解决识别奇异性和环境遮挡等问题，射频识别(RFID)通过无线射频信号对特定目标进行识别，因此被广泛用于动态目标的定位。该文提出一种融合激光信息与RFID信息对动态目标快速定位的方法。该方法利用粒子滤波器融合RFID信号强度、相位信息和激光数据。首先使用预先训练的信号强度模型将信号强度融入粒子滤波器；然后利用激光聚类后的数据估算运动目标的速度，与RFID相位差估算出的运动目标速度进行匹配；最后利用匹配成功的激光数据对粒子进一步约束。在SCITOS服务机器人上验证了算法的可行性，结果表明，与激光和信号强度的定位方法相比，该方法的定位精度得到了明显提高。
- RSSI信号强度模型 /
- 射频识别相位 /
- 激光聚类 /
- 速度匹配 /
- 粒子滤波
Abstract: Recent researches show great interests in localizing dynamic objects through cost-effective technologies. Laser or visual-based approaches have to solve the singularity and occlusion problem from the environment. Radio Frequency IDentification (RFID) is used as a preferred technology to address these issues, due to the unique identification and the communication without line of sight. In this paper, an innovative method is proposed to localize precisely a dynamic object equipped with an RFID tag by fusing laser information RFID information. A particle filter is used to fuse RFID signal strength, phase information, and laser ranging data. Particularly, a pre-trained signal strength-based model is used to incorporate the signal strength information. Then, the laser ranging data is divided into different clusters and the velocities of these clusters are compared with the RFID phase velocity. Matching results of both velocities are used to confine the locations of the particles during the update stage of the particle filtering. The proposed approach is verified by several experiments on a SCITOS service robot and results show that the proposed approach provides better localization accuracy when compared with laser-based approach and the signal strength-based approach.
- RSSI signal strength model /
- Radio Frequency IDentification (RFID) phase /
- Laser clustering /
- Velocity matching /
- Particle filtering

HTML全文

图 1 定位系统整体框图

下载: 全尺寸图片幻灯片

图 2 激光聚类流程图

下载: 全尺寸图片幻灯片

图 3 RFID传感器特性

下载: 全尺寸图片幻灯片

图 4 实验环境图

下载: 全尺寸图片幻灯片

图 5 不同定位方法对定位误差与算法时间的影响图

下载: 全尺寸图片幻灯片

图 6 不同 ${\lambda _1}$ 和 $\sigma$ 定位误差图与定位图

下载: 全尺寸图片幻灯片

表 2 不同N与K对实验误差的影响 (m)

N	K
N	1	5	8	12	100
20	0.399	0.379	0.365	0.365	0.367
50	0.363	0.342	0.336	0.336	0.338
100	0.349	0.337	0.322	0.324	0.323
500	0.342	0.335	0.320	0.325	0.326

下载: 导出CSV

表 1 不同粒子数N对算法执行时间和定位精度的影响

粒子个数(N)	算法执行时间(ms)	平均定位误差(m)
20	0.145	0.365
50	0.284	0.336
100	0.352	0.322
500	0.856	0.320

下载: 导出CSV

表 3 不同d_g与d_s对定位精度的影响(m)

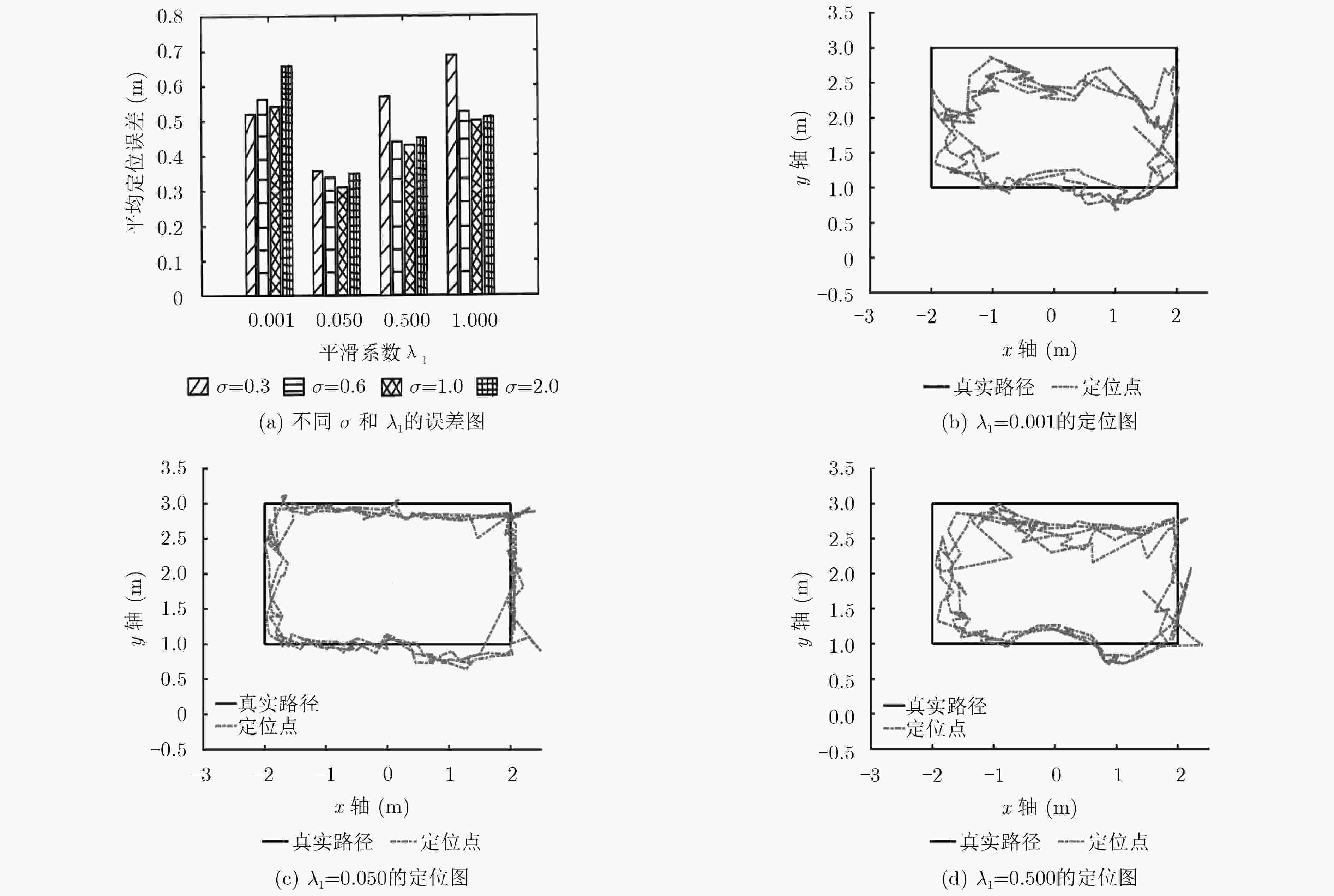
${d_g}$	${d_s}$
${d_g}$	0.05	0.20	1.00	2.00
0.05	0.580	0.598	0.634	0.363
0.20	0.364	0.320	0.371	0.431
1.00	0.578	0.556	0.582	0.622
2.00	0.732	0.695	0.714	0.744

下载: 导出CSV

表 4 不同d_p与R_max对定位精度的影响(m)

${R_{\max }}$	${d_p}$
${R_{\max }}$	0.05	0.10	0.20	0.50
0.20	0.613	0.601	0.648	0.884
0.60	0.323	0.320	0.361	0.661
1.00	0.369	0.366	0.422	0.702
2.00	0.409	0.402	0.444	0.744

下载: 导出CSV

参考文献(18)

WANT R. An introduction to RFID technology[J]. IEEE Pervasive Computing, 2006, 5(1): 25–33 doi: 10.1109/MPRV.2006.2

YANG Zhixin, ZHANG Pengbo, and CHEN Lei. RFID-enabled indoor positioning method for a real-time manufacturing execution system using OS-ELM[J]. Neurocomputing, 2016, 174(PA): 121–133.

PRINSLOO J and MALEKIAN R. Accurate vehicle location system using RFID, an Internet of Things approach[J]. Sensors, 2016, 16(6): 1–24 doi: 10.3390/s16060825

HAHNEL D, BURGARD W, FOX D, et al. Mapping and localization with RFID technology[C]. IEEE International Conference on Robotics and Automation, Brisbane, Australia, 2004: 1015–1020.

VORST P and ZELL A. Semi-autonomous learning of an RFID sensor model for mobile robot self-localization[C]. European Robotics Symposium, Prague, Czech Republic, 2008: 273–282.

JOHO D, PlLAGEMANN C, and BURGARD W. Modeling RFID signal strength and tag detection for localization and mapping[C]. IEEE International Conference on Robotics and Automation, Kobe, Japan, 2009: 3160–3165.

LIONEL M N, LIU Y H, YIU C L, et al. LANDMARC: Indoor location sensing using active RFID[J]. ACM Wireless Networks, 2004, 10(6): 701–710 doi: 10.1023/B:WINE.0000044029.06344

YANG Lei, GUO Yi, LIU Tianci, et al. Perceiving the slightest tag motion beyond localization[J]. IEEE Transactions on Mobile Computing, 2015, 14(11): 2363–2375 doi: 10.1109/TMC.2015.2393859

YANG Lei, CHEN Yekui, LI Xiangyang, et al. Tagoram: Real-time tracking of mobile RFID tags to high precision using COTS devices[C]. Mobile Computing and Networking, New York, USA, 2014: 237–248.

LIU Ran, HUSKIC G, and ZELL A. Dynamic objects tracking with a mobile robot using passive UHF RFID tags[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, USA, 2014: 4247–4252.

LIU Ran, HUSKIC G, and ZELL A. On tracking dynamic objects with long range passive UHF RFID using a mobile robot[J]. International Journal of Distributed Sensor Networks, 2015, 2015(P1): 1–12 doi: 10.1155/2015/781380

LIU Ran, YUEN C, DO T N, et al. Indoor positioning using similarity-based sequence and dead reckoning without training[C]. IEEE International Workshop on Signal Processing Advances in Wireless Communications, Sapporo, Japan, 2017: 1–5.

李军怀, 贾金朋, 王怀军, 等. 基于信号强度差的RFID室内定位[J]. 计算机科学, 2015, 42(11): 154–157 doi: 10.11896/j.issn.1002-137X.2015.11.032

LI Junhuai, JIA Jinpeng, WANG Huaijun, et al. Indoor positioning of RFID based on signal strength difference[J]. Computer Science, 2015, 42(11): 154–157 doi: 10.11896/j.issn.1002-137X.2015.11.032

黄保虎, 刘冉, 张华, 等. 基于不同重采样算法的RFID指纹定位[J]. 计算机应用, 2013, 33(2): 595–599 doi: 10.3724/SP.J.1087.2013.00595

HUANG Baohu, LIU Ran, ZHANG Hua, et al. RFID fingerprinting based on different resampling algorithms[J].Computer Application, 2013, 33(2): 595–599 doi: 10.3724/SP.J.1087.2013.00595

李珣, 刘丽, 洪良, 等. 移动机器人室内无源RFID定位方法及实现[J]. 计算机工程与应用, 2017, 53(16): 230–236 doi: 10.3778/j.issn.1002-8331.1608-0434

LI Xun, LIU Li, HONG Liang, et al. Indoor passive RFID location method for mobile robot and its implementation[J]. Computer Engineering and Application, 2017, 53(16): 230–236 doi: 10.3778/j.issn.1002-8331.1608-0434

黄如林, 梁华为, 陈佳佳, 等. 基于激光雷达的无人驾驶汽车动态障碍物检测、跟踪与识别方法[J]. 机器人, 2016, 38(4): 437–443 doi: 10.13973/j.cnki.robot.2016.0437

HUANG Rulin, LIANG Huawei, CHEN Jiajia, et al. Method of tracking and recognition of laser radar unmanned vehicle dynamic obstacle detection[J]. Robot, 2016, 38(4): 437–443 doi: 10.13973/j.cnki.robot.2016.0437

李昀泽. 基于激光雷达的室内机器人SLAM研究[D]. [硕士论文], 华南理工大学, 2016.

LI Yunze. Research on indoor robot SLAM based on laser radar[D]. [Master dissereation], South China University of Technology, 2016.

PRZYBYLA M. Detection and tracking of 2D geometric obstacles from LRF data[C]. IEEE International Workshop on Robot Motion and Control, Bukowy Dworek, Poland, 2017: 135–141.

施引文献