Calculation of Electromagnetic Propagation Characteristics over Rough Sea Surface Based on Double-layer Model
-
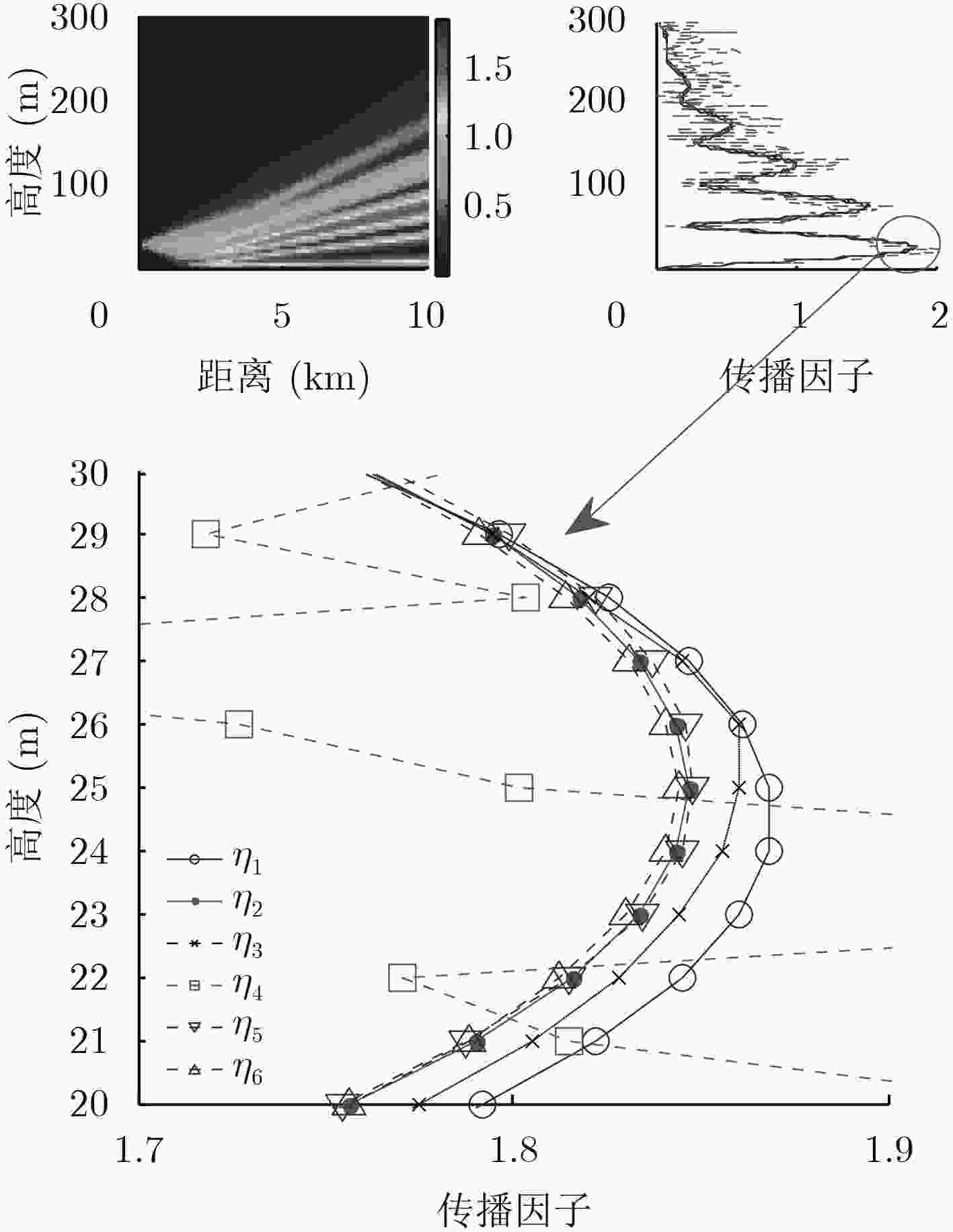
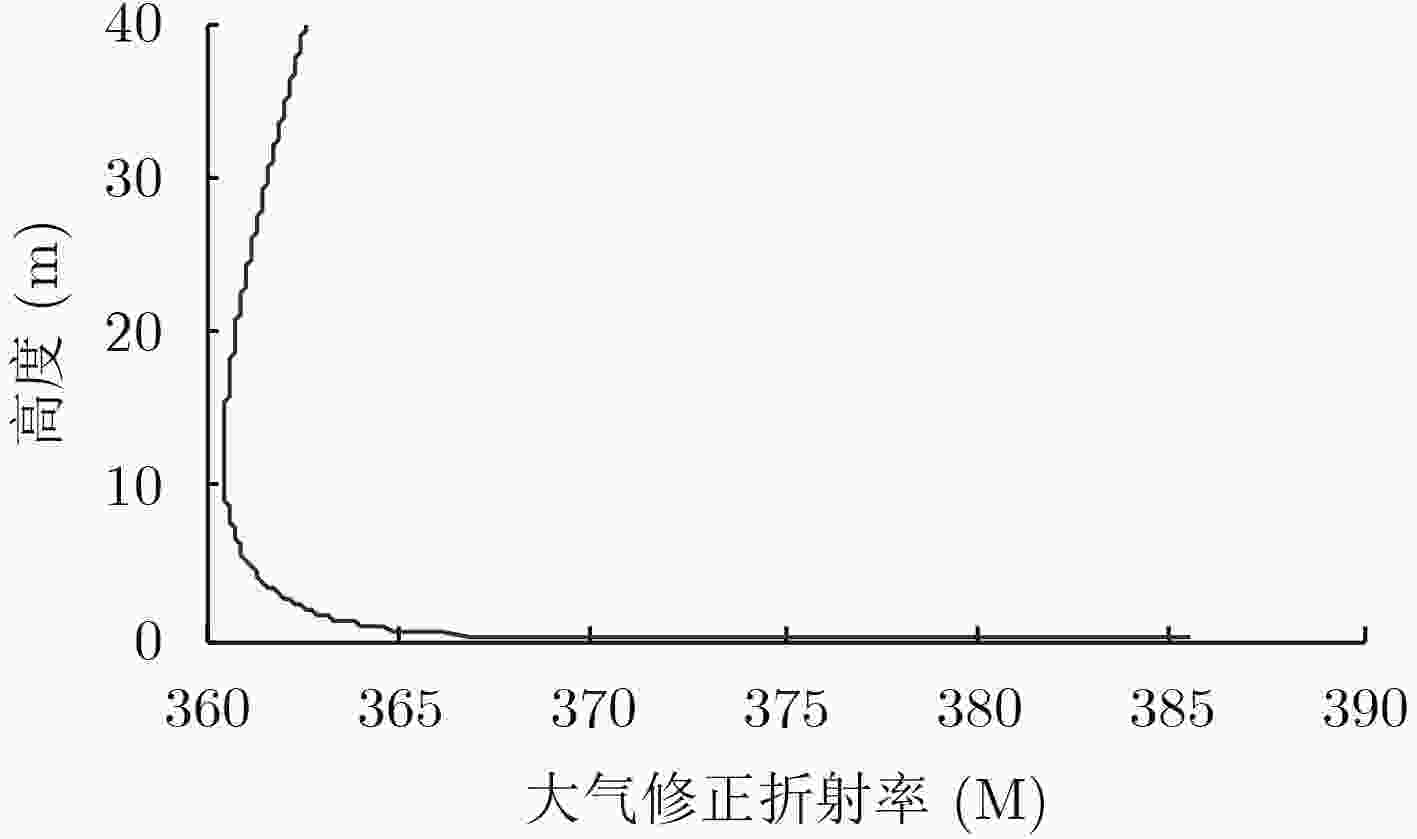
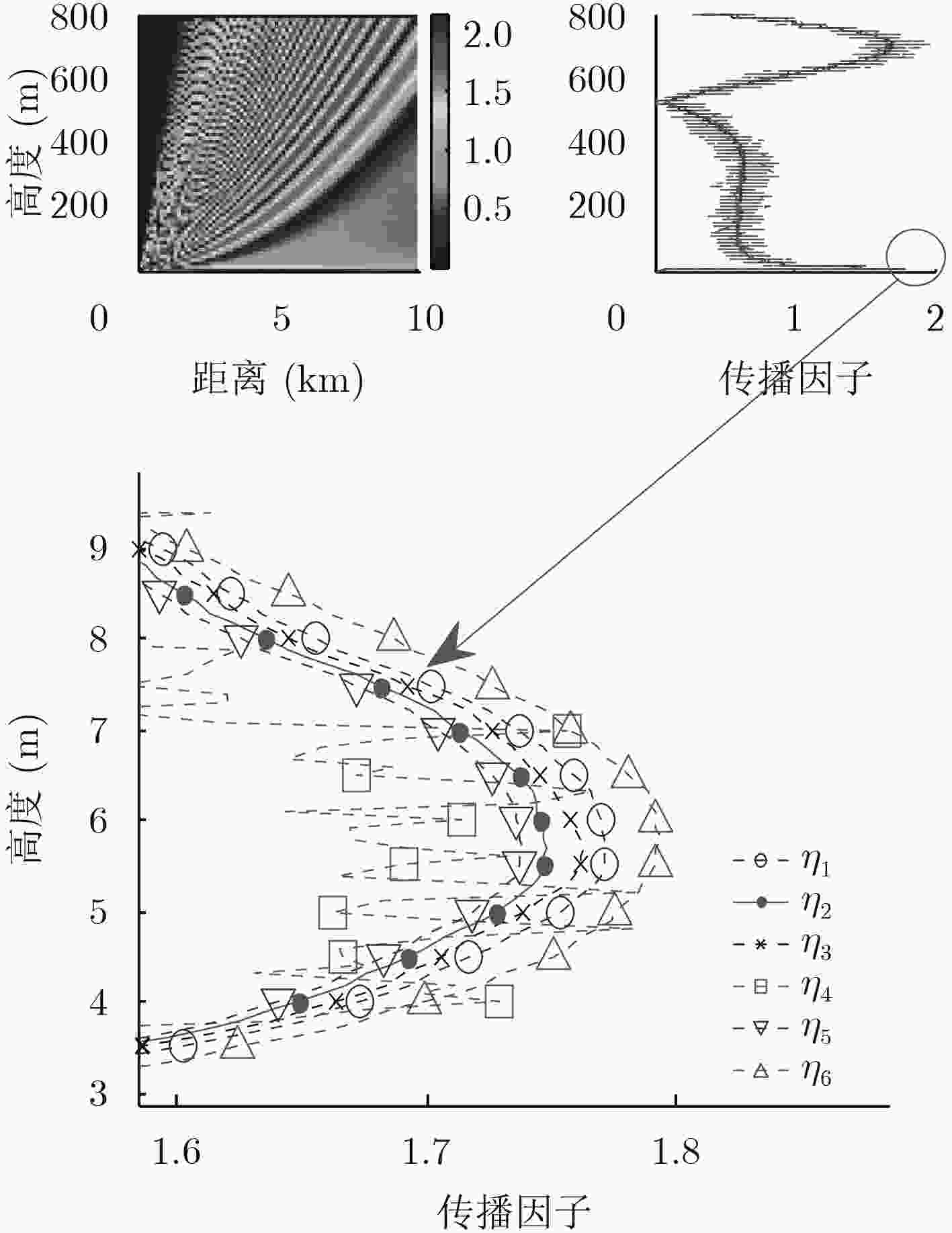
摘要: 针对分段线性地形变换模型运算量较大的问题,该文提出基于双层网格的计算方法,实现了海上大尺度区域复杂电磁环境下电磁波传播特性快速精准的求解。在对宽角抛物方程模型和分段线性地形变换模型的分步傅里叶积分算法研究的基础上,将电磁场计算空间分为上下两层,通过降低计算高度和优化步长的方法,在保证计算精度的同时显著提高了运算效率。通过仿真,在光滑海面和粗糙海面两种条件下对双层网格模型的计算结果与原有模型进行比较,结果表明,所提方法计算误差较小,在粗糙海面条件下运算时间缩短到原模型的1/10。Abstract: A double-layer model is proposed to reduce the calculation amounts of the Linear Ship Map (LSM) model. The proposed model can be used for rapid and accurate calculation of the electromagnetic propagation characteristics in the complicated atmospheric environment over the sea. In the proposed model, the calculation regions are divided into the upper-layer and the lower-layer. The upper-layer is calculated by the Wide angle Parabolic Equation (WPE) model and the lower-layer is calculated by the LSM model. Through reducing the calculation height and optimizing the step length, the proposed model can be exact and rapid. By simulation, the proposed model is compared with LSM model in the smooth and the rough sea surface conditions. The results show that the proposed model can decrease the calculation time by 1/10 in the rough sea surface condition.
-
表 1 网格的参数及运算结果
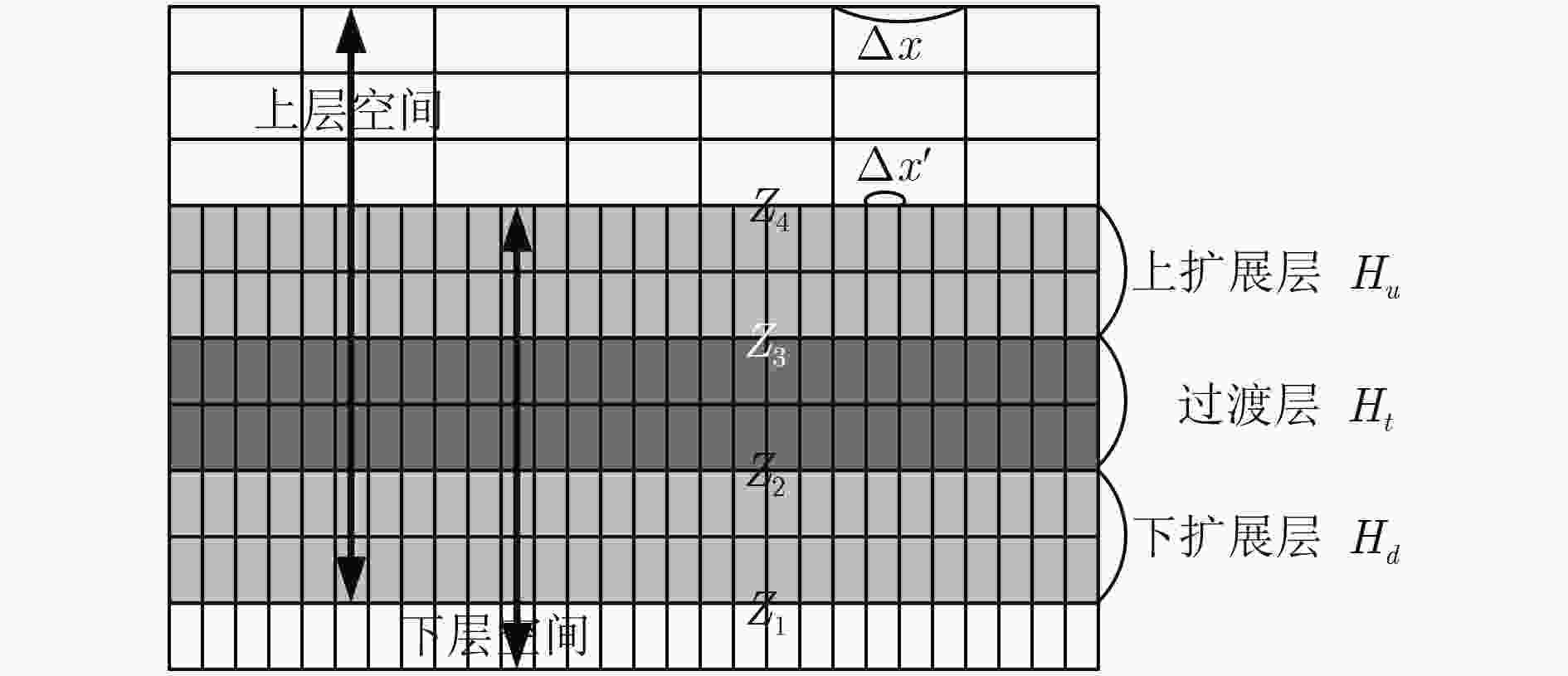
网格条件 小步长(普通网格步长)(m) 大步长(m) ${Z_4}$(m) ${H_t}$(m) 误差 运算时间(s) 1 1 — — — — 4.628 2 1 200 64 10 0.0148 1.200 3 1 200 128 10 0.0080 1.575 4 1 200 64 0 0.1120 1.199 5 1 200 64 20 0.0137 1.199 6 1 50 64 10 0.0138 1.298 表 2 网格的参数及运算结果
网格条件 小步长(普通网格步长)(m) 大步长(m) ${Z_4}$(m) ${H_t}$(m) 误差 运算时间(min) 1 1 — — — — 4.002 2 1 200 51.2 10 0.0140 0.404 3 1 200 102.4 10 0.0118 0.594 4 1 200 51.2 0 0.0958 0.403 5 1 200 51.2 20 0.0103 0.404 6 1 50 51.2 10 0.0203 0.470 -
ZHANG Qi, YANG Kunde, and SHI Yang. Spatial and temporal variability of the evaporation duct in the Gulf of Aden[J]. Tellus, 2016, 68(1): 1–14 doi: 10.3402/tellusa.v68.29792 SIRKOVA I and MIKHAVLEV M. Parabolic wave equation method applied to the tropospheric ducting propagation problem: A survey[J]. Electromagnetics, 2006, 26(2): 155–173 doi: 10.1080/02726340500486484 ZHAO Xiaofeng, HUANG Sixun, and WANG Dongxiao. Using particle filter to track horizontal variations of atmospheric duct structure from radar sea clutter[J]. Atmospheric Measurement Techniques, 2012, 5(11): 2859–2866 doi: 10.5194/amtd-5-6059-2012 刘爱国, 察豪, 李忠猛. 岸基微波超视距雷达探测预报方法[J]. 华中科技大学学报(自然科学版), 2014, 42(7): 96–100 doi: 10.13245/j.hust.140719LIU Aiguo, CHA Hao, and LI Zhongmeng. Prediction method of coastal microwave OTH radar detection range[J]. Journal Huazhong University of Science&Technology(Natural Science Edition) , 2014, 42(7): 96–100 doi: 10.13245/j.hust.140719 李磊, 吴振森, 林乐科, 等. 海上对流层微波超视距传播与海洋大气环境特性相关性研究[J]. 电子与信息学报, 2016, 38(1): 209–215 doi: 10.11999/JEIT150210LI Lei, WU Zhensen, Lin leke, et al. Study on the relativities of the tropospheric microwave trans-horizon propagation above ocean surface and the marine atmospheric environment characteristics[J]. Journal of Electronics&Information Technology, 2016, 38(1): 209–215 doi: 10.11999/JEIT150210 崔萌达, 察豪, 田斌. 雷达威力预报技术中海表温度测量及修正方法[J]. 哈尔滨工业大学学报, 2017, 49(5): 116–121 doi: 10.11918/j.issn.0367-6234.201611018CUI Mengda, CHA Hao, and TIAN Bin. Measurement and modification method of sea surface temperature for radar detection range prediction[J]. Journal of Harbin Institute of Technology, 2017, 49(5): 116–121 doi: 10.11918/j.issn.0367-6234.201611018 ZHANG Pei, BAI Lu, WU Zhensen, et al. Applying the parabolic equation to tropospheric groundwave propagation: A review of recent achievements and significant milestones[J]. IEEE Antennas&Propagation Magazine, 2016, 58(3): 31–44 doi: 10.1109/MAP.2016.2541620 APAYDIN G and SEVGI L. MatLab-based FEM-parabolic equation tool for path loss calculations along multi-mixed-terrain paths[J]. IEEE Antennas and; Propagation Magazine, 2014, 56(3): 221–236 doi: 10.1109/MAP.2014.6867720 FREUND D E, WOODS N E, KU H C, et al. Forward Radar propagation over a rough sea surface: A numerical assessment of the Miller-brown approximation using a horizontally polarized 3-GHz line source[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(4): 1292–1304 doi: 10.1109/TAP.2006.872669 DONOHUE D J and KUTTLER J R. Propagation modeling over terrain using the parabolic wave equation[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(2): 260–277 doi: 10.1109/8.833076 WANG Dandan, XI Xiaoli, PU Yurong, et al. Parabolic equation method for Loran-C ASF prediction over irregular terrain[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15(5): 734–737 doi: 10.1109/LAWP.2015.2471079 BARRIOS A E. Considerations in the development of the advanced propagation model (APM) for U.S. Navy applications[C]. IEEE Radar Conference, Adelaide, Australia, 2003: 77–82. 张青洪, 廖成, 盛楠, 等. 抛物方程方法的亚网格模型及其应用研究[J]. 电子与信息学报, 2014, 36(8): 2005–2009 doi: 10.3724/SP.J.1146.2013.01428ZHANG Qinghong, LIAO Cheng, SHENG Nan, et al. Study on subgridding model of the parabolic equation and its application[J]. Journal of Electronics&Information Technology, 2014, 36(8): 2005–2009 doi: 10.3724/SP.J.1146.2013.01428 魏乔菲, 尹成友, 范启蒙. 存在障碍物时电波传播抛物线方程分析及其验证[J]. 物理学报, 2017, 66(12): 152–159 doi: 10.7498/aps.66.124102WEI Qiaofei, YIN Chengyou, and FAN Qimeng. Research and verification for parabolic equation method of radio wave propagation in obstacle environment[J]. Acta Physica Sinica, 2017, 66(12): 152–159 doi: 10.7498/aps.66.124102 盛楠. 基于抛物方程的复杂气象环境电磁建模及仿真研究[D]. [博士论文], 西南交通大学, 2015.SHENG Nan. Modeling and simulation of complex methorolgical environments based on parabolic equation[D]. [Ph.D. dissertation], Southwest Jiaotong University, 2015. ELFOUHAILY T, CHAPRON B, KATSAROS K, et al. A unified directional spectrum for long and short wind-driven waves[J]. Journal of Geophysical Research, 1997, 102(7): 781–796 doi: 10.1029/97JC00467 -





 下载:
下载:


 下载:
下载:
