1.   引言

雷达目标的高分辨距离像(High Range Resolution Profile, HRRP)表示目标散射中心在雷达-目标方向上的投影，包含了丰富的目标信息。具有易获取、易存储的特点，满足处理时计算量小、实时性强的要求，是目标识别的重要数据来源。研究人员可以基于HRRP提取可分特征进行目标识别。在这一阶段，基于HRRP的目标识别主要集中在分类算法的改进与融合以及依赖研究人员技巧与经验的特征提取，常见的特征有以结构轮廓、强散射点等为代表的时域特征^[1]，也有功率谱、极化矩阵等频域^[2]和极化域^[3]特征等。

随着计算机技术和深度学习理论的发展，深度学习已经成为各领域的研究热点，在合成孔径雷达图像^[4,5]和光学、遥感图像^[6-9]等的目标检测识别方面都得到了广泛应用。雷达基于HRRP的目标识别亦可通过深度学习算法实现^[10-13]。卷积神经网络(Convolutional Neural Network, CNN)是一种重要的深度学习模型，可以自动提取HRRP的有效可分特征，克服不同舰船之间结构相似性和船上建筑对电磁波散射时的高度敏感带来的幅度、平移和姿态角敏感性等问题，相对于传统的分类识别算法而言，识别效果更好。

设计一种良好的神经网络结构是提高分类性能的高效且具有挑战性的方法之一。在数据集样本数量充足的前提下，通过增加神经网络的深度和宽度可以提高模型的学习能力，AlexNet^[14]和VGG^[15]两种结构均证明模型识别准确率在一定范围内与网络深度成正相关。但是随着网络深度增加，卷积神经网络在训练时的反向传播过程中可能会出现梯度爆炸、消失以及网络识别率饱和的问题。即网络无法学习到新的有效特征，识别准确率随着网络深度增加而下降。针对这一问题，文献[16]提出残差结构，通过跳跃连接保持浅层特征的完整性，避免网络性能随着深度增加而降低。但是残差结构网络仍需要增加网络深度来提高识别效果。本文通过改进残差结构提出一种高效可扩展的神经网络，在减少网络参数的情况下达到深层网络的识别效果。同时通过模块化结构的设计，使模型可以进行高效的扩展以适应不同难度的分类任务。仿真结果表明，与传统算法相比该模型可以得到更高的识别准确率。

2.   1维卷积神经网络

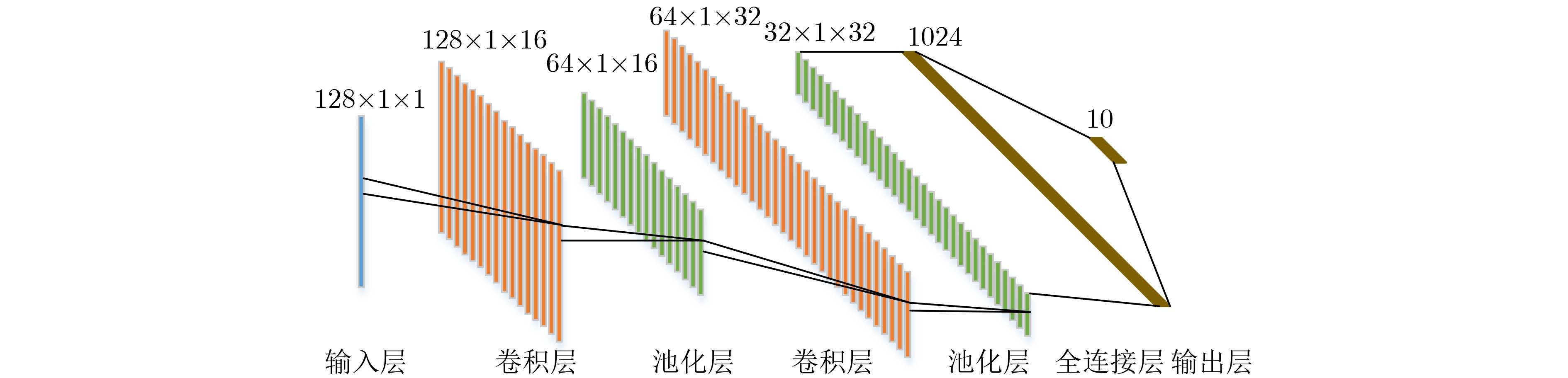
卷积神经网络是一种包含卷积计算的前馈神经网络，由于具有平移不变性的特点，可以避免对HRRP数据对齐等复杂的预处理，具有较好的鲁棒性。本文所用模型以卷积神经网络为基础，这里首先对其基本结构进行介绍，主要包括：输入层、卷积层、池化层、全连接层、输出层5个部分。针对HRRP的CNN结构如图1所示。图1展示了CNN对一个长度为128的HRRP 数据进行10种类别目标的分类过程。

图 1  针对HRRP的CNN结构示意图

下载: 全尺寸图片 幻灯片

输入层是神经网络的起点，需要对数据进行简单的预处理，使数据具有相同的维度并且满足相同的分布特征。可分两步进行：(1)归一化。对数据幅度进行归一化处理。对第$n$个HRRP数据${{{x}}_n}$而言，幅度归一化后的数据表示为${{{x}}'_n} = {{{x}}_n}/\max (\left| {{{{x}}_n}} \right|)$。其中$\max (\left| {{{{x}}_n}} \right|)$为该HRRP数据中所有元素的绝对值最大值。(2)零均值。对归一化后的HRRP数据各元素分别减去该HRRP数据的均值。

卷积层的主要作用是对输入数据的特征进行提取，一般卷积层的内部可以包含多个卷积核。图1中两个卷积层分别包含16个和32个卷积核，每个卷积核元素包含权重系数和偏差值。卷积核对输入数据进行卷积计算并加入偏差值，利用激活函数进行激活，其输出即为提取的特征。计算过程可以由式(1)表示。

式中，${{x}}$表示特征项；${{M}}$表示输入特征项的集合；${{k}}$为卷积核；${{b}}$为偏差值；$l$是网络结构的层序号；$i$是卷积核序号；$j$是特征项通道序号；$f$是激活函数。卷积层的参数包括卷积核大小、步长、填充类别和激活函数，常用的激活函数有Sigmoid函数、Relu函数等，不同的参数赋予卷积层不同的特性。

池化层的作用是通过下采样来实现对卷积层提取特征的选择和降维。常用的池化层有最大池化、均值池化以及混合池化等。全连接层通常放在神经网络的后部，主要作用是将上一层得到的特征按顺序排列得到1维向量。其输出通过输出层分类器得到整个CNN的结果。常用的分类器有Softmax和支持向量机等。在目标识别问题中，CNN的输出可以是目标的类别、大小和中心坐标等。针对监督学习的CNN学习过程一般通过反向传播进行参数的迭代更新，通过使损失函数计算的误差值最小来获得稳定的识别结果。

3.   模型的分析与设计

3.1   卷积模块的设计

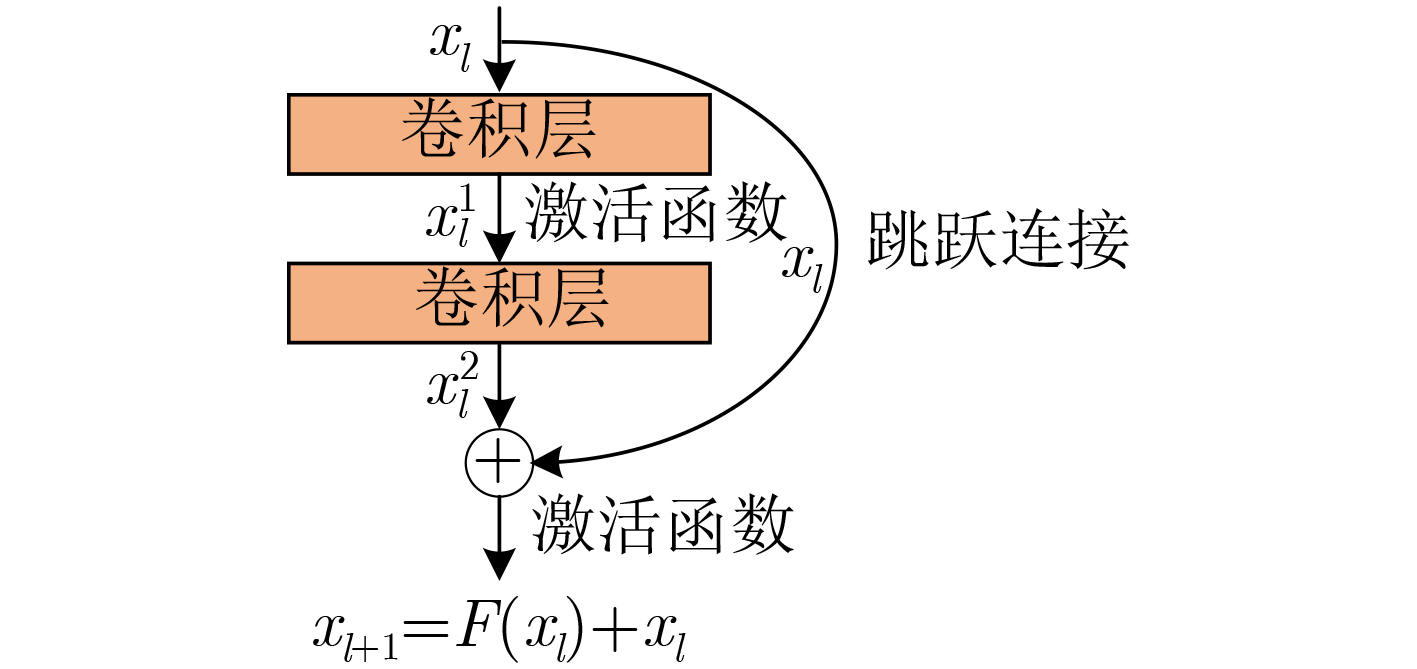
神经网络的深度至关重要，深层卷积神经网络可以提取并融合不同层次的特征用于端到端的目标识别。但是网络层数变深会带来识别准确率饱和的问题，克服这一问题一般引入残差结构，其结构如图2所示。

图 2  残差结构

下载: 全尺寸图片 幻灯片

残差结构中的残差块由卷积层组成，图中卷积层数量为2。残差结构的输出为输入特征与最后一个卷积层的输出相加，由式(2)表示

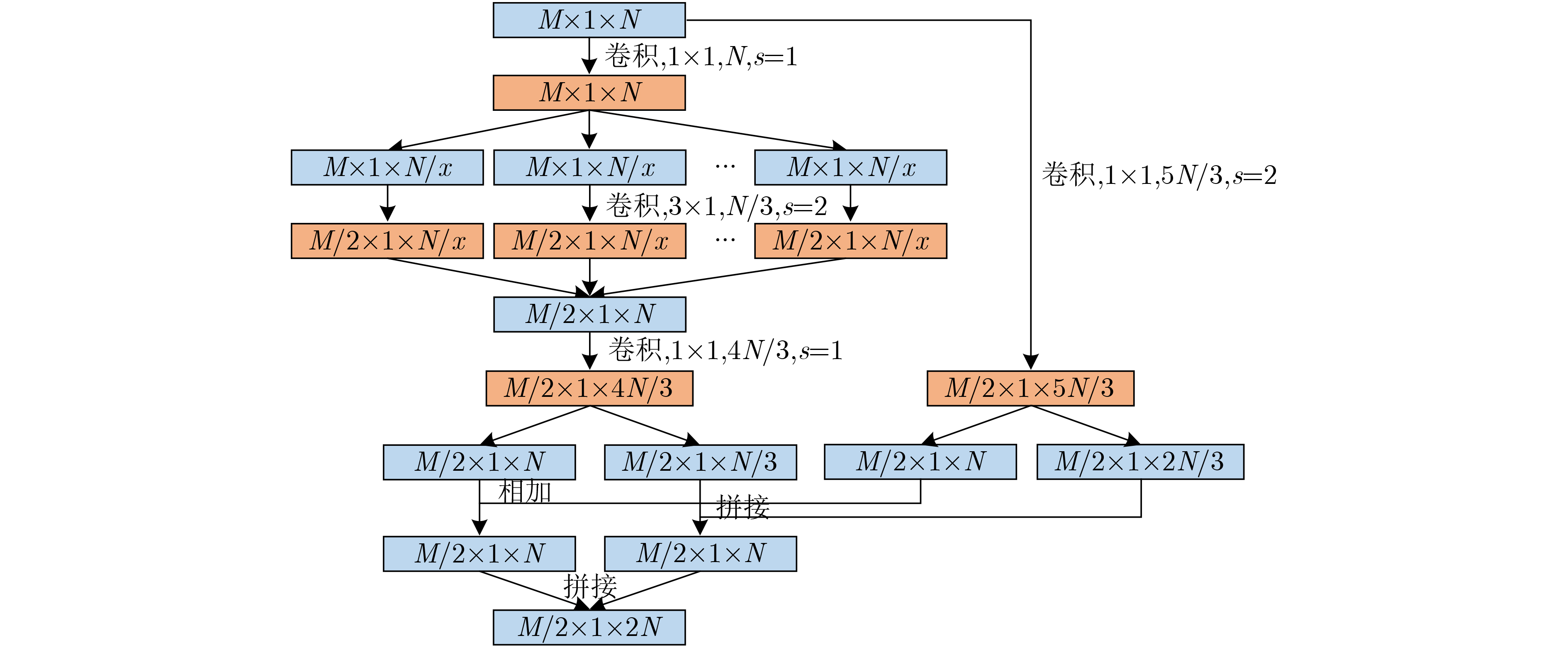
式中，${x_l}$, ${x_{l + 1}}$分别表示第$l$层残差结构的输入和输出特征；$F\left( {{x_l}} \right)$表示残差块的映射。

研究表明，通过拟合映射$F\left( {{{{x}}_l}} \right)$来代替所需映射$F\left( {{x_l}} \right) + {x_l}$可以有效缓解深层网络识别准确率饱和的问题^[16]。因为极端情况下，若网络已经提取出分类所需最佳特征，则残差结构只需进行跳跃连接的恒等映射即可保证最高的识别准确率。而对神经网络而言，将残差块置零比利用多层神经网络拟合恒等映射更加高效。

本文在残差结构基础上改进得到的卷积模块结构如图3所示，图中M×1×N表示输入特征为M×1的1维数据，特征层数为N, s为卷积核的移动步长。卷积模块设置为高度模块化的网络结构，可扩展性强。上层网络提取的特征作为本层网络的输入，输入将通过2个支路。在左侧支路中，首先利用1×1的卷积核对不同层之间的特征进行融合，融合后的特征在层数上被等分为多个支路(图中用x表示)，每个支路3层特征，各支路分别利用3×1的卷积核进行特征提取，步长为2，特征层数不变，维度减半。然后将多个支路特征进行拼接，可以根据分类任务的复杂度确定x的大小。这种结构与Inception^[17]结构类似，但是Inception中各支路卷积核的大小和数量都是逐级定制的。这里统一选择3×1的小尺度卷积核来降低结构设计难度，同时保证识别效果。拼接后的特征再次使用1×1的卷积核进行特征融合并增加特征层数，特征按层分为两个部分，为后续两条支路特征融合做准备。右侧支路直接使用1×1的卷积核对输入进行特征融合并增加特征层数，同时将特征按层数分为两个部分，与左侧支路对应特征进行相加和拼接操作，如图3所示。

图 3  卷积模块结构

下载: 全尺寸图片 幻灯片

卷积模块的输出相对输入而言，特征维度减半、层数加倍。右侧支路的效果与残差网络类似，可以使网络模块的每一层都从损失函数和原始输入信号中获取信息，更加有效地传递特征和梯度，提高浅层特征的利用率，解决随着网络不断加深可能产生的梯度消失和识别率饱和的问题。

3.2   损失函数的设计

损失函数用于度量预测值与真实值之间的差异，一般用$L\left( {y\_,{\kern 1pt} {\kern 1pt} {\kern 1pt} y} \right)$表示，其中$y\_$表示预测值，$y$表示真实值。对于多分类的卷积神经网络，通常使用SL(Softmax Loss)作为损失函数。但是从聚类角度看，SL提取的特征会出现类内距离大于类间距离的情况。同时，SL提取的特征在可视化时呈发散状，当目标类别过多时会导致特征重叠，不利于目标分类。

对目标分类时，我们不仅希望特征是可分的，还要求特征之间有较大差异。CL^[18](Center Loss)损失函数可以对每类目标特征构建一个类中心，通过惩罚远离类中心的特征减小类内距离。引入参数$\lambda$将CL与SL融合得到联合损失函数$L$，如式(3)所示

式中，${L_{\rm{s}}}$表示SL; ${L_{\rm{c}}}$表示CL; $\lambda$表示$L$中${L_{\rm{c}}}$所占权重，需合理设置；${{{x}}_i} \in {\mathbb{R}^d}$表示第$i$个特征，$d$表示特征维数；${{{W}}_j} \in {\mathbb{R}^d}$表示权值矩阵${{W}} \in {\mathbb{R}^{d \times n}}$的第$j$列；${{b}} \in {\mathbb{R}^n}$表示偏置项；$m$, $n$分别表示批处理时每批数据的个数和目标的类别个数；${{{c}}_{{y_i}}} \in {\mathbb{R}^d}$表示第${y_i}$个类别的特征中心，${{{c}}_{{y_i}}}$随着每批数据特征的变化而不断更新。

联合损失函数中${L_{\rm{c}}}$相对于${{{x}}_i}$的梯度以及${{{c}}_{{y_i}}}$的更新方程为

式中，当${y_i}$为第$j$类目标时，识别正确，此时$\delta \left( \cdot \right)$等于1，否则$\delta \left( \cdot \right)$等于0。

3.3   模型结构的设计

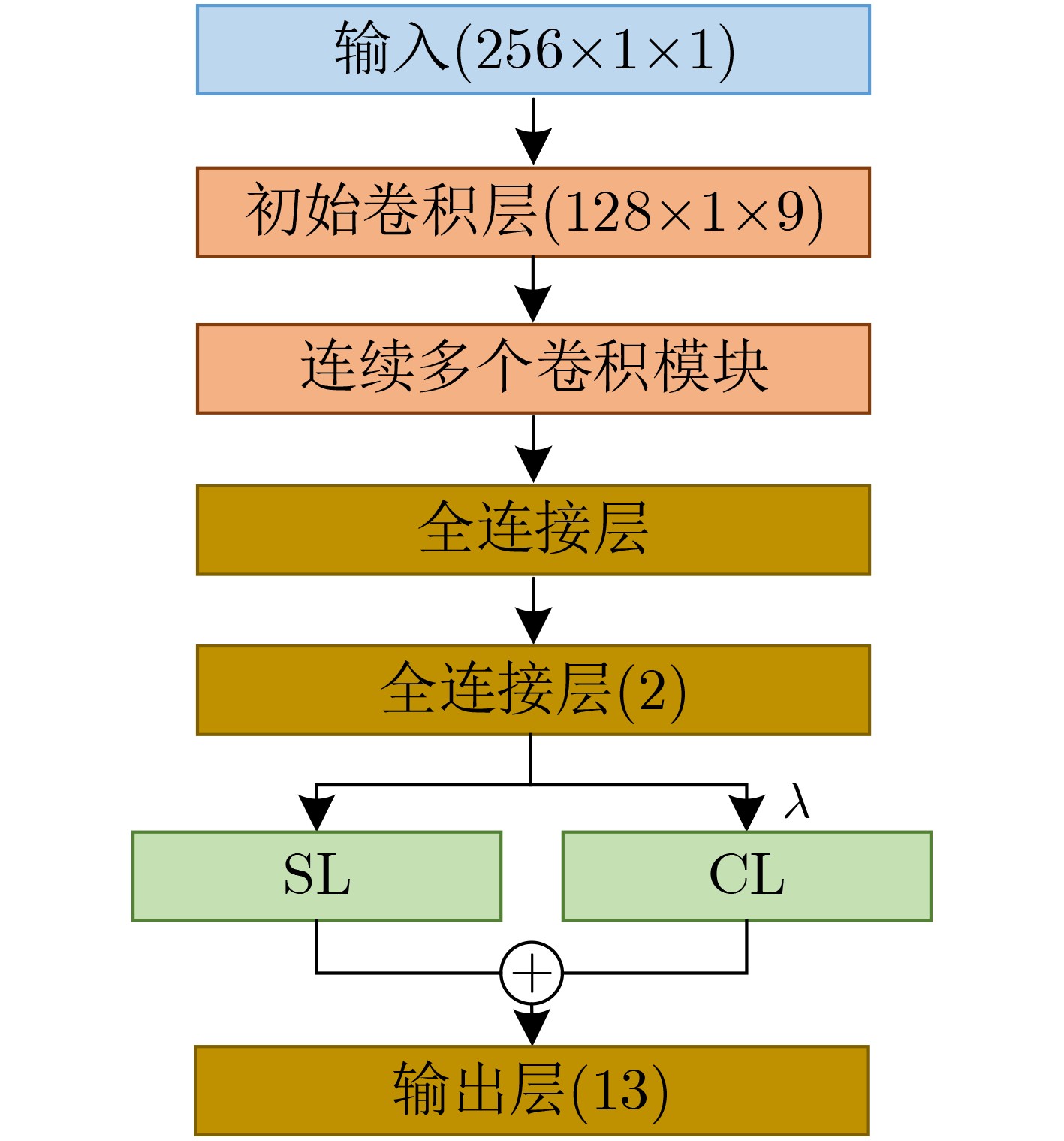
本文模型框图如图4所示，主要包含一个初始卷积层、顺序连接的多个相同拓扑结构卷积模块和最后的两个全连接层。后一个全连接层的维度为2，便于将模型提取的特征可视化，分析特征的聚类效果。

图 4  本文所提模型框图

下载: 全尺寸图片 幻灯片

括号内数字表示HRRP样本通过该层后的数据维度，与图3相同。卷积模块和第一个全连接层的输出数据维度根据卷积模块个数确定。输出层的结果是与目标类别对应的1维数据，图中目标类别为13。模型中初始卷积层选择尺度为7×1的1维卷积核，在网络第1层选用尺度较大的卷积核有利于提取目标HRRP数据中对应的轮廓、纹理等特征。模型中每次卷积操作后都对提取的特征进行批量归一化和Relu激活操作。

4.   实验仿真与分析

4.1   数据集的构建

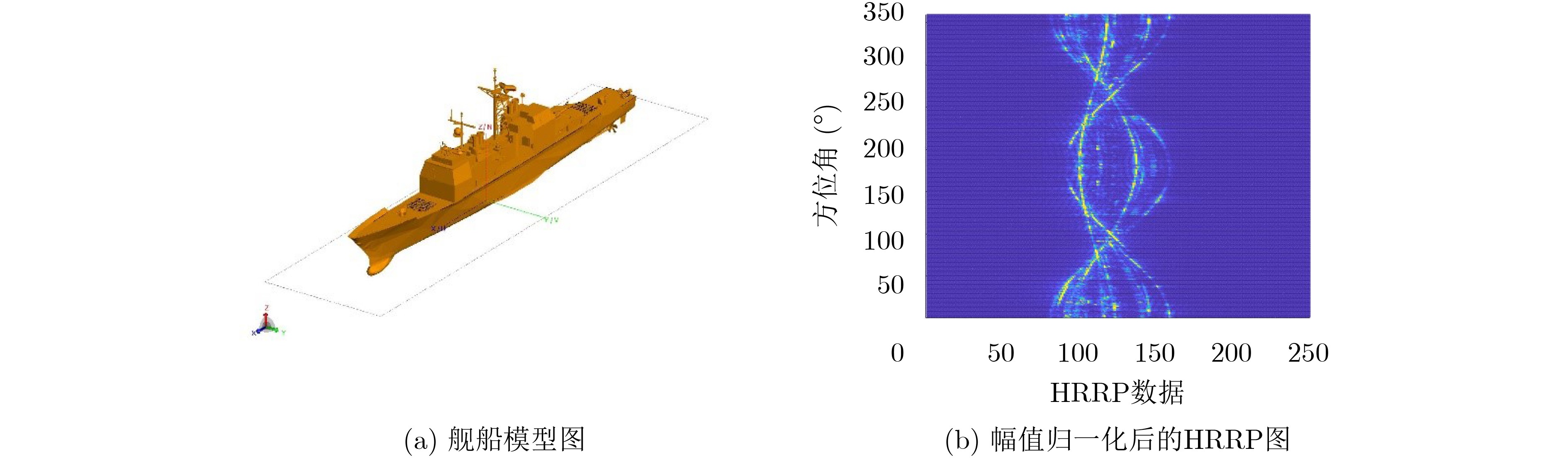
通常对目标回波信号的获取有两个途径：实测法和理论计算法。由于所关注的舰船目标多为非合作目标，通过外场实测得到其HRRP极为困难。本文通过3D Max软件建立了13种舰船模型，利用FEKO软件计算得到HRRP。仿真参数设置如下：雷达中心频率10 GHz，带宽80 MHz，频率采样点数256个。计算方位角范围为0～360°，间隔1°，俯仰角为90°(水平方向)。得到的HRRP具有256个距离单元，每个分辨单元对应长度为1.875 m。其中一艘舰船的模型和幅值归一化后的HRRP图如图5所示。

图 5  某艘舰船模型图及其对应幅值归一化后的HRRP图

下载: 全尺寸图片 幻灯片

图5(b)中横轴表示HRRP长度，纵轴表示方位角。各舰船分别得到360个HRRP数据。为满足神经网络训练时对样本数据量的要求，防止过拟合，需要对数据集进行扩充。过程如下：

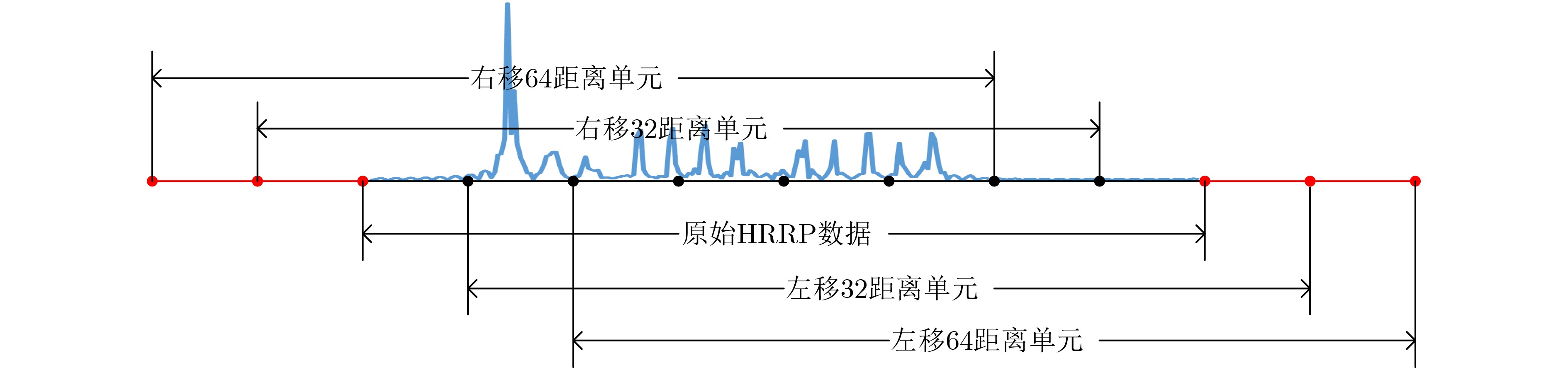
(1) 对HRRP进行平移截取。由图5可以看出，对舰船HRRP计算时，坐标轴与舰船中心重合，使得HRRP有效信息均在中间区域。而雷达对目标实际探测时会出现回波信号不完整或部分缺失的情况，因此数据扩充首先对HRRP平移截取，依次将HRRP向左右各平移32和64个距离单元，移出的数据丢弃，空白部分用0补齐，如图6所示。通过截取HRRP样本中部分重合但不完全相同的部分将样本数量变为5倍。

图 6  HRRP数据平移截取示意图

下载: 全尺寸图片 幻灯片

(2) 对平移得到的HRRP数据添加随机噪声。对数据添加10次高斯白噪声，并使添加噪声后的数据满足一定的信噪比。随机选择每类舰船目标数据的2/3作为训练集，1/3作为测试集，则数据库中训练集样本为156000个，测试集样本为78000个。

4.2   模型识别性能分析

4.2.1   模型复杂度对识别效果的影响

实验运行环境如下，操作系统：Windows10; GPU: NVIDIA GeForce RTX 2080 Ti; CPU: Intel(R) Xeon(R) W-2125 CPU @4.00 GHz；内存：64 GB。随着模型深度和宽度的增加，模型的超参数越来越多，复杂度也越来越高。设计识别准确率高、复杂度低、超参数少、易扩展的模型是本文关注的重点。本文所提模型的超参数限定在卷积模块的个数、模块内部左侧支路的数量和联合损失函数权重3个参数，通过选择不同的参数得到3个不同复杂度的模型。模型A复杂度最低，卷积模块个数为4个，模块内部左侧支路数量为3个；模型B通过将模型A中卷积模块个数增加到5个得到；模型C通过将模型A中左侧支路数量增加到6个得到。篇幅限制这里仅给出模型A各阶段结构和参数明细，如表1所示。参数统计时包括卷积核和批量归一化的参数个数。

表 1  模型A各阶段参数情况

阶段	输出	结构		参数个数
初始卷积层	128×1×9	7×1, 9, s=2		99
		左侧支路	右侧支路
卷积模块1	64×1×18	1×1, 9 3×1, 3, s=2, x=3 1×1, 12	1×1, 15, s=2	585
卷积模块2	32×1×36	1×1, 18 3×1, 6, s=2, x=3 1×1, 24	1×1, 30, s=2	1980
卷积模块3	16×1×72	1×1, 36 3×1, 12, s=2, x=3 1×1, 48	1×1, 60, s=2	7200
卷积模块4	8×1×144	1×1, 72 3×1, 24, s=2, x=3 1×1, 96	1×1, 120, s=2	27360
全连接层1	144	全局平均池化+全局最大值池化		0
全连接层2	2			288
输出层	13	SL+CL		26
	参数总数		37538

下载: 导出CSV 

| 显示表格

分别以信噪比为0, 5, 10和15 dB的数据集对模型进行训练和识别。识别准确率通过计算测试数据集中被正确分类的样本个数占样本总数的百分比得到。识别结果以及识别单个HRRP所需时间如表2所示。

表 2  不同复杂度模型在不同信噪比数据集下的识别准确率(%)

模型名称	识别时间(μs)	信噪比(dB)
		0	5	10	15
模型A	258	60.42	89.41	98.21	99.83
模型B	326	72.95	94.41	99.15	99.89
模型C	323	73.78	93.71	99.07	99.86

下载: 导出CSV 

| 显示表格

由表2中可以看出，信噪比对模型的识别准确率有较大的影响。在信噪比为15 dB时，3个模型均取得了很好的识别效果，结构最简单的模型A识别准确率虽然最低，但也达到了99.83%。随着信噪比的降低，3个模型的识别准确率均不同程度降低。对比模型A，模型B和C的识别准确率降低较小，特别是在信噪比较低时，差别更为明显。说明虽然随着模型深度和宽度的提升，模型复杂度更高，但是模型可以提取出HRRP数据中更深层、更稳定的可分特征用于识别，使得模型对噪声的适应性更强。但同时可以看出，与模型A相比，模型B和C的计算时间随着模型复杂度的增加而增加。

4.2.2   模型与其他识别方法的识别效果对比

本节的对比模型选择常见的神经网络，分别为卷积神经网络^[11](CNN)、栈式卷积自动编码器^[12](Stacked Convolutional Auto Encoder, SCAE)和栈式降噪稀疏自动编码器与K最近邻^[13](Stacked Denoising Sparse Auto Encoder &K-Nearest Neighbor, SDSAE&KNN)。设置对比模型时，保证各模型参数数量相近，分析复杂度相近时不同模型的识别准确率差别。对比模型的结构和参数明细如表3至表5所示，模型中池化层均为最大池化，CNN中卷积层后均进行批量归一化操作。

表 3  CNN模型结构和参数明细

阶段	输出维度	网络结构	参数个数
卷积层1	256×1×8	3×1, 8, s=1	64
池化层1	128×1×8	2×1, s=2	0
卷积层2	128×1×16	3×1, 16, s=1	464
池化层2	64×1×16	2×1, s=2	0
卷积层3	64×1×32	3×1, 32, s=1	1696
池化层3	32×1×32	2×1, s=2	0
卷积层4	32×1×64	3×1, 64, s=1	6464
池化层4	16×1×64	2×1, s=2	0
卷积层5	16×1×64	1×1, 64, s=1	4416
池化层5	8×1×64	2×1, s=2	0
全连接层1	64		32832
全连接层2	2		130
输出层	13	SL	39
参数总数		46105

下载: 导出CSV 

| 显示表格

表 4  SDSAE&KNN模型结构和参数明细

阶段	输出维度	参数个数
隐藏层1	150×1	38550
隐藏层2	100×1	15100
隐藏层3	50×1	5050
隐藏层4	10×1	510
参数总数	59210

下载: 导出CSV 

| 显示表格

表 5  SCAE模型结构和参数明细

阶段	输出维度	网络结构	参数个数
卷积层1	256×1×128	5×1, 128, s=1	768
池化层1	128×1×128	2×1, s=2	0
卷积层2	128×1×64	5×1, 64, s=1	41024
池化层2	64×1×64	2×1, s=2	0
卷积层3	64×1×32	3×1, 32, s=1	6176
池化层3	32×1×32	2×1, s=2	0
卷积层4	32×1×16	3×1, 16, s=1	1552
池化层4	16×1×16	2×1, s=2	0
卷积层5	16×1×8	1×1, 8, s=1	136
池化层5	8×1×8	2×1, s=2	0
输出层	13	SL	845
参数总数		50501

下载: 导出CSV 

| 显示表格

本文使用模型的参数总数代表模型的空间复杂度，可以看出，各模型空间复杂度从小到大依次为：模型A,CNN,SCAE和SDSAE&KNN。同样以信噪比为0,5,10和15 dB的数据集对模型进行训练和识别，对比不同信噪比条件下，模型的识别准确率。识别结果以及识别单个HRRP所需时间如表6所示。

表 6  不同信噪比条件下本节模型与对比模型识别准确率(%)

模型名称	识别时间(μs)	信噪比(dB)
		0	5	10	15
模型A	258	60.42	89.41	98.21	99.83
CNN	69	58.22	86.91	95.51	98.79
SCAE	47	54.78	86.58	94.44	98.78
SDSAE&KNN	68	46.50	83.94	93.44	98.65

下载: 导出CSV 

| 显示表格

从表6可以看出，各模型识别准确率同样随着信噪比增大而增大。与对比模型相比，模型A参数数量最少，模型复杂度更低，在不同信噪比条件下均取得了最高的识别准确率，在不增加复杂度的情况下具有最好的识别效果和更好的噪声鲁棒性。需要注意的是，由于所提模型计算过程更加复杂，需要更多的时间来识别目标。同时对比不同模型可以看出，前3个模型的识别准确率均大于第4个，说明包含卷积结构的模型识别效果更好，使用卷积核有助于对可分特征的提取。

4.2.3   损失函数对模型识别效果的影响

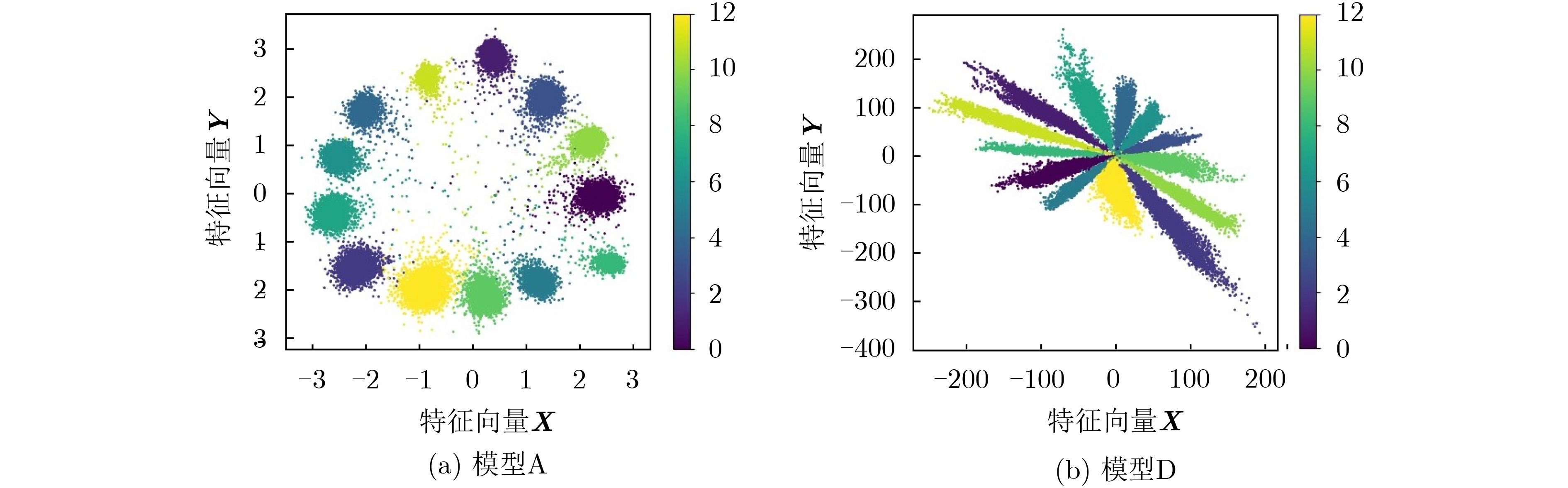
本文选择融合SL和CL的联合损失函数度量模型预测值与实际值的差别进行反向传播，为验证损失函数的有效性，将模型A损失函数简化为SL得到模型D，对比两模型识别效果。在数据集信噪比为15 dB时，全连接层2中的2维特征可视化如图7所示。此时权重$\lambda = 0.2$，特征中心的更新率为0.5。

图 7  信噪比为15 dB时不同模型的特征可视化图

下载: 全尺寸图片 幻灯片

图7中每个数据点表示模型从HRRP数据中提取的2维特征，不同颜色代表不同的目标类别。可以看出，使用不同损失函数时，模型所提取的特征可视化结果存在截然不同的模式。这是因为本文采用余弦距离来衡量特征之间的相似度，即特征点之间的夹角越大，类间距离越大，相似性越低。SL损失函数仅通过增大不同目标类别特征之间的余弦距离来区分目标。而所提联合损失函数则增加了类内距离约束，通过惩罚远离类中心的特征点来减小同一特征的类内距离。因此，在特征可视化时同一类别的特征逐渐向各自类中心聚集，呈现出图7(a)中的模式。模型A的2维特征尺度更小、聚类性更好，仿真结果表明识别准确率比模型D高1.6%。使用联合损失函数有助于减小同一目标的类内距离，一定程度上提高识别准确率，但是相对损失函数而言，合理的网络结构对识别准确率的影响更大。

5.   结束语

本文提出了一种具有高效的微块内部结构和残差网络结构的神经网络模型，用于对舰船目标基于HRRP数据的分类识别。模型具有超参数少、易扩展、识别准确率高的特点，其中卷积模块设置为简单、高度模块化的网络结构，可扩展性强。通过卷积模块左侧支路分支结构模拟网络加深加宽的效果，利用右侧支路的跳跃结构更加有效地传递特征和梯度，提高浅层特征利用率，降低梯度消失和识别率饱和的风险。同时使用联合损失函数约束同一目标的类内距离，进一步提高识别准确率。仿真结果表明，该模型相比于其他常见网络结构，在模型参数更少的情况下，识别效果更好，同时具有更强的噪声鲁棒性。