面向全覆盖路径规划的类Rulkov混沌映射算法设计

刘思聪; 何明; 李春彪; 韩伟; 刘承卓; 夏恒煜

doi:10.11999/JEIT250887

面向全覆盖路径规划的类Rulkov混沌映射算法设计

doi: 10.11999/JEIT250887 cstr: 32379.14.JEIT250887

刘思聪^{1, 2},
何明^1, ,,
李春彪³,
韩伟¹,
刘承卓¹,
夏恒煜¹

1.
陆军工程大学指挥与控制学院南京 210045
2.
江苏经贸职业技术学院物联网与智能工程学院南京 210045
3.
南京信息工程大学人工智能学院南京 210044

基金项目: 国家自然科学基金(62273356)，国家人才项目(2022-JCJQ-ZQ-001)，江苏省重点研发计划(BE2021729)，高层次人才创新工程(KYZYJQJY2101)，国家重点研发计划(2024YFF1401400)

详细信息

作者简介:
刘思聪：男，副教授，研究方向为离散混沌映射、集群控制

何明：男，教授，研究方向为集群控制

李春彪：男，教授，研究方向为混沌映射、非线性动力学系统

韩伟：女，副教授，研究方向为集群控制

刘承卓：男，硕士生，研究方向为集群控制

夏恒煜：男，硕士生，研究方向为集群控制

通讯作者:
何明　heming@aeu.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 93
- HTML全文浏览量: 35
- PDF下载量: 23
- 被引次数: 0
出版历程
- 收稿日期: 2025-09-09
- 修回日期: 2025-11-03
- 录用日期: 2025-11-03
- 网络出版日期: 2025-11-13

Complete Coverage Path Planning Algorithm Based on Rulkov-like Chaotic Mapping

1.
School of Command and Control Engineering, Army Engineering University of PLA, Nanjing 210045, China
2.
School of Artificial intelligence and Engineering, Jiangsu Vocational Institute of Commerce, Nanjing 210045, China
3.
School of Artificial Intelligence, Nanjing University of Information Science and Technology, Nanjing 210044, China

Funds: The National Natural Science Foundation of China (62273356), The National Talent Project of China (2022-JCJQ-ZQ-001), Jiangsu Provincial Primary Research and Development Plan (BE2021729), High-level Talent Innovation Project (KYZYJQJY2101), The National Key Research and Development Program (2024YFF1401400)

摘要

摘要: 该研究提出了一种基于正弦约束的类Rulkov超混沌映射(SRHC)系统，并将其应用于全覆盖路径规划算法(SRHC-CCPP)中，以解决智能机器人在复杂任务场景中的全覆盖路径规划问题。通过引入超混沌序列，该算法显著提升了机器人运动路径的随机性和动态性，避免了传统算法因规律性过强而可能陷入局部循环的问题。同时，结合记忆效应，算法能够动态记录网格访问历史，优先覆盖未访问区域，从而有效减少重复访问，提升覆盖效率。在障碍物处理方面，设计了碰撞检测与法线向量反射机制，使机器人能够灵活应对复杂环境中的障碍物干扰，并通过轻微扰动避免局部振荡。实验结果表明，SRHC-CCPP算法在无障碍和有障碍物条件下均表现出较高的覆盖速度和均匀性，展现了良好的初始值敏感性和鲁棒性。此外，算法的计算复杂度较低，适合大规模应用场景。该研究为智能机器人在灾区救援、火灾扑灭及未知地域勘探等高风险任务中的应用提供了新的技术支持。
- 全覆盖路径规划算法 /
- 超混沌映射 /
- 记忆效应 /
- 障碍物处理 /
- 初始值敏感性
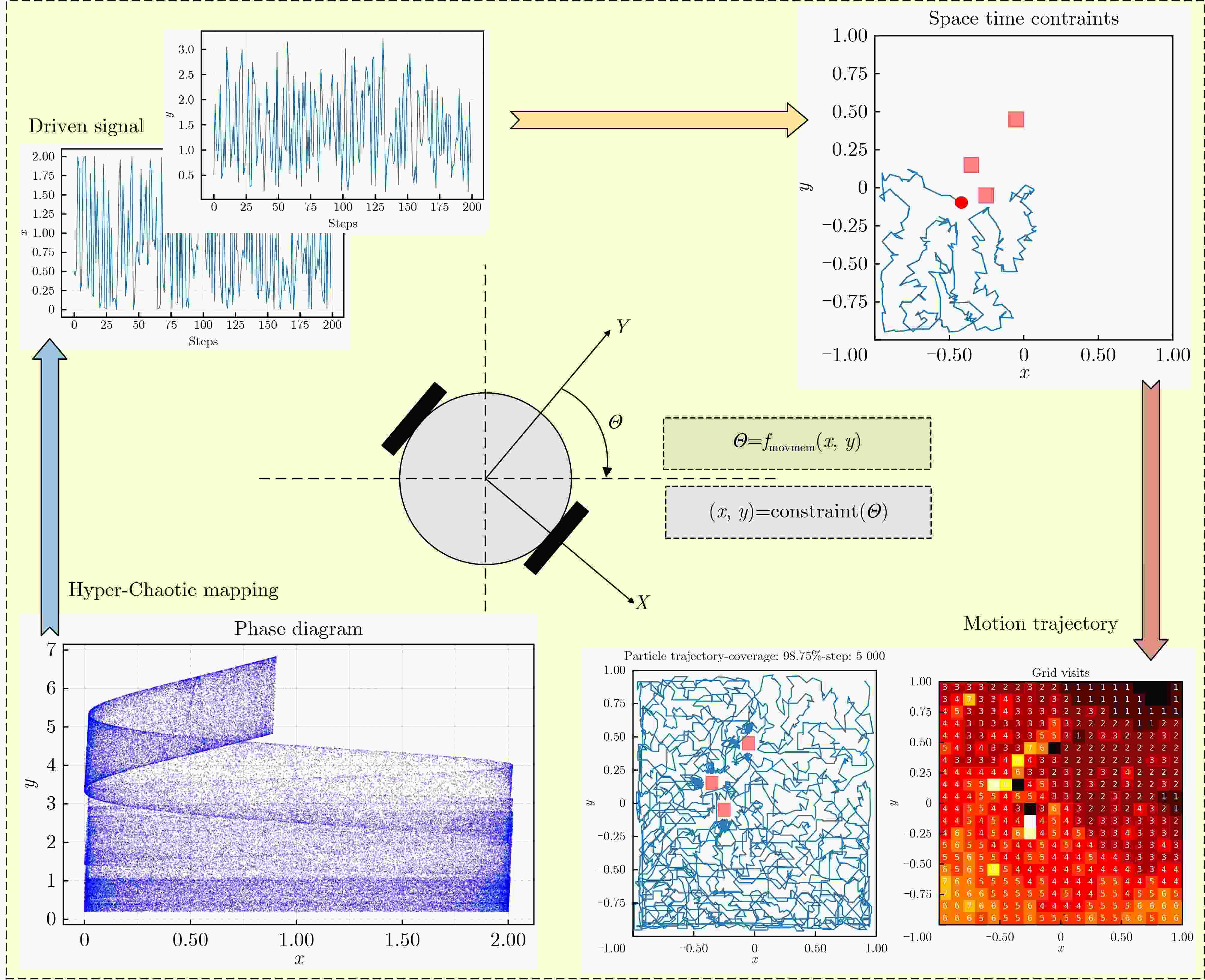
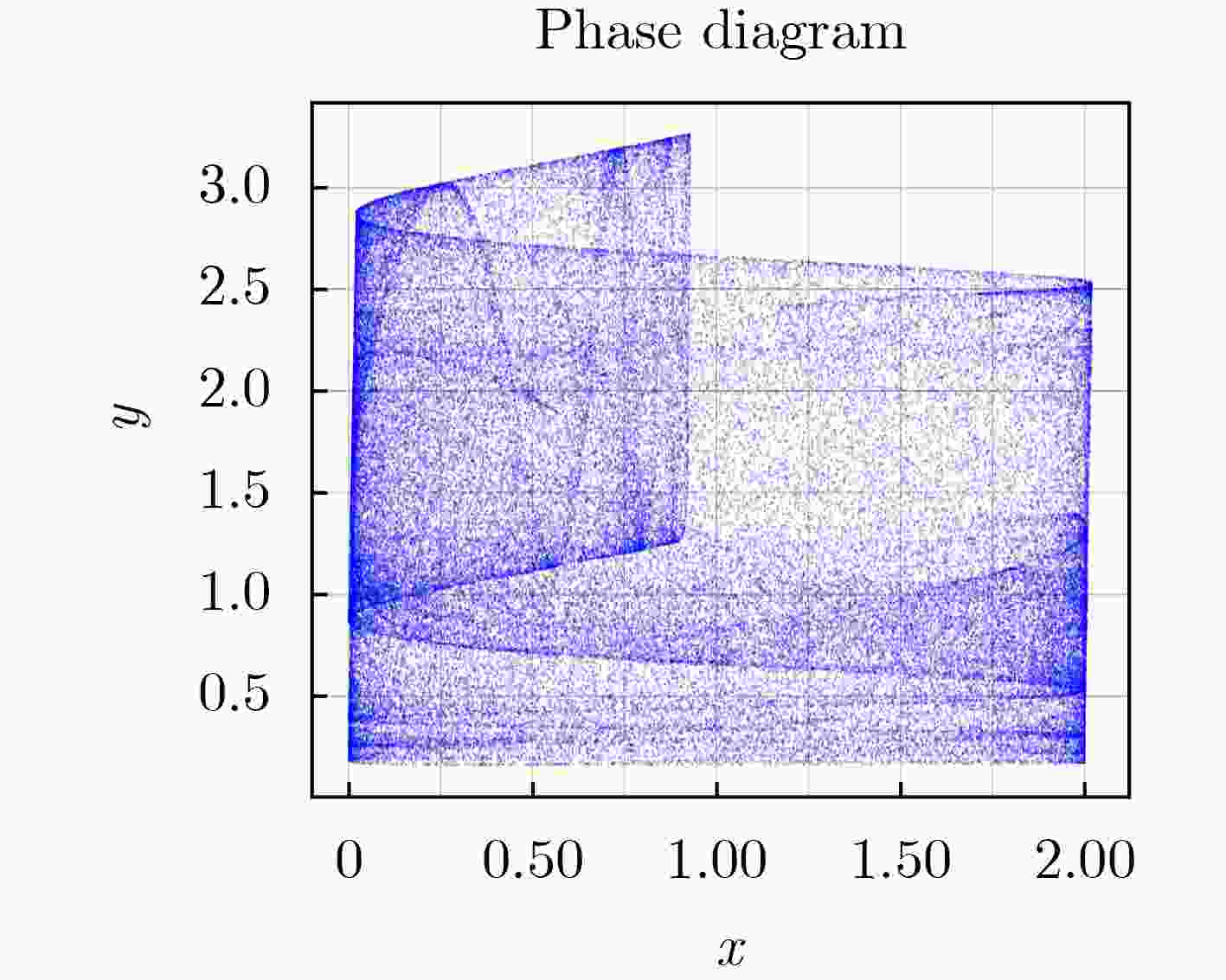
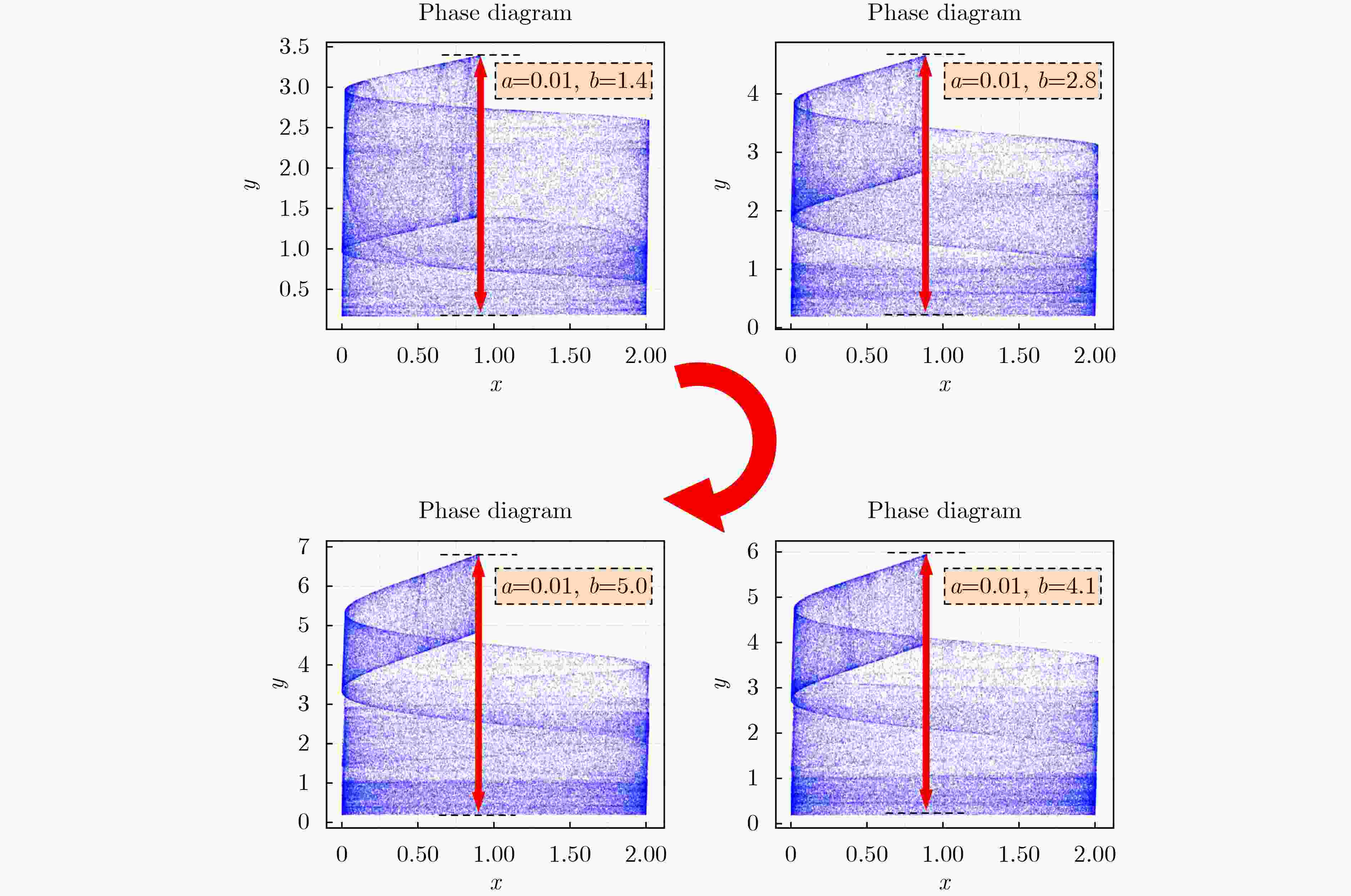
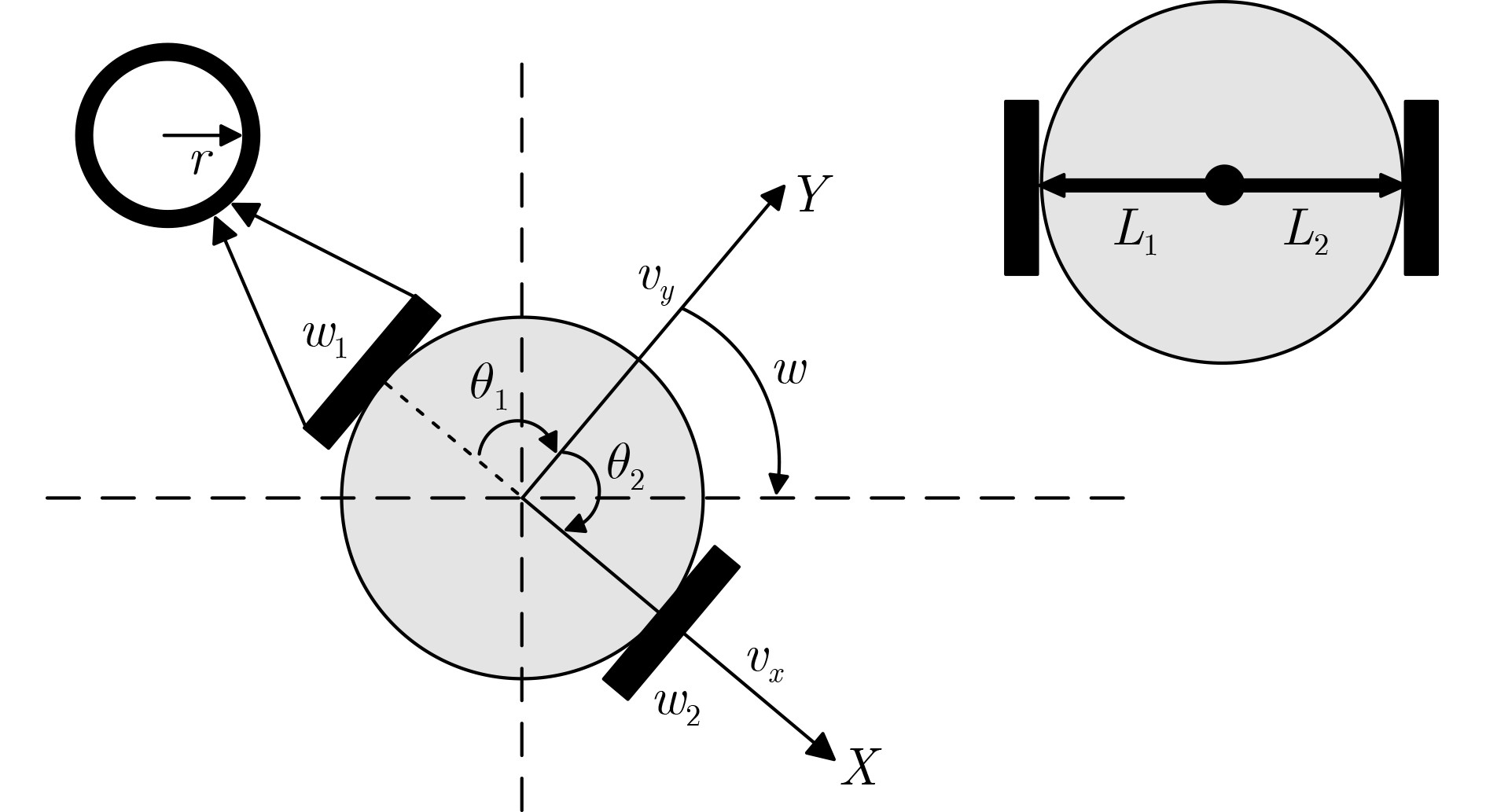
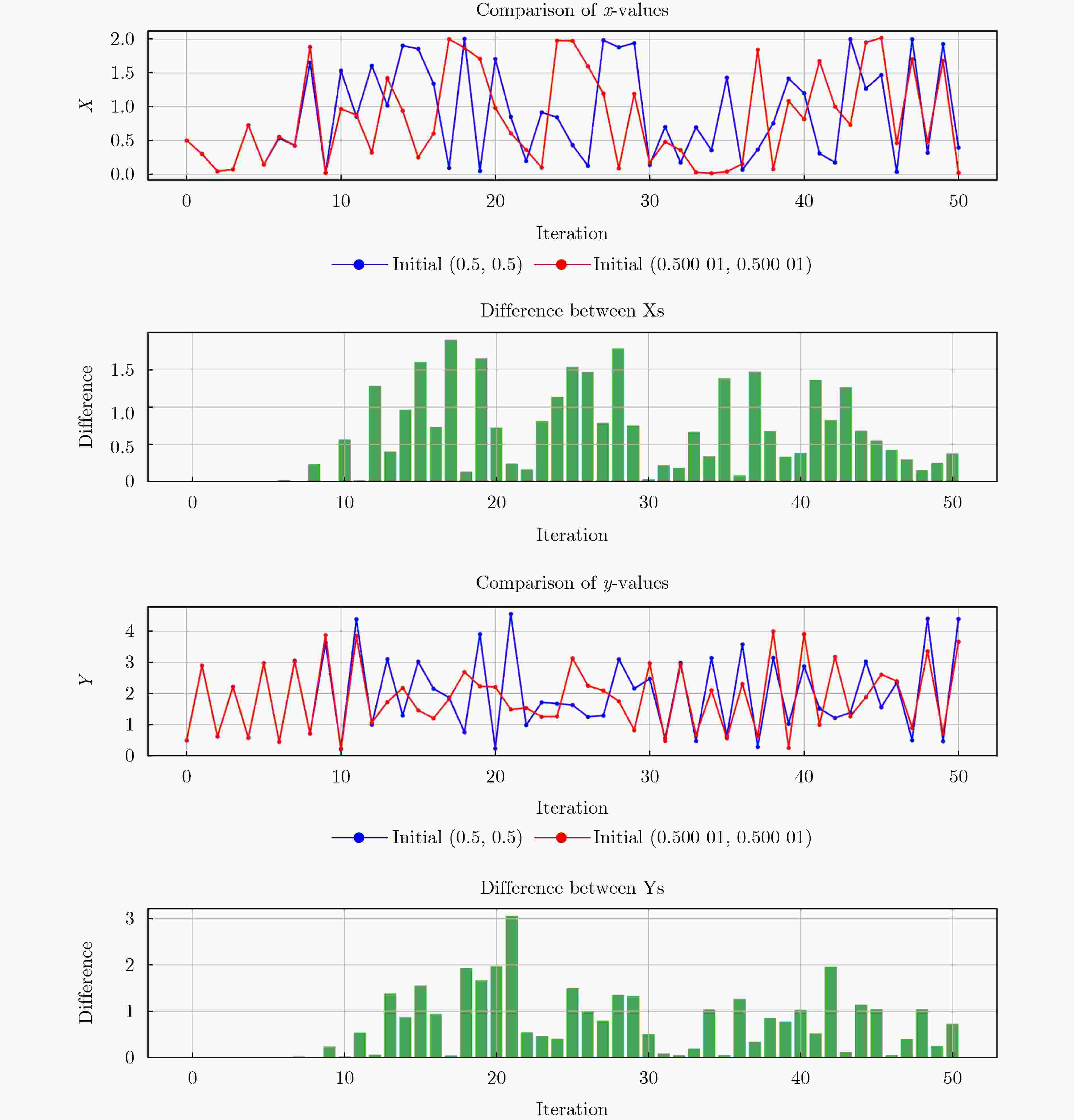
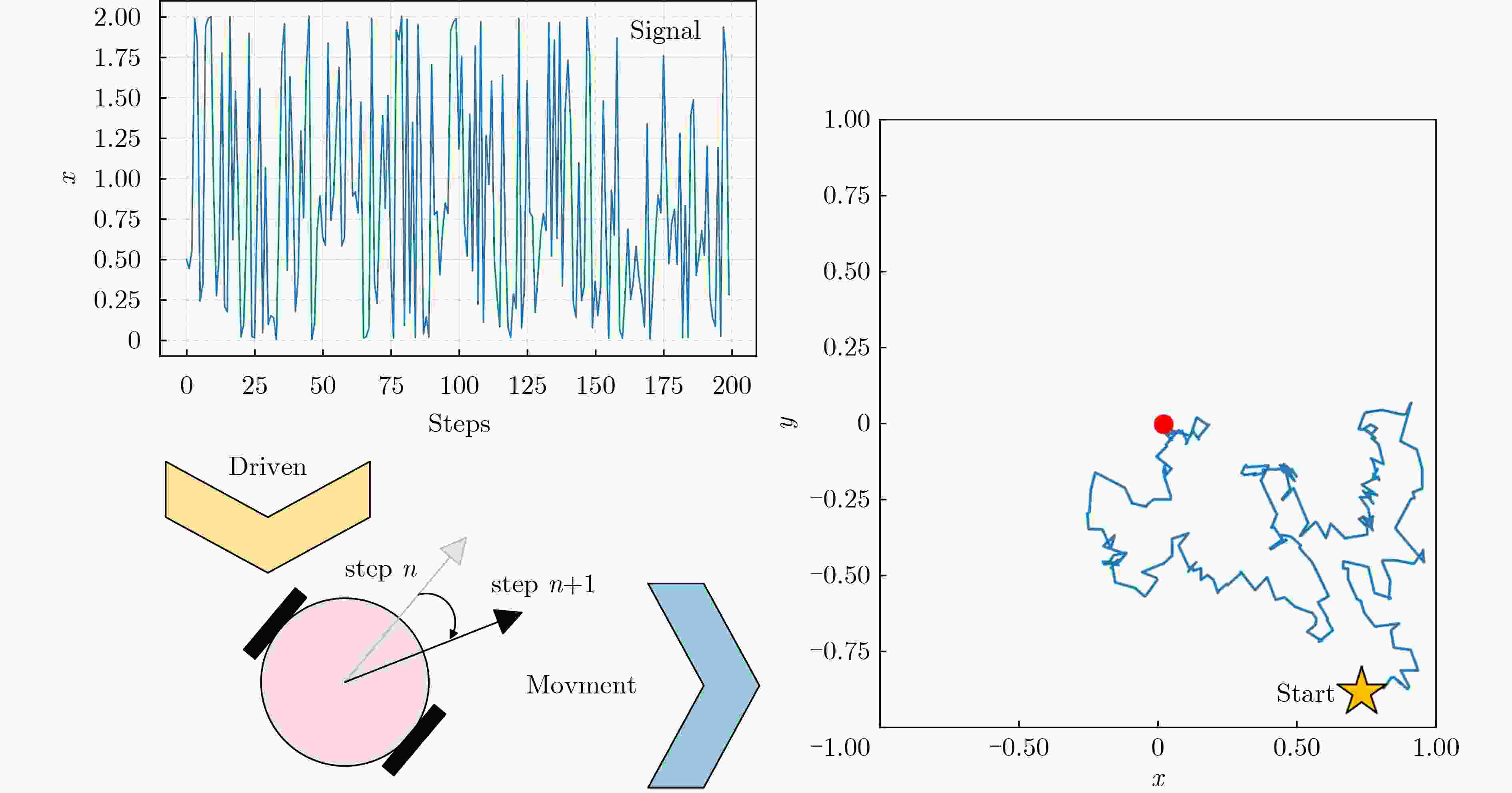
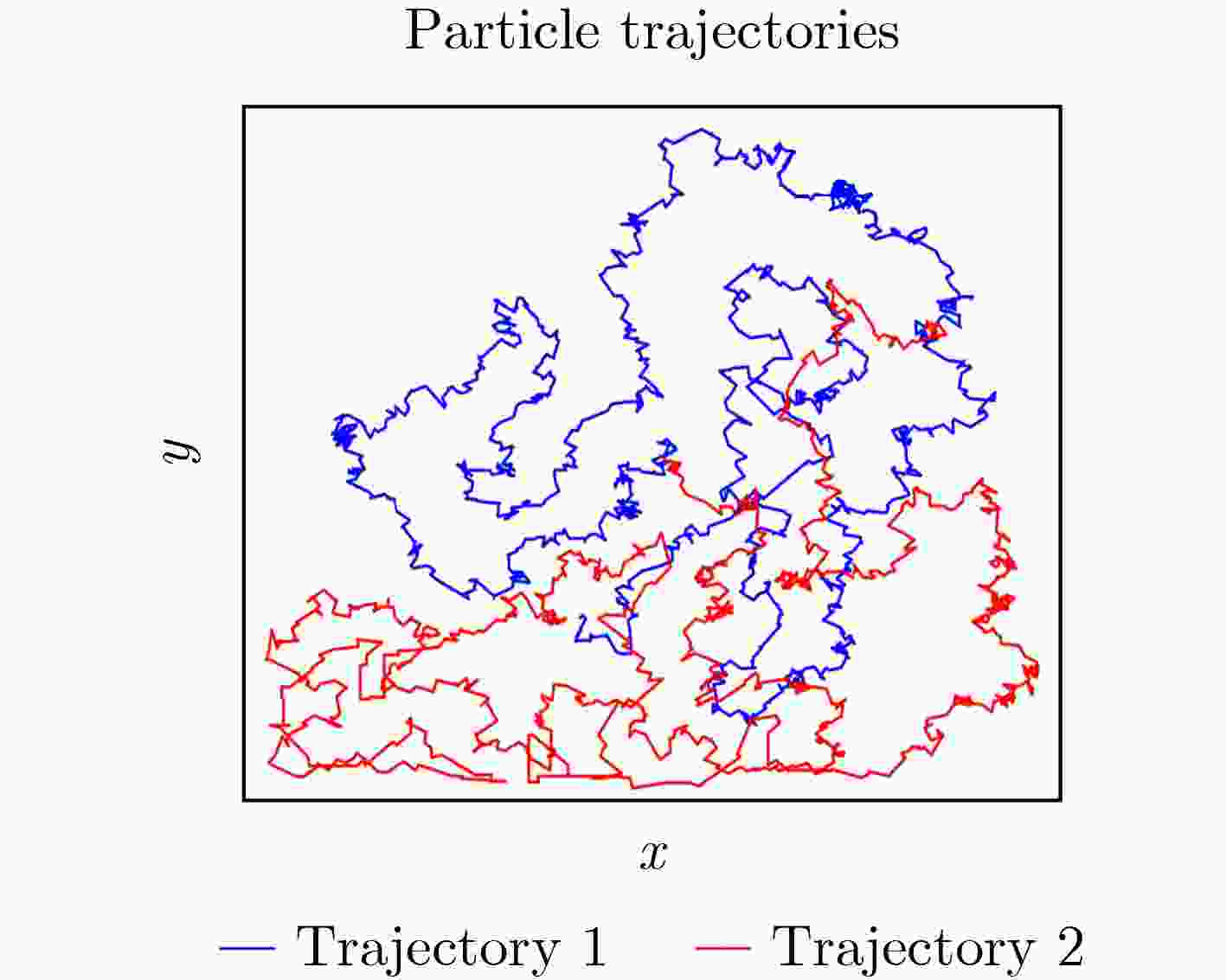
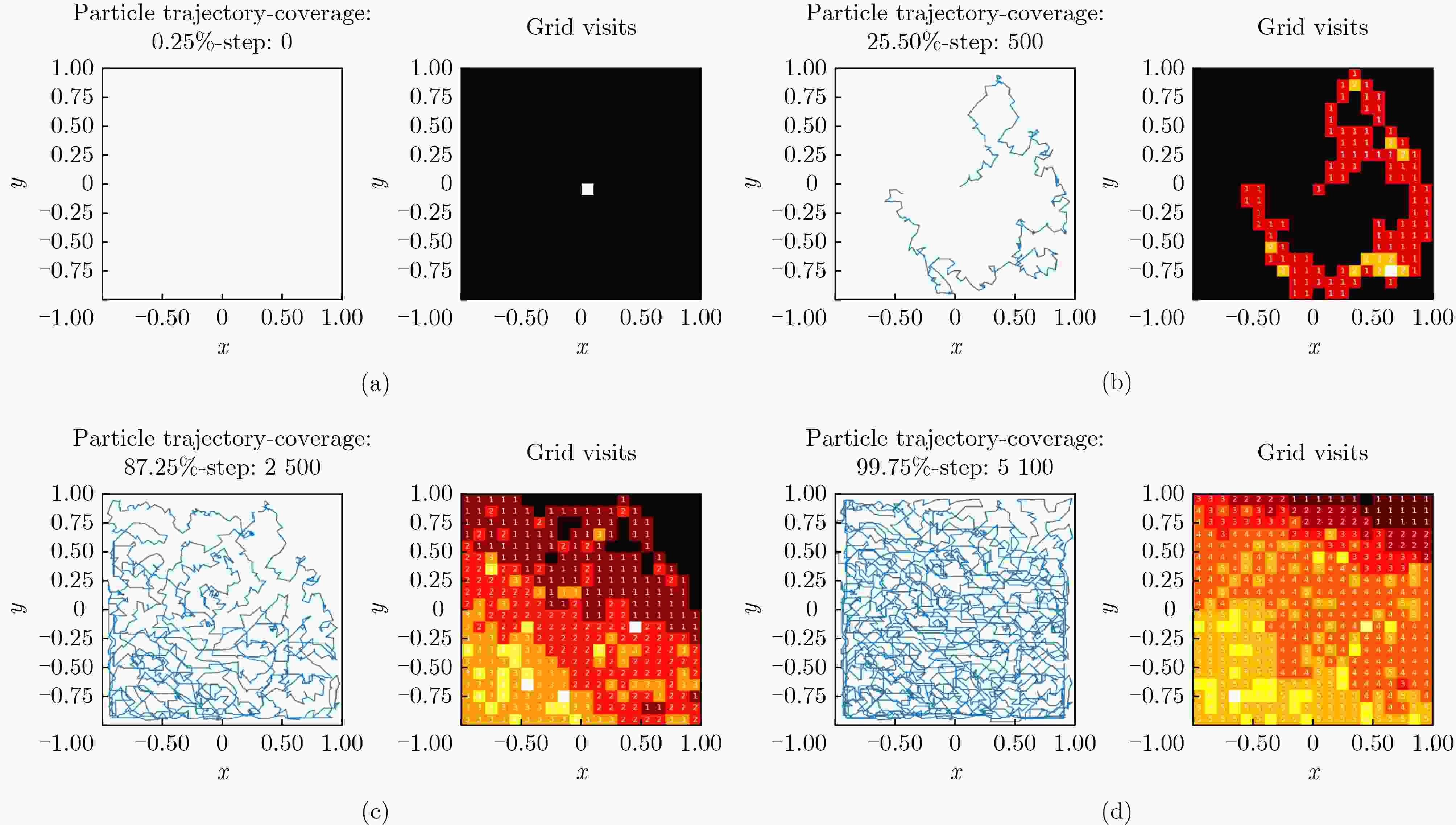
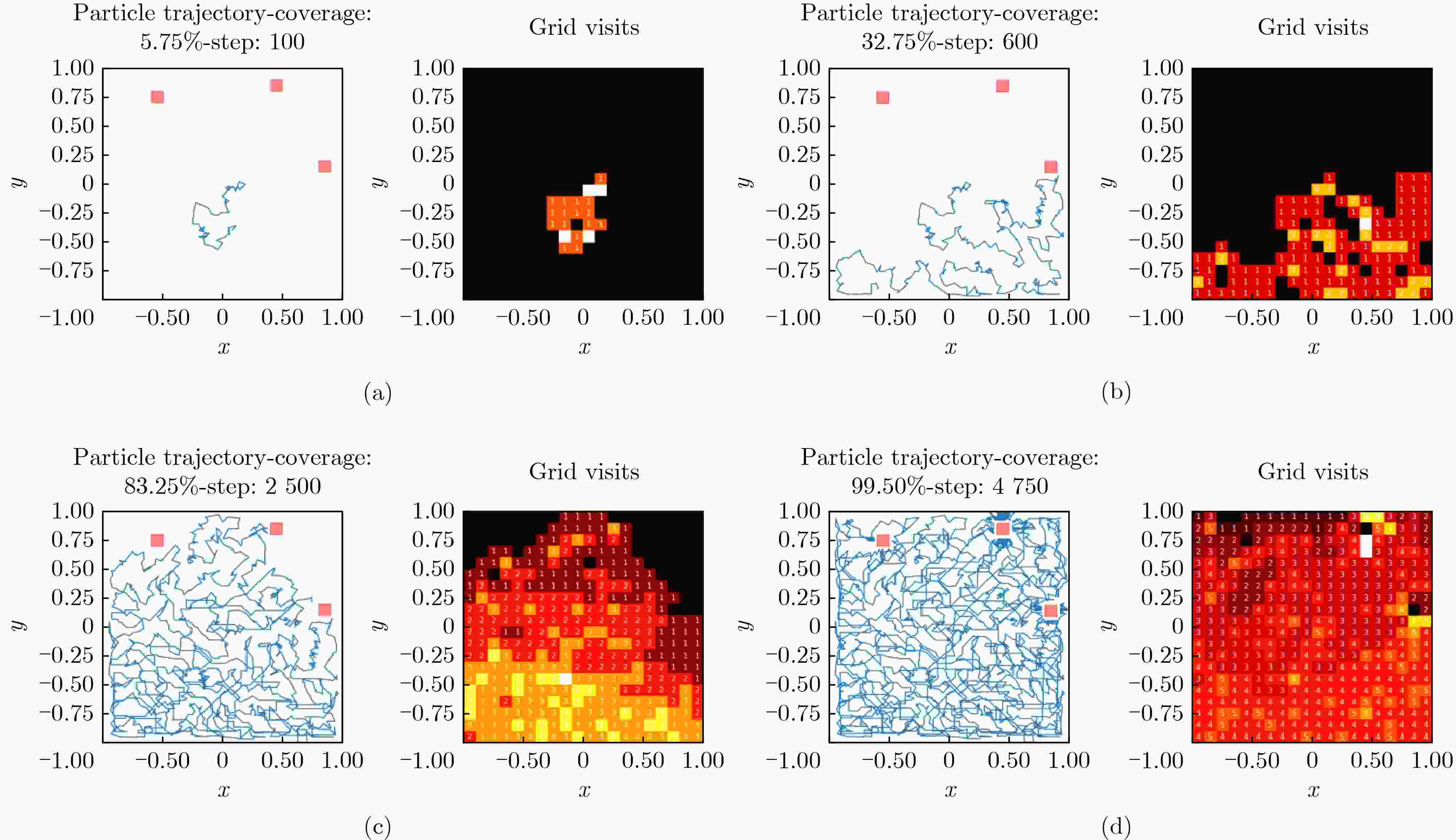
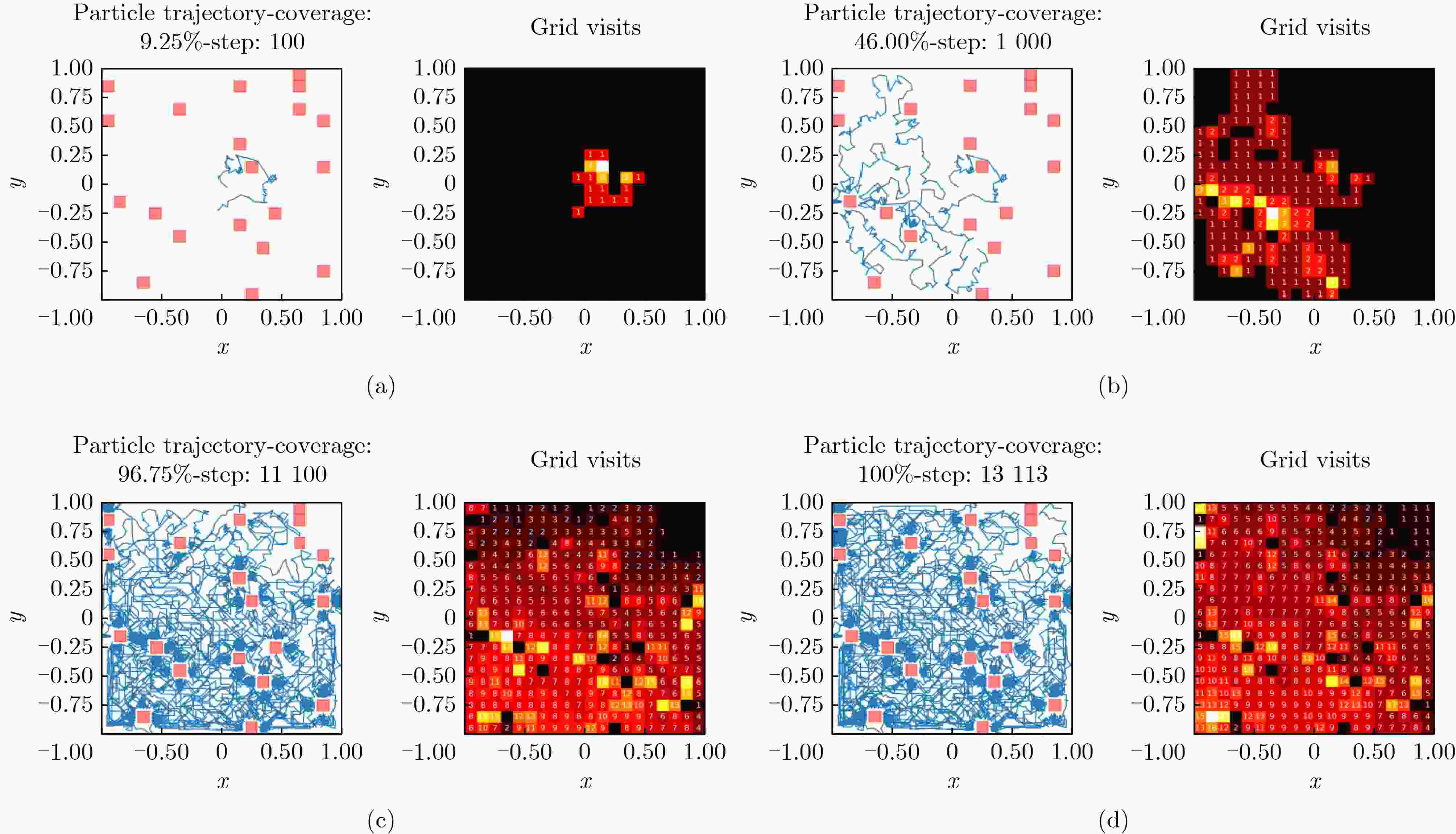
Abstract: Objective This study proposes a Complete Coverage Path Planning (CCPP) algorithm based on a sine-constrained Rulkov-Like Hyper-Chaotic (SRHC) mapping. The work addresses key challenges in robotic path planning and focuses on improving coverage efficiency, path unpredictability, and obstacle adaptability for mobile robots in complex environments, including disaster rescue, firefighting, and unknown-terrain exploration. Traditional methods often exhibit predictable movement patterns, fall into local optima, and show inefficient backtracking, which motivates the development of an approach that uses chaotic dynamics to strengthen exploration capability. Methods The SRHC-CCPP algorithm integrates three components: 1. SRHC Mapping A hyper-chaotic system with nonlinear coupling (Eq. 1) generates highly unpredictable trajectories. Lyapunov exponent analysis (Fig. 3a–b), phase-space diagrams (Fig. 1), and parameter-sensitivity studies (Table 1) confirm chaotic behavior under conditions such as a=0.01 and b=1.3. 2. Memory-Driven Exploration A dynamic visitation grid prioritizes uncovered regions and reduces redundancy (Algorithm 1). 3.Collision detection combined with normal-vector reflection reduces oscillations in cluttered environments (Fig. 4). Simulations employ a Mecanum-wheel robot model (Eq. 2) to provide omnidirectional mobility. Results and Discussions 1. Efficiency: SRHC-CCPP achieved faster coverage and improved uniformity in both obstacle-free and obstructed scenarios (Fig. 5–6). The chaotic driver increased path diversity by 37% compared with rule-based methods. 2. Robustness: The algorithm demonstrated initial-value sensitivity and adaptability to environmental noise (Table 2). 3. Scalability Its low computational overhead supported deployment in large-scale grids (>104 cells). Conclusions The SRHC-CCPP algorithm advances robotic path planning by: 1. Merging hyper-chaotic unpredictability with memory-guided efficiency, which reduces repetitive loops. 2. Offering real-time obstacle negotiation through adaptive reflection mechanics. 3. Providing a versatile framework suited to applications that require high coverage reliability and dynamic responsiveness. Future work may examine multi-agent extensions and three-dimensional environments.
- Complete coverage path planning /
- Hyper-chaotic mapping /
- Memory effect /
- Obstacle avoidance /
- Lyapunov exponent

HTML全文

图 1 系统流程示意图

下载: 全尺寸图片幻灯片

图 2 SRHC系统的相轨示意图

下载: 全尺寸图片幻灯片

图 3 SRHC系统振荡幅值变化示意图

下载: 全尺寸图片幻灯片

图 4 两轮麦克纳姆轮机器人示意图

下载: 全尺寸图片幻灯片

图 5 SRHC系统初始值敏感度分析曲线

下载: 全尺寸图片幻灯片

图 6 机器人移动轨迹示意图

下载: 全尺寸图片幻灯片

图 7 不同初始值所对应的机器人运动轨迹示意图

下载: 全尺寸图片幻灯片

图 8 无障碍条件下SRHC-CCPP算法的全覆盖路径规划快照

下载: 全尺寸图片幻灯片

图 9 稀疏障碍条件下SRHC-CCPP算法的全覆盖路径规划快照

下载: 全尺寸图片幻灯片

图 10 密集障碍条件下SRHC-CCPP算法的全覆盖路径规划快照

下载: 全尺寸图片幻灯片

1 记忆效应驱动速度调整算法

函数：记忆效应驱动速度调整
输入：网格访问计数(grid_counts)、已访问网格集(visited_grids)、当前网格(current_grid)、八邻域网格(neighbors)、当前位置　(position)、当前速度(velocity)
输出：新速度方向(new_velocity)、更新后的已访问网格集(visited_grids)、更新后的网格访问计数(grid_counts)
(1) 如果：当前网格(current_grid)未在已访问网格集(visited_grids)中：
(2) 将当前网格(current_grid)添加至已访问网格集(visited_grids)
(3) 将当前网格的访问计数(grid_counts[current_grid])加1
(4) 结束条件判断
(5) 如果：未访问邻域(unvisited_neighbors)不为空：
(6) 从非空未访问邻域(unvisited_neighbors)中随机选择目标网格(target_grid)
(7) 根据目标网格(target_grid)计算目标位置(target_position)
(8) 更新新速度方向(new_velocity)为：归一化(目标位置 - 当前位置)
(9) 否则(未访问邻域为空)：
(10) 从八邻域网格(neighbors)中筛选访问计数最小的网格(min_visit_grid)
(11) 更新新速度方向(new_velocity)为：归一化(目标位置 - 当前位置)
(12) 结束条件判断
(13) 返回新速度方向(new_velocity)、更新后的已访问网格集(visited_grids)、更新后的网格访问计数(grid_counts)

下载: 导出CSV

2 超混沌全覆盖路径规划算法实现

函数：超混沌全覆盖路径规划(SRHC-CCPP)
输入：网格数(n)、超混沌序列(chaotic_sequence)、障碍物集(obstacles)、初始位置/速度、最大角度偏差、最大迭代次数
输出：运动轨迹(trajectory)、网格访问计数(grid_counts)
(1) 初始化：当前位置=初始位置，速度归一化，角度偏差转弧度
(2) 迭代(至最大次数或覆盖率100%)：
(3) 步长=超混沌序列["y"][t]×0.01
(4) 每10步更新方向：用超混沌序列["x"][t]计算角度θ，生成旋转矩阵更新速度方向并归一化
(5) 计算新位置=当前位置+步长×速度。
(6) 边界处理：若越界，速度沿边界法线反射并叠加随机扰动，修正位置
(7) 障碍处理：若新位置含障碍，调用碰撞处理函数
(8) 网格访问优化：
(9) 计算新位置网格坐标(grid_x, grid_y)
(10) 若网格已访问：
(11) 优先选择未访问邻域网格，更新速度指向其中心
(12) 若无未访问邻域，选择访问次数最少的邻域网格，更新速度指向其中心
(13) 更新已访问网格集、网格访问计数，记录轨迹，更新当前位
(14) 返回轨迹和网格访问计数

下载: 导出CSV

表 1 全覆盖搜索步长值

序号	步长值	均值	方差
1	5013	5122.10	117.17
2	5025
3	5300
4	5005
5	5012
6	5206
7	5100
8	5120
9	5315
10	5125

下载: 导出CSV

表 2 覆盖率对比表

步长值	覆盖率 (%)
步长值	RBMCA^[¹⁰^]	M-RBMCA^[¹⁰^]	P-RBMCA^[¹⁰^]	SRHC-CCPP
1000	4.16	4.18	7.16	48.25
2500	9.67	10	19.6	87.25
5000	19.93	20.13	38.67	99.75
7500	29.54	30.07	54.09	100
10000	35.01	35.46	71.03	100

下载: 导出CSV

表 3 全覆盖搜索步长值

序号	步长值	均值	方差
1	5213	5269.30	146.46
2	5125
3	5500
4	5205
5	5112
6	5366
7	5500
8	5128
9	5319
10	5225

下载: 导出CSV

表 4 全覆盖搜索步长值

序号	步长值	均值	方差
1	13113	14214	980.04
2	15125
3	15523
4	15202
5	14115
6	14366
7	12598
8	13168
9	14310
10	14620

下载: 导出CSV

参考文献(31)

[1]	AHURAKA F, MCNAMEE P, WANG Qixu, et al. Chaotic motion planning for mobile robots: Progress, challenges, and opportunities[J]. IEEE Access, 2023, 11: 134917–134939. doi: 10.1109/ACCESS.2023.3337371.
[2]	SHIVASHANKAR V, JAIN R, KUTER U, et al. Real-time planning for covering an initially-unknown spatial environment[C]. The Twenty-Fourth International Florida Artificial Intelligence Research Society Conference, Palm Beach, USA, 2011: 63–68.
[3]	GRØTLI E I and JOHANSEN T A. Path planning for UAVs under communication constraints using SPLAT! And MILP[J]. Journal of Intelligent & Robotic Systems, 2012, 65(1/4): 265–282. doi: 10.1007/s10846-011-9619-8.
[4]	YAN Mingzhong and ZHU Daqi. An algorithm of complete coverage path planning for autonomous underwater vehicles[J]. Key Engineering Materials, 2011, 467/469: 1377–1385. doi: 10.4028/www.scientific.net/KEM.467-469.1377.
[5]	HERT S, TIWARI S, and LUMELSKY V. A terrain-covering algorithm for an AUV[M]. YUH J, URA T, and BEKEY G A. Underwater Robots. New York, USA: Springer, 1996: 17–45. doi: 10.1007/978-1-4613-1419-6_2.
[6]	PANG Bao, SONG Yong, ZHANG Chengjin, et al. A swarm robotic exploration strategy based on an improved random walk method[J]. Journal of Robotics, 2019, 2019: 6914212. doi: 10.1155/2019/6914212.
[7]	PANG Bao, QI Jiahui, ZHANG Chengjin, et al. Analysis of random walk models in swarm robots for area exploration[C]. 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 2019: 2484–2489. doi: 10.1109/ROBIO49542.2019.8961844.
[8]	PETAVRATZIS E, MOYSIS L, VOLOS C, et al. A chaotic path planning generator enhanced by a memory technique[J]. Robotics and Autonomous Systems, 2021, 143: 103826. doi: 10.1016/j.robot.2021.103826.
[9]	MOYSIS L, PETAVRATZIS E, VOLOS C, et al. A chaotic path planning generator based on logistic map and modulo tactics[J]. Robotics and Autonomous Systems, 2020, 124: 103377. doi: 10.1016/j.robot.2019.103377.
[10]	KVITKO D, RYBIN V, BAYAZITOV O, et al. Chaotic path-planning algorithm based on Courbage–Nekorkin artificial neuron model[J]. Mathematics, 2024, 12(6): 892. doi: 10.3390/math12060892.
[11]	SRIDHARAN K and AHMADABADI Z N. A multi-system chaotic path planner for fast and unpredictable online coverage of terrains[J]. IEEE Robotics and Automation Letters, 2020, 5(4): 5268–5275. doi: 10.1109/LRA.2020.3007471.
[12]	NASR S, MEKKI H, and BOUALLEGUE K. A multi-scroll chaotic system for a higher coverage path planning of a mobile robot using flatness controller[J]. Chaos, Solitons & Fractals, 2019, 118: 366–375. doi: 10.1016/j.chaos.2018.12.002.
[13]	ROSALIE M, DANOY G, CHAUMETTE S, et al. Chaos-enhanced mobility models for multilevel swarms of UAVs[J]. Swarm and Evolutionary Computation, 2018, 41: 36–48. doi: 10.1016/j.swevo.2018.01.002.
[14]	GAO Mingsheng, LIU Yuxiang, and WEI Pengfei. Opposite and chaos searching genetic algorithm based for UAV path planning[C]. The 6th IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 2020: 2364–2369. doi: 10.1109/ICCC51575.2020.9345125.
[15]	VESLIN DIAZ E, SLAMA J, DUTRA M, et al. Trajectory tracking for robot manipulators using differential flatness[J]. Ingeniería e Investigación, 2011, 31(2): 84–90. doi: 10.15446/ing.investig.v31n2.23468.
[16]	LEVINE J. Analysis and Control of Nonlinear Systems: A Flatness-Based Approach[M]. Berlin, Heidelberg, Germany: Springer, 2009: 110-134. doi: 10.1007/978-3-642-00839-9.
[17]	MARKUS E D, AGEE J T, JIMOH A A, et al. Flatness based control of a 2 DOF single link flexible joint manipulator[C].The 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications - SIMULTECH, Rome, Italy, 2012: 437–442. doi: 10.5220/0004061104370442.
[18]	MARKUS E D, AGEE J T, and JIMOH A A. Flat control of industrial robotic manipulators[J]. Robotics and Autonomous Systems, 2017, 87: 226–236. doi: 10.1016/j.robot.2016.10.009.
[19]	AL-RAEEI M. Applying fractional quantum mechanics to systems with electrical screening effects[J]. Chaos, Solitons & Fractals, 2021, 150: 111209. doi: 10.1016/j.chaos.2021.111209.
[20]	SEADAWY A R, ALI S, and RIZVI S T R. On modulation instability analysis and rogue waves in the presence of external potential: The (n + 1)-dimensional nonlinear Schrödinger equation[J]. Chaos, Solitons & Fractals, 2022, 161: 112374. doi: 10.1016/j.chaos.2022.112374.
[21]	RYBIN V, BUTUSOV D, BABKIN I, et al. Some properties of a discrete Lorenz system obtained by variable midpoint method and its application to chaotic signal modulation[J]. International Journal of Bifurcation and Chaos, 2024, 34(1): 2450009. doi: 10.1142/S0218127424500093.
[22]	CIRJULINA D, BABAJANS R, CAPLIGINS F, et al. Experimental study on Colpitts chaotic oscillator-based communication system application for the internet of things[J]. Applied Sciences, 2024, 14(3): 1180. doi: 10.3390/app14031180.
[23]	CHO S W, PARK H J, LEE H, et al. Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations[J]. Computers & Industrial Engineering, 2021, 161: 107612. doi: 10.1016/j.cie.2021.107612.
[24]	LUIS S Y, PERALTA F, CÓRDOBA A T, et al. An evolutionary multi-objective path planning of a fleet of ASVs for patrolling water resources[J]. Engineering Applications of Artificial Intelligence, 2022, 112: 104852. doi: 10.1016/j.engappai.2022.104852.
[25]	DOLGUI A, SGARBOSSA F, and SIMONETTO M. Design and management of assembly systems 4.0: systematic literature review and research agenda[J]. International Journal of Production Research, 2022, 601: 184-210. doi: 10.1080/00207543.2021.1990433.
[26]	LIAN Jianfang, YU Wentao, XIAO Kui, et al. Cubic spline interpolation-based robot path planning using a chaotic adaptive particle swarm optimization algorithm[J]. Mathematical Problems in Engineering, 2020, 2020: 1849240. doi: 10.1155/2020/1849240.
[27]	SHAO Shikai, PENG Yu, HE Chenglong, et al. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization[J]. ISA Transactions, 2020, 97: 415–430. doi: 10.1016/j.isatra.2019.08.018.
[28]	MOYSIS L, VOLOS C, PHAM V T, et al. Analysis of a hyperchaotic system with a hyperbolic sinusoidal nonlinearity and its application to area exploration using multiple autonomous robots[M]. VOLCHENKOV D and LUO A C J. New Perspectives on Nonlinear Dynamics and Complexity. Cham, Switzerland: Springer, 2023: 43–62. doi: 10.1007/978-3-030-97328-5_4.
[29]	LE A V, VO D T, DAT N T, et al. Complete coverage planning using deep reinforcement learning for polyiamonds-based reconfigurable robot[J]. Engineering Applications of Artificial Intelligence, 2024, 138: 109424. doi: 10.1016/j.engappai.2024.109424.
[30]	CHEN Bolei, ZHONG Ping, CUI Yongzheng, et al. EMExplorer: An episodic memory enhanced autonomous exploration strategy with Voronoi domain conversion and invalid action masking[J]. Complex & Intelligent Systems, 2023, 9(6): 7365–7379. doi: 10.1007/s40747-023-01144-x.
[31]	LI Jianyu, WANG Kezhi, CHEN Zonghai, et al. An improved RRT* path planning algorithm in dynamic environment[C]. The 21st Asian Simulation Conference on Methods and Applications for Modeling and Simulation of Complex Systems, Changsha, China, 2022: 301–313. doi: 10.1007/978-981-19-9195-0_25.