Optimization of Short Packet Communication Resources for UAV Assisted Power Inspection
-
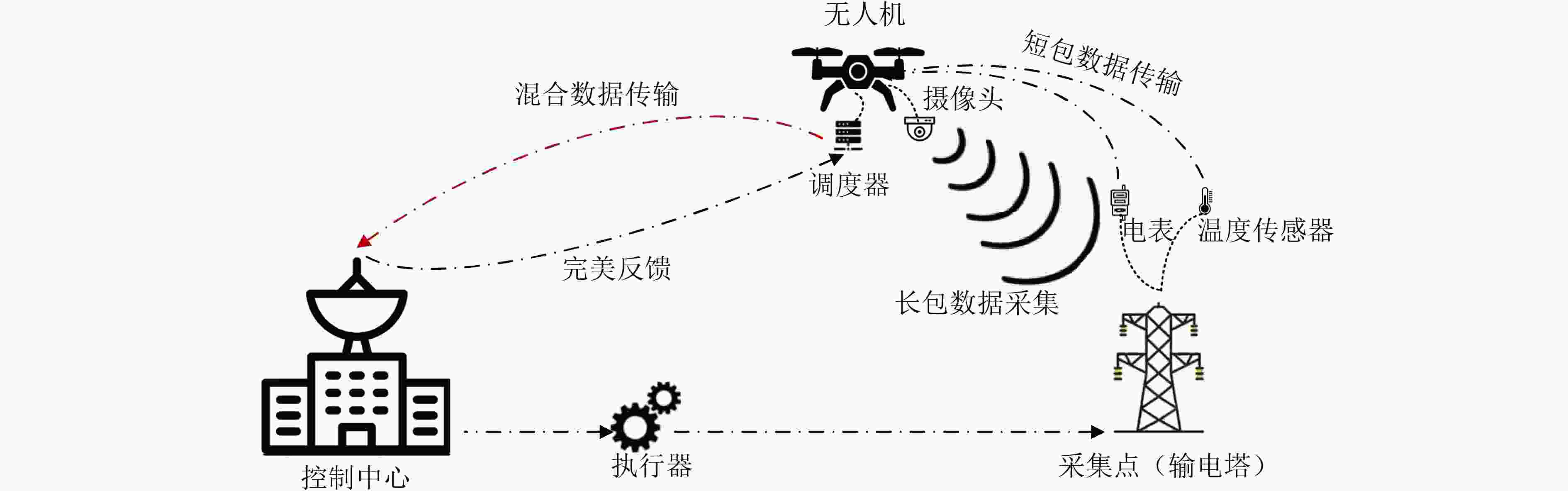
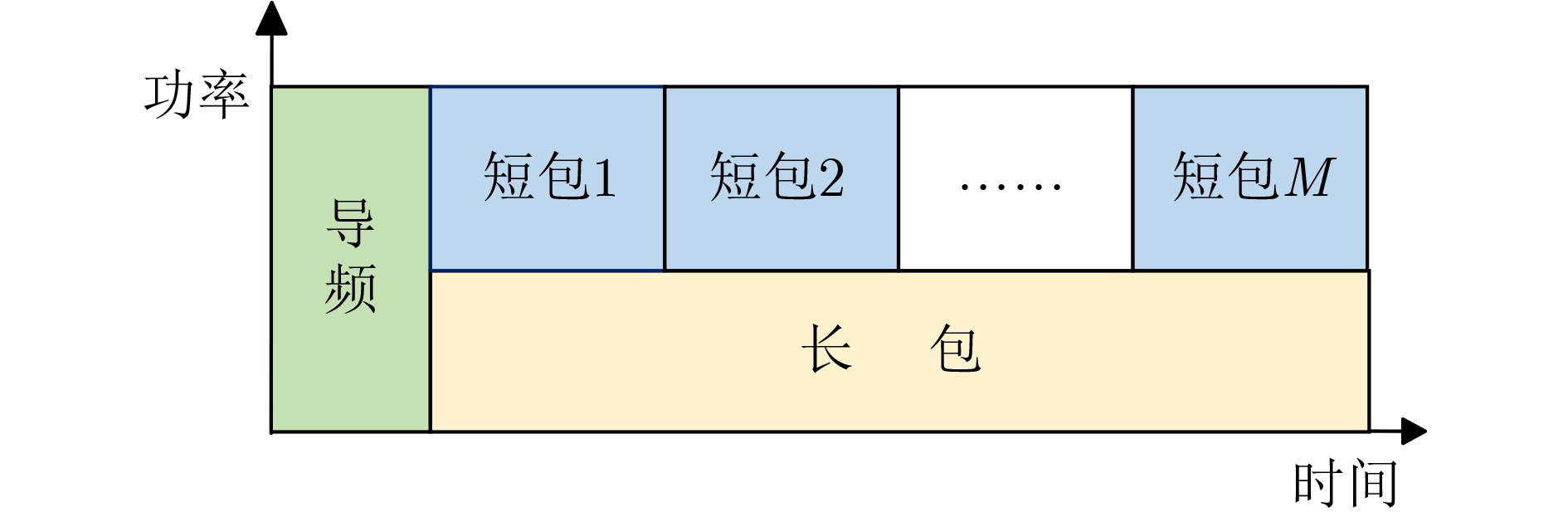
摘要: 在无人机辅助电力巡检场景中，为保障电网安全运行，无人机需实时采集并回传电网关键状态参数和图像、视频等多模态数据，控制中心基于此对电网进行调度与调控。无人机巡检任务中的数据采集与回传具有超可靠低时延和实时大带宽等通信需求。然而，无线通信资源的稀缺性和无人机能量约束使得上述异构需求难满足，进而导致巡检数据的时效性和巡检任务的有效性难保障。针对上述挑战，该文提出了数据传输调度与通信资源分配的协同优化算法，在任务性能与约束下，降低系统开销，并基于非正交多址接入技术设计长短包混合帧结构，满足异构通信需求。在无人机数据传输调度方面，将调度决策建模为马尔可夫决策过程，并将通信消耗纳入决策成本。在通信资源优化方面，联合优化长短包功率配置、短包包长和导频长度，进而在保障长包传输需求的前提下，提升短包传输的可靠性，满足异构通信需求，实现低开销的无人机电力巡检策略。仿真结果表明，该方法能够在保障传输可靠性的同时，显著降低通信成本，为无人机辅助电力巡检场景中的异构数据传输提供有效支撑。Abstract:
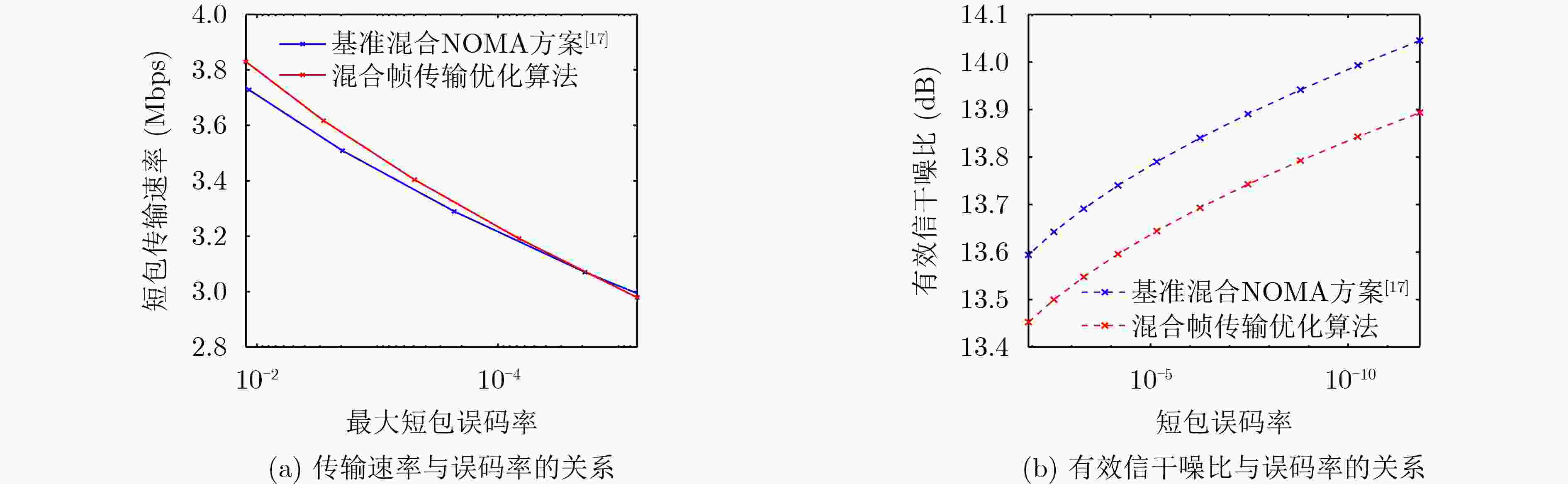
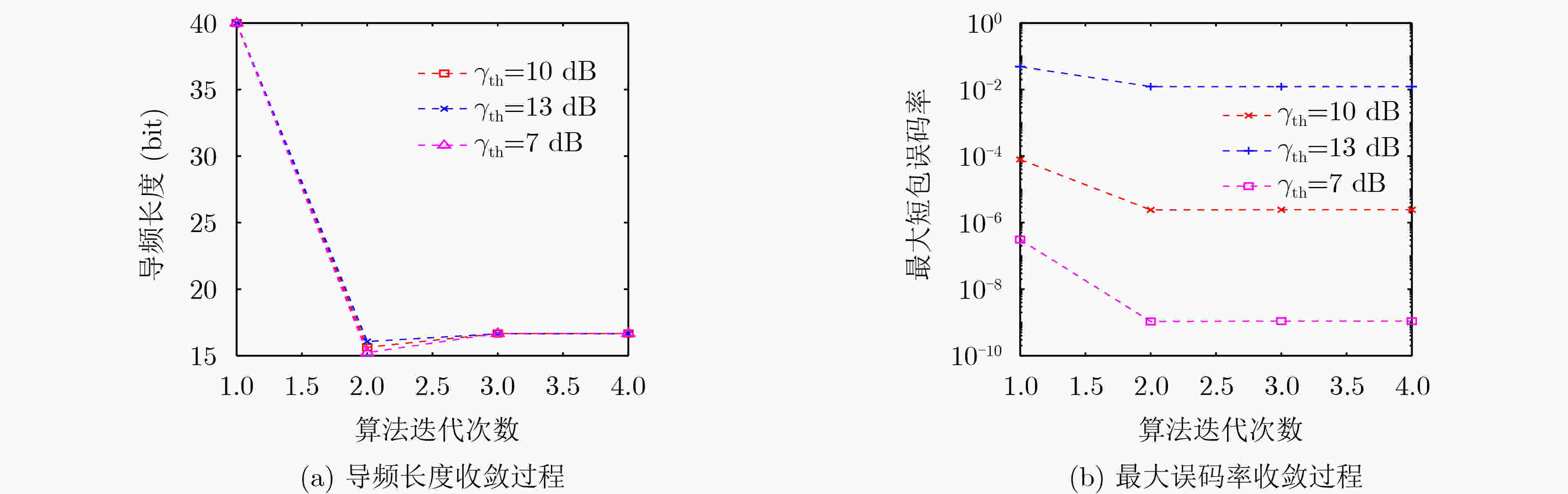
Objective In Unmanned Aerial Vehicle (UAV)–assisted power grid inspection, the real-time acquisition and transmission of multi-modal data (key parameters, images, and videos) are essential for secure grid operation. These tasks require heterogeneous communication conditions, including ultra-reliable low-latency transmission and high-bandwidth data delivery. The limited wireless communication resources and UAV energy constraints restrict the ability to meet these conditions and reduce data timeliness and task performance. The present study is designed to establish a collaborative optimization framework for transmission scheduling and communication resource allocation, ensuring minimal system overhead while meeting task performance and reliability requirements. Methods To address the challenges mentioned above, a collaborative optimization framework is established for data transmission scheduling and communication resource allocation. Data transmission scheduling is formulated as a Markov Decision Process (MDP), in which communication consumption is incorporated into the decision cost. At the resource allocation level, Non-Orthogonal Multiple Access (NOMA) technology is applied to increase spectral efficiency. This approach reduces communication cost, maintains transmission reliability, and supports heterogeneous data transmission requirements in UAV-assisted power inspection. Results and Discussions The effectiveness of the proposed framework is verified through comprehensive simulations. A scenario is established in which the UAV is required to collect data from multiple distributed power towers within a designated area. A trade-off is observed between reliability and transmission speed (Fig. 3). At the same transmission rate, the bit error rate is reduced by approximately one order of magnitude. When a minimum long-packet signal-to-noise ratio threshold of 7 dB is applied, the optimized transmission system reduces the bit error rate from the 10–3 level to the 10–5 level while requiring only about a 0.4 Mbps decrease in transmission rate. After algorithm optimization, a lower effective signal-to-noise ratio is needed to achieve the same bit error rate; under the same signal-to-noise ratio, the short-packet error performance is improved, indicating more stable system behavior and higher transmission efficiency ( Fig. 4 ).Conclusions This study presents a collaborative optimization framework that addresses the challenges posed by limited communication resources and heterogeneous data transmission requirements in UAV power inspection. By integrating MDP-based adaptive scheduling with NOMA-based joint resource allocation, the framework maintains an appropriate balance between communication performance and system overhead. The findings provide a theoretical and practical foundation for efficient, low-cost, and reliable data transmission in future intelligent autonomous aerial systems. -
1 无人机数据传输调度算法表
输入：状态$ {s_k} $，动作$ {a_k} $，状态转移概率$ P\left\langle {{{s_k}}} \mathrel{\left | {\vphantom {{{s_k}} {{s_{k - 1}},{a_{k - 1}}}}} \right. } {{{s_{k - 1}},{a_{k - 1}}}} \right\rangle $，AoI阈值$ {\varDelta _{{\text{thr}}}} $，语义匹配度阈值$ \zeta $，通信成本${l_k}$，折扣因子$\upsilon \in [0,1)$，收敛
阈值$\varsigma $；输出：调度矩阵${\boldsymbol{\varPi}} $； 1：初始化值函数${V^0}({s_k}) = 1$，${V^1}({s_k}) = 0$，迭代轮次$i = 1$； 2 //值迭代主循环 3： repeat 4： 初始化：$i = i + 1$，${V^i}({s_k}) = {V^{i + 1}}({s_k})$，$\delta = 0$ 5： for每个时隙状态${s_k}$ do 6： 计算动作价值函数：$ Q({s_k},{a_k}) = {l_k} + \upsilon \cdot \sum\limits_{{s_k}} {P({s_k}|{s_{k - 1}},{a_k})V({s_k})} \} $ 7： 更新值函数：$V({s_k}) = \min \{ Q({s_k},0),Q({s_k},1)\} $ 8： $\delta = \max \{ \delta ,\left| {{V^i}({s_k}) - {V^{i - 1}}({s_k})} \right|$ 9： end for 10：Until $\delta $<$\varsigma $ 11：//策略提取阶段 12：for 每个时隙状态${s_k}$ do 13： 得出最优策略$ \pi *({s_k}) = \mathop {\arg \min }\limits_{{a_k} \in \{ 0,1\} } \{ {l_k} + \upsilon \cdot \sum\limits_{{s_k}} {P\left\langle {{{s_k}}} \mathrel{\left | {\vphantom {{{s_k}} {{s_{k - 1}},0}}} \right. } {{{s_{k - 1}},0}} \right\rangle V({s_k})} \} $ 14：end for 15：return $\pi *$ 
下载: 导出CSV
2 基于NOMA的混合帧结构传输优化算法
输入：长包信噪比门限${\gamma _{{\text{th}}}}$，总功率限制${P_{\max }}$，短包信息比特数
$L$，最长帧长${N_{\max }}$，算法收敛阈值$\theta $。(1) 短包关联矩阵${\varPhi _1}$，功率分配$P_1^{\rm S},P_1^{\rm L}$，短包长度${N_{{{\mathrm{S}}_1}}}$，导
频长度${N_{{{\mathrm{P}}_1}}}$，迭代轮次$r = 1$。(2) 重复步骤(3)～(6)直到满足$\left| {{\eta _r} - {\eta _{r - 1}}} \right| < \theta $。 (3) 已知${N_{{{\mathrm{p}}_{r - 1}}}},{N_{{{\mathrm{S}}_{r - 1}}}},P_{r - 1}^{\rm S},P_{r - 1}^{\rm L}$求解优化问题${\text{P2}}{\text{.1}}$，得到
${\varPhi _r}$。(4) 已知${\varPhi _r},P_r^{\rm S},P_r^{\rm L}$，求解优化问题${\text{P2}}{\text{.2}}$，得到${N_{{{\mathrm{P}}_r}}},{N_{{{\mathrm{S}}_r}}}$。 (5) 已知${\varPhi _r},{N_{{{\mathrm{p}}_r}}},{N_{{{\mathrm{S}}_r}}}$求解优化问题${\text{P2}}{\text{.3}}$，得到$P_r^{\rm S},P_r^{\rm L}$。 (6) 得到${\eta _r}$，更新迭代次数$r = r + 1$ (7) 结束并输出。 输出：短包关联矩阵$\varPhi $，功率分配${P^{\rm S}},{P^{\rm L}}$，短包长度${N_{\mathrm{S}}}$，导频
长度${N_{\mathrm{P}}}$。
下载: 导出CSV
表 1 仿真参数设置表
参数 数值 混合帧结构最长帧长${N_{\max }}$ 800 bit 每帧结构携带短包数$M$ 10 长包信噪比门限${\gamma _{{\text{th}}}}$ [5, 13] dB 短包信息比特数$L$ [150, 300] bit 传输总功率限制${P_{\max }}$ 1 W 总带宽$B$ 1 MHz 噪声功率谱密度${N_0}$ –170 dBm/Hz 状态转移概率$P$ 0.4 两种环境条件下的频移阈值$ {\zeta _0} $, $ {\zeta _1} $ 0.10 Hz, 0.01 Hz 折扣因子$\upsilon $ 0.95
下载: 导出CSV
-
[1] CAO Lei and WANG Huai. Research on UAV network communication application based on 5G technology[C]. 2022 3rd International Conference on Electronic Communication and Artificial Intelligence (IWECAI), Zhuhai, China, 2022: 125–129. doi: 10.1109/IWECAI55315.2022.00033. [2] DIAO Xianbang, CAI Yueming, YU Baoquan, et al. Location and complex status update strategy optimization in UAV-assisted IoT[J]. IEEE Internet of Things Journal, 2023, 10(13): 11588–11604. doi: 10.1109/JIOT.2023.3244541. [3] KAUL S, YATES R, and GRUTESER M. Real-time status: How often should one update?[C]. 2012 IEEE INFOCOM, Orlando, USA, 2012: 2731–2735. doi: 10.1109/INFCOM.2012.6195689. [4] ZHANG X, CHANG Z, HÄMÄLÄINEN T, et al. AoI-energy tradeoff for data collection in UAV-assisted wireless networks[J]. IEEE Transactions on Communications, 2024, 72(3): 1849–1861. doi: 10.1109/TCOMM.2023.3337400. [5] HUANG Xiong and FU Xiuwen. Fresh data collection for UAV-assisted IoT based on aerial collaborative relay[J]. IEEE Sensors Journal, 2023, 23(8): 8810–8825. doi: 10.1109/JSEN.2023.3253920. [6] NG B K, LAM C T, and LAW E K L. Blocklength minimization in NOMA systems with hybrid long and short packets[C]. 2021 IEEE Latin-American Conference on Communications (LATINCOM), Santo Domingo, Dominican Republic, 2021: 1–5. doi: 10.1109/LATINCOM53176.2021.9647829. [7] ZENG Haiyong, ZHANG Rui, ZHU Xu, et al. Frame structure and resource optimization for hybrid NOMA-based data collection in IIoT with imperfect SIC[J]. IEEE Internet of Things Journal, 2024, 11(23): 37799–37812. doi: 10.1109/JIOT.2024.3444462. [8] CAO jie, KURNIAWAN Ernest, BOONKAJAY Amnart. Goal-Oriented Integration of Sensing, Communication, Computing, and Control for Mission-Critical Internet-of-Things[J]. IEEE Network, 2024, 38(6): 13–20 doi: 10.1109/MNET.2024.3414396. [9] VILNI S S, MOLTAFET M, LEINONEN M, et al. Multi-source AoI-constrained resource minimization under HARQ: Heterogeneous sampling processes[J]. IEEE Transactions on Vehicular Technology, 2024, 73(1): 1084–1099. doi: 10.1109/TVT.2023.3310190. [10] CHEN He, GU Yifan, and LIEW S C. Age-of-information dependent random access for massive IoT networks[C]. The IEEE INFOCOM 2020 - IEEE Conference on Computer Communications Workshops, Toronto, Canada, 2020: 930–935. doi: 10.1109/INFOCOMWKSHPS50562.2020.9162973. [11] QIN Meng, CHENG Nan, JING Zewei, et al. Service-oriented energy-latency tradeoff for IoT task partial offloading in MEC-enhanced multi-RAT networks[J]. IEEE Internet of Things Journal, 2021, 8(3): 1896–1907. doi: 10.1109/JIOT.2020.3015970. [12] WANG Kunlun, NIYATO D, CHEN Wen, et al. Task-oriented delay-aware multi-tier computing in cell-free massive MIMO systems[J]. IEEE Journal on Selected Areas in Communications, 2023, 41(7): 2000–2012. doi: 10.1109/JSAC.2023.3280965. [13] CAO Jie, ZHU Xu, JIANG Yufei, LIU Yujie, WEIZhongxiang, SUN Sumei, ZHENG Fu-Chun, et al. Independent Pilots Versus Shared Pilots: ShortFrameStructure Optimization for Heterogeneous-TrafficURLLCNetworks[J]. IEEE Transactions onWirelessCommunications, 2022, 21(8): 5755–5769 doi: 10.1109/TWC.2022.3143002. [14] POLYANSKIY Y, POOR H V, and VERDU S. Channelcoding rate in the finite blocklength regime[J]. IEEETransactions on Information Theory, 2010, 56(5): 2307–2359 doi: 10.1109/TIT.2010.2043769. [15] JINDAL N and LOZANO A. A unified treatment of optimum pilot overhead in multipath fading channels[J]. IEEE Transactions on Communications, 2010, 58(10): 2939–2948 doi: 10.1109/TCOMM.2010.083110.090696. [16] CAO Jie, KURNIAWAN Ernest, BOONKAJAY Amnart, PAPPAS Nikolaos, SUN Sumei, POPOVSKI Petar, et al. Goal-Oriented Communication, Estimation, and Control Over Bidirectional Wireless Links[J]. IEEE Transactions on Communications, 2025, 73(5): 3031–3045 doi: 10.1109/TCOMM.2024.3485572. [17] LAI Xiazhi, ZHANG Qi, and QIN Jiayin. Downlink NOMA networks with hybrid long-packet and short-packet communications in flat Rayleigh fading channels[J]. IEEE Systems Journal, 2020, 14(3): 3410–3413. doi: 10.1109/JSYST.2019.2931843. -
图(5) / 表(3)
计量
- 文章访问数: 93
- HTML全文浏览量: 28
- PDF下载量: 38
- 被引次数: 0
下载:
