3D Localization Method with Uniform Circular Array Driven by Complex Subspace Neural Network
-
摘要: 针对复杂室内环境中由频率偏移、多径传播以及噪声干扰等因素导致定位精度不足的问题,该文提出一种复数子空间神经网络(CSNN)驱动的均匀圆阵三维定位方法。首先,构建基于信号参考周期与采样周期的双估计频率补偿算法。通过预估计对精估计的频率模糊进行修正,以获得精确的频偏值实现频率补偿。其次,提出基于复数子空间神经网络的二维角度估计算法。利用复数卷积神经网络(CVCNN)重构信号协方差矩阵,抑制非主径分量与噪声的影响,恢复信号与噪声子空间的正交性,并利用模式空间转换与子空间算法实现高精度二维角度估计。在此基础上,设计了基于均匀圆阵的原型系统进行实验。结果表明,该方法在跨场景迁移后二维与三维定位的平均误差分别为28.9 cm和36.5 cm,验证了所提方法的定位精度与泛化能力。Abstract:
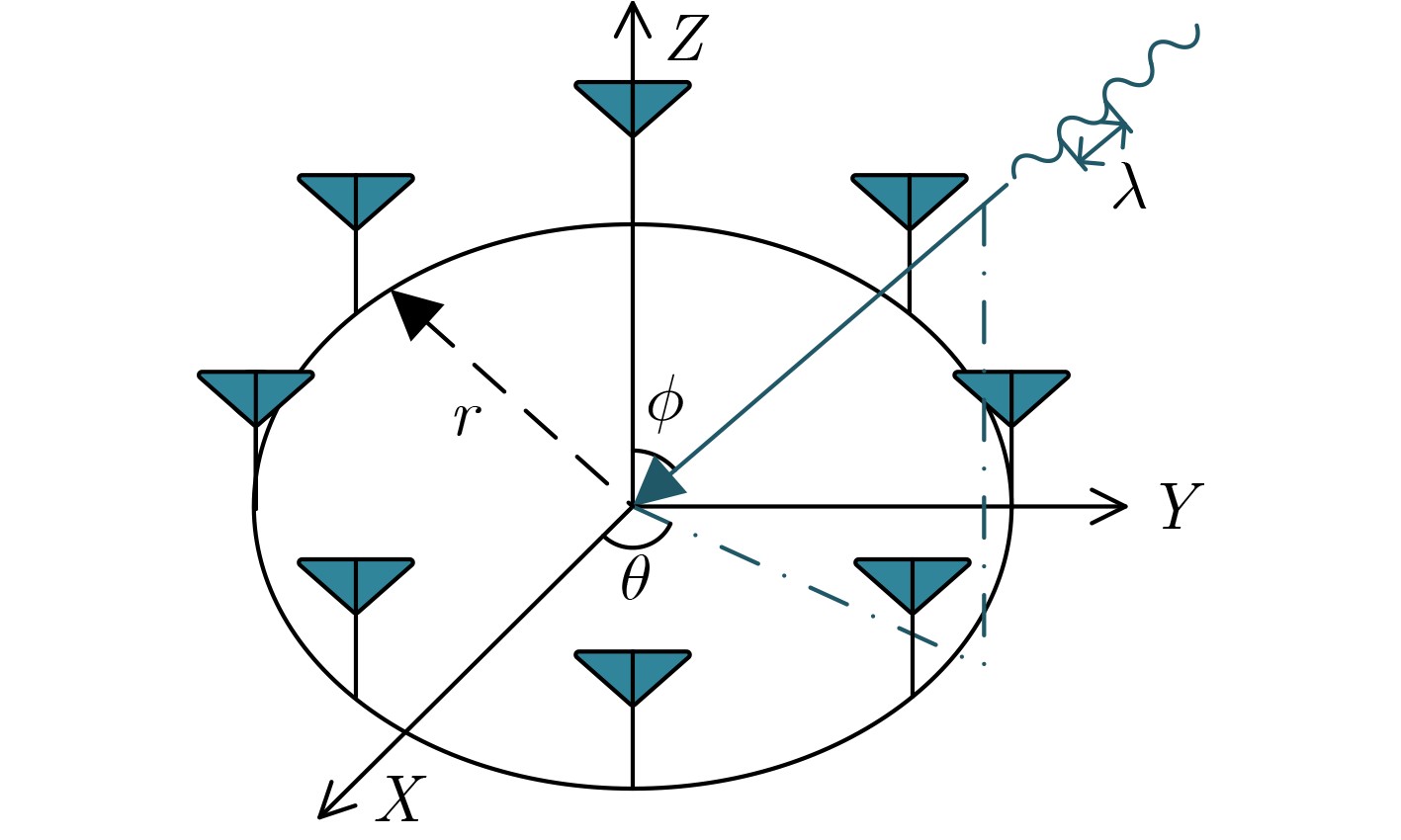
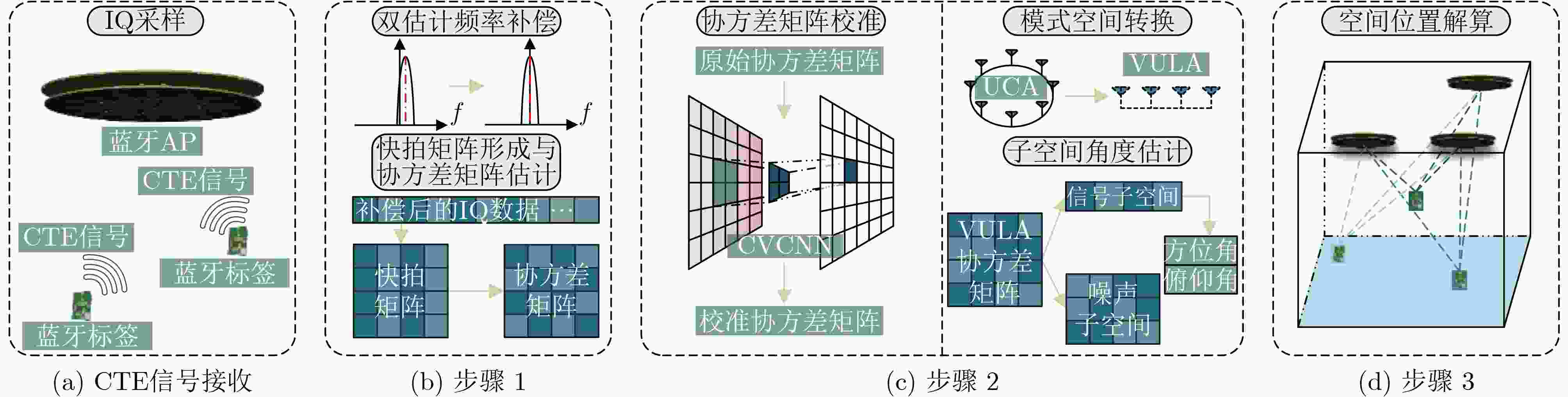
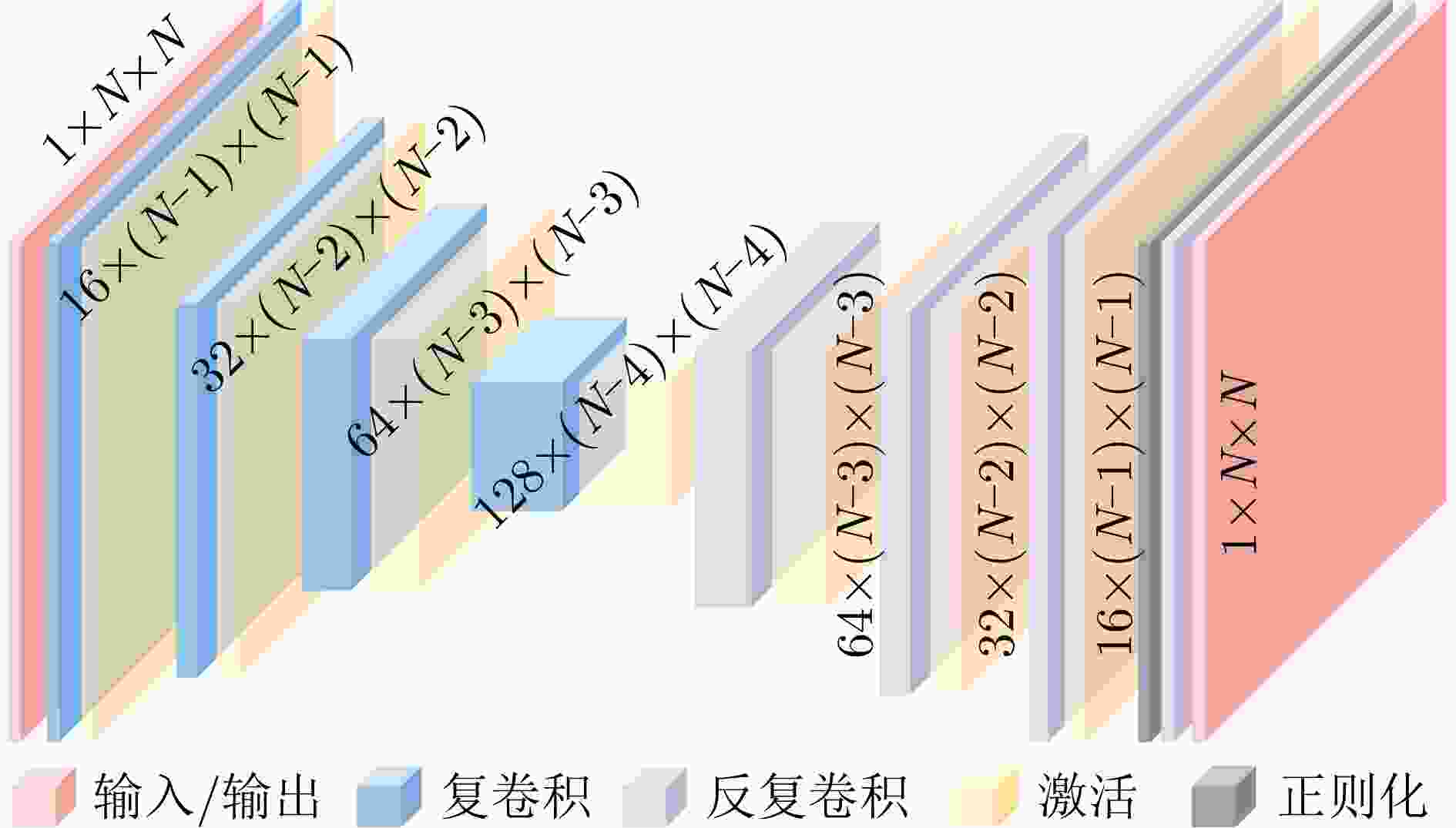
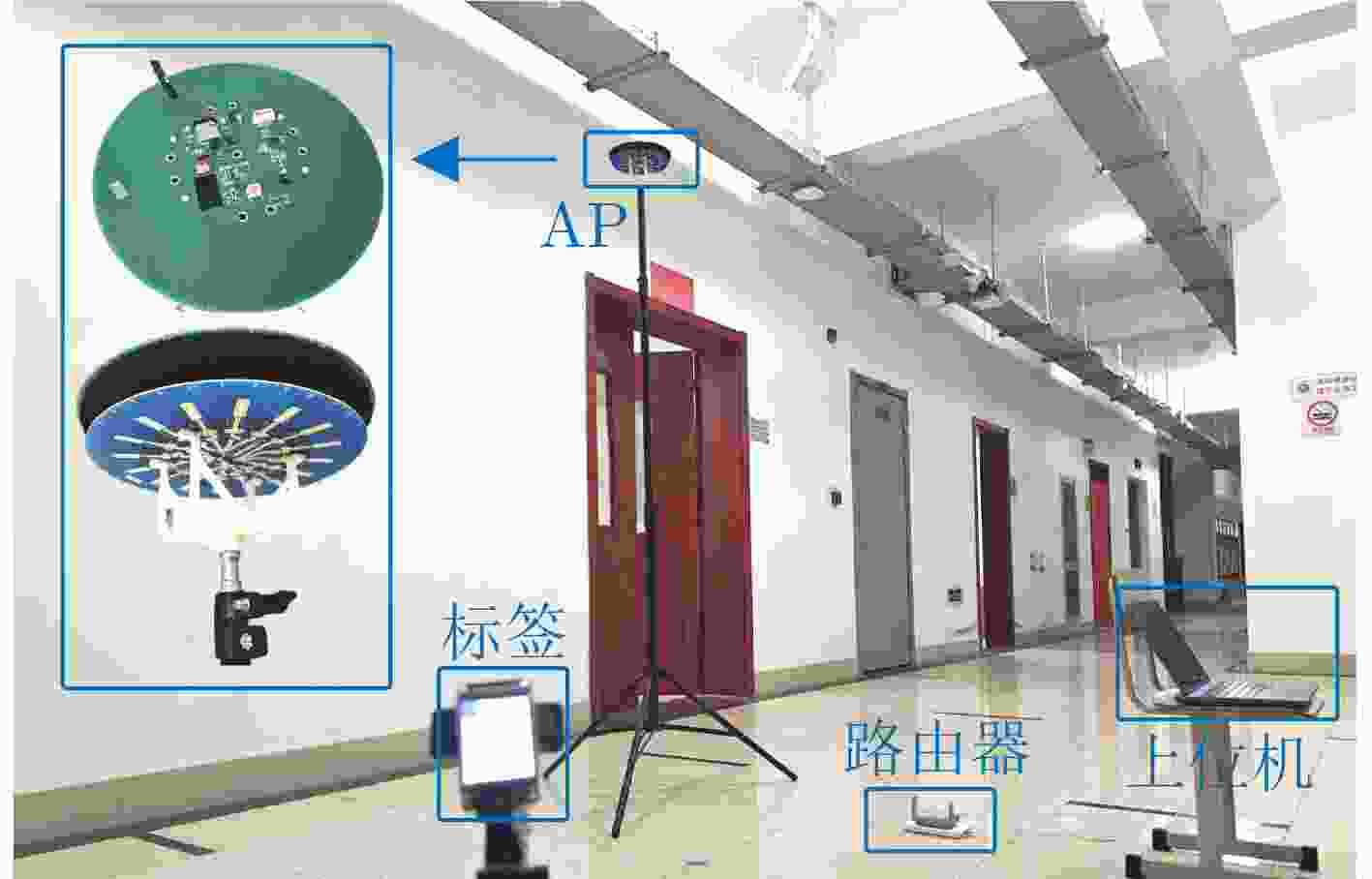
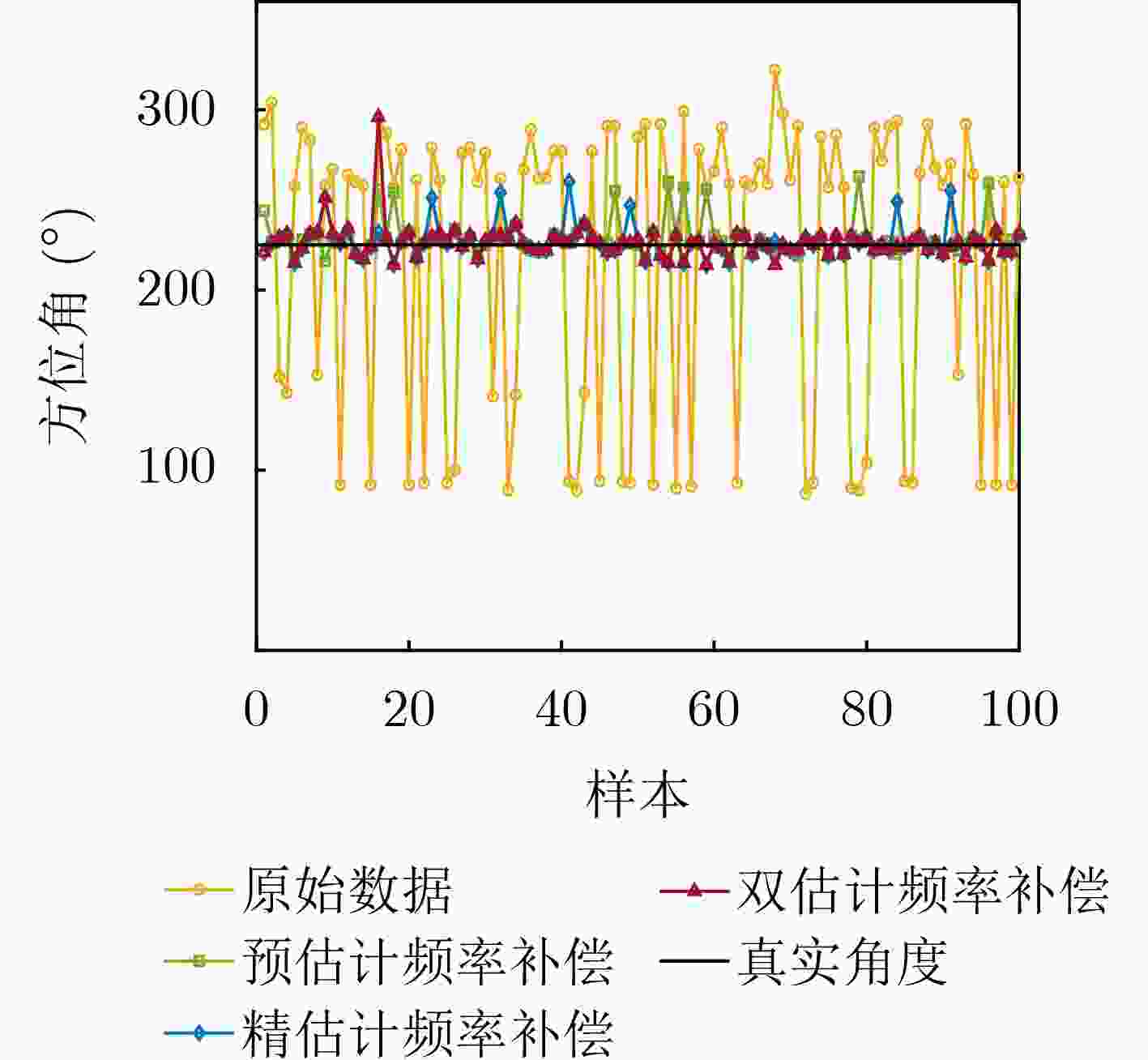
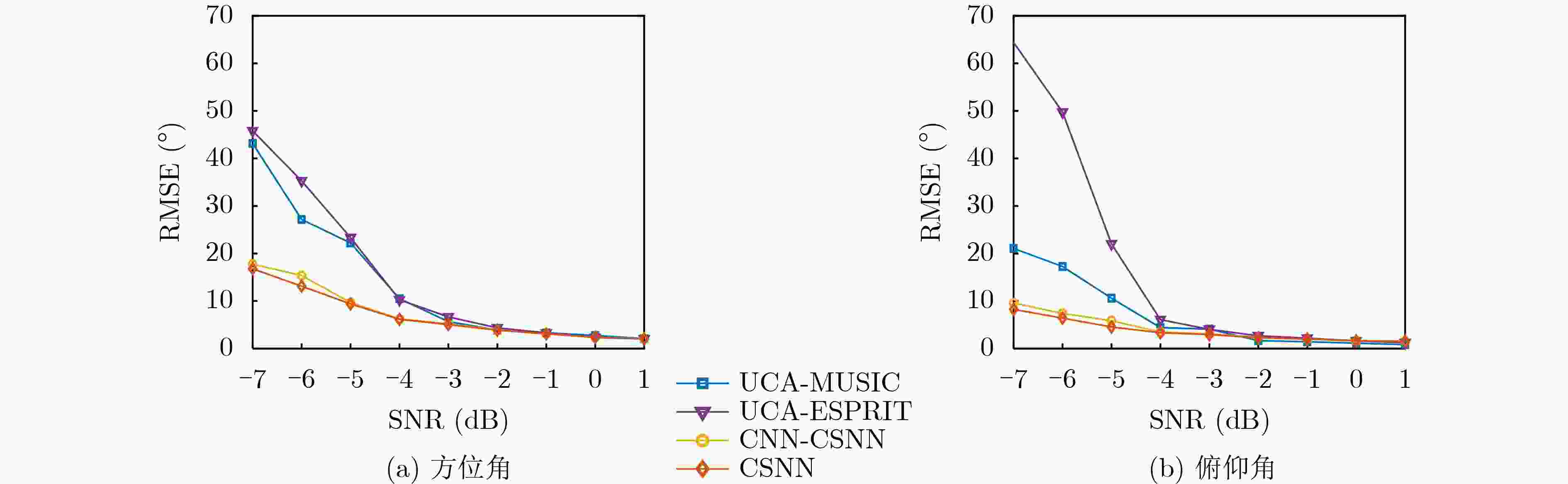
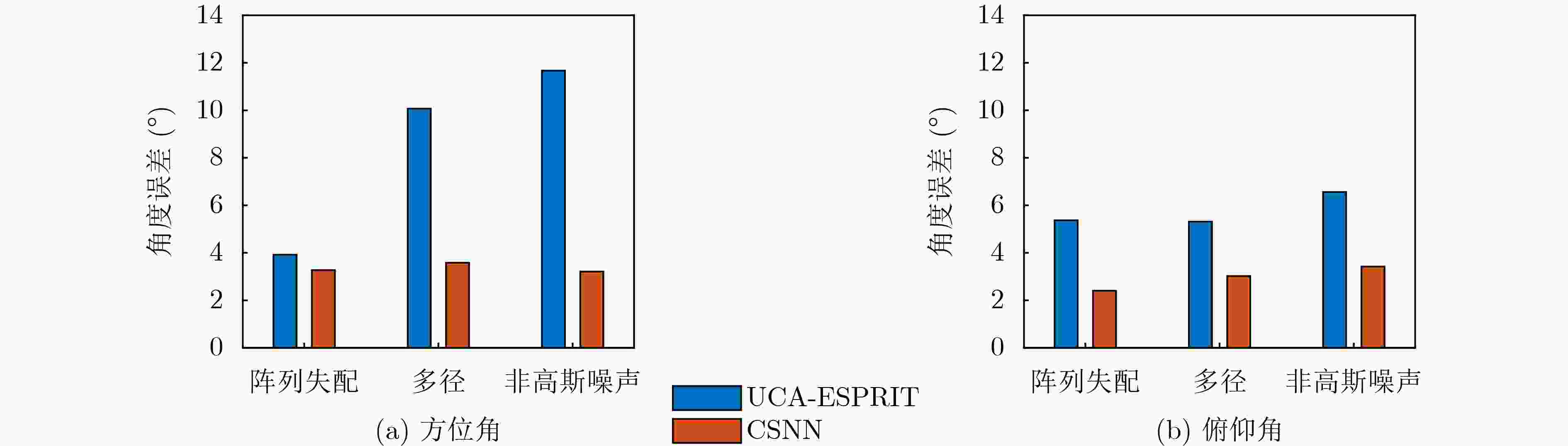
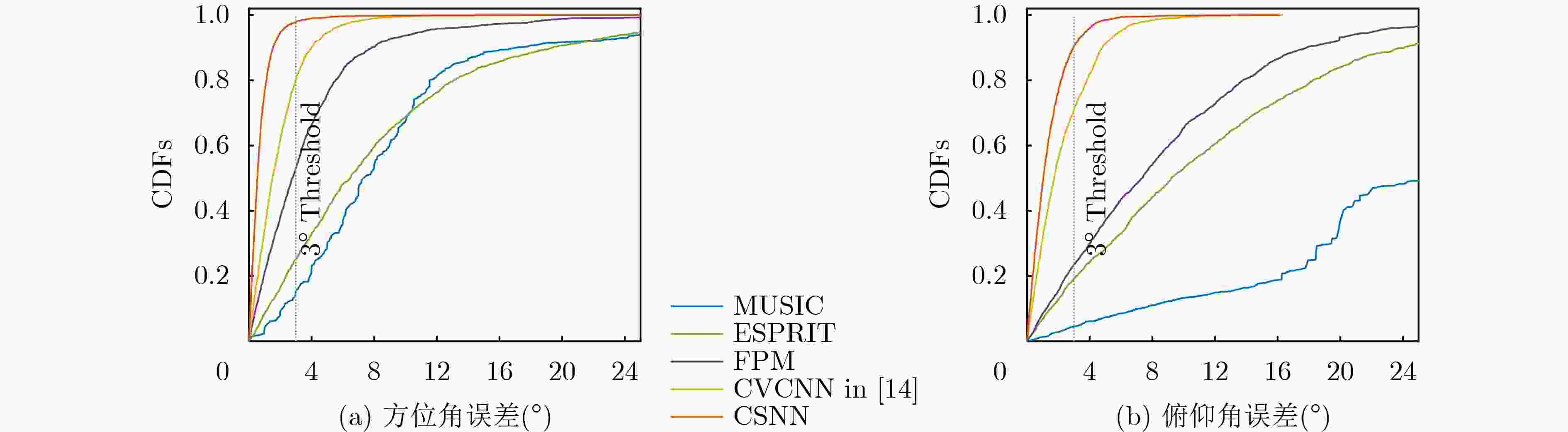
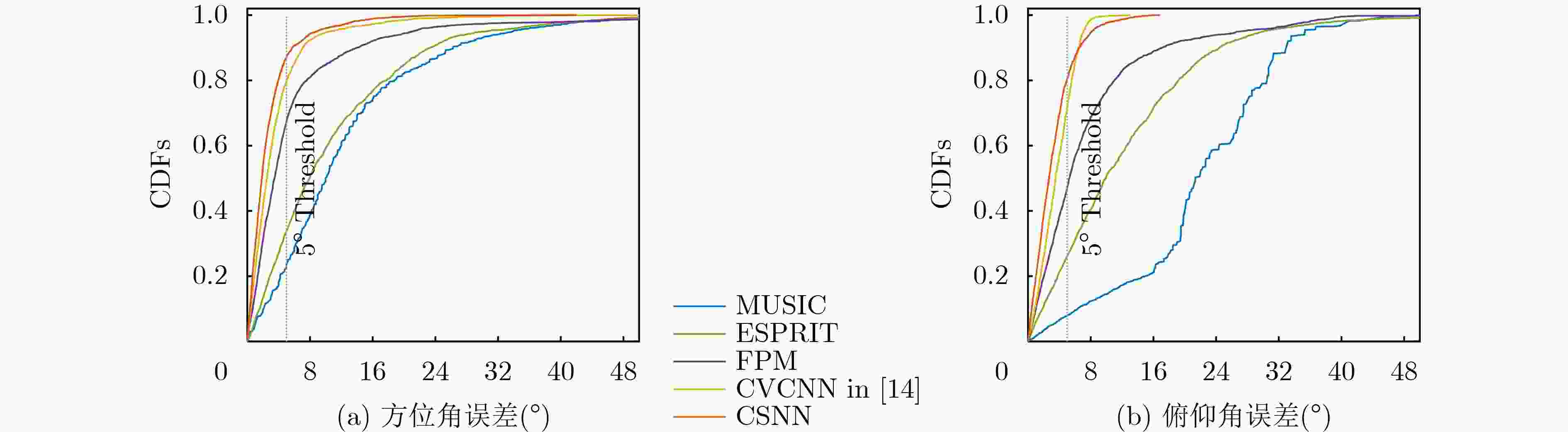
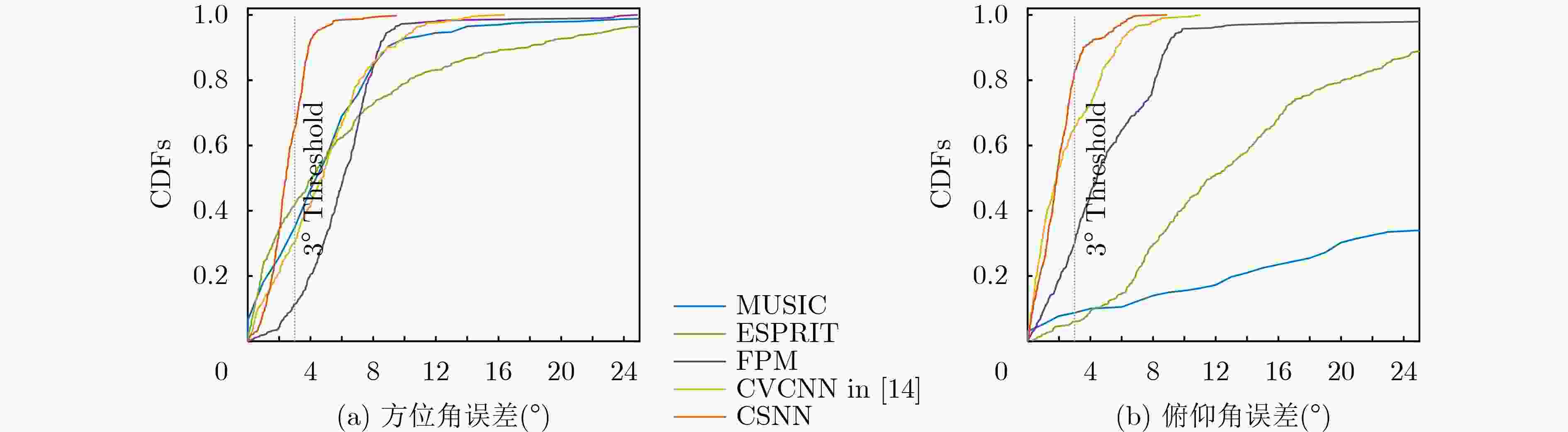
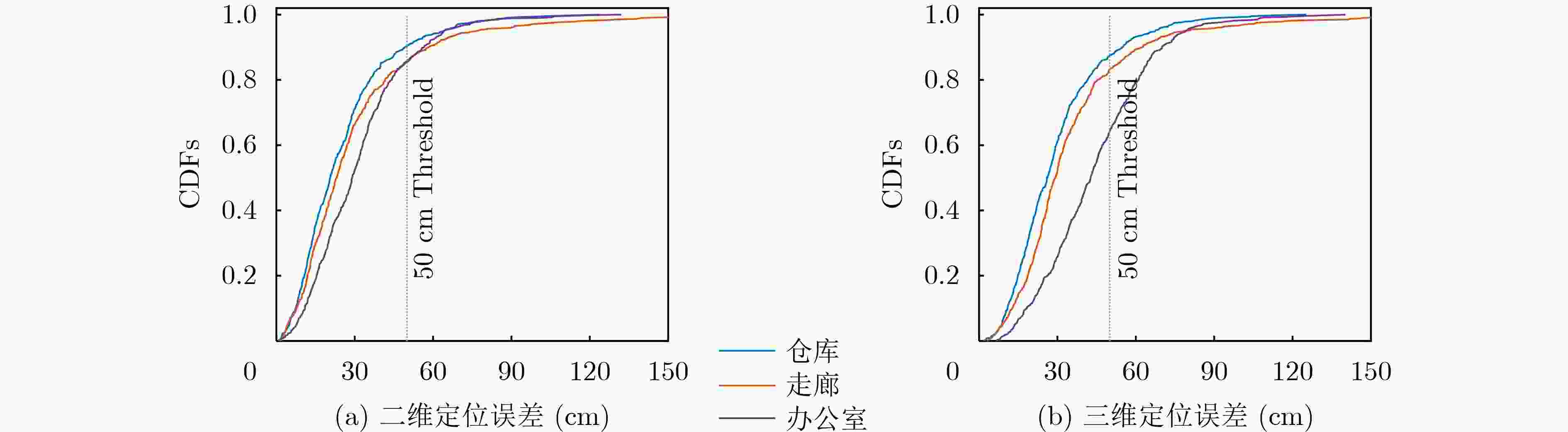
Objective High-precision indoor localization is increasingly required in intelligent service scenarios, yet existing techniques continue to face difficulties in complex environments where signal frequency offset, multipath propagation, and noise interfere with accuracy. To address these limitations, a 3D localization method using a Uniform Circular Array (UCA) driven by a Complex Subspace Neural Network (CSNN) is proposed to improve accuracy and robustness under challenging conditions. Methods The proposed method establishes a complete localization pipeline based on a hierarchical signal processing framework that includes frequency offset compensation, two-dimensional angle estimation, and spatial mapping ( Fig. 2 ). A dual-estimation frequency compensation algorithm is first designed. The frequency offsets during the Channel Time Extension (CTE) reference period and sample period are estimated separately, and the estimate obtained from the reference period is used to resolve ambiguity in the antenna sample period, which enables high-precision frequency compensation. The CSNN is then constructed to estimate the two-dimensional angle (Fig. 3 ). Within this framework, a Complex-Valued Convolutional Neural Network (CVCNN) (Fig. 4 ) is introduced to calibrate the covariance matrix of the received signals, which suppresses correlated noise and multipath interference. Based on the theory of mode-space transformation, the calibrated covariance matrix is projected onto a virtual Uniform Linear Array (ULA). The azimuth and elevation angles are jointly estimated by the ESPRIT algorithm. The estimated angles from three Access Points (APs) are subsequently fused to obtain the final position estimate.Results and Discussions Experiments are conducted to evaluate the performance of the proposed method. For frequency offset suppression, the dual-estimation frequency compensation algorithm markedly reduces the effect on angle estimation, improving estimation accuracy by 91.7% compared with uncorrected data and showing clear improvement over commonly used approaches ( Fig. 6 ). For angle estimation, the CSNN achieves reductions of more than 40% in azimuth error and 25% in elevation error compared with the MUSIC algorithm under simulation conditions (Fig. 7 ), and verifies the capability of the CVCNN module to suppress various interferences. In practical experiments, the CSNN achieves an average azimuth error of 1.07° and an average elevation error of 1.28° in the training scenario (Table 1 ,Fig. 10 ). Generalization experiments conducted in three indoor environments (warehouse, corridor, and office) show that the average angular errors remain low at 2.78° for azimuth and 3.39° for elevation (Table 2 ,Fig. 11 ). The proposed method further maintains average positioning accuracies of 28.9 cm in 2D and 36.5 cm in 3D after cross-scene migration (Table 4 ,Fig. 13 ).Conclusions The proposed high-precision indoor localization method integrates dual-estimation frequency compensation, the CSNN angle estimation algorithm, and three-AP cooperative localization. It demonstrates strong performance in both simulation and real-environment experiments. The method also maintains stable cross-scene adaptability and accuracy that meet the requirements of high-precision indoor localization. -
表 1 大厅场景角度估计误差(°)
方法 方位角 俯仰角 UCA-ESPRIT 9.23 11.48 UCA-MUSIC 10.48 22.84 FPM 5.94 9.85 CVCNN[14] 1.97 2.21 CSNN 1.07 1.28 表 2 跨场景角度估计误差(°)
方法 仓库 走廊 办公室 平均 UCA-ESPRIT [8.01, 10.15] [9.91, 12.03] [11.37, 14.28] [9.76, 12.15] UCA-MUSIC [8.78, 22.46] [10.49, 20.90] [13.59, 23.28] [10.90, 22.21] FPM [3.75, 9.70] [3.89, 7.81] [8.09, 10.39] [5.24, 9.30] CVCNN[14] [3.46, 3.27] [3.49, 3.31] [3.75, 4.21] [3.57, 3.60] CSNN [2.23, 2.73] [2.78, 3.11] [3.33, 4.32] [2.78, 3.39] 注:[a, b]表示a为方位角误差,b为俯仰角误差。 表 3 单信源与多信源角度估计误差(°)
方法 单信源 多信源 UCA-ESPRIT [7.29, 10.06] [6.45, 13.97] UCA-MUSIC [4.81, 25.59] [5.21, 26.84] FPM [5.39, 4.83] [6.12, 5.58] CVCNN[14] [3,53, 2.80] [4.94, 2.54] CSNN [2.95, 1.61] [2.81, 2.15] 注:[a, b]表示a为方位角误差,b为俯仰角误差。 表 4 4类场景下二维和三维定位平均误差(cm)
方法 仓库 走廊 办公室 大厅 UCA-ESPRIT [89.7, 128.5] [118.1, 144.6] [122.2, 174.2] [109.4, 138.2] UCA-MUSIC [102.9, 167.0] [114.6, 171.7] [147.5, 196.9] [111.2, 166.1] FPM [39.6, 72.4] [36.8, 64.5] [79.2, 118.1] [58.5, 79.2] CVCNN[14] [33.2, 36.2] [30.7, 38.5] [38.8, 46.0] [21.8, 27.7] CSNN [25.1, 29.7] [30.1, 35.5] [31.5, 44.3] [18.1, 24.6] 注:[a, b]表示a为二维定位误差,b为三维定位误差。 -
[1] 杨秀建, 皇甫尚昆, 敖鹏, 等. 基于改进全质心-Taylor的UWB定位方法[J]. 仪器仪表学报, 2024, 45(10): 284–294. doi: 10.19650/j.cnki.cjsi.J2412618.YANG Xiujian, HUANGPU Shangkun, AO Peng, et al. Improved full-centroid-Taylor based UWB localization[J]. Chinese Journal of Scientific Instrument, 2024, 45(10): 284–294. doi: 10.19650/j.cnki.cjsi.J2412618. [2] 赵万龙, 田新元, 陈超, 等. 联合Spline插值的Wi-Fi指纹匹配定位算法[J]. 电子与信息学报, 2024, 46(9): 3563–3570. doi: 10.11999/JEIT230116.ZHAO Wanlong, TIAN Xinyuan, CHEN Chao, et al. Wi-Fi fingerprint localization uniting spline interpolation[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3563–3570. doi: 10.11999/JEIT230116. [3] ZHUANG Yuan, ZHANG Chongyang, HUAI Jianzhu, et al. Bluetooth localization technology: Principles, applications, and future trends[J]. IEEE Internet of Things Journal, 2022, 9(23): 23506–23524. doi: 10.1109/JIOT.2022.3203414. [4] SAMBU P and WON M. An experimental study on direction finding of Bluetooth 5.1: Indoor vs outdoor[C]. 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, USA, 2022: 1934–1939. doi: 10.1109/WCNC51071.2022.9771930. [5] PAULINO N and PESSOA L M. Self-localization via circular Bluetooth 5.1 antenna array receiver[J]. IEEE Access, 2023, 11: 365–395. doi: 10.1109/ACCESS.2022.3233130. [6] HUANG Chenglin, TIAN Zengshan, HE Wei, et al. Spotlight: A 3-D indoor localization system in wireless sensor networks based on orientation and RSSI measurements[J]. IEEE Sensors Journal, 2023, 23(21): 26662–26676. doi: 10.1109/JSEN.2023.3315790. [7] YE Hongyun, YANG Biao, LONG Zhiqiang, et al. A method of indoor positioning by signal fitting and PDDA algorithm using BLE AOA device[J]. IEEE Sensors Journal, 2022, 22(8): 7877–7887. doi: 10.1109/JSEN.2022.3141739. [8] WANG Bowen, WANG Yunlong, QIU Xinyou, et al. BLE localization with polarization sensitive array[J]. IEEE Wireless Communications Letters, 2021, 10(5): 1014–1017. doi: 10.1109/LWC.2021.3055558. [9] KHAN A, WANG S, and ZHU Ziming. Angle-of-arrival estimation using an adaptive machine learning framework[J]. IEEE Communications Letters, 2019, 23(2): 294–297. doi: 10.1109/LCOMM.2018.2884464. [10] PHILIPS D R, SALAMI E, RAMIAH H, et al. Location accuracy optimization in Bluetooth Low Energy (BLE) 5.1-based Indoor Positioning System (IPS)—a machine learning approach[J]. IEEE Access, 2023, 11: 140186–140201. doi: 10.1109/ACCESS.2023.3338358. [11] MATHEWS C P and ZOLTOWSKI M D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays[J]. IEEE Transactions on Signal Processing, 1994, 42(9): 2395–2407. doi: 10.1109/78.317861. [12] MCKILLIAM R G, QUINN B G, CLARKSON I V L, et al. Frequency estimation by phase unwrapping[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 2953–2963. doi: 10.1109/TSP.2010.2045786. [13] CHEN Peng, CHEN Zhimin, LIU Liang, et al. SDOA-Net: An efficient deep-learning-based DOA estimation network for imperfect array[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 8503512. doi: 10.1109/TIM.2024.3391338. [14] HU Shulin, ZENG Cao, LIU Minti, et al. Robust DOA estimation using deep complex-valued convolutional networks with sparse prior[C]. 2023 6th International Conference on Information Communication and Signal Processing (ICICSP), Xi'an, China, 2023: 234–239. doi: 10.1109/ICICSP59554.2023.10390873. [15] XU Xiaoxuan and HUANG Qinghua. MD-DOA: A model-based deep learning DOA estimation architecture[J]. IEEE Sensors Journal, 2024, 24(12): 20240–20253. doi: 10.1109/JSEN.2024.3396337. [16] SHMUEL D H, MERKOFER J P, REVACH G, et al. SubspaceNet: Deep learning-aided subspace methods for DoA estimation[J]. IEEE Transactions on Vehicular Technology, 2025, 74(3): 4962–4976. doi: 10.1109/TVT.2024.3496119. -





 下载:
下载:




 下载:
下载:
