铁电基的存算一体组合优化求解器

钱煜; 杨泽禹; 王然然; 蔡嘉豪; 李超; 黄庆荣; 樊凌雁; 李云龙; 卓成; 尹勋钊

doi:10.11999/JEIT250369

铁电基的存算一体组合优化求解器

doi: 10.11999/JEIT250369 cstr: 32379.14.JEIT250369

钱煜¹,
杨泽禹¹,
王然然³,
蔡嘉豪¹,
李超¹,
黄庆荣¹,
樊凌雁²,
李云龙³,
卓成^{3, 4},
尹勋钊^{1, 4, ,}

1.
浙江大学信息与电子工程学院杭州 310058
2.
杭州电子科技大学微电子研究院杭州 310018
3.
浙江大学集成电路学院杭州 310058
4.
浙江省协同传感与自主无人系统重点实验室杭州 310058

基金项目: 长三角科技创新共同体联合攻关项目(2024CSJZN0500)，国家自然科学基金(624B2126, W2412034, 92164203)，中德联合基金(M-0612)

详细信息

作者简介:
钱煜：男，博士生，研究方向为存算一体跨层次设计优化、组合优化求解器

杨泽禹：男，博士生，研究方向为面向神经网络加速的存算一体电路设计优化

王然然：女，博士生，研究方向为存算一体器件电路设计优化

蔡嘉豪：男，博士生，研究方向为存算一体电路架构设计优化

李超：男，博士生，研究方向为存算一体电路算法协同设计优化

黄庆荣：男，博士生，研究方向为存算一体电路架构设计优化

樊凌雁：女，研究员，研究方向为数据存储、高速接口集成电路设计

李云龙：男，教授，研究方向为先进CMOS芯片工艺与可靠性、芯片异构集成(芯粒)工艺与可靠性、硅基特殊成像器件工艺集成

卓成：男，教授，研究方向为设计自动化、低功耗芯片设计、人工智能算法及硬件

尹勋钊：男，研究员，研究方向为人工智能、存算一体、新型计算专用芯片设计、软硬件跨层协同设计优化、组合优化求解器

通讯作者:
尹勋钊　xzyin1@zju.edu.cn

中图分类号: TP333.5
计量
- 文章访问数: 127
- HTML全文浏览量: 68
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2025-05-06
- 修回日期: 2025-08-28
- 网络出版日期: 2025-09-02

Ferroelectric FET-based Compute-in-Memory Solver for Combinatorial Optimization Problems

1.
College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou 310058, China
2.
Microelectronics Research Institute, Hangzhou Dianzi University, Hangzhou 310018, China
3.
College of Integrated Circuits, Zhejiang University, Hangzhou 310058, China
4.
Key Laboratory of Collaborative Sensing and Autonomous Unmanned Systems of Zhejiang Province, Hangzhou 310058, China

Funds: Yangtze River Delta Science and Technology Innovation Community Joint Fundamental Research Project (2024CSJZN0500), The National Natural Science Foundation of China (624B2126, W2412034, 92164203), SGC Cooperation Project (M-0612)

摘要

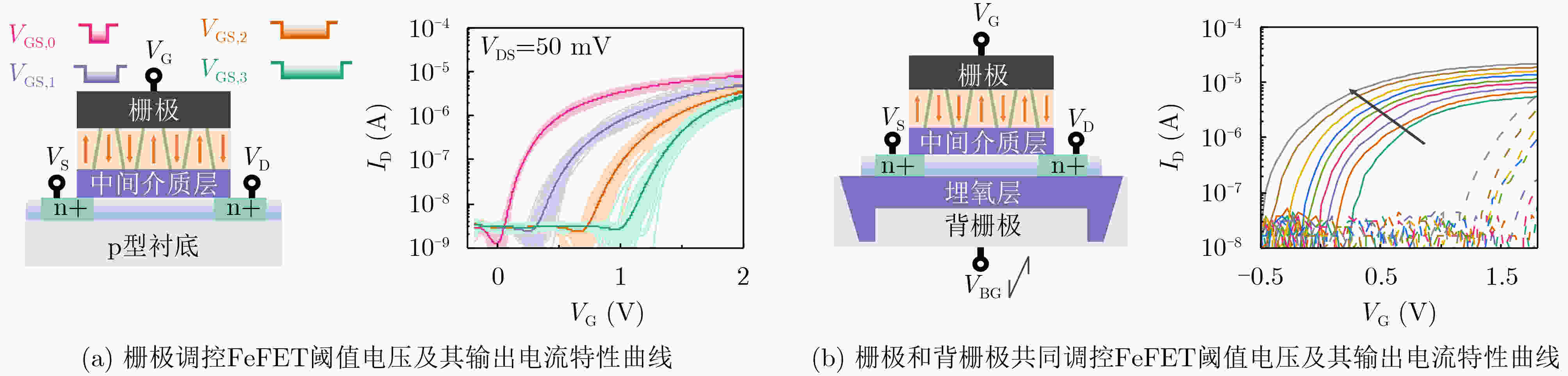
摘要: 组合优化问题在诸多领域应用广泛，大多属于非确定多项式时间难题，基于冯·诺依曼架构的传统数字计算机难以满足其极高计算复杂度的需求。具有阈值电压可编程特性和多端口输入结构的铁电晶体管(FeFET)为高效求解组合优化问题提供了新的机遇。基于FeFET的存算一体架构具有能效高、延时低等特点，同时支持对向量-矩阵及向量-矩阵-向量乘法等复杂算子的加速，非常适合求解组合优化问题。该文回顾了FeFET的器件特性，介绍了组合优化问题的基本求解过程，并进一步探讨了近年来面向等式约束、不等式约束和纳什均衡场景下基于FeFET的存算一体组合优化求解器工作。最后，该文从多个方面分析并展望了基于FeFET的存算一体组合优化求解器的前景与挑战。
- 铁电晶体管 /
- 存算一体 /
- 组合优化
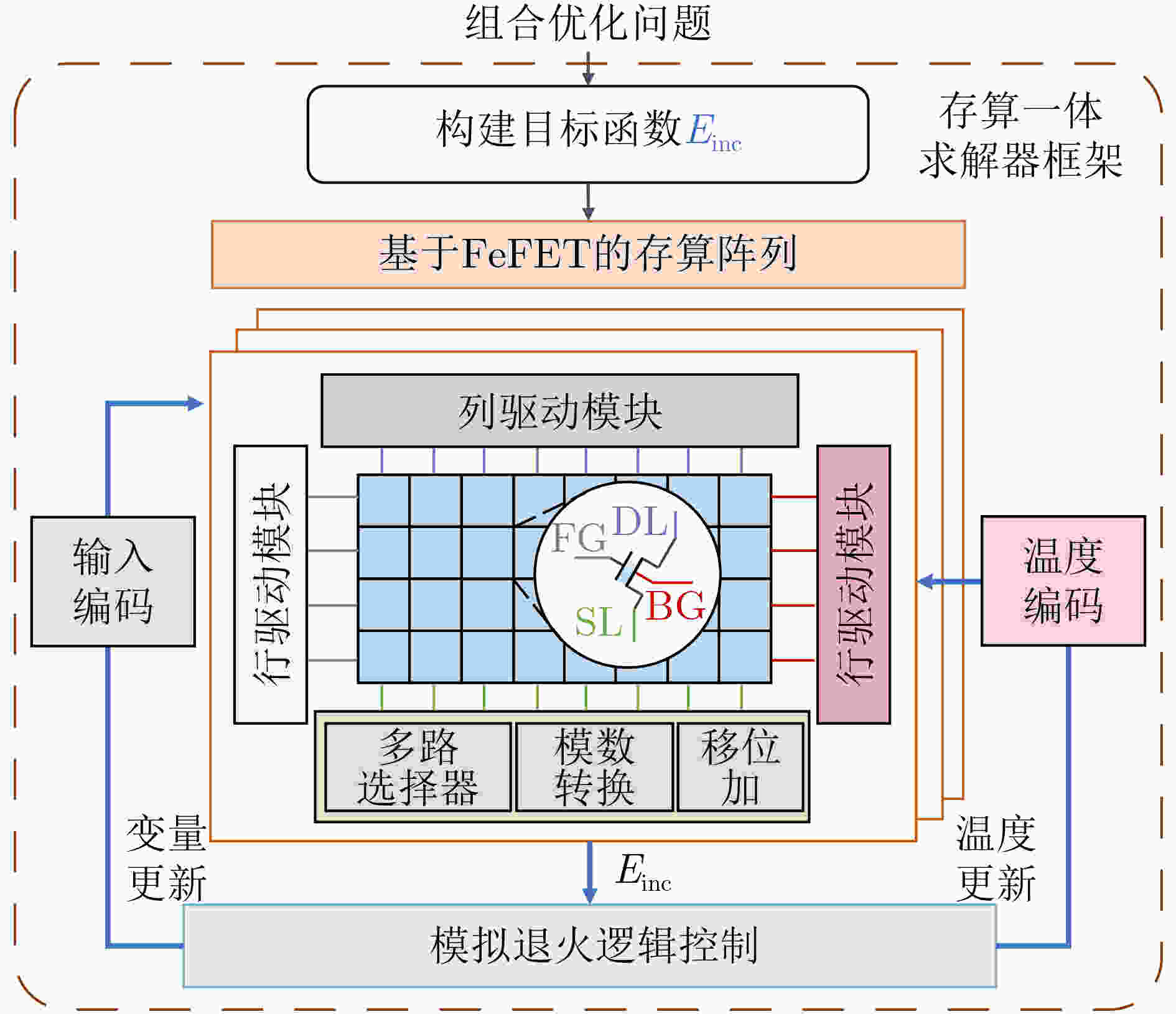
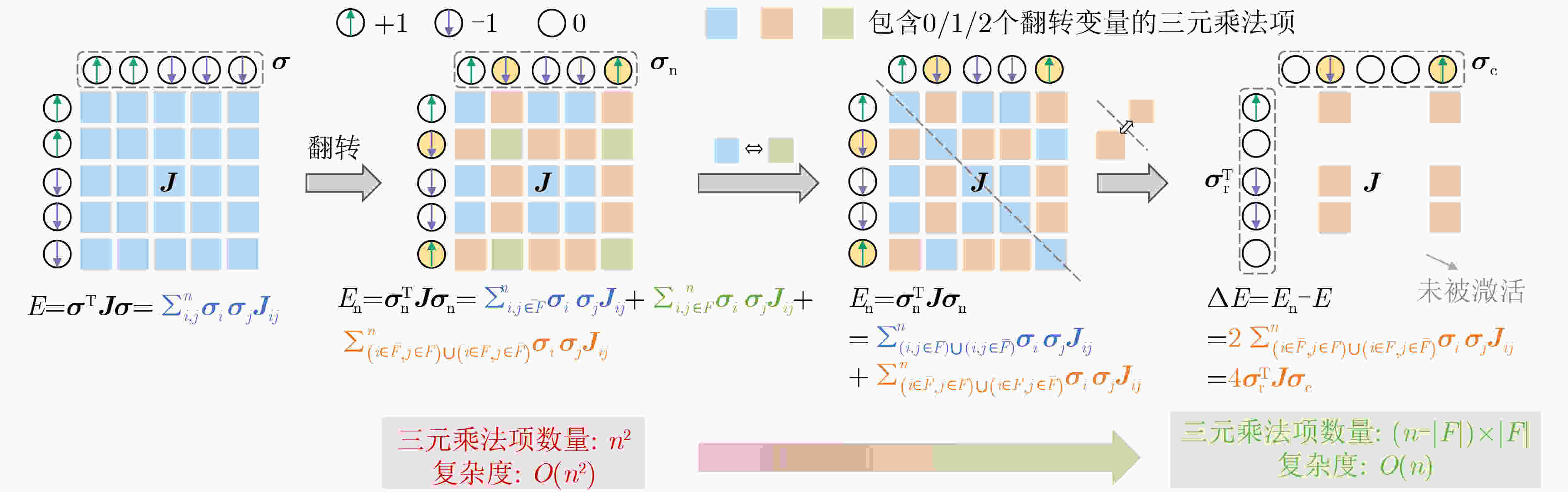
Abstract: Significance Combinatorial optimization problems (COPs) are ubiquitous, profoundly impacting diverse fields from logistics and finance to advanced AI and drug discovery. At their core, these problems demand identifying the absolute best solution from an often unfathomably vast set of possibilities. The vast majority of COPs are classified as NP-hard problems, representing one of the most significant computational challenges in computer science. Traditional digital computers, operating on the von Neumann architecture, face immense difficulties in solving COPs; as problem scales expand, required computational resources, particularly latency, increase exponentially. Given these limitations, there's an urgent need to explore novel architectures for efficiently solving COPs, a pursuit with both significant theoretical importance and profound practical implications for tackling complex, resource-intensive real-world problems. Addressing these challenges, researchers have actively explored various novel hardware-based combinatorial optimization solutions, often transforming COPs into Ising models or Quadratic Unconstrained Binary Optimization (QUBO) problems for hardware implementation. Broadly, existing approaches fall into two categories: digital Application-Specific Integrated Circuit (ASIC) annealers, which suffer from data movement bottlenecks, and dynamical system solvers, which leverage physical dynamics but often demand high device parameter precision, struggle with cross-chip scalability, and may find it difficult to integrate Ising model self-interaction terms. Beyond these, other non-traditional methods like quantum computing (e.g., D-Wave's quantum annealers requiring cryogenic cooling and having limited connectivity) and certain optical computing approaches (e.g., relying on extremely long optical fibers) exist. While offering unique physical advantages, they generally face substantial challenges in integrating with mature silicon-based Very Large Scale Integration (VLSI) circuits. Consequently, despite a range of novel hardware solutions, their individual limitations highlight the critical need for new combinatorial optimization solvers that offer higher integration, better scalability, superior energy efficiency, and broader problem type support. Process Ferroelectric field-effect transistors (FeFETs), with their unique threshold voltage programmability and multi-port input structure, are opening exciting new avenues for efficiently solving combinatorial optimization problems (COPs). The FeFET-based compute-in-memory (CiM) architecture is particularly well-suited for these challenges, boasting high energy efficiency, low latency, and the inherent ability to accelerate complex operations like vector-matrix and vector-matrix-vector multiplications. Recent research has seen numerous works proposing FeFET-based CiM COP solvers to tackle a diverse range of problems, including those with equality constraints, inequality constraints, and Nash equilibrium scenarios. The overall solving process for these innovative FeFET-based CiM solutions generally involves four key steps: (1) Problem transformation, where the COP is converted into a hardware-friendly objective function, often by encoding equality constraints, introducing slack variables or penalty methods for inequality constraints, or formulating coupled optimization problems for Nash equilibrium scenarios; (2) Following transformation, the objective function undergoes a crucial compression process. This is specifically achieved by analyzing the simulated annealing algorithm itself, which allows for the partial activation of matrix columns, thus significantly reducing the typical computational complexity associated with fully active matrices. Furthermore, this step involves approximating and merging the exponential function components inherent in the algorithm directly into the matrix representation, thereby optimizing the function for efficient hardware implementation on the CiM array; (3) Leveraging the unique three-port and four-port structures of FeFETs, specialized CiM circuit designs are utilized to achieve high-speed acceleration of the compressed objective function. This allows for the efficient computation of a single iteration or a key part of the objective function often within a single clock cycle, significantly mitigating the von Neumann bottleneck; and (4) Finally, based on the optimized and simplified objective function, combinatorial optimization algorithms, such as simulated annealing, are simplified and applied over multiple cycles. This iterative process, efficiently accelerated by the underlying CiM hardware, aims to achieve high-quality and efficient solutions for the given problem. This structured approach highlights the adaptability and potential of FeFET-based CiM for a broad spectrum of challenging combinatorial optimization tasks. Conclusions This paper provides a comprehensive review of FeFET-based CiM solvers for solving COPs, which are prevalent across various domains and demand significant computational resources. It first outlines the device characteristics of FeFET and the fundamental process of solving COPs. The core of the paper focused on recent advancements in FeFET-based CiM solvers tailored for three specific scenarios: equality constraints, inequality constraints, and Nash equilibrium. The discussion highlighted how these architectures leverage the unique properties of FeFET to address the computational intensity of these problems. Prospects FeFET-based COP solvers show immense potential. By merging FeFET device strengths with CiM advantages, these solvers offer an efficient path to tackling highly complex optimization challenges, leading to substantial gains in speed and energy efficiency for real-world problems. However, significant challenges remain: (1) FeFET endurance is limited, restricting the number of processable problems. (2) Analog-to-digital converters (ADCs) in FeFET CiM arrays incur large area, power, and latency overheads. (3) Simulated annealing algorithms, when applied to large-scale problems, suffer from slow convergence due to increased iterations. Addressing these will be crucial for the widespread adoption and advancement of FeFET-based CiM solutions.
- Ferroelectric FET (FeFET) /
- Compute-in-Memory (CiM) /
- Combinatorial optimization

HTML全文

图 1 FeFET器件的阈值电压可编程特性^[37,41]

下载: 全尺寸图片幻灯片

图 2 FeFET器件的多端口输入特性

下载: 全尺寸图片幻灯片

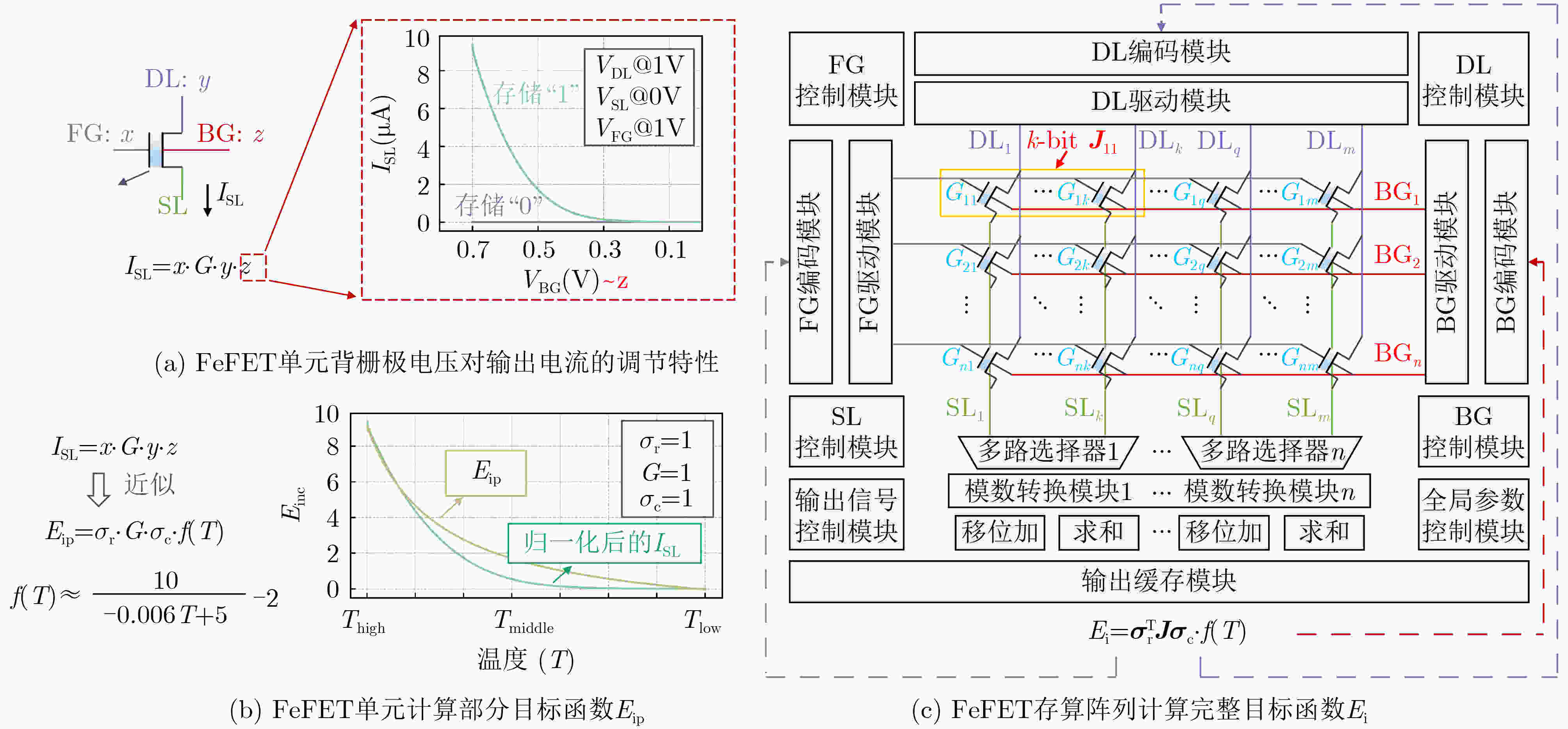
图 3 面向等式约束的存算一体组合优化求解器^[40]

下载: 全尺寸图片幻灯片

图 4 目标函数的去冗余算法

下载: 全尺寸图片幻灯片

图 5 基于FeFET的存算阵列实现目标函数计算

下载: 全尺寸图片幻灯片

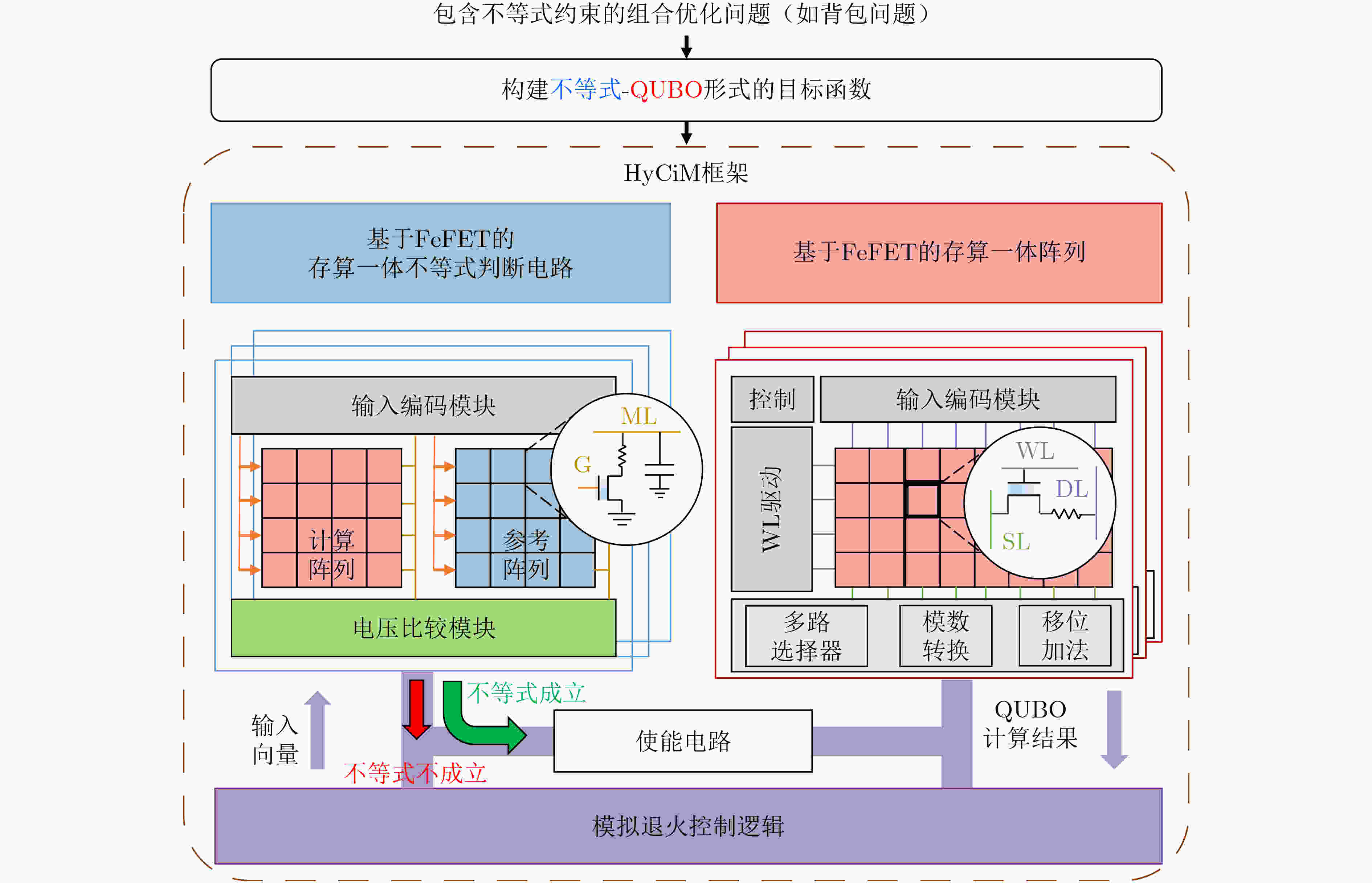
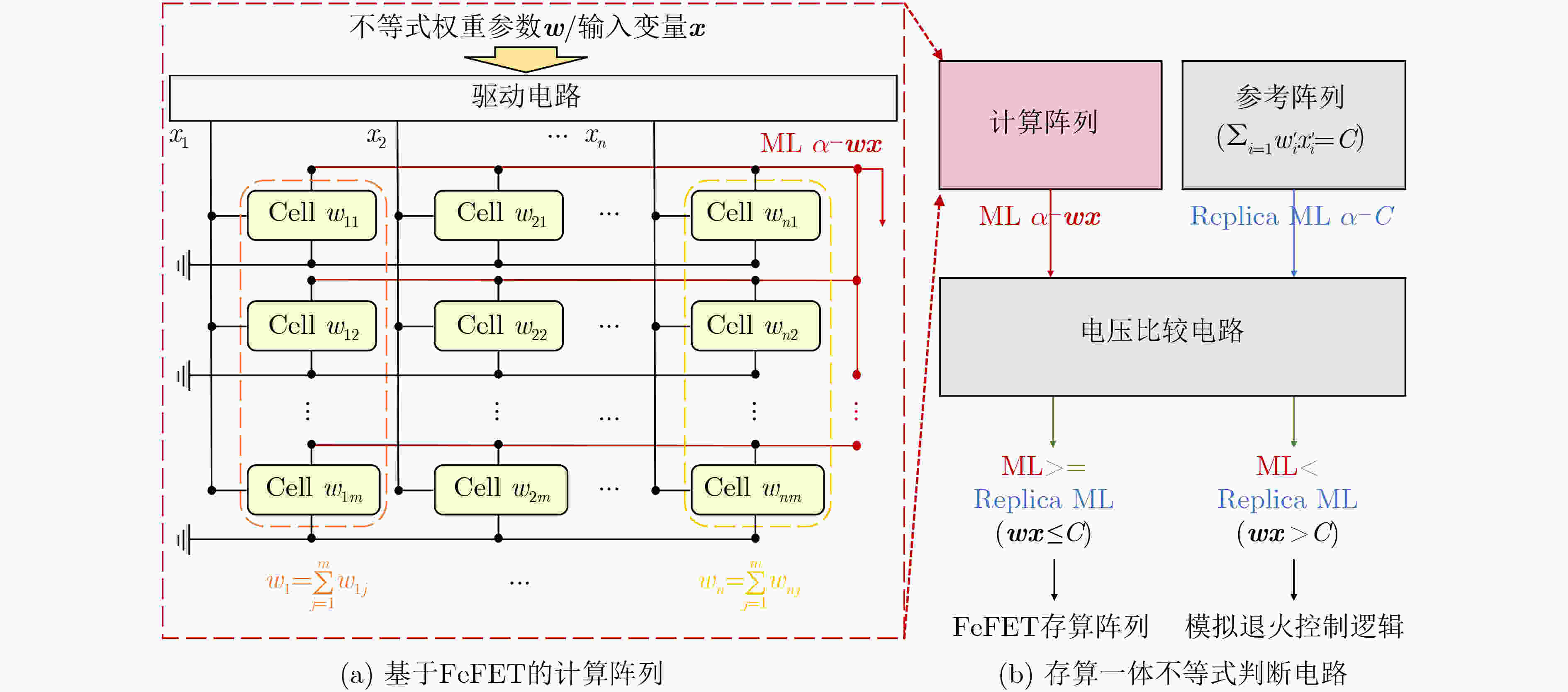
图 6 面向不等式约束的存算一体组合优化求解器HyCiM^[37]

下载: 全尺寸图片幻灯片

图 7 HyCiM求解器中的存算一体不等式判断电路

下载: 全尺寸图片幻灯片

图 8 面向纳什均衡的存算一体组合优化求解器C-Nash^[38,39]

下载: 全尺寸图片幻灯片

图 9 支持小数输入的存算阵列

下载: 全尺寸图片幻灯片

参考文献(61)

[1]	Industrial Applications of Combinatorial Optimization[M]. Springer Science & Business Media, 2013.
[2]	ROBERTS F S and TESMAN B. Applied Combinatorics[M]. 3rd ed. Boca Raton: CRC Press, 2024.
[3]	NASERI G and KOFFAS M A G. Application of combinatorial optimization strategies in synthetic biology[J]. Nature Communications, 2020, 11(1): 2446. doi: 10.1038/s41467-020-16175-y.
[4]	BARAHONA F, GRÖTSCHEL M, JÜNGER M, et al. An application of combinatorial optimization to statistical physics and circuit layout design[J]. Operations Research, 1988, 36(3): 493–513. doi: 10.1287/opre.36.3.493.
[5]	MARKOV I L. Limits on fundamental limits to computation[J]. Nature, 2014, 512(7513): 147–154. doi: 10.1038/nature13570.
[6]	ZHU Shiqiang, YU Ting, XU Tao, et al. Intelligent computing: The latest advances, challenges, and future[J]. Intelligent Computing, 2023, 2: 0006. doi: 10.34133/icomputing.0006.
[7]	GREENLAW R, HOOVER H J, and RUZZO W L. Limits to Parallel Computation: P-Completeness Theory[M]. New York: Oxford University Press, 1995.
[8]	LUCAS A. Ising formulations of many NP problems[J]. Frontiers in Physics, 2014, 2: 5. doi: 10.3389/fphy.2014.00005.
[9]	MOHSENI N, MCMAHON P L, and BYRNES T. Ising machines as hardware solvers of combinatorial optimization problems[J]. Nature Reviews Physics, 2022, 4(6): 363–379. doi: 10.1038/s42254-022-00440-8.
[10]	DATE P, ARTHUR D, and PUSEY-NAZZARO L. QUBO formulations for training machine learning models[J]. Scientific Reports, 2021, 11(1): 10029. doi: 10.1038/s41598-021-89461-4.
[11]	YAMAMOTO K, KAWAMURA K, ANDO K, et al. STATICA: A 512-spin 0.25 M-weight annealing processor with an all-spin-updates-at-once architecture for combinatorial optimization with complete spin–spin interactions[J]. IEEE Journal of Solid-State Circuits, 2021, 56(1): 165–178. doi: 10.1109/JSSC.2020.3027702.
[12]	KATSUKI K, SHIN D, ONIZAWA N, et al. Fast solving complete 2000-node optimization using stochastic-computing simulated annealing[C]. Proceedings of the 29th IEEE International Conference on Electronics, Circuits and Systems, Glasgow, United Kingdom, 2022: 1–4. doi: 10.1109/ICECS202256217.2022.9971124.
[13]	ONIZAWA N, KUROKI K, SHIN D, et al. Local energy distribution based hyperparameter determination for stochastic simulated annealing[J]. IEEE Open Journal of Signal Processing, 2023, 4: 452–461. doi: 10.1109/OJSP.2023.3329756.
[14]	TAKEMOTO T, YAMAMOTO K, YOSHIMURA C, et al. 4.6 A 144Kb annealing system composed of 9×16Kb annealing processor chips with scalable chip-to-chip connections for large-scale combinatorial optimization problems[C]. Proceedings of 2021 IEEE International Solid-State Circuits Conference, San Francisco, USA, 2021: 64–66. doi: 10.1109/ISSCC42613.2021.9365748.
[15]	MOY W, AHMED I, CHIU P W, et al. A 1, 968-node coupled ring oscillator circuit for combinatorial optimization problem solving[J]. Nature Electronics, 2022, 5(5): 310–317. doi: 10.1038/s41928-022-00749-3.
[16]	AHMED I, CHIU P W, MOY W, et al. A probabilistic compute fabric based on coupled ring oscillators for solving combinatorial optimization problems[J]. IEEE Journal of Solid-State Circuits, 2021, 56(9): 2870–2880. doi: 10.1109/JSSC.2021.3062821.
[17]	DUTTA S, KHANNA A, ASSOA A S, et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators[J]. Nature Electronics, 2021, 4(7): 502–512. doi: 10.1038/s41928-021-00616-7.
[18]	ROYCHOWDHURY J. Bistable latch ising machines[C]. Proceedings of the 19th International Conference on Unconventional Computation and Natural Computation, Espoo, Finland, 2021: 131–148. doi: 10.1007/978-3-030-87993-8_9.
[19]	MALLICK A, ZHAO Zijian, BASHAR M K, et al. CMOS-compatible ising machines built using bistable latches coupled through ferroelectric transistor arrays[J]. Scientific Reports, 2023, 13(1): 1515. doi: 10.1038/s41598-023-28217-8.
[20]	AFOAKWA R, ZHANG Yiqiao, VENGALAM U K R, et al. BRIM: Bistable resistively-coupled ising machine[C]. Proceedings of 2021 IEEE International Symposium on High-Performance Computer Architecture, Seoul, Korea (South), 2021: 749–760. doi: 10.1109/HPCA51647.2021.00068.
[21]	PIERANGELI D, MARCUCCI G, and CONTI C. Large-scale photonic ising machine by spatial light modulation[J]. Physical Review Letters, 2019, 122(21): 213902. doi: 10.1103/PhysRevLett.122.213902.
[22]	HONJO T, SONOBE T, INABA K, et al. 100, 000-spin coherent Ising machine[J]. Science Advances, 2021, 7(40): eabh0952. doi: 10.1126/sciadv.abh0952.
[23]	MCMAHON P L, MARANDI A, HARIBARA Y, et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections[J]. Science, 2016, 354(6312): 614–617. doi: 10.1126/science.aah5178.
[24]	HAMERLY R, INAGAKI T, MCMAHON P L, et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer[J]. Science Advances, 2019, 5(5): eaau0823. doi: 10.1126/sciadv.aau0823.
[25]	ALBASH T and LIDAR D A. Demonstration of a scaling advantage for a quantum annealer over simulated annealing[J]. Physical Review X, 2018, 8(3): 031016. doi: 10.1103/PhysRevX.8.031016.
[26]	DENCHEV V S, BOIXO S, ISAKOV S V, et al. What is the computational value of finite-range tunneling?[J]. Physical Review X, 2016, 6(3): 031015. doi: 10.1103/PhysRevX.6.031015.
[27]	BOIXO S, SMELYANSKIY V N, SHABANI A, et al. Computational multiqubit tunnelling in programmable quantum annealers[J]. Nature Communications, 2016, 7(1): 10327. doi: 10.1038/ncomms10327.
[28]	SEBASTIAN A, LE GALLO M, KHADDAM-ALJAMEH R, et al. Memory devices and applications for in-memory computing[J]. Nature Nanotechnology, 2020, 15(7): 529–544. doi: 10.1038/s41565-020-0655-z.
[29]	YIN Xunzhao, QIAN Yu, VARDAR A, et al. Ferroelectric compute-in-memory annealer for combinatorial optimization problems[J]. Nature Communications, 2024, 15(1): 2419. doi: 10.1038/s41467-024-46640-x.
[30]	QIAN Yu, ZHAO Liang, MENG Fanzi, et al. Enhancing ConvNets with ConvFIFO: A crossbar PIM architecture based on kernel-stationary first-in-first-out dataflow[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2024, 32(9): 1640–1651. doi: 10.1109/TVLSI.2024.3409648.
[31]	JIANG Mingrui, SHAN Keyi, HE Chengping, et al. Efficient combinatorial optimization by quantum-inspired parallel annealing in analogue memristor crossbar[J]. Nature Communications, 2023, 14(1): 5927. doi: 10.1038/s41467-023-41647-2.
[32]	HUI Yajuan, LI Qingzhen, WANG Leimin, et al. In-memory Wallace tree multipliers based on majority gates within voltage-gated SOT-MRAM crossbar arrays[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2024, 32(3): 497–504. doi: 10.1109/TVLSI.2024.3350151.
[33]	VICTOR J, WANG Chunguang, and GUPTA S K. Memory technologies for crossbar array design: A comparative evaluation of their impact on DNN accuracy[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2025. doi: 10.1109/TCSI.2025.3550314.
[34]	SCHROEDER U, PARK M H, MIKOLAJICK T, et al. The fundamentals and applications of ferroelectric HfO₂[J]. Nature Reviews Materials, 2022, 7(8): 653–669. doi: 10.1038/s41578-022-00431-2.
[35]	SALAHUDDIN S, NI Kai, and DATTA S. The era of hyper-scaling in electronics[J]. Nature Electronics, 2018, 1(8): 442–450. doi: 10.1038/s41928-018-0117-x.
[36]	NEBASHI R, BANNO N, MIYAMURA M, et al. A 171k-LUT nonvolatile FPGA using Cu Atom-switch technology in 28nm CMOS[C]. Proceedings of 2020 30th International Conference on Field-Programmable Logic and Applications, Gothenburg, Sweden, 2020: 323–327. doi: 10.1109/FPL50879.2020.00060.
[37]	QIAN Yu, YANG Zeyu, NI Kai, et al. HyCiM: A hybrid computing-in-memory QUBO solver for general combinatorial optimization problems with inequality constraints[C]. Proceedings of the 61st ACM/IEEE Design Automation Conference, San Francisco, USA. 2024: 241. doi: 10.1145/3649329.3655989.
[38]	QIAN Yu, NI Kai, KAMPFE T, et al. C-Nash: A novel ferroelectric computing-in-memory architecture for solving mixed strategy Nash equilibrium[C]. Proceedings of the 61st ACM/IEEE Design Automation Conference, San Francisco, USA, 2024: 226. doi: 10.1145/3649329.3655988.
[39]	QIAN Yu, HUANG Ding, VARDAR A, et al. Ferroelectric compute-in-memory framework for solving pure and mixed strategy Nash equilibrium[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2025. doi: 10.1109/TCSI.2025.3548871.
[40]	QIAN Y, HUANG X, WANG R, et al. Device-algorithm co-design of ferroelectric compute-in-memory in-situ annealer for combinatorial optimization problems[C]. Proceedings of the 62nd ACM/IEEE Design Automation Conference, San Francisco, USA. 2025.
[41]	JIANG Zhouhang, XIAO Yi, CHATTERJEE S, et al. Asymmetric double-gate ferroelectric FET to decouple the tradeoff between thickness scaling and memory window[C]. Proceedings of 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, USA, 2022: 395–396. doi: 10.1109/VLSITechnologyandCir46769.2022.9830172.
[42]	CAI Jiahao, BARKAM H E, IMANI M, et al. A scalable 2T-1FeFET-based content addressable memory design for energy efficient data search[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2025, 44(5): 1760–1773. doi: 10.1109/TCAD.2024.3493000.
[43]	NI Chenyu, CHEN Sijie, LIU Chekai, et al. TAP-CAM: A tunable approximate matching engine based on ferroelectric content addressable memory[C]. Proceedings of the 43rd IEEE/ACM International Conference on Computer-Aided Design, New York, USA, 2024: 88. doi: 10.1145/3676536.3676699.
[44]	YIN Xunzhao, QIAN Yu, IMANI M, et al. Ferroelectric ternary content addressable memories for energy-efficient associative search[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2023, 42(4): 1099–1112. doi: 10.1109/TCAD.2022.3197694.
[45]	QIAN Yu, FAN Zhenhao, WANG Haoran, et al. Energy-aware designs of ferroelectric ternary content addressable memory[C]. Proceedings of 2021 Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 2021: 1090–1095. doi: 10.23919/DATE51398.2021.9474234.
[46]	YIN Xunzhao, MÜLLER F, HUANG Qingrong, et al. An ultracompact single-ferroelectric field-effect transistor binary and multibit associative search engine[J]. Advanced Intelligent Systems, 2023, 5(7): 2200428. doi: 10.1002/aisy.202200428.
[47]	LI Chao, SUN Chen, YANG Jianyi, et al. Multibit content addressable memory design and optimization based on 3-D nand-compatible IGZO flash[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2024, 32(8): 1380–1388. doi: 10.1109/TVLSI.2024.3392159.
[48]	YANG Zeyu, HUANG Qingrong, QIAN Yu, et al. Energy efficient dual designs of FeFET-based analog in-memory computing with inherent shift-add capability[C]. Proceedings of the 61st ACM/IEEE Design Automation Conference, San Francisco, USA, 2024: 290. doi: 10.1145/3649329.3655990.
[49]	LI Chao, HUANG Xuchu, XU Zhicheng, et al. High-performance in-memory Bayesian inference with multi-bit ferroelectric FET[J]. IEEE Transactions on Computers, 2025, 74(9): 2923–2935. doi: 10.1109/TC.2025.3576941.
[50]	LI Chao, XU Zhicheng, WEN Bo, et al. FeBiM: Efficient and compact Bayesian inference engine empowered with ferroelectric in-memory computing[C]. Proceedings of the 61st ACM/IEEE Design Automation Conference, San Francisco, USA, 2024: 246. doi: 10.1145/3649329.3656538.
[51]	YIN Xunzhao, HUANG Qingrong, BARKAM H E, et al. A homogeneous FeFET-based time-domain compute-in-memory fabric for matrix-vector multiplication and associative search[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2025, 44(5): 1856–1868. doi: 10.1109/TCAD.2024.3492994.
[52]	QIN Yixin, ZHAO Zijian, LIM S, et al. Understanding the memory window of ferroelectric FET and demonstration of 4.8-V memory window with 20-nm HfO₂[J]. IEEE Transactions on Electron Devices, 2024, 71(8): 4655–4663. doi: 10.1109/TED.2024.3418942.
[53]	HUANG X, DU H, ZHOU M, et al. VQT-CiM: Accelerating vector quantization enhanced transformer with ferroelectric compute-in-memory[C]. Proceedings of the 62nd ACM/IEEE Design Automation Conference, San Francisco, USA. 2025.
[54]	LU C C, SHIH Y C, CHANG C Y, et al. Demonstration of ferroelectric FET memory with oxide semiconductor channel to achieve smallest cell area 0.009 μm² and high endurance for non-volatile high-bandwidth memory applications[C]. Proceedings of 2024 IEEE International Electron Devices Meeting, San Francisco, USA, 2024: 1–4. doi: 10.1109/IEDM50854.2024.10873402.
[55]	VAN LAARHOVEN P J M and AARTS E H L. Simulated Annealing: Theory and Applications[M]. Dordrecht: Springer, 1987.
[56]	NI Kai, JERRY M, SMITH J A, et al. A circuit compatible accurate compact model for ferroelectric-FETs[C]. Proceedings of 2018 IEEE Symposium on VLSI Technology, Honolulu, USA, 2018: 131–132. doi: 10.1109/VLSIT.2018.8510622.
[57]	POREMBA M, MITTAL S, LI Dong, et al. DESTINY: A tool for modeling emerging 3D NVM and eDRAM caches[C]. Proceedings of 2015 Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 2015: 1543–1546. doi: 10.7873/DATE.2015.0733.
[58]	Stanford max-cut dataset[EB/OL]. https://web.stanford.edu/~yyye/yyye/Gset/.
[59]	HUSSAIN M A, LIN S W, and TSAI T H. An area-efficient and high throughput hardware implementation of exponent function[C]. Proceedings of 2022 IEEE International Symposium on Circuits and Systems, Austin, USA, 2022: 3369–3372. doi: 10.1109/ISCAS48785.2022.9937238.
[60]	Quadratic knapsack problem dataset[EB/OL]. http://cedric.cnam.fr/soutif/QKP/QKP.html.
[61]	KHAN F S, OKRUT O, CANNON K, et al. Calculating Nash equilibrium on quantum annealers[J]. Annals of Operations Research, 2025, 346(2): 1109–1126. doi: 10.1007/s10479-023-05700-z.