Design of a Bilinear Pairing Coprocessor Based on RISC-V Instruction Extension
-
摘要: 双线性对运算是基于身份的标识密码算法的核心运算，而在边缘设备中实现该运算需要在性能与面积两方面进行折衷。采用指令扩展方式进行软硬件协同设计是具备灵活性和可扩展性的设计方式，但在双线性对运算方面的研究忽略了数据交互过程的时间损耗。该文结合双线性对算法与软硬件协同设计的特点，提出了适配总线传输的模乘运算模式用于减少数据交互过程中的时间损耗，同时设计适配该模式的模乘单元与阔域运算的时序排布，完成基于国产RISC-V处理器进行素数域运算和扩域运算的自定义指令扩展，并使用C语言调度硬件指令实现软硬件协同设计方案。所设计的协处理器在Xilinx ZYNQ-7000 FPGA平台上实现，共消耗8.3k个Slice与134个 数字处理单元 (DSP)，素数域模乘的执行时间为0.3 μs，2次扩域模乘的执行时间为0.6 μs，双线性对的执行时间约为17.5 ms。实验结果表明，该文设计的协处理器兼顾性能与面积，与同类设计在性能上相比至少提升7%， 能够高效地实现双线性对运算。Abstract:
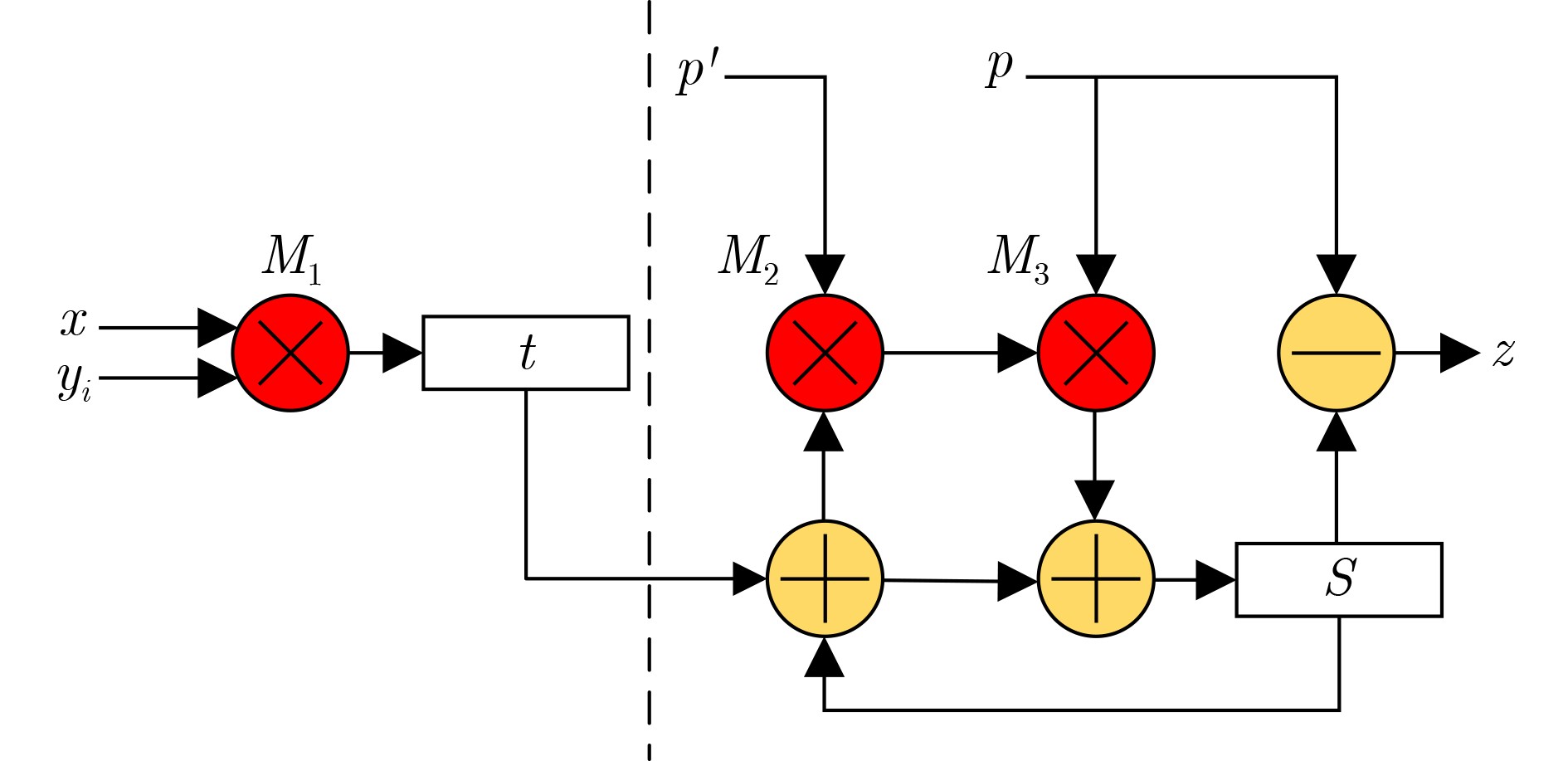
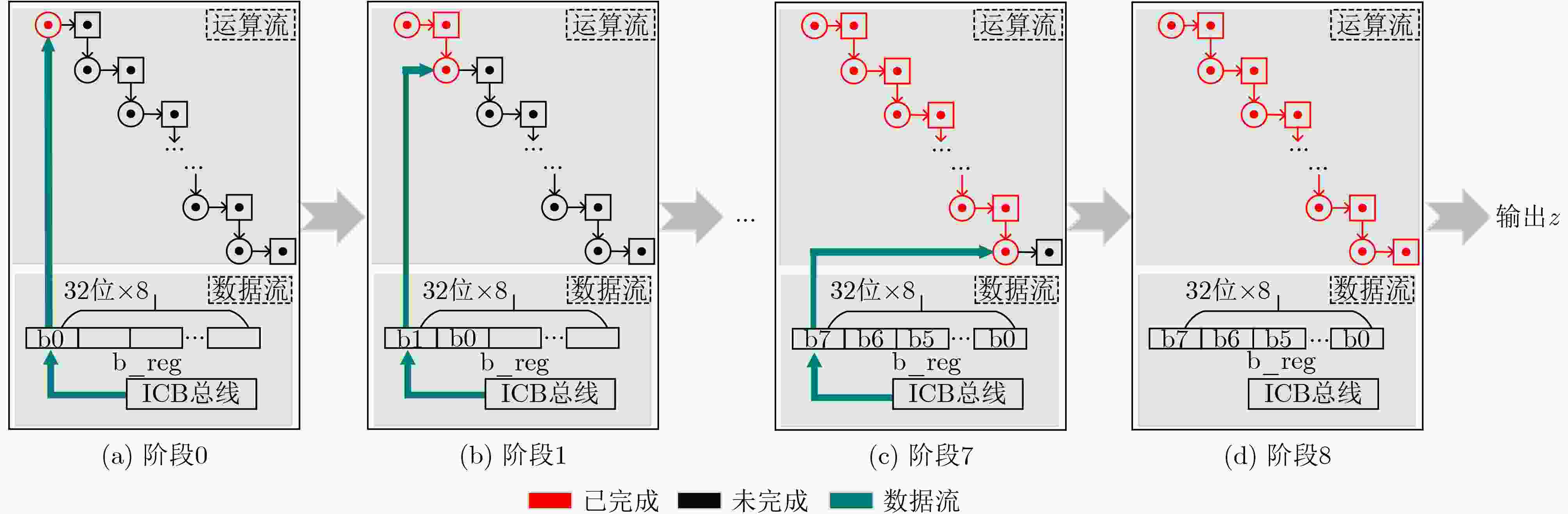
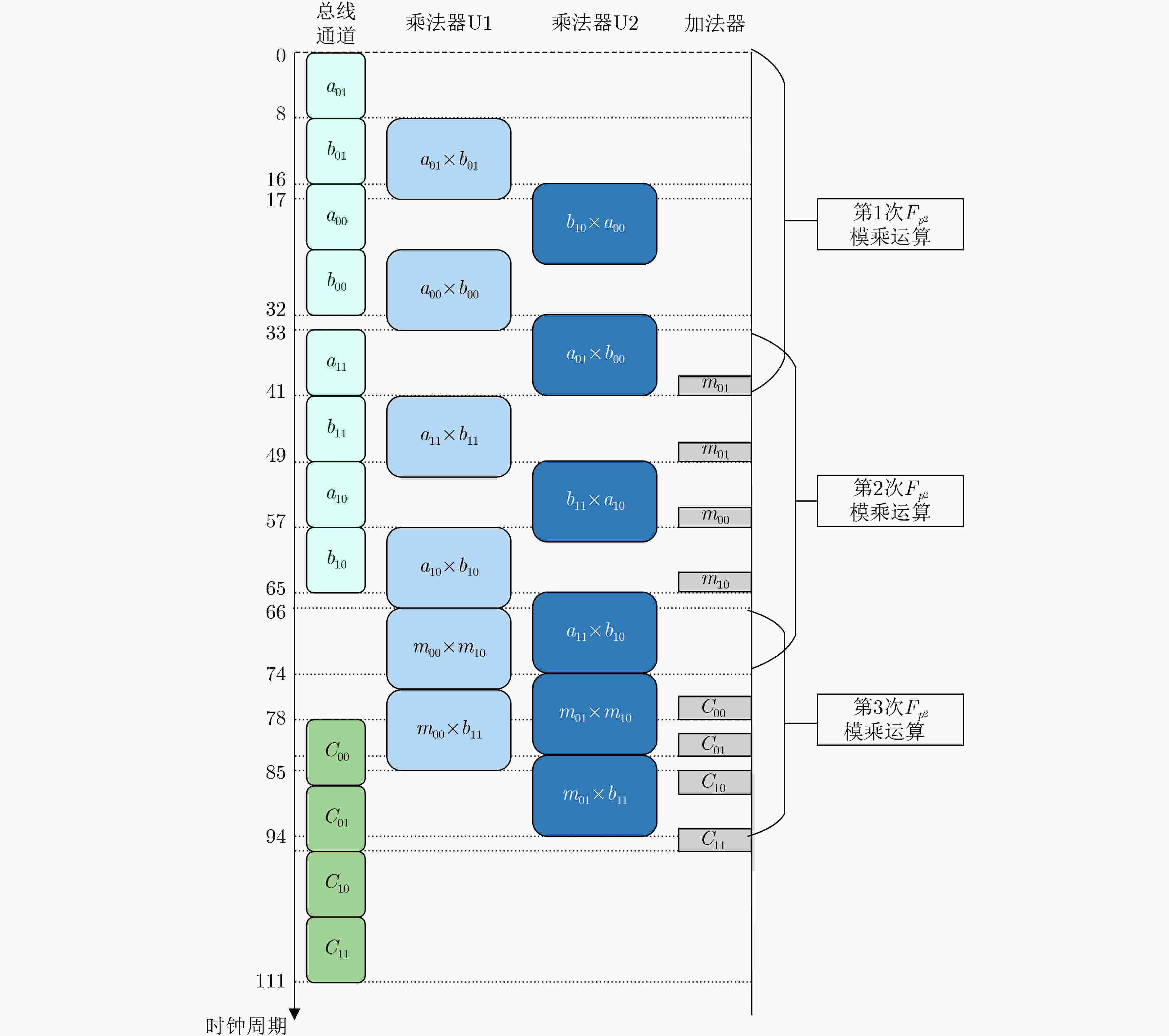
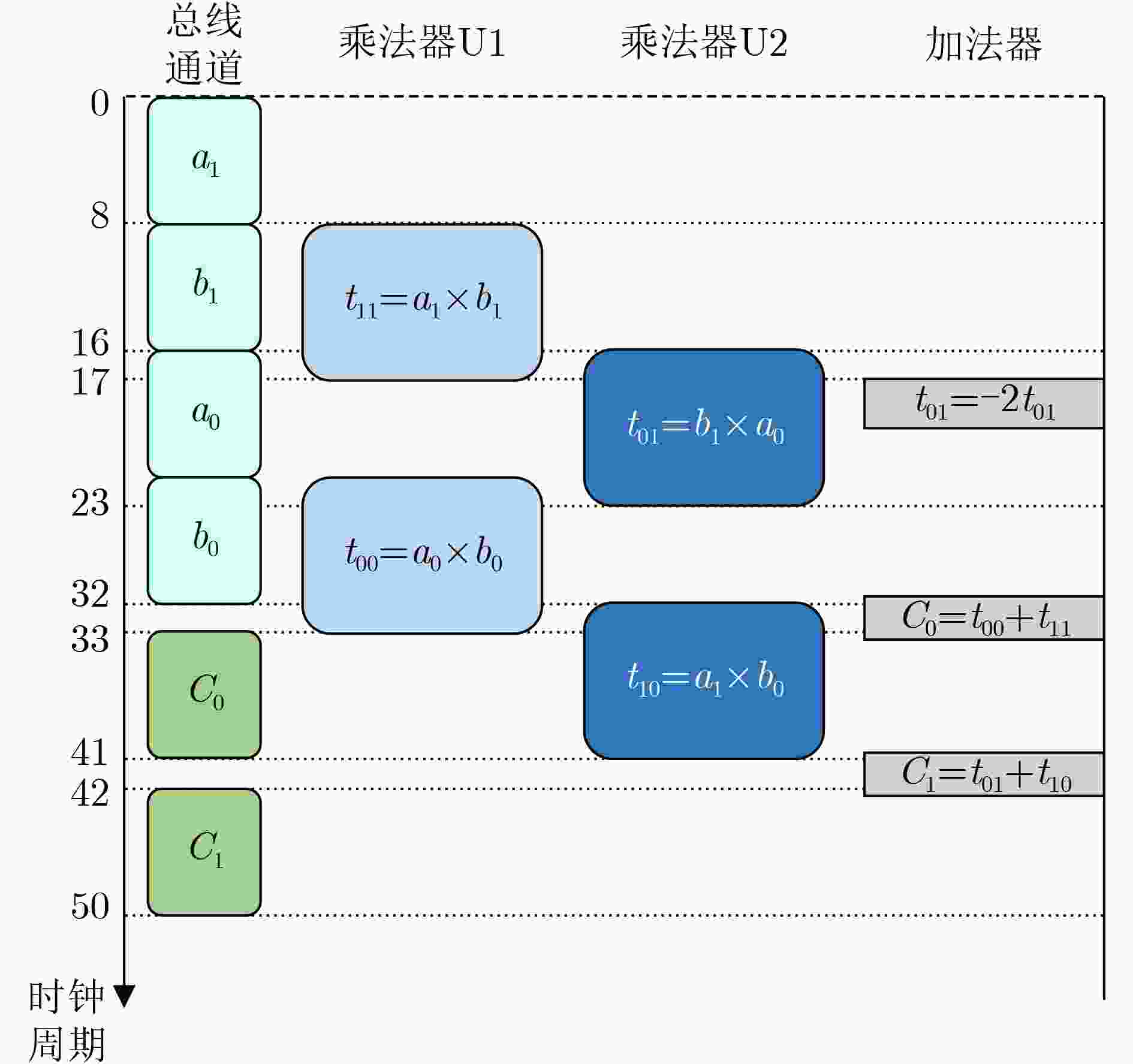
Objective Bilinear pairing operations are fundamental to modern cryptography, forming the basis of advanced systems applied in identity authentication, key exchange, digital signatures, and attribute-based encryption. However, hardware implementations of bilinear pairings face two major challenges: their high computational complexity results in considerable hardware resource consumption, and traditional Field-Programmable Gate Array (FPGA)-based approaches provide limited flexibility. To address these limitations, this study proposes a solution that integrates the RISC-V architecture with Identity-Based Cryptography (IBC) algorithms through instruction set extension and hardware–software co-design. The proposed approach reduces hardware resource requirements, enhances system flexibility, and enables efficient implementation of cryptographic algorithms. Methods The methodology is composed of three main steps. First, conventional state machine-based control logic is replaced by an extended RISC-V instruction set. Six custom instructions are introduced to control arithmetic units for fundamental operations, which transforms the hardware implementation of bilinear pairings from control-intensive to data-intensive circuits, thereby improving hardware resource utilization. Second, to mitigate the bottleneck caused by the bus width limitation of RISC-V, a modular multiplication unit and a bus-efficient modular multiplication mode are designed. By adjusting algorithmic timesteps and employing a small number of on-chip temporary registers, this mode integrates data transmission with computation, allowing transmission and computation cycles to overlap. As a result, the proportion of computation cycles in the overall cycle count is increased, improving system efficiency. Third, a hardware–software co-design strategy is adopted, in which higher-level algorithmic flows are scheduled in software to invoke hardware instructions, thus enhancing system flexibility. Results and Discussions (1) Compared with conventional data-intensive circuits, the proposed modular multiplication mode ( Fig. 5 ) effectively reduces the proportion of data transmission cycles in extension field operations. Furthermore, timing optimization of modular multiplication in the quartic extension field (Fig. 6 ) and the quadratic extension field (Fig. 7 ) further reduces transmission cycles, thereby improving overall system performance. (2) Relative to FPGA-based implementations of bilinear pairing, the proposed design achieves superior performance in modular multiplication within both the prime field and the quadratic extension field (Table 3 ). It also shows a clear advantage in terms of Area–Time Product (ATP) for complete bilinear pairing operations. In addition, the design supports flexible adjustment of instruction invocation sequences to accommodate the requirements of different IBC algorithms, leading to a marked improvement in system flexibility.Conclusions This paper presents a RISC-V coprocessor that supports bilinear pairing operations for IBC algorithms, addressing the limitations of conventional approaches characterized by high hardware resource consumption, low system utilization, and limited flexibility. A method targeting bus transmission bottlenecks is proposed, which effectively reduces transmission cycle ratios in modular multiplication for quadratic and quartic extension fields. System flexibility is further enhanced by adjusting instruction scheduling to meet the requirements of different IBC algorithms. Future work will focus on exploring pipelined operation modes for more advanced algorithms, using small temporary register groups to further reduce transmission ratios, and achieving cost-effective optimization in data-intensive circuits with balanced area efficiency and computational performance. -
Key words:
- RISC-V /
- Bilinear pairing operation /
- Coprocessor /
- Modular multiplication
-
1 双线性对运算
输入：$ P\in E\left({F}_{q}\right)\left[r\right],Q\in {E}^{{'}}\left({F}_{{q}^{2}}\right)\left[r\right],a=6t+2 $ 输出：$ {f=R}_{a}(Q,P) $ (1) $ a=\displaystyle\sum\nolimits_{i=0}^{L-1}{a}_{i}{2}^{i} $, $ {a}_{L-1}=1 $; (2) $ T=Q,f=1 $; (3) $ \bf{f}\bf{o}\bf{r} $ $ i=L-2\mathrm{t}\mathrm{o}0 $ do (3.1) $ f={f}^{2}*{g}_{T,T}\left(P\right),T=\left[2\right]T; $ (3.2) if $ {a}_{i}=1 $ $ \bf{d}\bf{o} $ $ f=f*{g}_{T,Q}\left(P\right),T=T+Q $; (4) $ {Q}_{1}={\pi }_{q}\left(Q\right),{Q}_{2}={\pi }_{{q}^{2}}\left(Q\right) $; (5) $ f=f*{g}_{T,{Q}_{1}}\left(P\right),T=T+{Q}_{1} $; (6) $ f=f*{g}_{T,{-Q}_{2}}\left(P\right),T=T-{Q}_{2} $; (7) $ f={f}^{({q}^{12}-1)/r} $ (8) $ \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}f $ 
下载: 导出CSV
表 1 自定义指令
指令 功能 func7 func3 opcode $ \mathrm{f}\mathrm{p}\_\mathrm{a}\mathrm{d}\mathrm{d} $ 素数域模加 0000000 111 1111011 $ \mathrm{f}\mathrm{p}\_\mathrm{s}\mathrm{u}\mathrm{b} $ 素数域模减 0000001 111 1111011 $ \mathrm{f}\mathrm{p}\_\mathrm{i}\mathrm{n}\mathrm{v} $ 素数域模逆 0000110 111 1111011 $ \mathrm{f}\mathrm{p}\_\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t} $ 素数域模乘 0000010 111 1111011 $ \mathrm{f}{\mathrm{p}}_{2}\_\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t} $ 2次扩域模乘 0000101 111 1111011 $ \mathrm{f}{\mathrm{p}}_{4}\_\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t} $ 4次扩域模乘 0001000 111 1111011
下载: 导出CSV
2 高基流水线Montgomery模乘算法
输入：模数$ p $且$ \mathrm{gcd}\left(p,2\right)=1, -p\times p'\mathrm{m}\mathrm{o}\mathrm{d}{2}^{\omega }=1, $被乘数
$ x\ge 0, $乘数$ y=\displaystyle\sum\nolimits_{i=0}^{n-1}{y}_{\left(i\right)}{2}^{\omega j},n=256/\omega $ 输出：$ z=xy{2}^{-n}\left(\mathrm{m}\mathrm{o}\mathrm{d}p\right)(0\le z < 2p) $ (1) $ {S}_{0}=0,q=0; $ (2) $ {t}_{0}=x{y}_{0}; $ (3) $ \bf{f}\bf{o}\bf{r}\;i=1\;\bf{t}\bf{o}\;n-1\;\bf{d}\bf{o} $ (4) $ {t}_{i}=x{y}_{i}; $ (5) $ u={S}_{i-1}+{t}_{i-1}; $ (6) $ q=\left(\left(u\mathrm{m}\mathrm{o}\mathrm{d}{2}^{\omega }\right)\times p'\right)\mathrm{m}\mathrm{o}\mathrm{d}{2}^{\omega }; $ (7) $ {S}_{i}=(q\times p+u)/{2}^{\omega }; $ (8) $ \bf{e}\bf{n}\bf{d}\;\bf{f}\bf{o}\bf{r} $ (9) $ \bf{i}\bf{f}\;{S}_{i} > p $ (10) $ z={S}_{i}-p; $ (11) $ \bf{e}\bf{l}\bf{s}\bf{e} $ (12) $ z={S}_{i}; $ (13) $ \bf{e}\bf{n}\bf{d}\;\bf{i}\bf{f} $ (14) $ \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\;z; $
下载: 导出CSV
表 2 4次扩域模乘实现方式对比
模乘法器数量 LUT DSP 周期数 时间(μs) ATP 2个 8330 134 111 1.44 0.158 1个 7908 67 140 1.82 0.168
下载: 导出CSV
表 4 双线性对运算性能参数表
平台 面积 频率(MHz) 周期(×103) 时间(ms) ATP 本文 Zynq-7000 8k Slices, 134 DSPs 77 692.7 8.9 0.97 文献[10] Virtex-5 2k Slices, 17 DSPs 100 11 228.2 112.3 2.62 文献[11] Virtex-7 28k Slices, 128 DSPs 115 394.8 3.4 1.04 文献[12] Zynq-7000 85k Slices, 220 DSPs 667 11 112.0 16.7 2.15 文献[18] Virtex-7 210k Slices 165 742.5 4.6 9.42
下载: 导出CSV
-
[1] SHAMIR A. Identity-based cryptosystems and signature schemes[M]. BLAKLEY G R and CHAUM D. Advances in Cryptology. Berlin, Heidelberg: Springer, 1985: 47–53. doi: 10.1007/3-540-39568-7_5. [2] 袁峰, 程朝辉. SM9标识密码算法综述[J]. 信息安全研究, 2016, 2(11): 1008–1027.YUAN Feng and CHENG Zhaohui. Overview on SM9 identity based cryptographic algorithm[J]. Journal of Information Security Research, 2016, 2(11): 1008–1027. [3] BEUCHAT J L, GONZÁLEZ-DÍAZ J E, MITSUNARI S, et al. High-speed software implementation of the optimal ate pairing over Barreto–Naehrig curves[C]. 4th International Conference on Pairing-Based Cryptography - Pairing 2010, Yamanaka Hot Spring, Japan, 2010: 21–39. doi: 10.1007/978-3-642-17455-1_2.(查阅网上资料,请核对出版城市信息). [4] NAEHRIG M, NIEDERHAGEN R, and SCHWABE P. New software speed records for cryptographic pairings[C]. First International Conference on Progress in Cryptology – LATINCRYPT 2010, Puebla, Mexico, 2010: 109–123. doi: 10.1007/978-3-642-14712-8_7. [5] GRABHER P, GROßSCHÄDL J, and PAGE D. On software parallel implementation of cryptographic pairings[C]. 15th Annual International Workshop on Selected Areas in Cryptography, Sackville, Canada, 2009: 35–50. doi: 1 0.1007/978-3-642-04159-4_3. [6] KAMMLER D, ZHANG Diandian, SCHWABE P, et al. Designing an ASIP for cryptographic pairings over Barreto-Naehrig curves[C]. 11th International Workshop on Cryptographic Hardware and Embedded Systems - CHES 2009, Lausanne, Switzerland, 2009: 254–271. doi: 10.1007/978-3-642-04138-9_19. [7] CUEVAS-FARFÁN E, MORALES-SANDOVAL M, CUMPLIDO R, et al. A programmable FPGA-based cryptoprocessor for bilinear pairings over F2m[C]. 2013 8th International Workshop on Reconfigurable and Communication-Centric Systems-on-Chip (ReCoSoC), Darmstadt, Germany, 2013: 1–8. doi: 10.1109/ReCoSoC.2013.6581528. [8] GHOSH S, MUKHOPADHYAY D, and ROYCHOWDHURY D. High speed flexible pairing cryptoprocessor on FPGA platform[C]. 4th International Conference on Pairing-Based Cryptography - Pairing 2010, Yamanaka Hot Spring, Japan, 2010: 450–466. doi: 10.1007/978-3-642-17455-1_28. (查阅网上资料,请核对出版城市信息). [9] DAM D T, NGUYEN T H, TRAN T H, et al. High-efficiency multi-standard polynomial multiplication accelerator on RISC-V SoC for post-quantum cryptography[J]. IEEE Access, 2024, 12: 195015–195031. doi: 10.1109/ACCESS.2024.3520592. [10] AZZOUZI O, ANANE M, KOUDIL M, et al. Novel area-efficient and flexible architectures for optimal ate pairing on FPGA[J]. The Journal of Supercomputing, 2024, 80(2): 2633–2659. doi: 10.1007/s11227-023-05578-5. [11] WANG Tengfei, GUO Wei, and WEI Jizeng. Highly-parallel hardware implementation of optimal ate pairing over Barreto-Naehrig curves[J]. Integration, 2019, 64: 13–21. doi: 10.1016/j.vlsi.2018.04.013. [12] MÁRQUEZ R C, SARMIENTO A J C, and SÁNCHEZ-SOLANO S. Implementing cryptographic pairings on ARM dual-core processors[J]. IEEE Latin America Transactions, 2020, 18(2): 232–240. doi: 10.1109/tla.2020.9085275. [13] CHOI E, PARK J, HAN K, et al. AESware: Developing AES-enabled low-power multicore processors leveraging open RISC-V cores with a shared lightweight AES accelerator[J]. Engineering Science and Technology, An International Journal, 2024, 60: 101894. doi: 10.1016/j.jestch.2024.101894. [14] 王明登, 严迎建, 郭朋飞, 等. 基于RISC-V指令扩展方式的国密算法SM2、SM3和SM4的高效实现[J]. 电子学报, 2024, 52(8): 2850–2865. doi: 10.12263/DZXB.20230391.WANG Mingdeng, YAN Yingjian, GUO Pengfei, et al. Efficient implementation of national security algorithms SM2, SM3 and SM4 based on RISC-V instruction extension method[J]. Acta Electronica Sinica, 2024, 52(8): 2850–2865. doi: 10.12263/DZXB.20230391. [15] KARMAKAR A, SÁNCHEZ-SOLANO S, MARTÍNEZ-RODRÍGUEZ M C, et al. HW/SW implementation of RSA digital signature on a RISC-V-based system-on-chip[C]. 38th Conference on Design of Circuits and Integrated Systems (DCIS), Málaga, Spain, 2023: 1–6. doi: 10.1109/DCIS58620.2023.10335970. [16] PAN Lihang, TU Guoqing, LIU Shubo, et al. A lightweight AES coprocessor based on RISC-V custom instructions[J]. Security and Communication Networks, 2021, 2021: 9355123. doi: 10.1155/2021/9355123. [17] 刘志伟, 刘雷波, 黄海, 等. 面向多曲线的通用高性能ECC处理器设计[J]. 电子学报, 2023, 51(6): 1562–1571. doi: 10.12263/DZXB.20210967.LIU Zhiwei, LIU Leibo, HUANG Hai, et al. Multi-curve-oriented general high-performance ECC processor design[J]. Acta Electronica Sinica, 2023, 51(6): 1562–1571. doi: 10.12263/DZXB.20210967. [18] DONG Xiuze, GAO Mingze, MA Xujian, et al. An implementation of R-ate pairing based on FPGA[C]. 3rd International Conference on Big Data, Information and Computer Network, Sanya, China, 2024: 167–173. doi: 10.1109/BDICN62775.2024.00041. -
图(7) / 表(6)
计量
- 文章访问数: 27
- HTML全文浏览量: 11
- PDF下载量: 2
- 被引次数: 0
下载:
