Hybrid Vibration Isolation Design Based on Piezoelectric Actuator and Quasi-zero Stiffness System
-
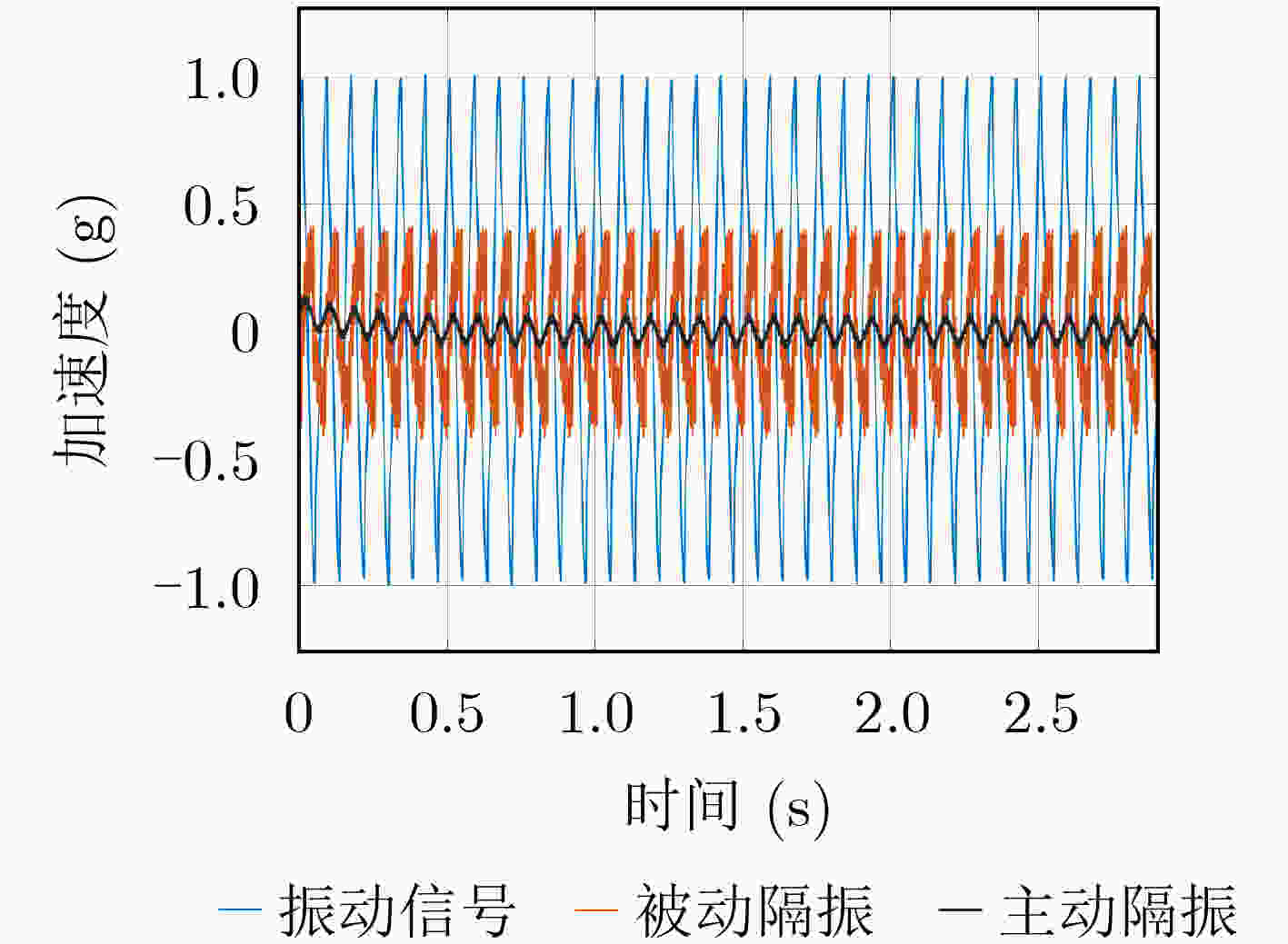
摘要: 低频振动对于精密仪器有着不容忽视的危害，通过弹簧的特殊排列可以实现近零刚度的非线性力学特性，不仅能够显著提高低频隔振效果，而且对于高频率的振动也有一定的隔离效果。然而，基于准零刚度的纯被动系统在动态响应上存在局限性，对振幅的依赖较大。因此，该文提出一种压电作动器的准零刚度混合主被动隔振系统，通过主动控制调节，从而增强混合系统整体的动态性能。首先，搭建基于压电作动器的准零刚度混合系统，由线性弹簧组成的准零刚度装置作为被动隔振装置，压电作动器作为主动隔振装置；其次，提出了一种改进的Bouc-Wen(B-W)模型，通过逆模型对其迟滞非线性进行补偿，对隔振对象施加精准的主动控制；最后，建立系统的动力学方程，对外界振动采用带Luenberger的滑模观测器的自适应滑模控制，提高系统的隔振性能。通过隔振控制实验验证，相比于单一被动隔振装置隔振效果提高35%左右。
-
关键词:
- 主被动隔振 /
- 改进的Bouc-Wen模型 /
- 准零刚度 /
- 压电作动器
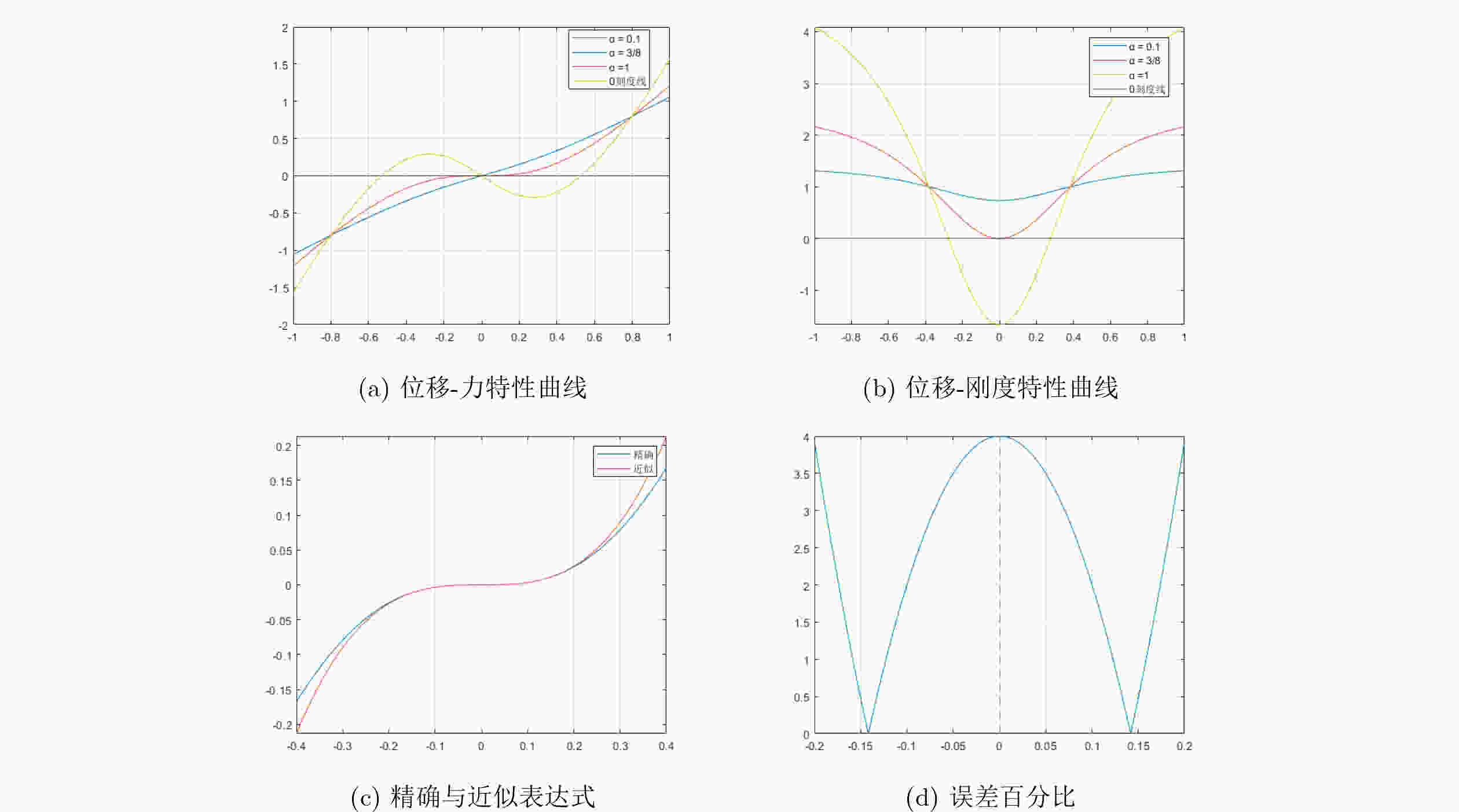
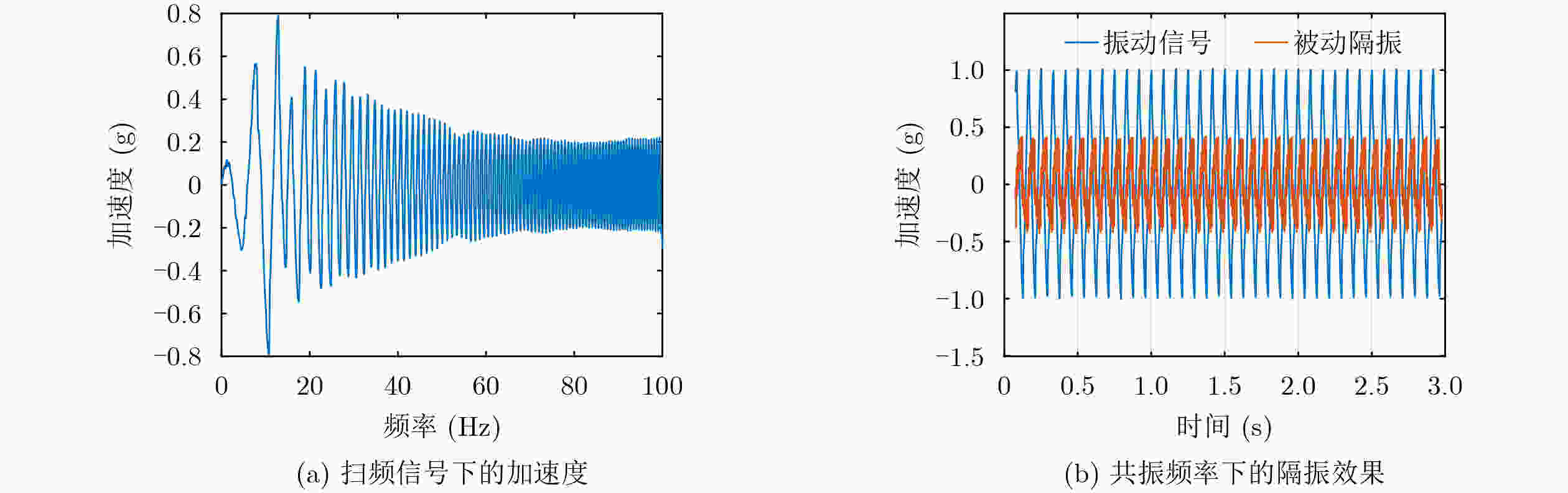
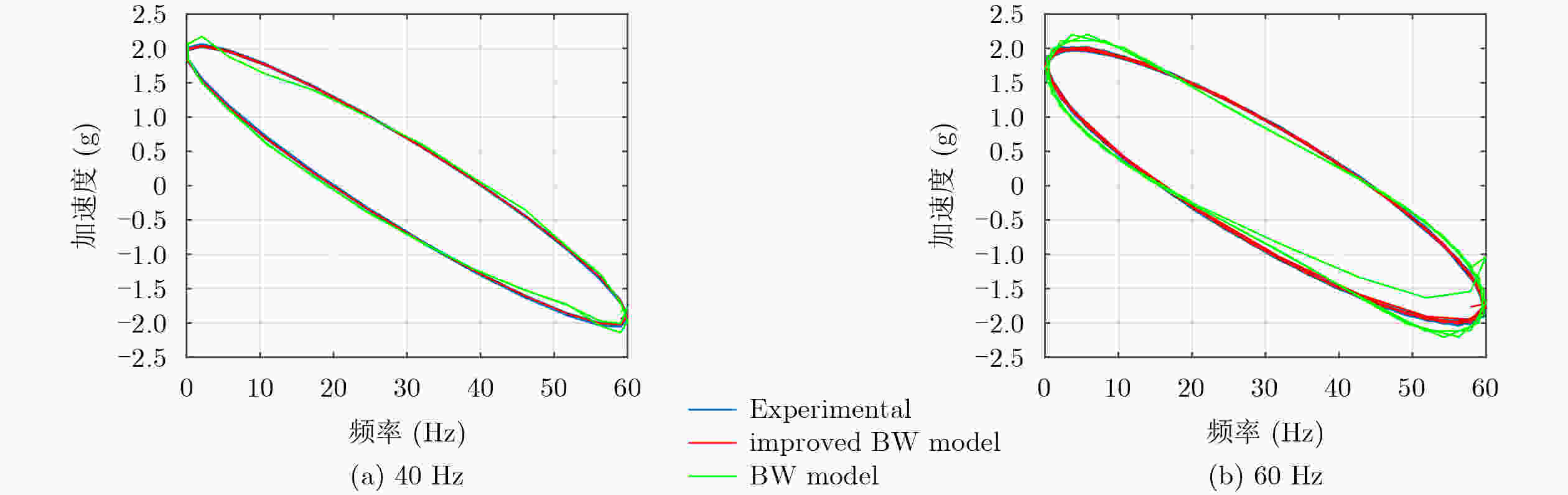
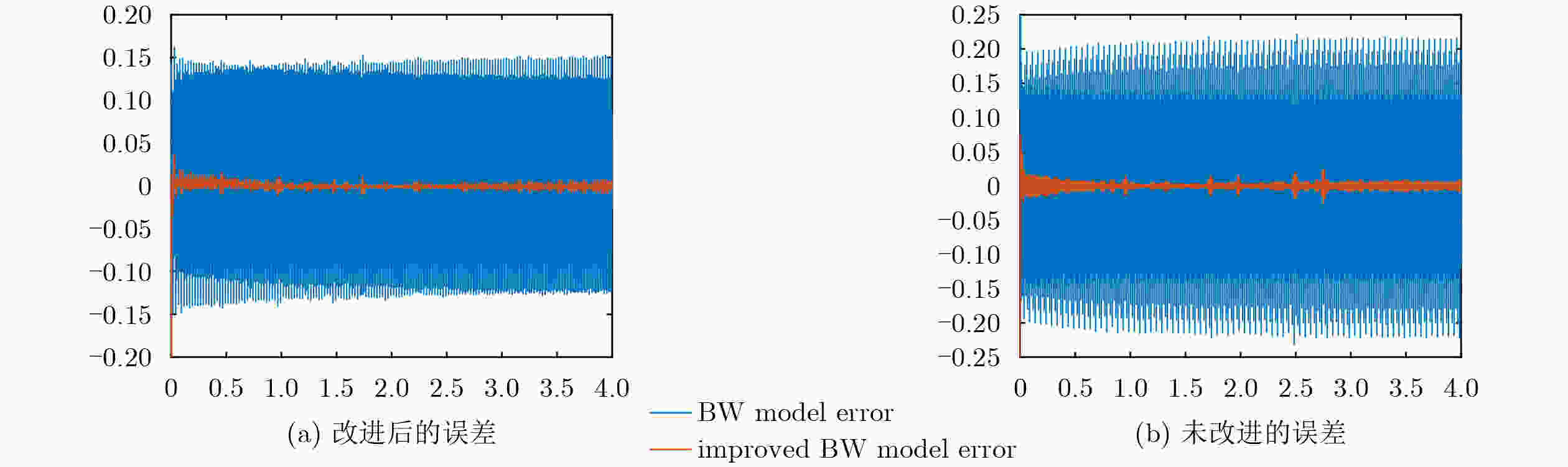
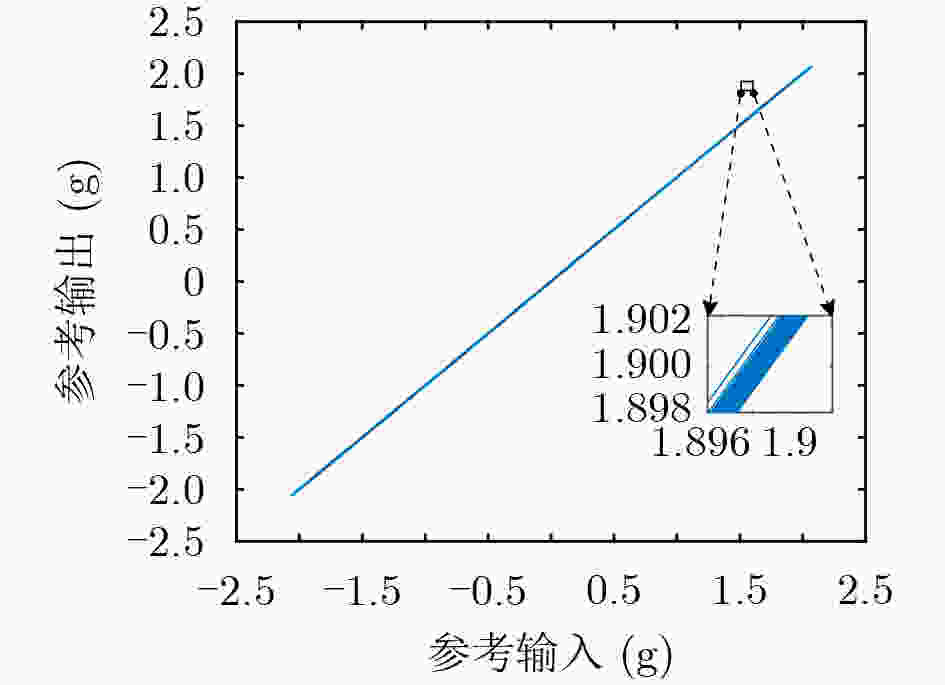
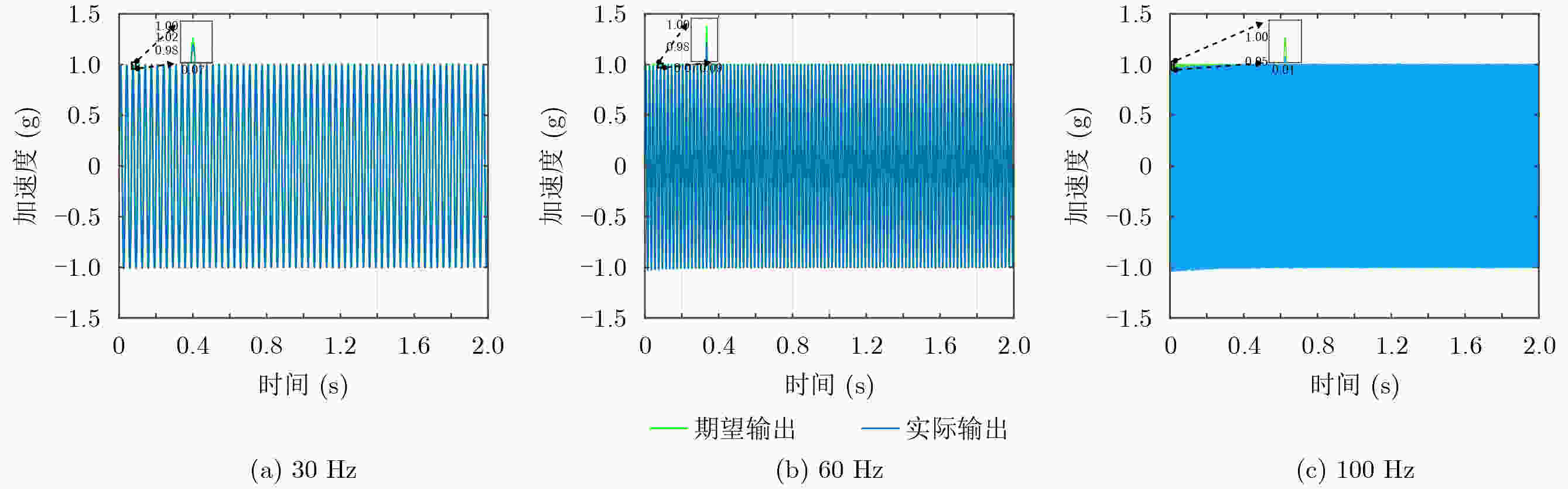
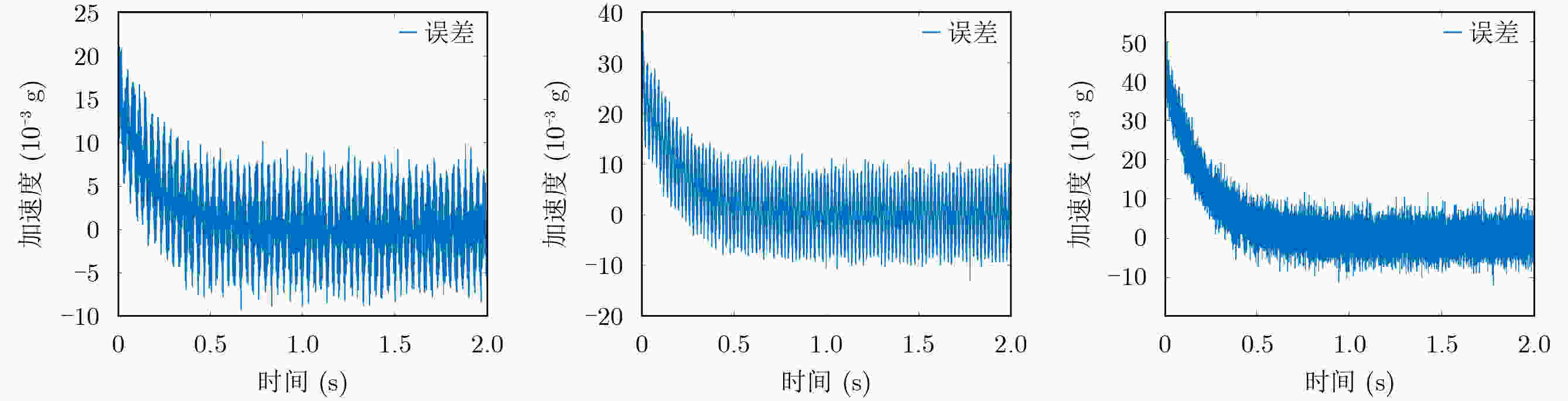
Abstract:Objective With the rapid advancement of technology, precision instruments are increasingly demanding higher standards for vibration environments. Traditional passive vibration isolation methods can no longer meet these requirements. Vibrations within laboratory environments, caused by activities such as personnel movement, machinery operation, and vehicle transit, can propagate over greater distances and penetrate thicker materials. When transmitted to platforms supporting precision instruments, these vibrations can compromise their accuracy, stability, and reliability. For traditional passive vibration isolation methods, such as rubber and springs, their effectiveness in isolating low-frequency and small-amplitude vibrations is limited. While quasi-zero-stiffness (QZS) systems offer some benefits for low-frequency vibration isolation, their performance is amplitude-dependent and requires high installation precision. Active vibration isolation, on the other hand, involves installing isolation devices between the vibration source and the supporting structure, leveraging active control strategies to achieve vibration suppression. Piezoelectric ceramics, as a class of smart materials characterized by high precision and rapid response characteristics, have been widely utilized in active vibration isolation systems. However, purely active vibration isolation demonstrates potential limitations: due to constraints in sensor sampling rates and actuator response speeds, their effectiveness at high frequencies may be inferior to passive vibration isolation. Moreover, in scenarios involving high-frequency or large-amplitude vibrations, actuators exhibit significantly higher energy consumption. Additionally, the inherent hysteresis properties of piezoelectric ceramics pose significant challenges to control precision. Therefore, the combination of active and passive vibration isolation technologies plays a critical role in ensuring the stability of precision instruments in laboratory environments. Methods This paper presents a hybrid vibration isolation design method that integrates piezoelectric actuators with a QZS mechanism. First, a piezoelectric actuator is developed using a stacked piezoelectric ceramic structure to provide the required output force and displacement. A preload is applied through elastic spacers to improve its operational stability and linearity. Second, the QZS system is constructed by combining positive- and negative-stiffness elements, thereby achieving high static stiffness while maintaining low dynamic stiffness. To address the hysteresis nonlinearity inherent in piezoelectric actuators, an improved Bouc–Wen model is employed for characterization, and its corresponding inverse model is formulated to enable hysteresis compensation. Finally, the piezoelectric actuator is integrated with the QZS mechanism, and the vibration isolation performance of the proposed hybrid system is evaluated through numerical simulations. Results and Discussions This paper designs an active-passive vibration isolation device, consisting of a QZS system made of linear springs and a piezoelectric actuator formed by a piezoelectric stack ( Fig.9a ). Since the traditional Bouc-Wen (B-W) algorithm cannot accurately capture the dynamic relationship between acceleration and voltage, this study introduces a voltage derivative term (Algorithm 13) into the traditional algorithm. This modification enables a more precise characterization of the force-voltage relationship and enhances the adaptability of the model, allowing it to accurately describe the acceleration-voltage relationship under a wider range of conditions. The parameters of the forward model are identified using the differential evolution algorithm (Table 1 ). An inverse model is constructed using the direct inversion method, with its parameters identified by the differential evolution algorithm (Table 2 ). The forward model and the inverse model are cascaded to compensate for the hysteresis phenomenon(Fig. 8 ). The dynamic equations of the QZS vibration isolation system and the linearized piezoelectric actuator are derived (Algorithm 16). Finally, an adaptive sliding mode controller based on a Luenberger sliding mode observer is proposed to control the vibration signal (Algorithm 18～ Algorithm 30), and the performance of active vibration isolation is demonstrated.Conclusions The hybrid vibration isolation design proposed in this study combines the passive vibration isolation characteristics of the QZS system with the active control advantages of the piezoelectric actuator, providing a new solution for the vibration isolation of precision instruments. This design not only improves the fitting effect of the hysteresis of piezoelectric ceramics. The hysteresis nonlinearity of the voltage-acceleration relationship is compensated for by establishing an inverse model, and then derives the dynamic model of the passive-active vibration isolation. By controlling the vibration signal with adaptive sliding mode control based on a Luenberger sliding mode observer, the vibration isolation effect is achieved, and the obtained vibration isolation effect has important application value and research significance. -
表 2 辨识结果
参数 $k$ $\alpha $ $\beta $ $\gamma $ $p$ $b$ 值 – 2.4179 2.8832 9.5865 – 4.3025 – 0.0039 0.9871 
下载: 导出CSV
-
[1] 孙秀婷, 钱佳伟, 齐志凤, 等. 非线性隔振及时滞消振方法研究进展[J]. 力学进展, 2023, 53(2): 308–356. doi: 10.6052/1000-0992-22-048.SUN Xiuting, QIAN Jiawei, QI Zhifeng, et al. Review on research progress of nonlinear vibration isolation and time-delayed suppression method[J]. Advances in Mechanics, 2023, 53(2): 308–356. doi: 10.6052/1000-0992-22-048. [2] NISTRI F, COSENTINI R M, DAL POGGETTO V F, et al. Attenuation of bulk waves using locally resonant soil-coupled metabarriers[J]. Journal of Physics D: Applied Physics, 2025, 58(4): 045502. doi: 10.1088/1361-6463/ad8ad0. [3] 刘涛, 李爱群. 准零刚度隔振系统的分析及研究进展[J]. 东南大学学报: 自然科学版, 2023, 53(6): 997–1012. doi: 10.3969/j.issn.1001-0505.2023.06.006.LIU Tao and LI Aiqun. An overview of research progress on quasi-zero stiffness vibration isolation systems[J]. Journal of Southeast University: Natural Science Edition, 2023, 53(6): 997–1012. doi: 10.3969/j.issn.1001-0505.2023.06.006. doi: 10.3969/j.issn.1001-0505.2023.06.006. [4] LI Xuan, DING Bingxiao, RAN Jinchao, et al. Design and characterization of a compact tripod quasi-zero-stiffness device for isolating low-frequency vibrations[J]. Precision Engineering, 2024, 91: 632–643. doi: 10.1016/j.precisioneng.2024.10.013. [5] MENG Qingye, HOU Lei, LIN Rongzhou, et al. Accurate nonlinear dynamic characteristics analysis of quasi-zero-stiffness vibration isolator via a modified incremental harmonic balance method[J]. Nonlinear Dynamics, 2024, 112(1): 125–150. doi: 10.1007/s11071-023-09036-y. [6] GATTI G. A nonlinear quasi-zero stiffness vibration isolator with quintic restoring force characteristic: A fundamental analytical insight[J]. Journal of Vibration and Control, 2024, 30(17/18): 4185–4198. doi: 10.1177/10775463231205806. [7] ZENG Rong, WEN Guilin, ZHOU Jiaxi, et al. Experimental investigation of a non-smooth quasi-zero-stiffness isolator[J]. Acta Mechanica Sinica, 2023, 39(6): 522415. doi: 10.1007/s10409-023-22415-x. [8] CARRELLA A, BRENNAN M J, WATERS T P, et al. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness[J]. International Journal of Mechanical Sciences, 2012, 55(1): 22–29. doi: 10.1016/j.ijmecsci.2011.11.012. [9] 杨兆豪, 帅长庚, 李步云. 一种基于五弹簧模型的准零刚度隔振装置特性分析[J]. 舰船科学技术, 2023, 45(18): 77–84. doi: 10.3404/j.issn.1672-7649.2023.18.013.YANG Zhaohao, SHUAI Changgeng, and LI Buyun. Analysis of a five-spring vibration isolator with quasi-zero-stiffness characteristic[J]. Ship Science and Technology, 2023, 45(18): 77–84. doi: 10.3404/j.issn.1672-7649.2023.18.013. [10] 徐道临, 张月英, 周加喜, 等. 一种准零刚度隔振器的特性分析与实验研究[J]. 振动与冲击, 2014, 33(11): 208–213. doi: 10.13465/j.cnki.jvs.2014.11.036.XU Daolin, ZHANG Yueying, ZHOU Jiaxi, et al. Characteristic analysis and experimental investigation for a vibration isolator with quasi-zero stiffness[J]. Journal of Vibration and Shock, 2014, 33(11): 208–213. doi: 10.13465/j.cnki.jvs.2014.11.036. [11] YUN Hai, LIU Lei, LI Qing, et al. Investigation on two-stage vibration suppression and precision pointing for space optical payloads[J]. Aerospace Science and Technology, 2020, 96: 105543. doi: 10.1016/j.ast.2019.105543. [12] CAO J, LIU B, WU Q, et al. Research on the vibration control of micro-vibration using a novel hybrid isolator[J]. Experimental Techniques, 2024: 1–13. doi: 10.1007/S40799-024-00772-3. (查阅网上资料,未找到本条文献卷期页码信息,请确认). [13] SONG Henan, SHAN Xiaobiao, HOU Weijie, et al. A novel piezoelectric-based active-passive vibration isolator for low-frequency vibration system and experimental analysis of vibration isolation performance[J]. Energy, 2023, 278: 127870. doi: 10.1016/j.energy.2023.127870. [14] 徐道临, 张月英, 周加喜, 等. 一种准零刚度隔振器的特性分析与实验研究[J]. 振动与冲击, 2014, 33(11): 208–213. doi: 10.13465/j.cnki.jvs.2014.11.036.XU Daolin, ZHANG Yueying, ZHOU Jiaxi, et al. Characteristic analysis and experimental investigation for a vibration isolator with quasi-zero stiffness[J]. Journal of Vibration and Shock, 2014, 33(11): 208–213. doi: 10.13465/j.cnki.jvs.2014.11.036. [15] ZHENG Zepeng, WANG Shuqing, JIANG Bo, et al. Characteristics of a quasi-zero-stiffness isolator using a double-curved beam as a negative stiffness mechanism[J]. Journal of Ocean University of China, 2024, 23(6): 1409–1422. doi: 10.1007/s11802-024-5762-2. [16] DAI Xiangjun, YE Hangyu, YUAN Tianyu, et al. Strain determination based on strain gauge-guided radial basis function and digital image correlation[J]. Optics and Lasers in Engineering, 2020, 126: 105894. doi: 10.1016/j.optlaseng.2019.105894. [17] 王登攀, 向路, 王露, 等. 基于位移放大的压电致动器设计与仿真[J]. 压电与声光, 2024, 46(3): 376–380. doi: 10.11977/j.issn.1004-2474.2024.03.018.WANG Dengpan, XIANG Lu, WANG Lu, et al. Design and simulation of piezoelectric actuator based on displacement amplification[J]. Piezoelectrics & Acoustooptics, 2024, 46(3): 376–380. doi: 10.11977/j.issn.1004-2474.2024.03.018. [18] 卢可, 宦荣华, 朱位秋, 等. 基于压电叠堆惯性作动器的随机振动控制研究[J]. 力学与实践, 2019, 41(3): 278–282. doi: 10.6052/1000-0879-19-013.LU Ke, HUAN Ronghua, ZHU Weiqiu, et al. Stochastic vibration control based on piezoelectric stack inertial actuator[J]. Mechanics in Engineering, 2019, 41(3): 278–282. doi: 10.6052/1000-0879-19-013. [19] ZHU Wei, CHEN Gangli, and RUI Xiaoting. Modeling of piezoelectric stack actuators considering bonding layers[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(17): 2418–2427. doi: 10.1177/1045389X15575083. [20] 姚晓成, 蒋春燕, 赵程, 等. 压电促动器的研制及其减振效果[J]. 机械工程材料, 2021, 45(6): 89–93. doi: 10.11973/jxgccl202106016.YAO Xiaocheng, JIANG Chunyan, ZHAO Cheng, et al. Fabrication and vibration reduction effect of piezoelectric actuator[J]. Materials for Mechanical Engineering, 2021, 45(6): 89–93. doi: 10.11973/jxgccl202106016. [21] YANG Liu, ZHONG Ruobing, LI Dongjie, et al. A fractional-order Duhem model of rate-dependent hysteresis for piezoelectric actuators[J]. Measurement and Control, 2022, 55(9/10): 974–982. doi: 10.1177/00202940221092140. [22] YANG Liu, CHENG Jiajia, HE He, et al. Cross-medium time-delay active vibration isolation method based on voltage-force hysteresis model[J]. Measurement, 2024, 235: 115027. doi: 10.1016/j.measurement.2024.115027. -
图(13) / 表(3)
计量
- 文章访问数: 22
- HTML全文浏览量: 10
- PDF下载量: 0
- 被引次数: 0
下载:
