Research on Key Technologies of Side-channel Security Protection for Polynomial Multiplication in ML-KEM/Kyber Algorithm
-
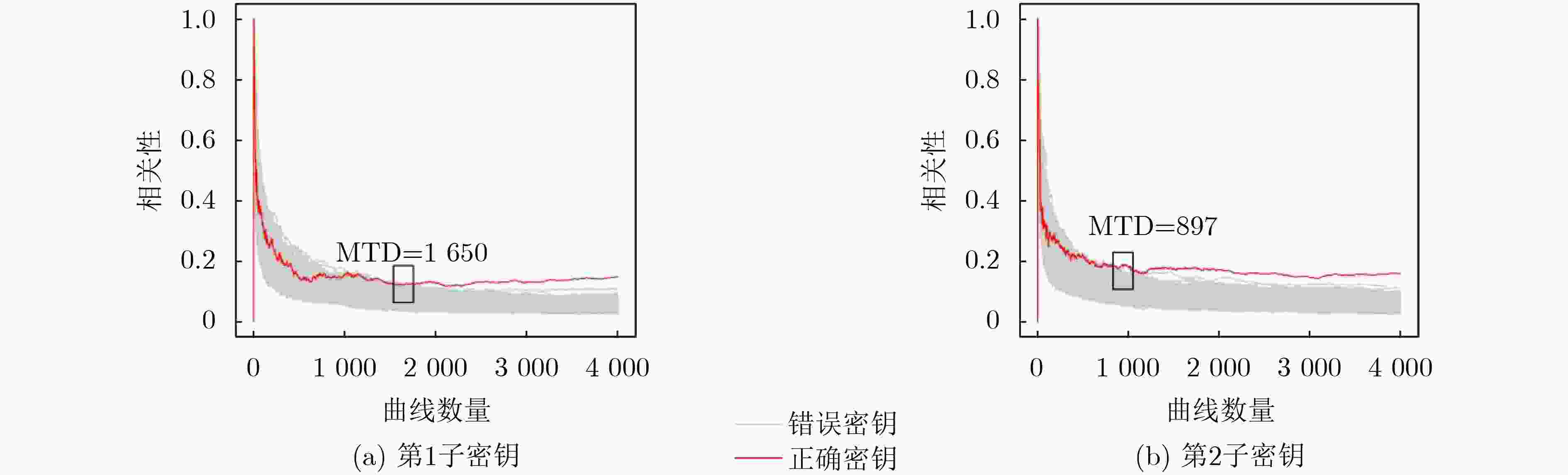
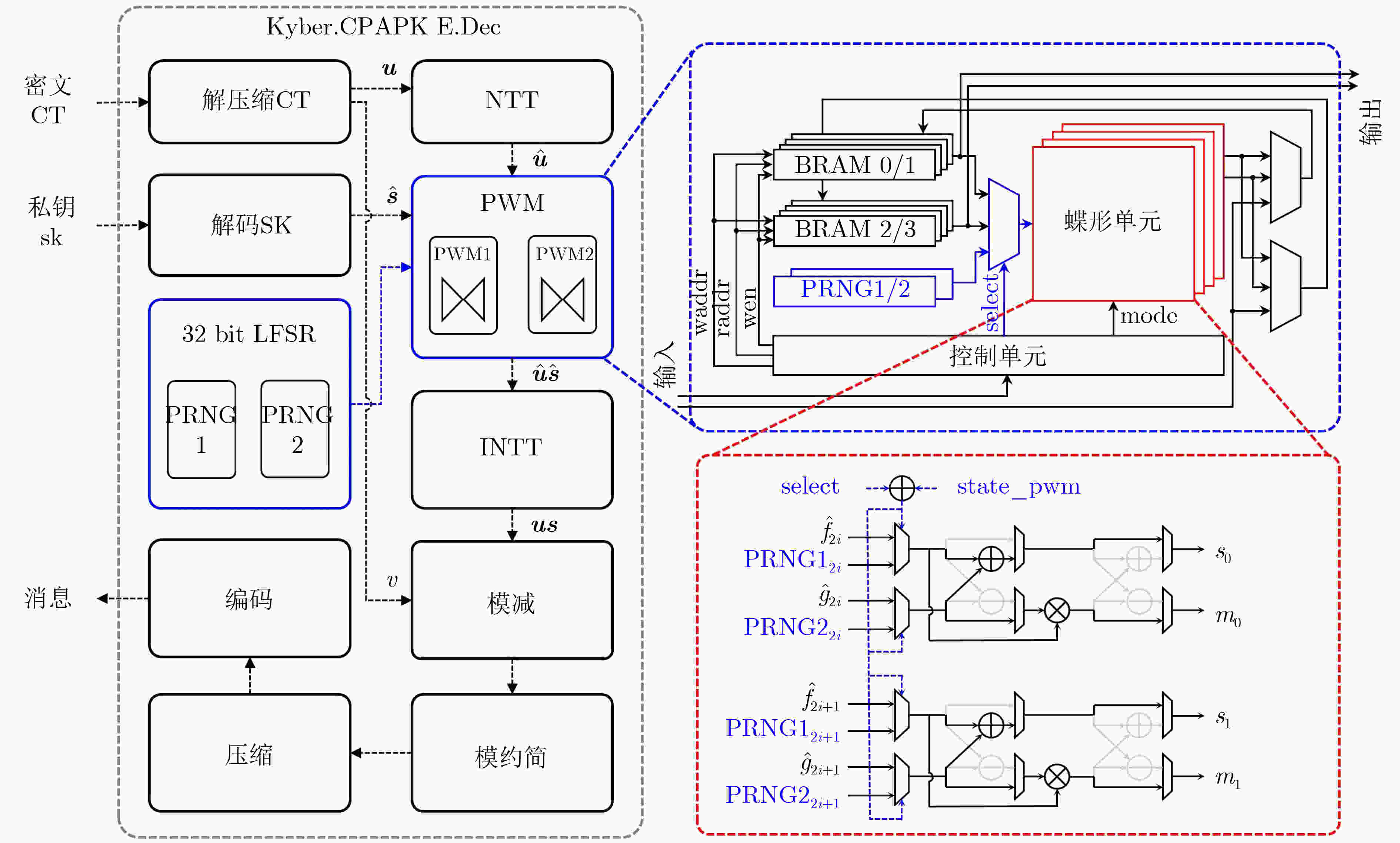
摘要: 后量子密码算法CRYSTALS-Kyber已被美国国家标准与技术研究院(NIST)标准化为唯一的模块化格基密钥封装机制方案 (ML-KEM),以抵御大规模量子计算机的攻击。虽然后量子密码通过数学理论保证了算法的安全性,但在密码实现运算过程中仍面临侧信道威胁。该文针对当前后量子密码算法硬件实现中存在的侧信道泄露风险,提出一种随机伪轮隐藏防护技术,通过动态插入冗余模运算与线性反馈移位寄存器(LFSR)随机调度机制,破坏多项式逐点乘法(PWM)关键操作的时序特征,从而混淆侧信道信息相关性。为了验证其有效性,在Xilinx Spartan-6 FPGA平台对安全增强前后的Kyber解密模块进行实现,并开展基于选择密文的相关功耗分析(CPA)。实验结果表明,防护前攻击者仅需897~1 650条功耗迹线即可恢复Kyber长期密钥;防护后在10 000条迹线下仍无法成功破解,破解密钥所需迹线数量显著提高。同时,相较现有的Kyber防护实现方案,该文的安全增强设计在面积开销上优于其他的隐藏方案。Abstract:
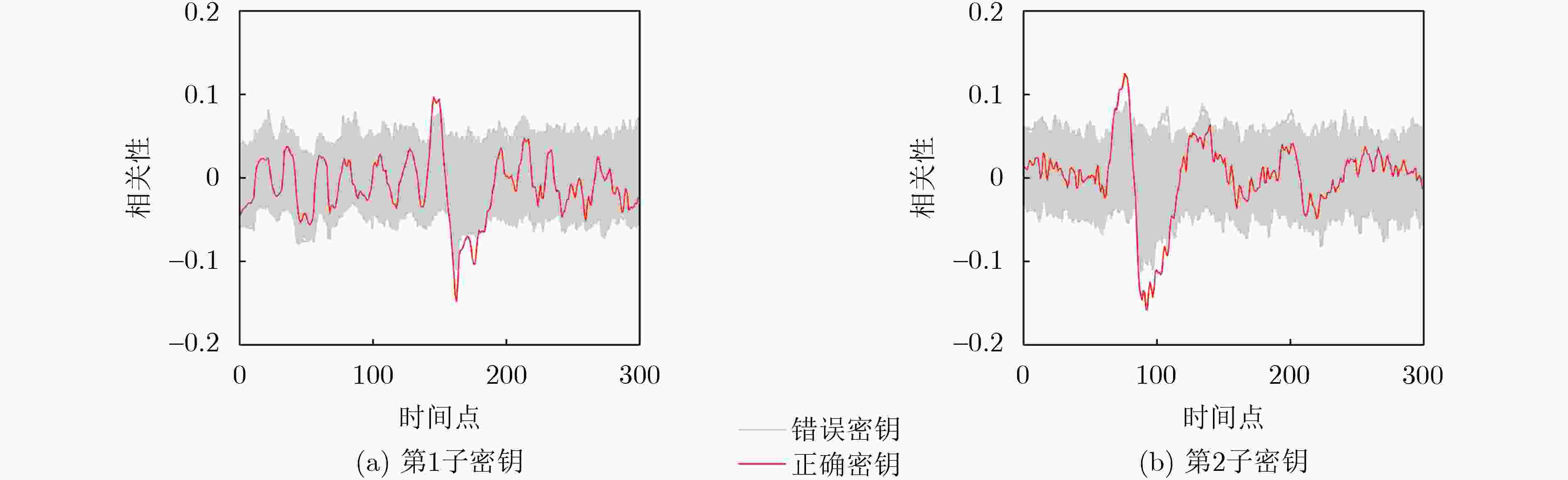
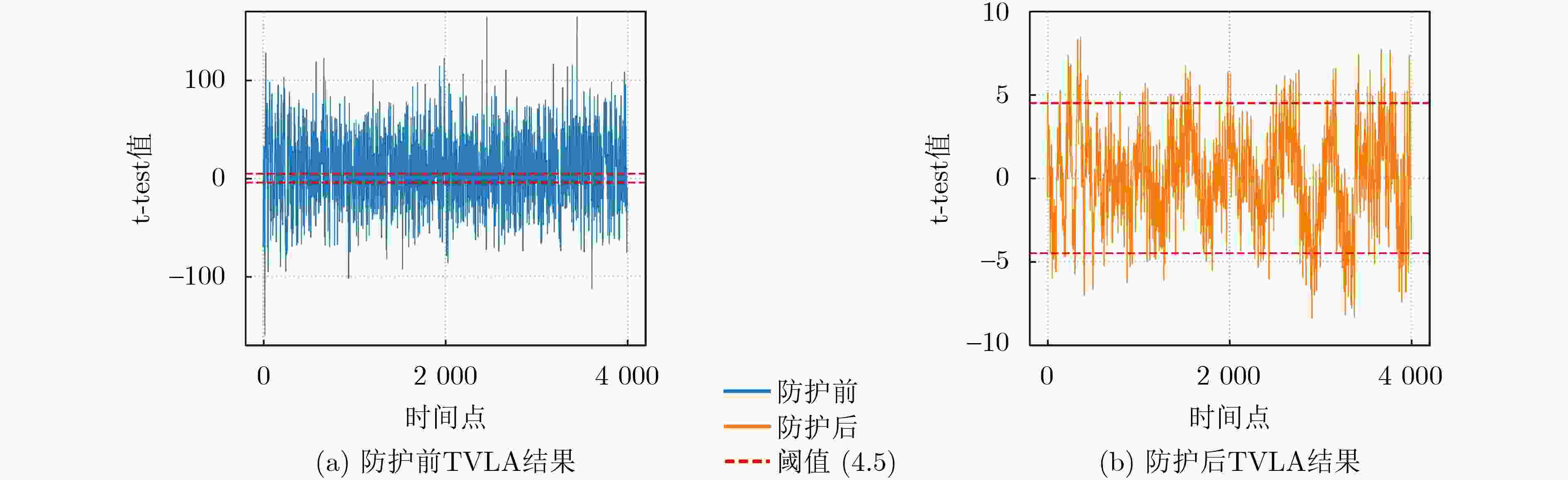
Objective As ML-KEM/Kyber is adopted as a post-quantum key encapsulation mechanism, securing its hardware implementations against Side-Channel Attacks (SCAs) has become critical. Although Kyber offers mathematically proven security, its physical implementations remain susceptible to timing-based side-channel leakage, particularly during Polynomial Point-Wise Multiplication (PWM), a core operation in decryption. Existing countermeasures, such as masking and static hiding, struggle to balance security, resource efficiency, and hardware feasibility. This study proposes a dynamic randomization strategy to disrupt execution timing patterns in PWM, thereby improving side-channel resistance in Kyber hardware designs. Methods A randomized pseudo-round hiding technique is developed to obfuscate the timing profile of PWM computations. The approach incorporates two key mechanisms: (1) dynamic insertion of redundant modular operations (e.g., dummy additions and multiplications), and (2) two-level pseudo-random scheduling based on Linear Feedback Shift Registers (LFSRs). These mechanisms randomize the execution order of PWM operations while reusing existing butterfly units to reduce hardware overhead. The design is implemented on a Xilinx Spartan-6 FPGA and evaluated using Correlation Power Analysis (CPA) and Test Vector Leakage Assessment (TVLA). Results and Discussions Experimental results demonstrate a substantial improvement in side-channel resistance. In unprotected implementations, attackers could recover Kyber’s long-term secret key using as few as 897 to 1,650 power traces. With the proposed countermeasure applied, no successful key recovery occurred even after 10,000 traces, representing more than a 10-fold increase in the number of traces required for key extraction. TVLA results ( Fig. 6 ) confirm the suppression of leakage, with t-test values maintained near the threshold (|t| < 4.5). The resource overhead remains within acceptable bounds: the area-time product increases by 17.99%, requiring only 157 additional Look-Up Tables (LUTs) and 99 Flip-Flops (FFs) compared with the unprotected design. The proposed architecture outperforms existing masking and hiding schemes (Table 3 ), delivering stronger security with lower resource consumption.Conclusions This work presents an efficient and lightweight countermeasure against timing-based SCAs for Kyber hardware implementations. By dynamically randomizing PWM operations, the design significantly enhances side-channel security while maintaining practical resource usage. Future research will focus on optimizing pseudo-round scheduling to reduce latency, extending protection to Kyber’s Fujisaki–Okamoto (FO) transformation modules, and generalizing the method to other Number-Theoretic Transform (NTT)-based lattice cryptographic algorithms such as Dilithium. These developments support the secure and scalable deployment of post-quantum cryptographic systems. -
1 Kyber.CPAPKE.Dec
输入:私钥$ \mathrm{s}\mathrm{k}\in {\mathcal{B}}^{12\cdot k\cdot n/8} $ 输出:密文$ c\in {\mathcal{B}}^{{d}_{u}\cdot k\cdot n/8+{d}_{v}\cdot n/8} $ 输出:消息$ m\in {\mathcal{B}}^{32} $ (1) $ \boldsymbol{u}:={\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}_{q}({\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}}_{{d}_{{\boldsymbol{u}}}}\left(c\right),{d}_{{\boldsymbol{u}}}) $ (2) $ v:={\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}_{q}({\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}}_{{d}_{v}}\left(c+{d}_{{\boldsymbol{u}}}\cdot k\cdot n/8\right),{d}_{v}) $ (3) $ \hat{\boldsymbol{s}}:={\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}}_{12}\left(\mathrm{s}\mathrm{k}\right) $ (4) $ m:={\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}}_{1}\left(\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\right(v-{\mathrm{N}\mathrm{T}\mathrm{T}}^{-1}\left({\hat{\boldsymbol{s}}}^{\mathrm{T}}\circ \mathrm{N}\mathrm{T}\mathrm{T}\left(\boldsymbol{u}\right)\right),1) $ (5) $ \triangleright m :={\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}_{q}\left(v-{\boldsymbol{s}}^{\mathrm{T}}{\boldsymbol{u}},1\right) $ (6) 返回: $ m $ 2 多项式逐点乘法(Point-Wise Multiplication)
输入:$ A\left(x\right)=\left({A}_{0},{A}_{1},\cdots ,{A}_{n-1}\right) $, $ B\left(x\right)=\left({B}_{0},{B}_{1},\cdots ,{B}_{n-1}\right) $
(按位反序排列),$ \zeta (\mathrm{s}.\mathrm{t}.{\zeta }^{n}\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}q) $输出:$ C\left(x\right)=\left({C}_{0},{C}_{1},\cdots ,{C}_{n-1}\right) $(按位反序排列) (1) $ l={\mathrm{l}\mathrm{o}\mathrm{g}}_{2}^{}n $ (2) 循环 $ i $从$ 1 $~$ {n}/{2} $执行 (3) $ w={\zeta }^{\mathrm{b}{\mathrm{r}}_{l-1}\left(i\right)+1}\left(\mathrm{m}\mathrm{o}\mathrm{d}q\right) $ (4) $ {C}_{2i}={A}_{2i+1}\cdot {B}_{2i+1}\cdot w+{A}_{2i}\cdot {B}_{2i}\left(\mathrm{m}\mathrm{o}\mathrm{d}q\right) $ (5) $ {C}_{2i+1}={A}_{2i}\cdot {B}_{2i+1}+{A}_{2i+1}\cdot {B}_{2i}\left(\mathrm{m}\mathrm{o}\mathrm{d}q\right) $ (6) 结束循环 (7) 返回:$ C\left(x\right)=\left({C}_{0},{C}_{1},\cdots ,{C}_{n-1}\right) $ 表 1 Kyber.CPAPKE.Dec详细运算的并行度和时钟周期数[9]
操作 并行度/周期数 Receive $ c={c}_{1}\left|\right|{c}_{2} $ -/713 $ \boldsymbol{u}\left[0\right]=\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\left({c}_{1}\right),\hat{\boldsymbol{u}}\left[0\right]=\mathrm{N}\mathrm{T}\mathrm{T}\left(\boldsymbol{u}\right[0\left]\right) $ 2,4/576 $ {\mathrm{acc}}=\hat{\boldsymbol{u}}\left[0\right]\circ \hat{\boldsymbol{s}}\left[0\right]+0 $ 2/256 $ \boldsymbol{u}\left[1\right]=\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\left({c}_{1}\right),\hat{\boldsymbol{u}}\left[1\right]=\mathrm{N}\mathrm{T}\mathrm{T}\left(\boldsymbol{u}\right[1\left]\right) $ 2,4/576 $ \mathrm{a}\mathrm{c}\mathrm{c}=\hat{\boldsymbol{u}}\left[1\right]\circ \hat{\boldsymbol{s}}\left[1\right]+\mathrm{a}\mathrm{c}\mathrm{c} $ 2/256 $ \boldsymbol{u}\left[2\right]=\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\left({c}_{1}\right),\hat{\boldsymbol{u}}\left[2\right]=\mathrm{N}\mathrm{T}\mathrm{T}\left(\boldsymbol{u}\right[2\left]\right) $ 2,4/576 $ \hat{\boldsymbol{u}}\hat{\boldsymbol{s}}=\hat{\boldsymbol{u}}\left[2\right]\circ \hat{\boldsymbol{s}}\left[2\right]+\mathrm{a}\mathrm{c}\mathrm{c} $ 2/256 $ \boldsymbol{u}\boldsymbol{s}=\mathrm{I}\mathrm{N}\mathrm{T}\mathrm{T}\left(\hat{\boldsymbol{u}}\hat{\boldsymbol{s}}\right) $ 4/448 $ v=\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\left({c}_{2}\right) $ 2/128 $ m=\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\left(\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\right(v-\boldsymbol{u}\boldsymbol{s}\left)\right) $ 2/128 表 2 近期关于对Kyber侧信道攻击的研究
表 3 不同防护方案下 Kyber解封装算法的 FPGA 实现性能与安全性比较
文献 防护 k LUTs FFs Slice DSP BRAM ENS1 Cycle
($ \times $103)频率
(MHz)ATP 2
(ENS$ \times \mathrm{m}\mathrm{s} $)MTD 本文 无防护 3 7 444 4 218 2 526 2 11 4 926 10.0 206 239.1 897 本文 随机伪轮 3 7 601 4 317 2 481 2 11 4 881 11.9 206 282 >10k [10] 混合掩码 3 9 905 6 695 3 334 2 11 5 744 10.0 206 278.8 >10k [17] 复制+
时钟随机化3 14 341 9 190 4 734 3 $ \ge $2 6 $ \ge $6 134 10.0 $ \le $206 $ \ge $297.8 - [16] 仅掩码 2 143 112 - 81 746 60 294 146 546 126.6 100 186$ \times $103 - [16] 掩码+隐藏 2 152 860 - 92 977 76 489.5 198 477 137.7 100 273$ \times $103 >50k [18] 随机延迟
+混淆2 7 151 3 730 2 260 3 2 5.5 3 560 57.2 258 789.3 - 1.等效Slice数ENS (Equivalent Number of Slices)=Slice+100×DSP+200×BRAM[19]
2.面积时间积ATP(Area-Time Product) = ENS×时间(ms)=ENS×Cycle×1/频率×103
3.Slice数量使用0.25×LUTs+0.125×FFs进行近似计算[19] -
[1] SHOR P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Review, 1999, 41(2): 303–332. doi: 10.1137/S0036144598347011. [2] National Institute of Standards and Technology. FIPS 203-2024 Module-lattice-based key-encapsulation mechanism standard[S]. Gaithersburg: U. S. Department of Commerce, 2024. doi: 10.6028/NIST.FIPS.203. [3] PRIMAS R, PESSL P, and MANGARD S. Single-trace side-channel attacks on masked lattice-based encryption[C]. 19th International Conference on Cryptographic Hardware and Embedded Systems, Taipei, China, 2017: 513–533. doi: 10.1007/978-3-319-66787-4_25. [4] KARLOV A and DE GUERTECHIN N L D. Power analysis attack on Kyber[EB/OL]. https://eprint.iacr.org/2021/1311, 2021. [5] HAMBURG M, HERMELINK J, PRIMAS R, et al. Chosen ciphertext k-trace attacks on masked CCA2 secure Kyber[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(4): 88–113. doi: 10.46586/tches.v2021.i4.88-113. [6] RAVI P, JAP D, BHASIN S, et al. Machine learning based blind side-channel attacks on PQC-based KEMs - a case study of Kyber KEM[C]. 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, USA, 2023: 1–7. doi: 10.1109/ICCAD57390.2023.10323721. [7] 王亚琦, 黄帆, 段晓林, 等. 对Kyber算法的二阶侧信道攻击: 针对掩码哈希函数(英文)[J]. 密码学报(中英文), 2024, 11(6): 1415–1436. doi: 10.13868/j.cnki.jcr.000745.WANG Yaqi, HUANG Fan, DUAN Xiaolin, et al. Second-order side-channel attacks on Kyber: Targeting the masked hash function[J]. Journal of Cryptologic Research, 2024, 11(6): 1415–1436. doi: 10.13868/j.cnki.jcr.000745. [8] ZHAO Yifan, XIE Ruiqi, XIN Guozhu, et al. A high-performance domain-specific processor with matrix extension of RISC-V for module-LWE applications[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(7): 2871–2884. doi: 10.1109/TCSI.2022.3162593. [9] XING Yufei and LI Shuguo. A compact hardware implementation of CCA-secure key exchange mechanism CRYSTALS-KYBER on FPGA[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2020(2): 328–356. doi: 10.46586/tches.v2021.i2.328-356. [10] ZHAO Yiqiang, PAN Shijian, MA Haocheng, et al. Side channel security oriented evaluation and protection on hardware implementations of Kyber[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(12): 5025–5035. doi: 10.1109/TCSI.2023.3288600. [11] MA Haocheng, PAN Shijian, GAO Ya, et al. Vulnerable PQC against side channel analysis - a case study on Kyber[C]. 2022 Asian Hardware Oriented Security and Trust Symposium (AsianHOST), Singapore, Singapore, 2022: 1–6. doi: 10.1109/AsianHOST56390.2022.10022165. [12] WANG Jian, CAO Weiqiong, CHEN Hua, et al. Blink: Breaking parallel implementation of crystals-Kyber with side-channel attack[C]. 2024 IEEE 42nd International Conference on Computer Design (ICCD), Milan, Italy, 2024: 105–113. doi: 10.1109/ICCD63220.2024.00026. [13] JI Yanning, WANG Ruize, NGO K, et al. A side-channel attack on a hardware implementation of CRYSTALS-Kyber[C]. 2023 IEEE European Test Symposium (ETS), Venezia, Italy, 2023: 1–5. doi: 10.1109/ETS56758.2023.10174000. [14] RODRIGUEZ R C, BRUGUIER F, VALEA E, et al. Correlation electromagnetic analysis on an FPGA implementation of CRYSTALS-Kyber[C]. 2023 18th Conference on Ph. D Research in Microelectronics and Electronics (PRIME), Valencia, Spain, 2023: 217–220. doi: 10.1109/PRIME58259.2023.10161764. [15] 胡伟, 袁超绚, 郑健, 等. 一种针对格基后量子密码的能量侧信道分析框架[J]. 电子与信息学报, 2023, 45(9): 3210–3217. doi: 10.11999/JEIT230267.HU Wei, YUAN Chaoxuan, ZHENG Jian, et al. A power side-channel attack framework for lattice-based post quantum cryptography[J]. Journal of Electronics & Information Technology, 2023, 45(9): 3210–3217. doi: 10.11999/JEIT230267. [16] KAMUCHEKA T, NELSON A, ANDREWS D, et al. A masked pure-hardware implementation of Kyber cryptographic algorithm[C]. 2022 International Conference on Field-Programmable Technology (ICFPT), Hong Kong, China, 2022: 1. doi: 10.1109/ICFPT56656.2022.9974404. [17] MORAITIS M, JI Yanning, BRISFORS M, et al. Securing CRYSTALS-Kyber in FPGA using duplication and clock randomization[J]. IEEE Design & Test, 2024, 41(5): 7–16. doi: 10.1109/MDAT.2023.3298805. [18] JATI A, GUPTA N, CHATTOPADHYAY A, et al. A configurable CRYSTALS-Kyber hardware implementation with side-channel protection[J]. ACM Transactions on Embedded Computing Systems, 2024, 23(2): 33. doi: 10.1145/3587037. [19] LI Minghao, TIAN Jing, HU Xiao, et al. Reconfigurable and high-efficiency polynomial multiplication accelerator for CRYSTALS-Kyber[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2023, 42(8): 2540–2551. doi: 10.1109/TCAD.2022.3230359. -





 下载:
下载:


 下载:
下载:
