基于符号级预编码的雷达通信一体化恒模波形设计算法研究

翟怡昊; 赵宏宇; 牛凤梁; 李静妍

doi:10.11999/JEIT250288

基于符号级预编码的雷达通信一体化恒模波形设计算法研究

doi: 10.11999/JEIT250288 cstr: 32379.14.JEIT250288

中国人民解放军63892部队洛阳 471032

详细信息

作者简介:
翟怡昊：男，研究实习员，研究方向为雷达对抗半实物仿真、雷达波形设计等

赵宏宇：男，助理研究员，研究方向为雷达对抗半实物仿真

牛凤梁：男，助理研究员，研究方向为雷达对抗半实物仿真

李静妍：女，研究实习员，研究方向为雷达对抗半实物仿真

通讯作者:
翟怡昊　yihao_zhai@163.com

中图分类号: TN929.5
计量
- 文章访问数: 17
- HTML全文浏览量: 13
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2025-04-17
- 修回日期: 2025-09-15
- 网络出版日期: 2025-09-22

Constant-Modulus Waveform Design for SLP-Based DFRC Systems

Unit 63892 of PLA, Luoyang 471032, China

摘要

摘要: 针对干扰环境下双功能雷达通信一体化(DFRC)系统感知性能下降的问题，该文提出一种发射波形和接收滤波器联合设计来提高系统性能。首先，为了保证系统通信性能，利用符号级预编码(SLP)设计通信建设性干扰(CI)约束。基于此，构建以最大化雷达接收回波信干噪比(SINR)为优化准则，以通信CI为约束条件的优化问题。此外，引入恒模约束避免发射波形的非线性失真。针对发射波形和接收滤波器联合优化问题，该文提出一种基于交替优化的迭代算法。当固定发射波形时，子问题可转换为最小方差无失真响应(MVDR)问题。当固定接收滤波器时，将通信CI约束转化为惩罚项纳入子问题目标函数中，从而将原问题转化为黎曼复圆流形中的无约束问题，利用黎曼共轭梯度法进行有效求解。仿真结果表明所提方法能够以较低的时间成本有效提高系统在干扰环境中的感知和通信性能。
- 雷达通信一体化 /
- 符号级预编码 /
- 建设性干扰 /
- 流形优化
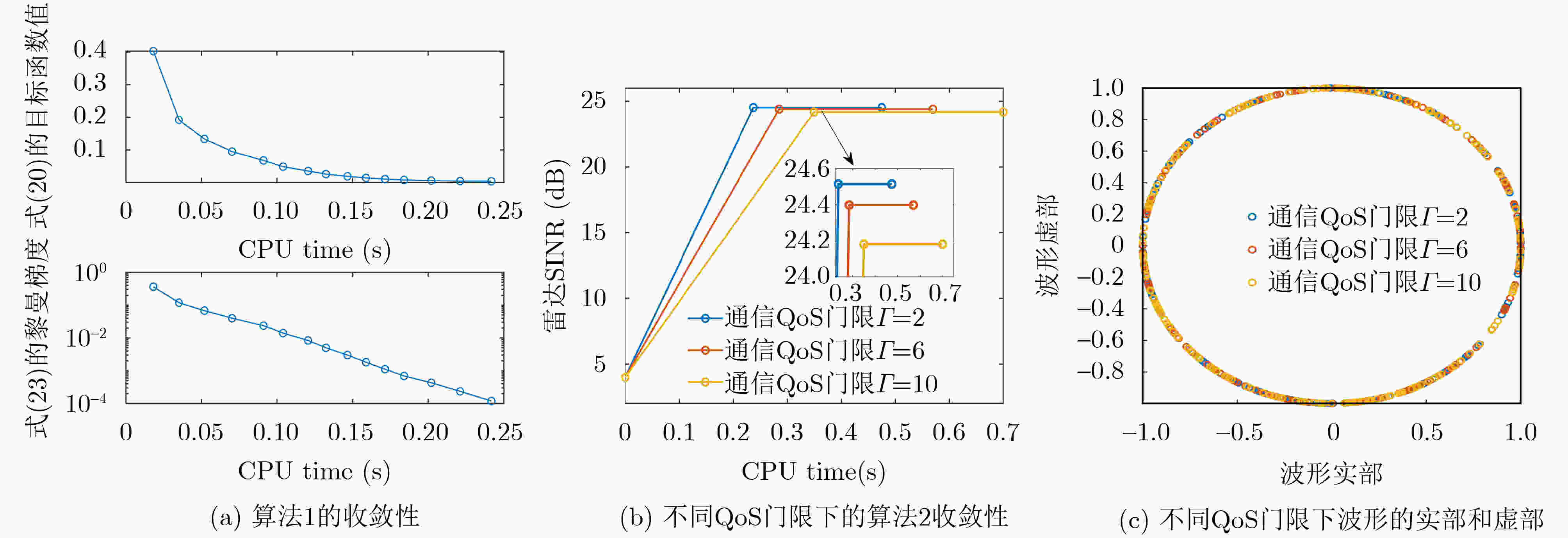
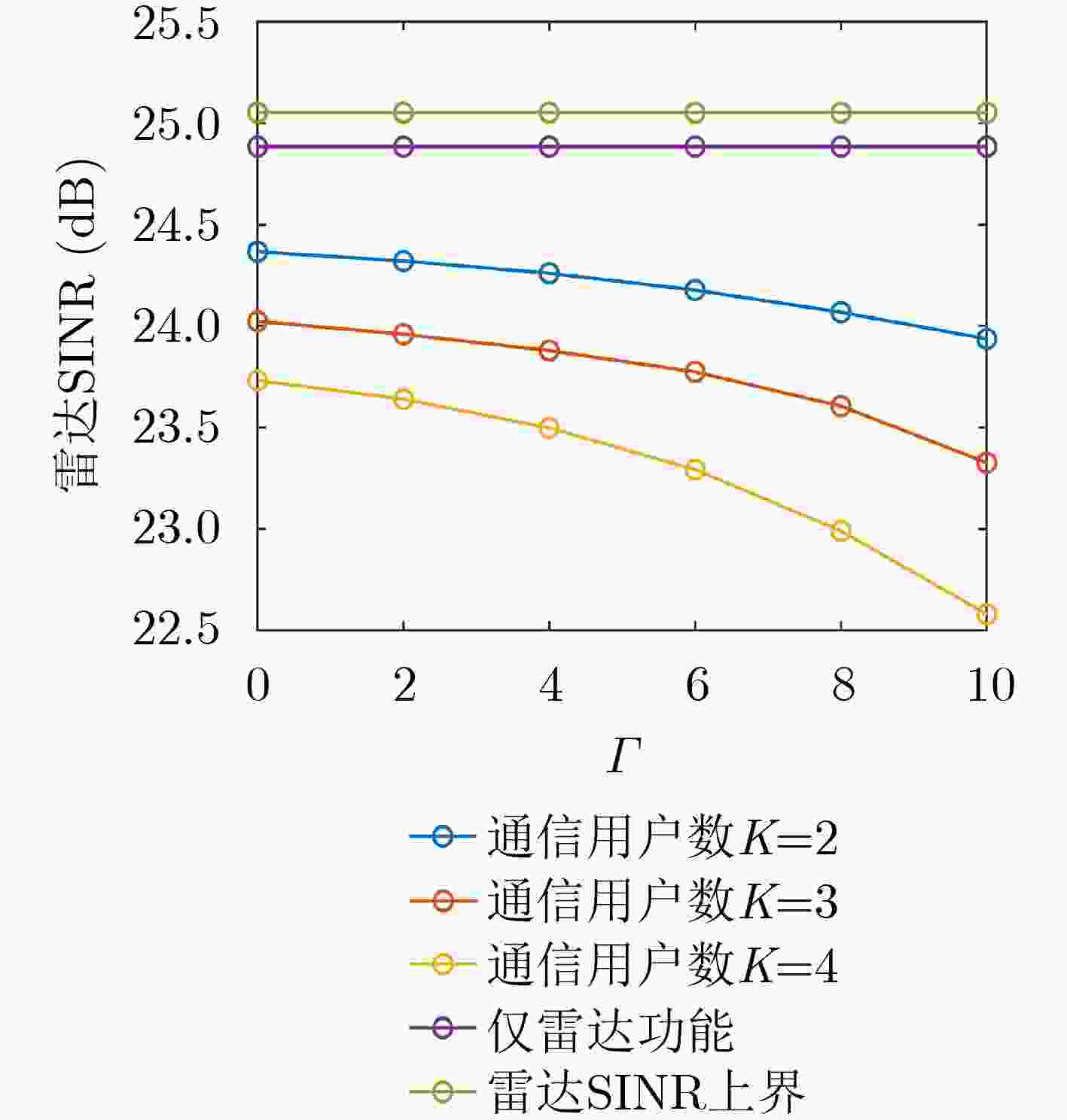
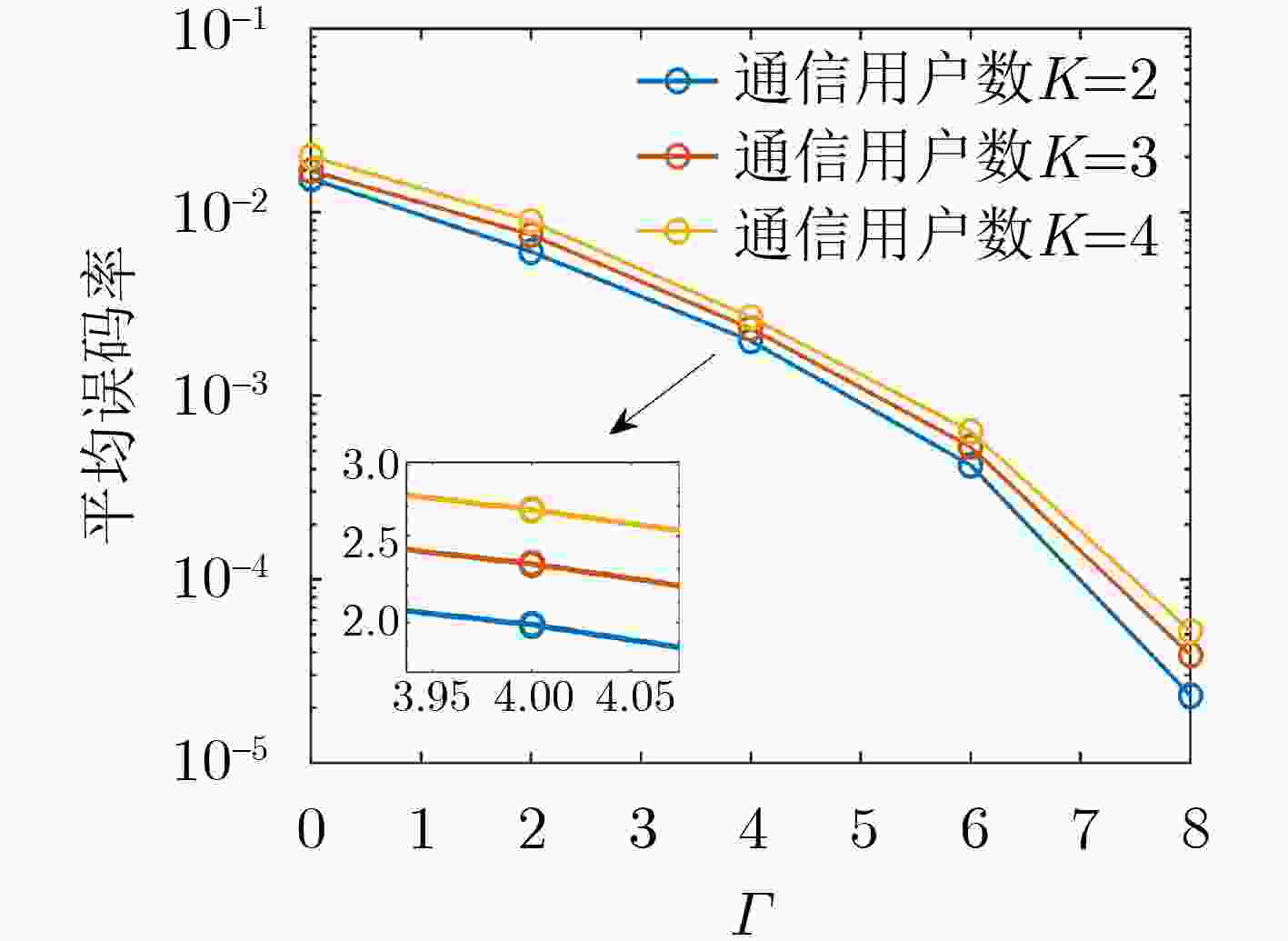
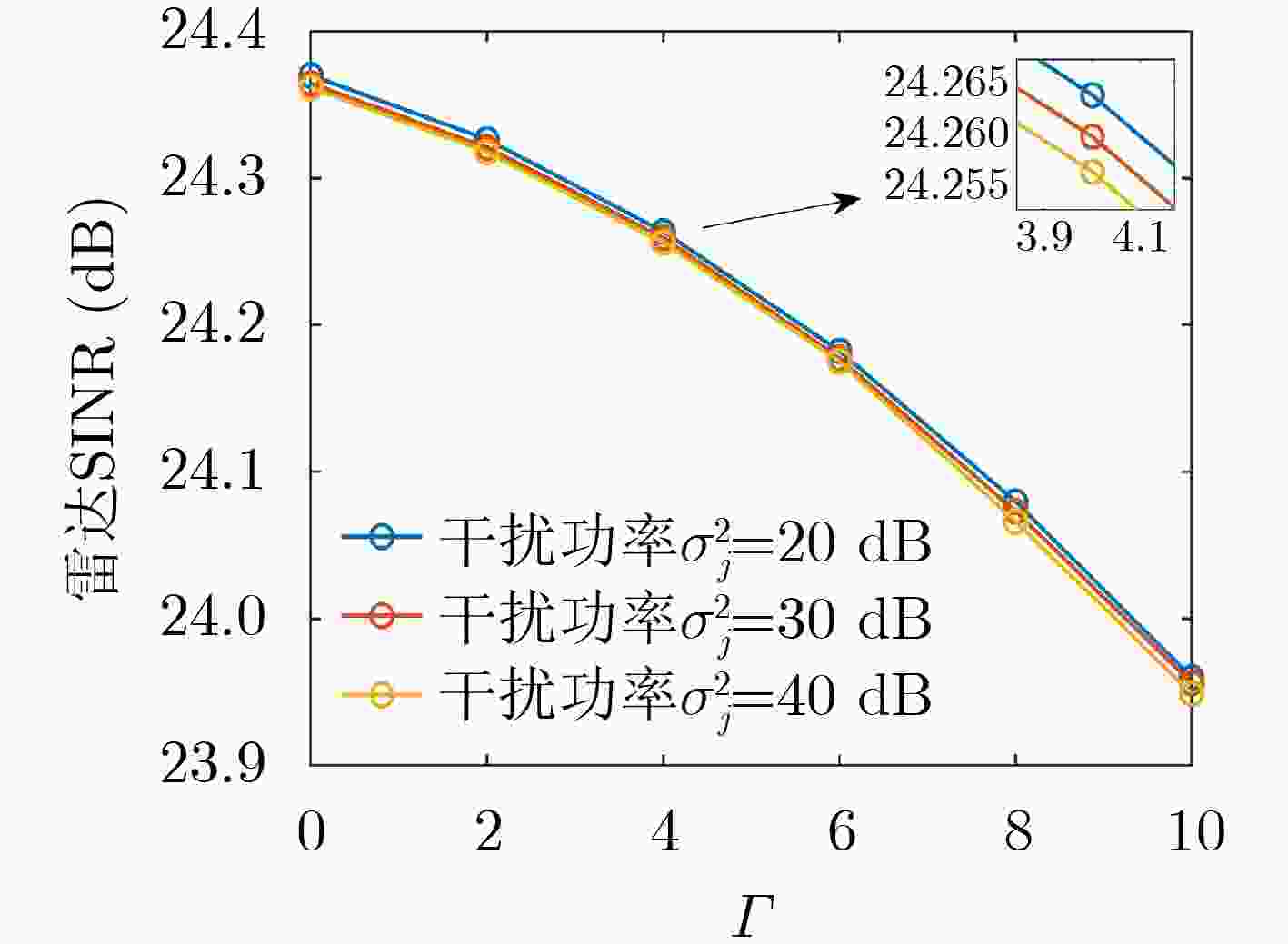
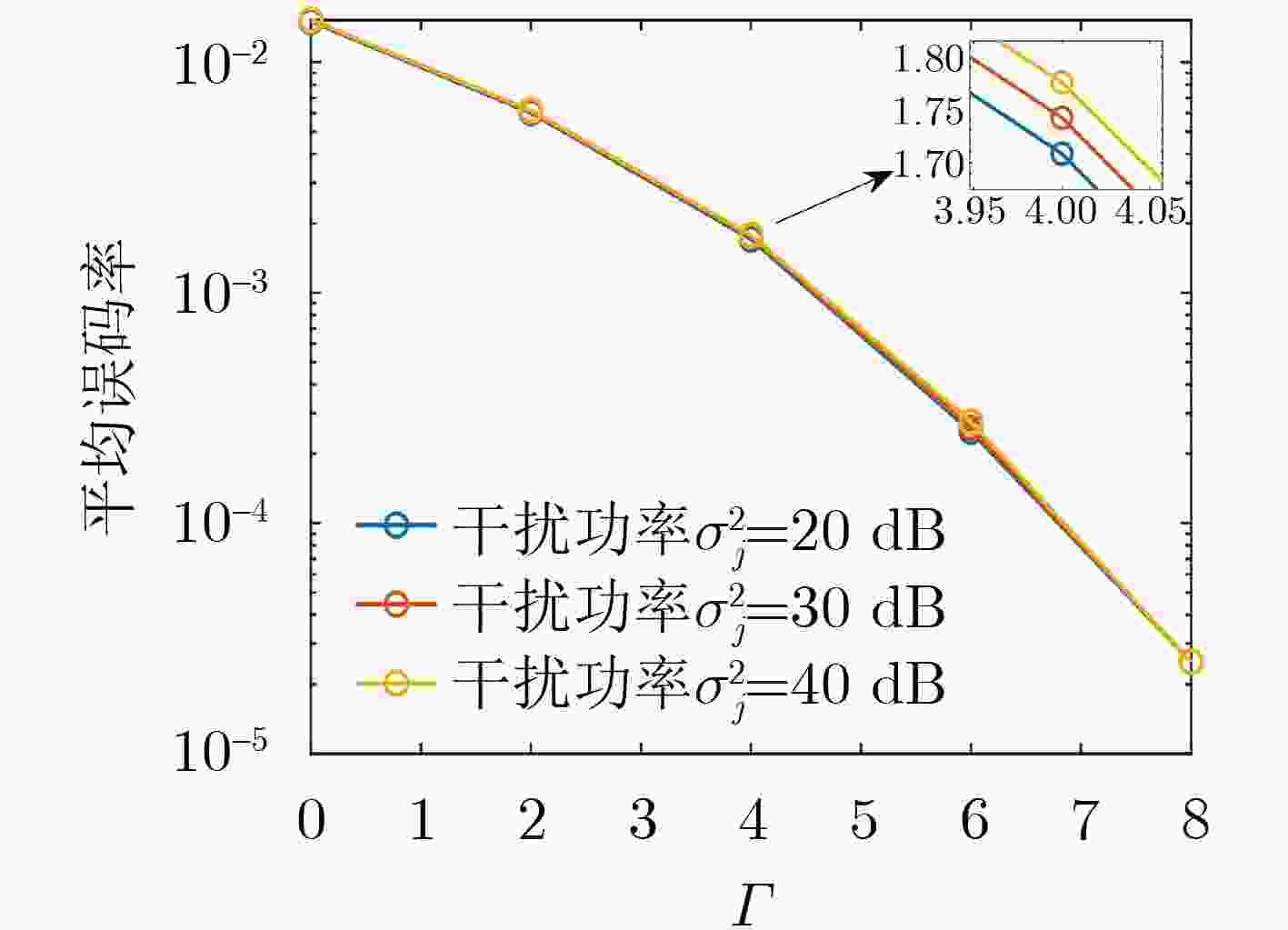
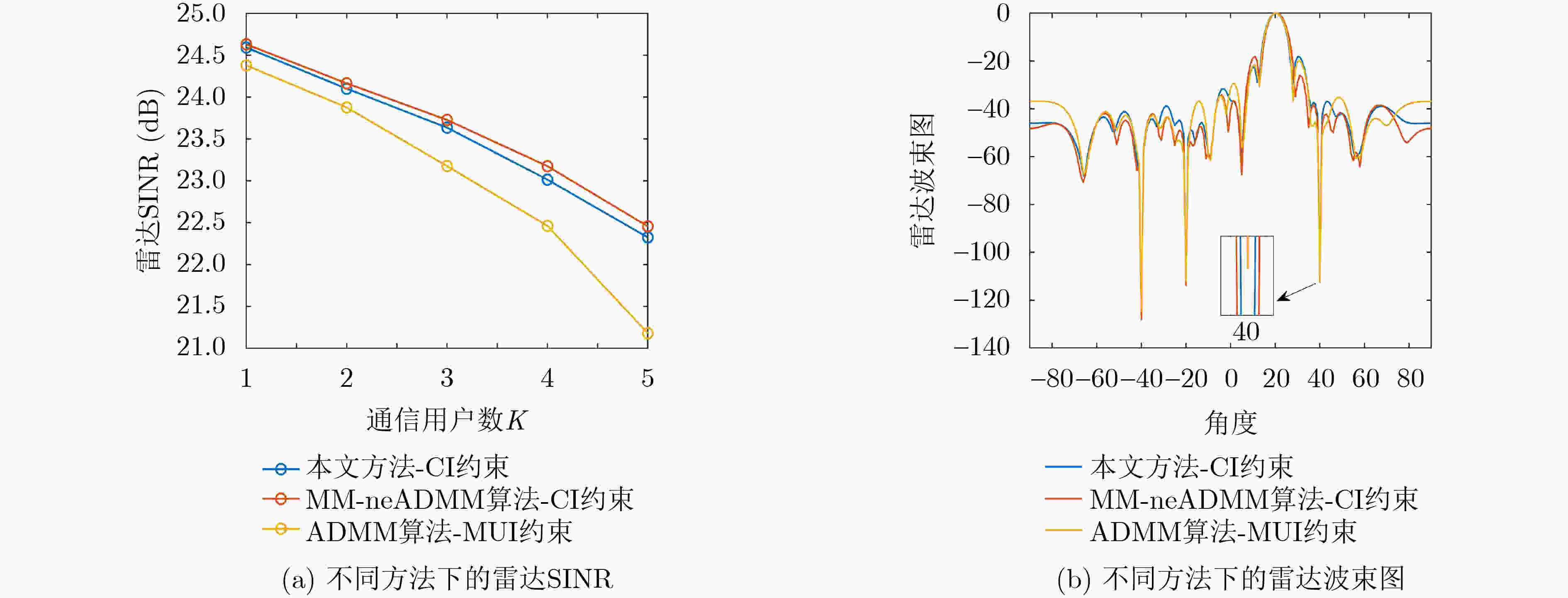
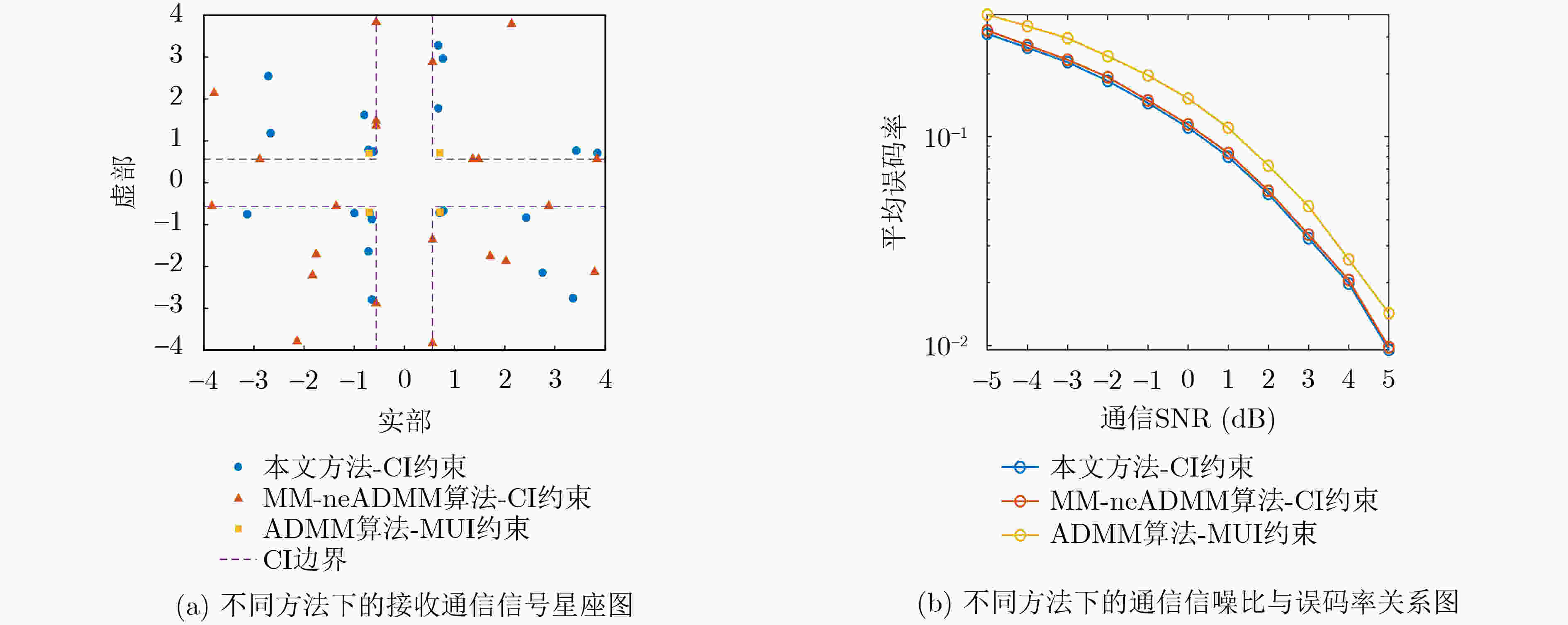
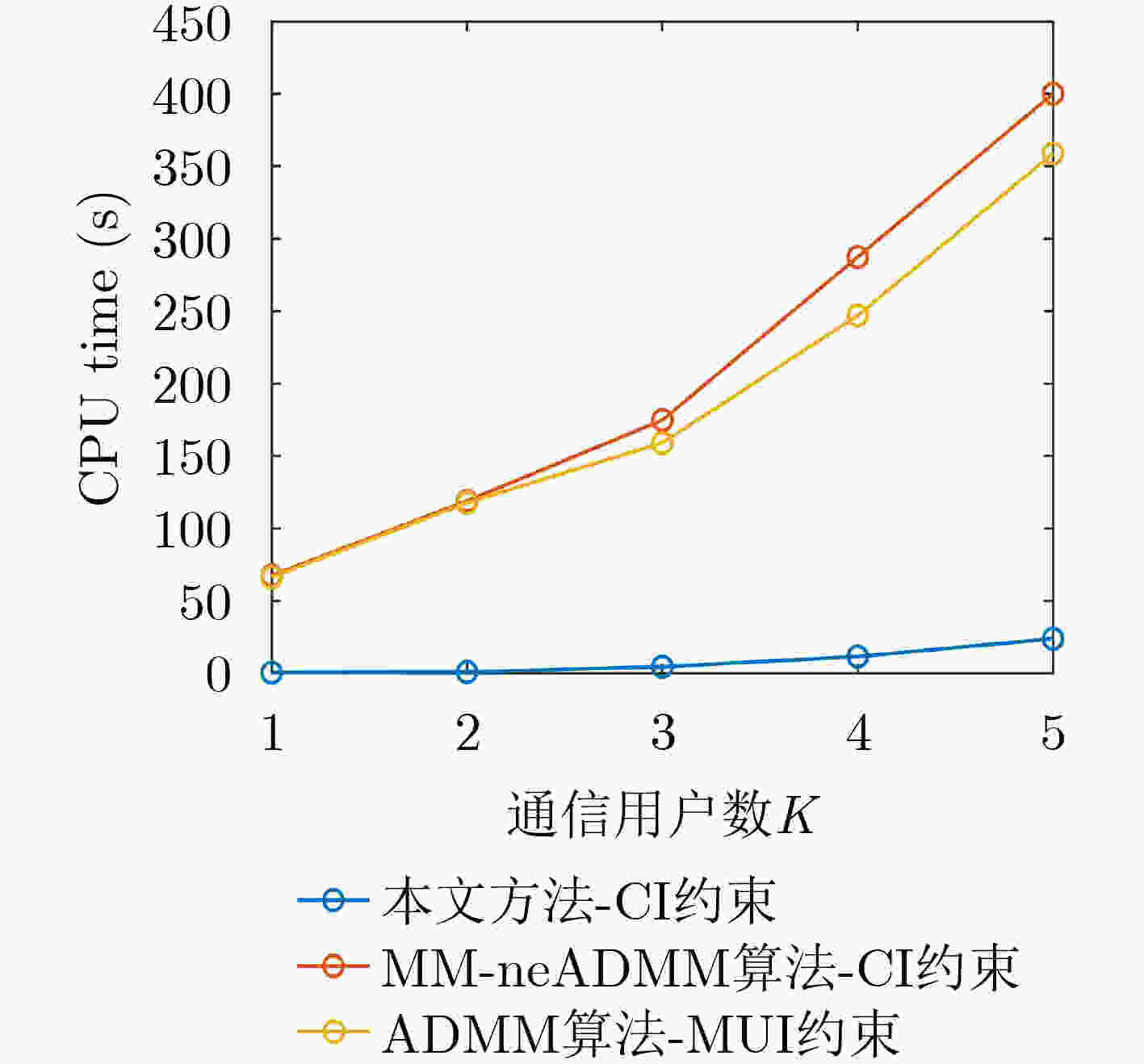
Abstract: Objective Dual-Function Radar–Communication (DFRC) Integration is a promising technology for addressing spectrum congestion. The key challenge in DFRC lies in designing a dual-functional waveform that simultaneously supports both radar sensing and communication. Previous research has primarily focused on designing transmit waveforms under Multi-User Interference (MUI) energy constraints. However, not all MUI energy is detrimental in DFRC systems. Symbol-Level Precoding (SLP) can exploit symbol information to transform harmful MUI into constructive components, thereby enhancing communication Quality of Service (QoS). To further leverage the advantages of SLP in mitigating MUI energy and to improve target detection in cluttered environments, this work studies the joint design of transmit waveforms and receive filters for DFRC systems. Methods The analytical expression of the radar output Signal-to-Interference-plus-Noise Ratio (SINR) is first derived. To guarantee communication performance, Constructive Interference (CI) constraints are formulated using SLP. Based on these, a joint optimization problem is established, where maximizing the radar output SINR serves as the objective function and the communication CI constraints are imposed. A constant-modulus condition is also enforced to prevent nonlinear distortion of the transmitted waveform. To address the non-convex nature of the joint optimization problem, an iterative algorithm based on cyclic optimization is proposed. For a fixed transmitted waveform, the subproblem reduces to a Minimum Variance Distortionless Response (MVDR) problem. For a fixed filter, the communication CI constraints are incorporated into the objective function of the subproblem as a penalty term, leading to an unconstrained problem whose feasible region is a Riemannian complex manifold. This problem is then solved efficiently using the Riemannian Conjugate Gradient (RCG) method. Results and Discussions As shown in (Fig 3): (a) the proposed method converges within a short time, and (b) the designed waveform satisfies the constant-modulus constraint. (Figs. 4 and 5) analyze the effect of the number of communication users and the communication QoS threshold on radar output SINR and communication SER, confirming the trade-off between radar sensing and communication performance. (Figs. 6 and 7) illustrate the effect of interference power and communication QoS threshold on radar output SINR and communication SER, demonstrating the robustness of the proposed method under different interference power levels. When communication QoS requirements are fixed, the radar output SINR and communication SER performance of the three compared cases remain similar. (Fig. 8(a)) shows the radar output SINR versus the number of communication users. The results indicate that the proposed CI-based waveform consistently outperforms the conventional MUI-based waveform in radar output SINR. Moreover, the two CI-based methods achieve almost identical SINR performance. (Fig. 8(b)) presents the radar received beampatterns, where it can be observed that the deep nulls formed in the interference directions are deeper than those obtained with the conventional MUI-based method. This confirms that the proposed method effectively suppresses signal-dependent interference. (Fig. 9(a)) presents the received communication constellations. The synthesized communication signals of the CI-based methods are more sparsely distributed and exhibit higher power compared with the conventional MUI-based method. (Fig. 9(b)) further evaluates the communication SER performance, showing that the proposed method achieves a lower SER. This improvement arises because the communication CI constraints transform harmful MUI into useful signal energy, thereby enhancing communication QoS. (Fig. 10) presents the relationship between CPU time and the number of communication users. The results show that CPU time increases for all methods as the number of communication users grows, since a larger number of users reduces the feasibility region. Nevertheless, the proposed method demonstrates significantly higher computational efficiency compared with existing approaches. Conclusions This paper investigates the joint design of transmit waveforms and receive filters for MIMO-DFRC systems. A joint optimization problem is formulated to maximize radar output SINR under constant-modulus and communication CI constraints. To solve the resulting non-convex problem, an alternating optimization algorithm based on the RCG method is developed. Simulation results demonstrate that CI-based methods outperform the MUI-based ADMM method in both radar sensing performance and communication QoS. In addition, the proposed method achieves faster convergence compared with the MM-neADMM method, with only a minor loss in radar sensing performance.
- Dual-Functional Radar–Communication (DFRC) /
- Symbol-Level Precoding (SLP) /
- Constructive Interference (CI) /
- Manifold optimization

HTML全文

图 1 基于MIMO的DFRC系统

下载: 全尺寸图片幻灯片

图 2 QPSK星座图的CI构造区域

下载: 全尺寸图片幻灯片

图 3 所提算法收敛性分析

下载: 全尺寸图片幻灯片

图 4 不同通信用户数下雷达SINR随QoS门限的变化曲线

下载: 全尺寸图片幻灯片

图 5 不同通信用户数下平均误码率随QoS门限的变化曲线

下载: 全尺寸图片幻灯片

图 6 不同干扰功率下雷达SINR随QoS门限的变化曲线

下载: 全尺寸图片幻灯片

图 7 不同干扰功率下平均误码率随QoS门限的变化曲线

下载: 全尺寸图片幻灯片

图 8 不同方法下的雷达性能分析

下载: 全尺寸图片幻灯片

图 9 不同方法下的通信性能分析

下载: 全尺寸图片幻灯片

图 10 不同方法下的通信用户数与CPU运行时间关系图

下载: 全尺寸图片幻灯片

1 求解问题(15)的EPM-RCG算法流程

输入：$ {{\boldsymbol{h}}_k} $, ${{\boldsymbol{w}}^{{\mathrm{opt}}}}$, ${\boldsymbol{ A}}\left( {{\theta _0}} \right) $, $ {\boldsymbol{A}}\left( {{\theta _j}} \right) $, $ {\varGamma _k} $
输出：发射波形$ {\boldsymbol{x}} $
初始化 $ {\mu _0} $, $ {\rho _0} $, $ {\theta _u},{\theta _\varepsilon } \in \left( {0,1} \right) $, $ {\theta _\rho } > 1 $, $ {\mu _{\min }} $, $ {\varepsilon _{\min }} $, ${d_{\min }}$
1 While $ {\delta _{opt}} > {d_{\min }},{\varepsilon _{p + 1}} > {\varepsilon _{\min }},{\mu _{p + 1}} > {\mu _{\min }} $
2 　While $ {\text{grad }}f\left( x \right) > {\varepsilon _p} $
3 　　根据式(24)计算欧式梯度$ \nabla f\left( {\boldsymbol{x}} \right) $
4 　　根据式(23)计算黎曼梯度$ {\text{grad }}f\left({\boldsymbol{ x}} \right) $
5 　　根据式(25)计算梯度下降方向$ {{\boldsymbol{\eta}} _m} $
6 　　根据式(26)更新$ {{\boldsymbol{x}}_{m + 1}} $,$m = m + 1$
7 　End While
8 $ {\varepsilon _{p + 1}} = \max \left( {{\varepsilon _{\min }},{\theta _\varepsilon }{\varepsilon _p}} \right) $
9 $ {\mu _{p + 1}} = \max \left( {{\mu _{\min }},{\theta _u}{\mu _p}} \right) $
10 if $ \max \left( {0,{g_{i}}\left( {{{{\boldsymbol{x}}}_{{p} + 1}}} \right)} \right) > {\mu _{p}} $ then
11 $ {\rho _{{p} + 1}} = {\theta _\rho }{\rho _{p}} $
12 else
13 $ {\rho _{{p} + 1}} = {\rho _{p}} $
14 End if
15 ${\delta _{{\mathrm{opt}}}} = {\left\\| {{{{\boldsymbol{x}}}_{{p} + 1}} - {{{\boldsymbol{x}}}_{p}}} \right\\|_2},{p} = {p} + 1$
16 End while

下载: 导出CSV

2 求解问题(11)的交替优化算法流程

输入：$ {{\boldsymbol{h}}_k} $, $ {\boldsymbol{A}}\left( {{\theta _0}} \right) $,$ {\boldsymbol{A}}\left( {{\theta _j}} \right) $, $ {\varGamma _k} $
输出：发射波形$ {\boldsymbol{x}} $，波器权向量$ {\boldsymbol{w}} $
初始化 $ {\mu _0} $, $ {\rho _0} $, $ {\theta _u},{\theta _\varepsilon } \in \left( {0,1} \right) $, $ {\theta _\rho } > 1 $,$ {\mu _{\min }} $,$ {\varepsilon _{\min }} $, ${d_{\min }}$
1 repeat
2 　根据式(13)计算滤波器权向量$ {{\boldsymbol{w}}^{\left( c \right)}} $
3 　根据算法2优化发射波形$ {{\boldsymbol{x}}^{\left( c \right)}} $
4 　更新$c = c + 1$
5 　until 满足式(33)

下载: 导出CSV

表 1 波形设计算法计算复杂度对比

文献	复杂度	参数
文献[19]	$ \mathcal{O}\left( {{M}_{\rm R}^3{{N}^3} + {{N}_D}{{N}_A}\left( {2{K} + 3} \right){M}_{\rm T}^2{{N}^2}} \right) $	$ {M_{\rm T}},{M_{\rm R}} $：发射/接收天线数
文献[22]	$ \mathcal{O}\left( {{{N}_{D}}\sqrt {4{K} + {{M}_{T}}{N}} {{N}^2}{{M}_{T}}\left( {2{K} + {{M}_{T}} + 2{NM}_{T}^2} \right)} \right) $	$ K $：通信用户数，$ N $：码元长度
本文	$ \mathcal{O}\left( {{{N}_{{RCG}}}{M}_{T}^2{{N}^2} + {M}_{R}^3{{N}^3}} \right) $	$ {{N}_{D}},{{N}_{A}},{{N}_{{RCG}}} $：迭代次数

下载: 导出CSV

参考文献(24)

[1]	LI Jiapeng, SHAO Xiaodan, CHEN Feng, et al. Networked integrated sensing and communications for 6G wireless systems[J]. IEEE Internet of Things Journal, 2024, 11(17): 29062–29075. doi: 10.1109/JIOT.2024.3406598.
[2]	LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. doi: 10.1109/JSAC.2022.3156632.
[3]	FENG Xiang, ZHAO Zhongqing, ZHAO Yufei, et al. OFDM-based waveform design for MIMO DFRC systems with reduced range sidelobes: A majorization-minimization approach[J]. IEEE Transactions on Vehicular Technology, 2025, 74(3): 4582–4595. doi: 10.1109/TVT.2024.3498953.
[4]	HUANG Yixuan, HU Su, MA Shiyong, et al. Designing low-PAPR waveform for OFDM-based RadCom systems[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 6979–6993. doi: 10.1109/TWC.2022.3153606.
[5]	XU Zhaoyi and PETROPULU A. A bandwidth efficient dual-function radar communication system based on a MIMO radar using OFDM waveforms[J]. IEEE Transactions on Signal Processing, 2023, 71: 401–416. doi: 10.1109/TSP.2023.3241779.
[6]	HASSANIEN A, AMIN M G, ZHANG Y D, et al. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2168–2181. doi: 10.1109/TSP.2015.2505667.
[7]	ELBIR A M, CELIK A, ELTAWIL A M, et al. Index modulation for integrated sensing and communications: A signal processing perspective[J]. IEEE Signal Processing Magazine, 2024, 41(5): 44–55. doi: 10.1109/MSP.2024.3444195.
[8]	LIU Fan, ZHOU Longfei, MASOUROS C, et al. Toward dual-functional radar-communication systems: Optimal waveform design[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4264–4279. doi: 10.1109/TSP.2018.2847648.
[9]	LIU Fan, MASOUROS C, LI Ang, et al. MU-MIMO communications with MIMO radar: From co-existence to joint transmission[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2755–2770. doi: 10.1109/TWC.2018.2803045.
[10]	LIU Xiang, HUANG Tianyao, SHLEZINGER N, et al. Joint transmit beamforming for multiuser MIMO communications and MIMO radar[J]. IEEE Transactions on Signal Processing, 2020, 68: 3929–3944. doi: 10.1109/TSP.2020.3004739.
[11]	YANG Chenhao, WANG Xin, NI Wei, et al. Optimal beamforming for MIMO DFRC systems with transmit covariance constraints[J]. IEEE Transactions on Signal Processing, 2025, 73: 601–616. doi: 10.1109/TSP.2025.3529722.
[12]	LIU Fan, LIU Yafeng, LI Ang, et al. Cramér-rao bound optimization for joint radar-communication beamforming[J]. IEEE Transactions on Signal Processing, 2022, 70: 240–253. doi: 10.1109/TSP.2021.3135692.
[13]	WU Jiageng, WANG Zhiguo, LIU Yafeng, et al. Efficient global algorithms for transmit beamforming design in ISAC systems[J]. IEEE Transactions on Signal Processing, 2024, 72: 4493–4508. doi: 10.1109/TSP.2024.3457817.
[14]	WEN Cai, HUANG Yan, and DAVIDSON T N. Efficient transceiver design for MIMO dual-function radar-communication systems[J]. IEEE Transactions on Signal Processing, 2023, 71: 1786–1801. doi: 10.1109/TSP.2023.3275274.
[15]	YUAN Ye, WANG Yuankai, ZHONG Kai, et al. Unimodular waveform design for dual-function radar-communication systems under per-user MUI energy constraint[J]. IEEE Signal Processing Letters, 2024, 31: 1064–1068. doi: 10.1109/LSP.2024.3386469.
[16]	CHEN Li, WANG Zhiqin, DU Ying, et al. Generalized transceiver beamforming for DFRC with MIMO radar and MU-MIMO communication[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1795–1808. doi: 10.1109/JSAC.2022.3155515.
[17]	TSINOS C G, ARORA A, CHATZINOTAS S, et al. Joint transmit waveform and receive filter design for dual-function radar-communication systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(6): 1378–1392. doi: 10.1109/JSTSP.2021.3112295.
[18]	吴文俊, 唐波, 汤俊, 等. 杂波环境中雷达通信一体化系统波形设计算法研究[J]. 雷达学报, 2022, 11(4): 570–580. doi: 10.12000/JR22105. WU Wenjun, TANG Bo, TANG Jun, et al. Waveform design for dual-function radar-communication systems in clutter[J]. Journal of Radars, 2022, 11(4): 570–580. doi: 10.12000/JR22105.
[19]	WU Wenjun, TANG Bo, and WANG Xuyang. Constant-modulus waveform design for dual-function radar-communication systems in the presence of clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(4): 4005–4017. doi: 10.1109/TAES.2023.3234927.
[20]	WANG Yiran, HU Xiaoyan, LI Ang, et al. Symbol-scaling based interference exploitation in ISAC systems: From symbol level to block level[J]. IEEE Transactions on Wireless Communications, 2025, 24(3): 2451–2466. doi: 10.1109/TWC.2024.3521584.
[21]	LIU Rang, LI Ming, LIU Qian, et al. Dual-functional radar-communication waveform design: A symbol-level precoding approach[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(6): 1316–1331. doi: 10.1109/JSTSP.2021.3111438.
[22]	LIU Rang, LI Ming, LIU Qian, et al. Joint transmit waveform and receive filter design for dual-functional radar-communication systems[C]. 2022 - IEEE International Conference on Communications, Seoul, Korea, 2022: 5116–5121. doi: 10.1109/ICC45855.2022.9838990.
[23]	CUI Guolong, YU Xianxiang, CAROTENUTO V, et al. Space-time transmit code and receive filter design for colocated MIMO radar[J]. IEEE Transactions on Signal Processing, 2017, 65(5): 1116–1129. doi: 10.1109/TSP.2016.2633242.
[24]	ABSIL P A, MAHONY R, and SEPULCHRE R. Optimization Algorithms on Matrix Manifolds[M]. Princeton, USA: Princeton University Press, 2009. doi: 10.1515/9781400830244.(查阅网上资料,未找到本条文献页码信息,请补充).