Security and Reliability-Optimal Offloading for Mobile Edge Computing in Low-latency Industrial IoT
-
摘要: 在工业物联网(IIoT)场景下，移动边缘计算(MEC)在提供高可靠低时延通信(URLLC)服务的同时，需确保数据传输的安全性。针对多址接入MEC网络中存在潜在窃听者的物理层安全(PLS)增强问题，该文研究了通信与计算阶段的联合优化，以提升系统的整体安全性与可靠性。基于有限码长(FBL)理论，构建了通信阶段MEC服务器与窃听者之间的解码性能差异模型，并利用极值理论(EVT)分析计算阶段的延迟违规概率。在系统极端情况下，推导出端到端泄露错误概率(LFP)的闭式表达式，并将其作为衡量系统联合安全性与可靠性的关键指标。为最小化LFP，该文提出一种高效的资源分配优化算法。具体而言，为了平衡安全性与可靠性，设计一种满足时延约束的通信与计算阶段时间分配方案，并以两阶段时间为优化变量，构建联合优化问题。然而，由于变量间耦合且目标函数非凸，无法直接求解。因此，采用局部线性化与凸松弛技术对问题进行重构，并提出一种基于连续凸近似(SCA)的优化算法来求解。针对任务规模增大时算法收敛性下降的问题，该文提出一种加速SCA(A-SCA)算法。该算法通过分析问题结构，推导了系统最优可靠性对应时间分配策略的闭式表达式，并优化了初始点选择机制。仿真结果验证了所提算法的准确性、收敛性与适应性，同时揭示了安全性与可靠性之间的权衡关系。Abstract:
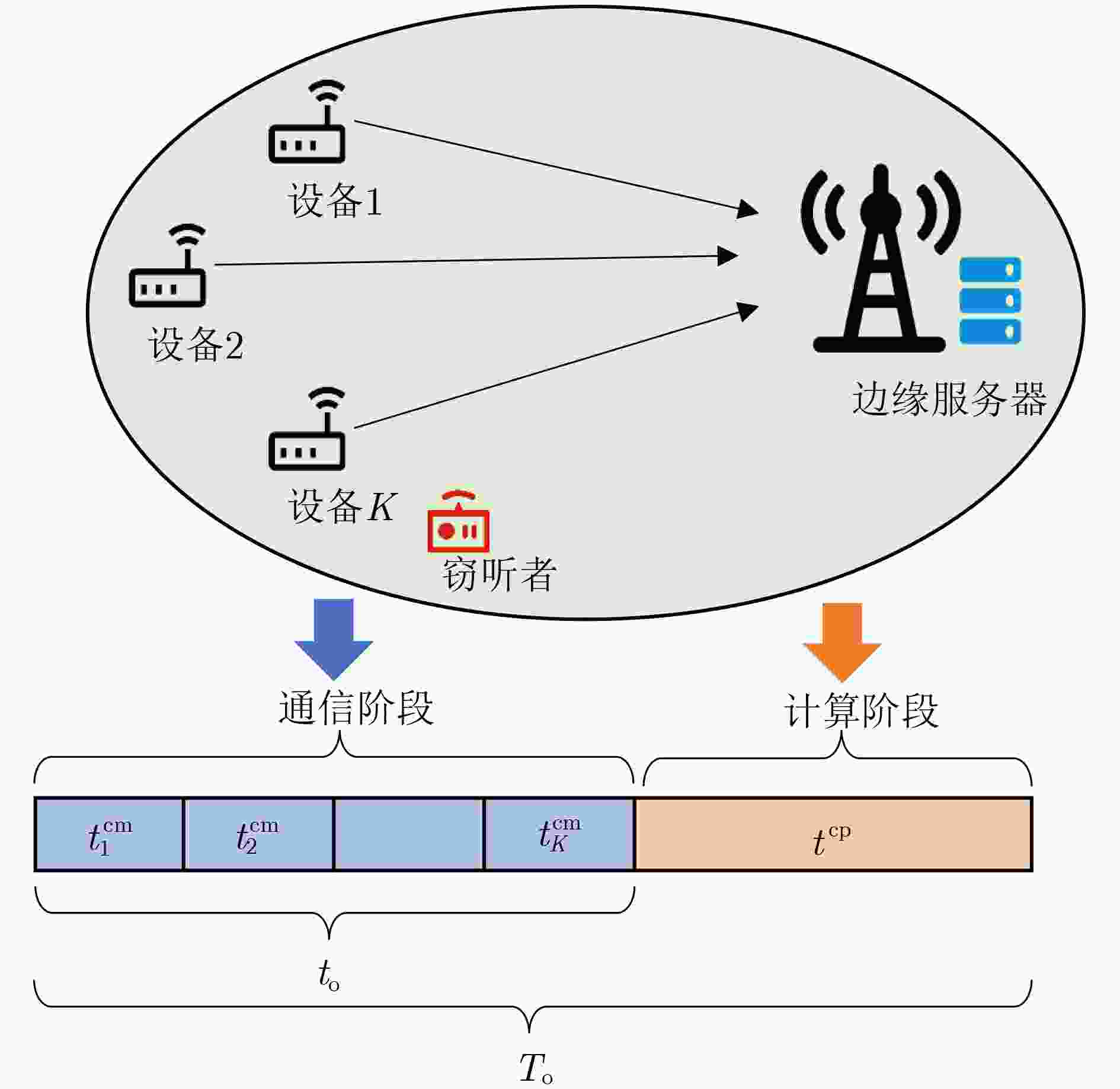
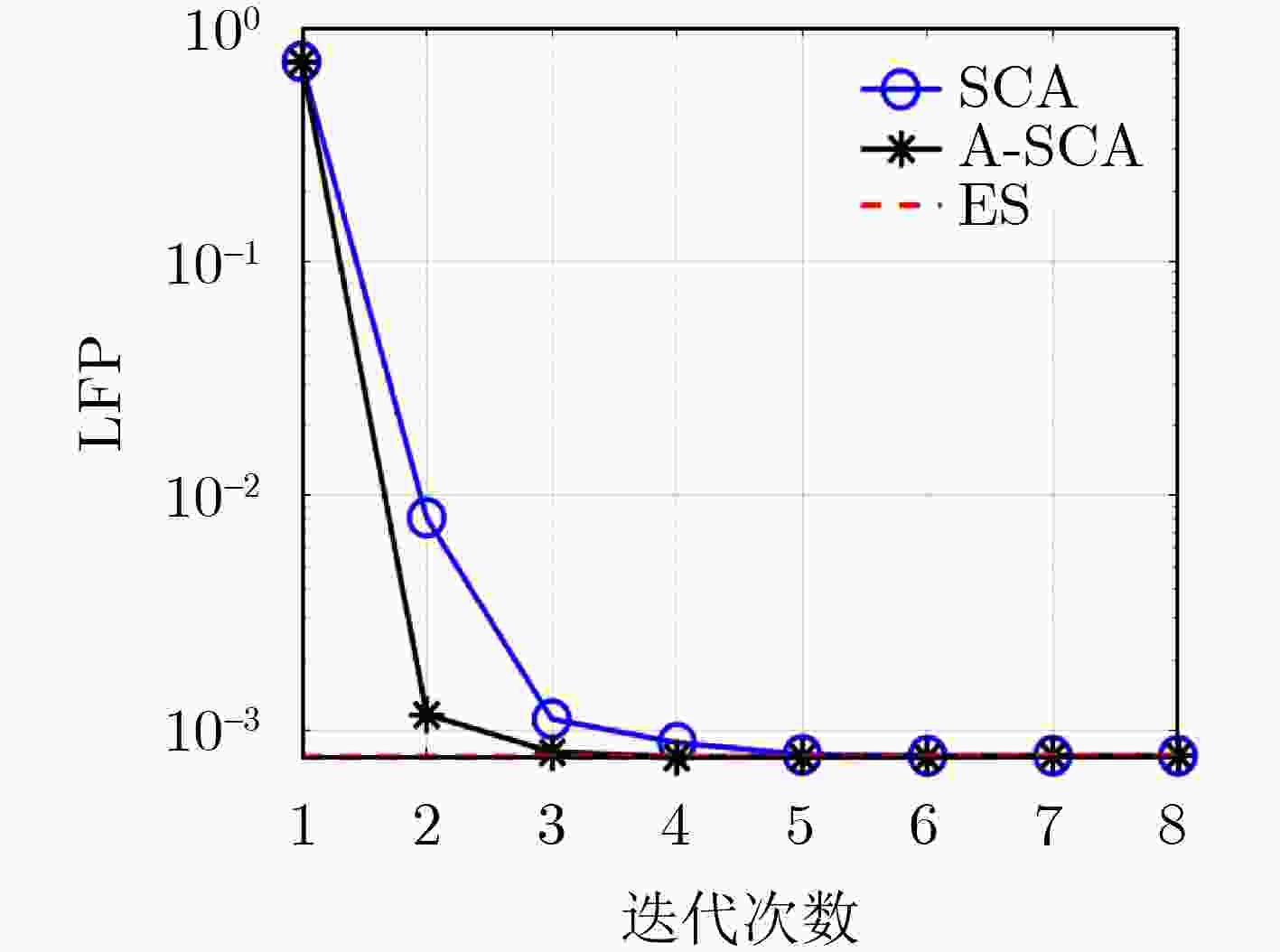
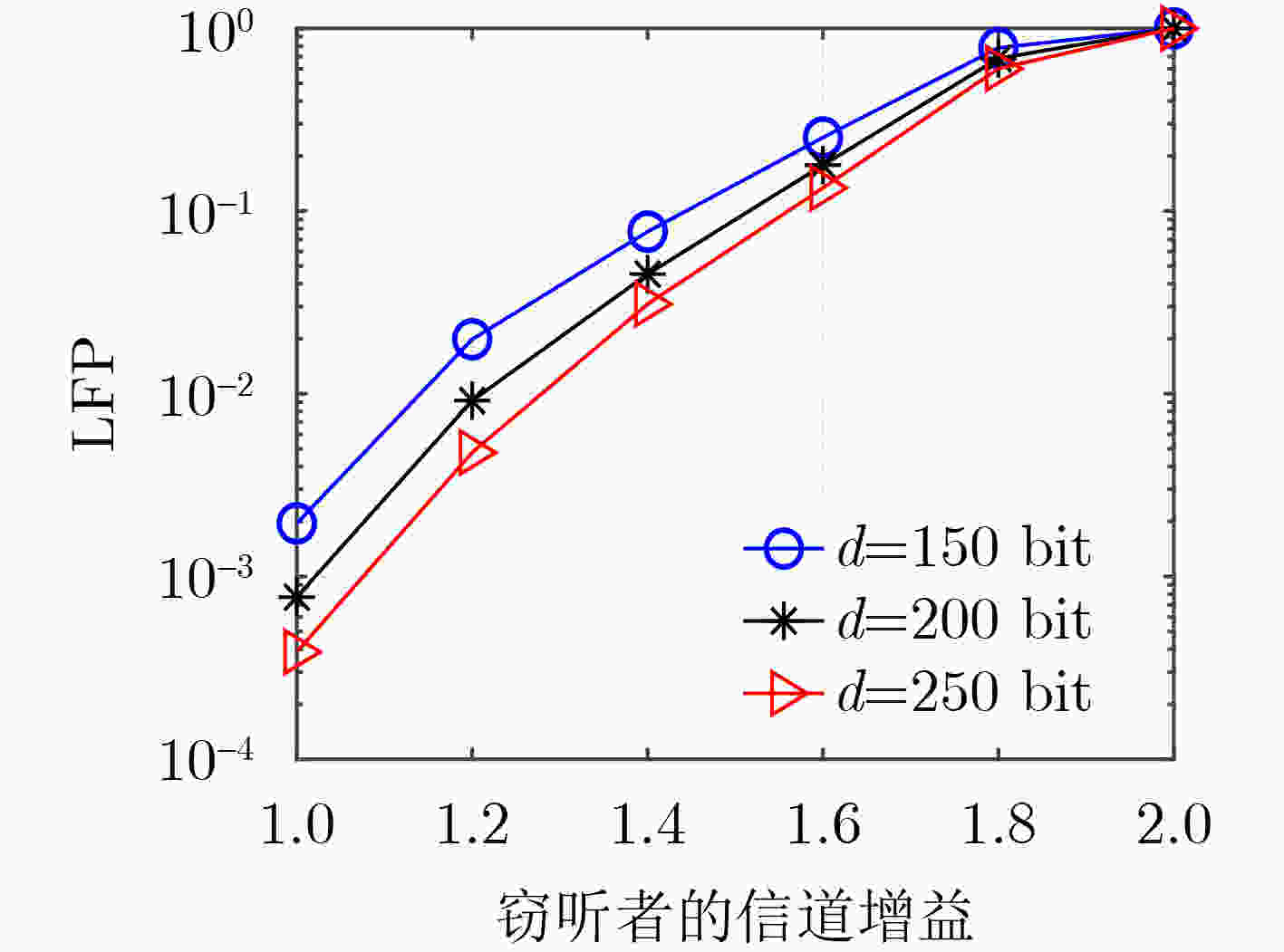
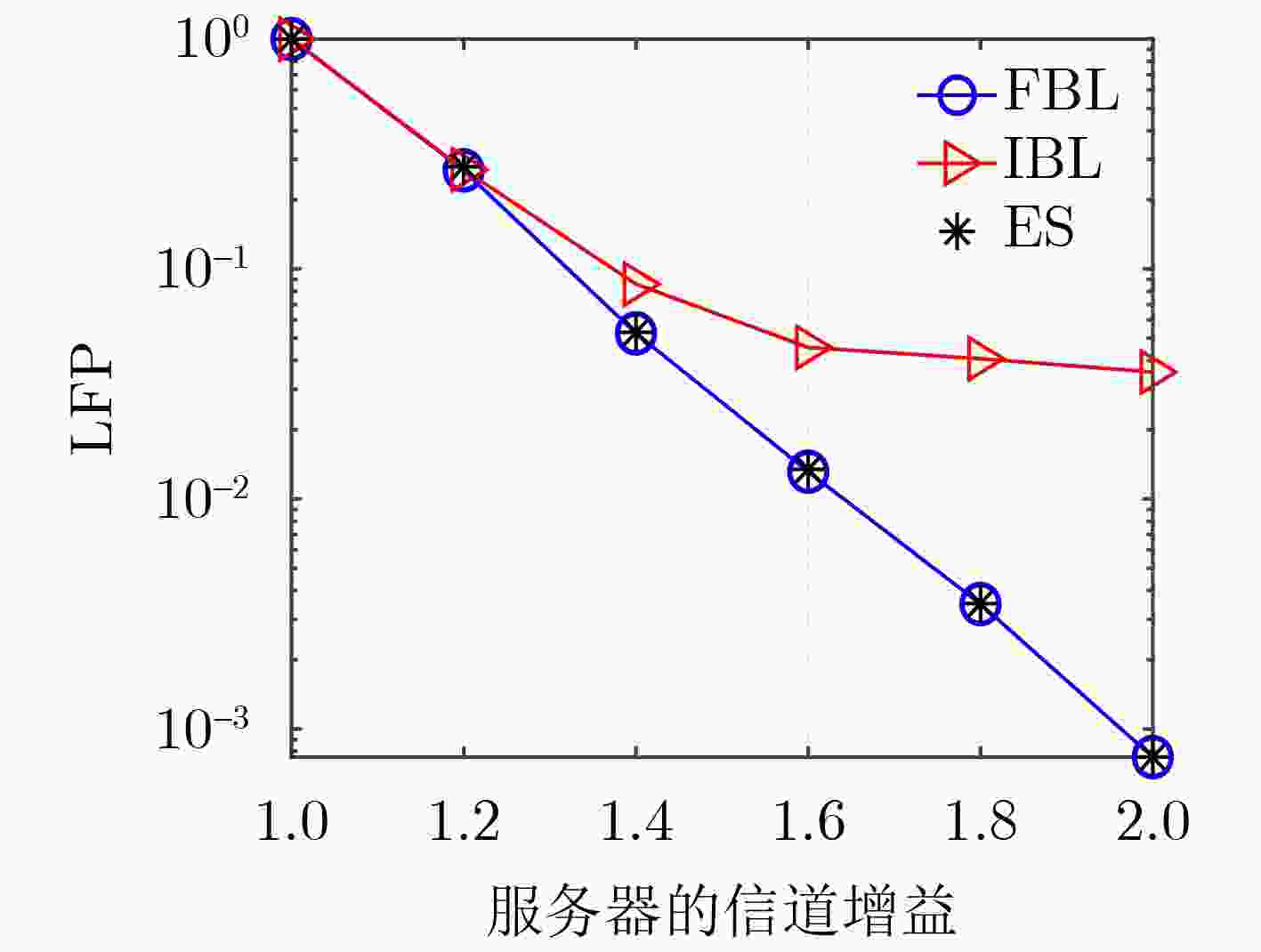
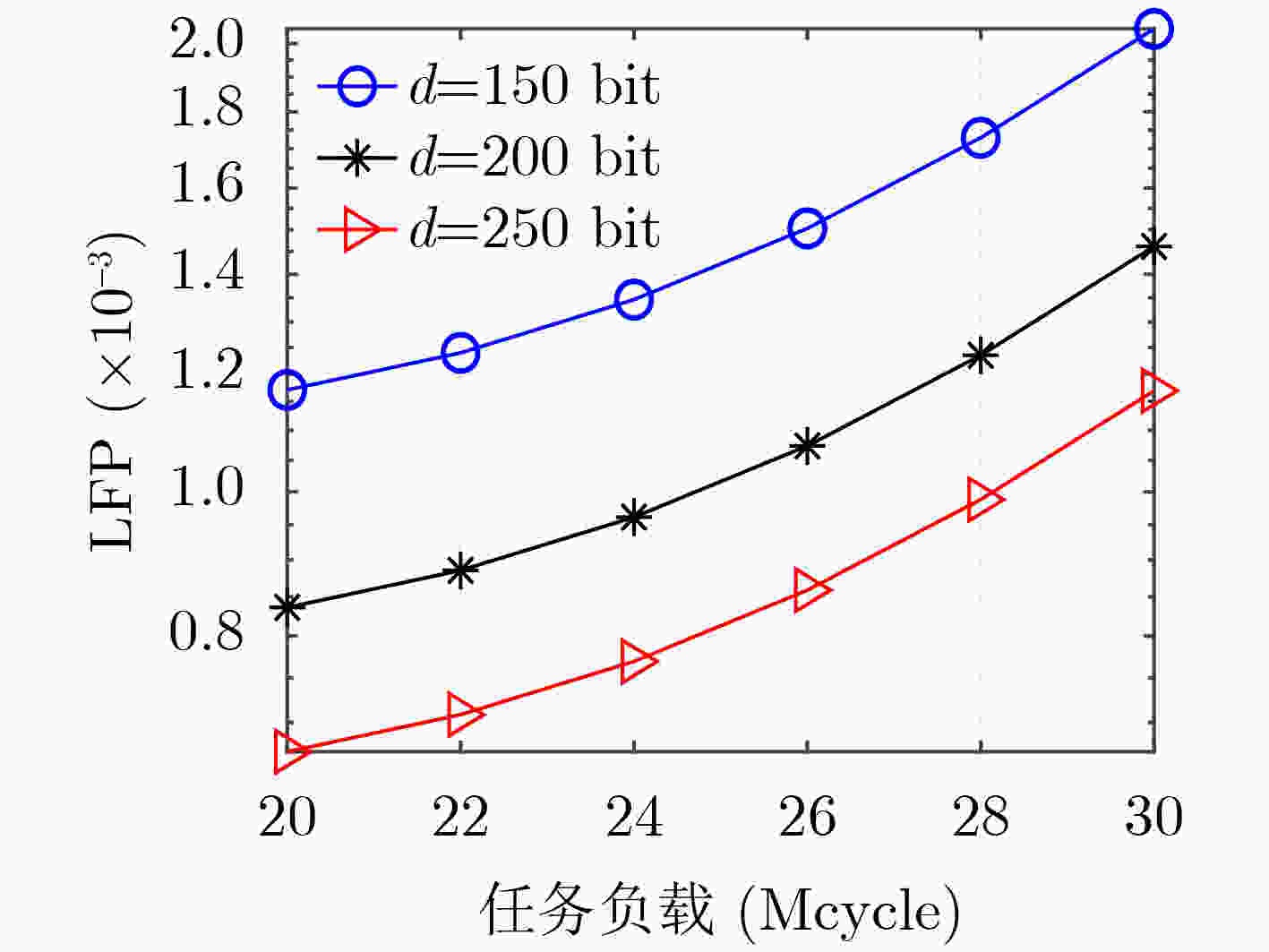
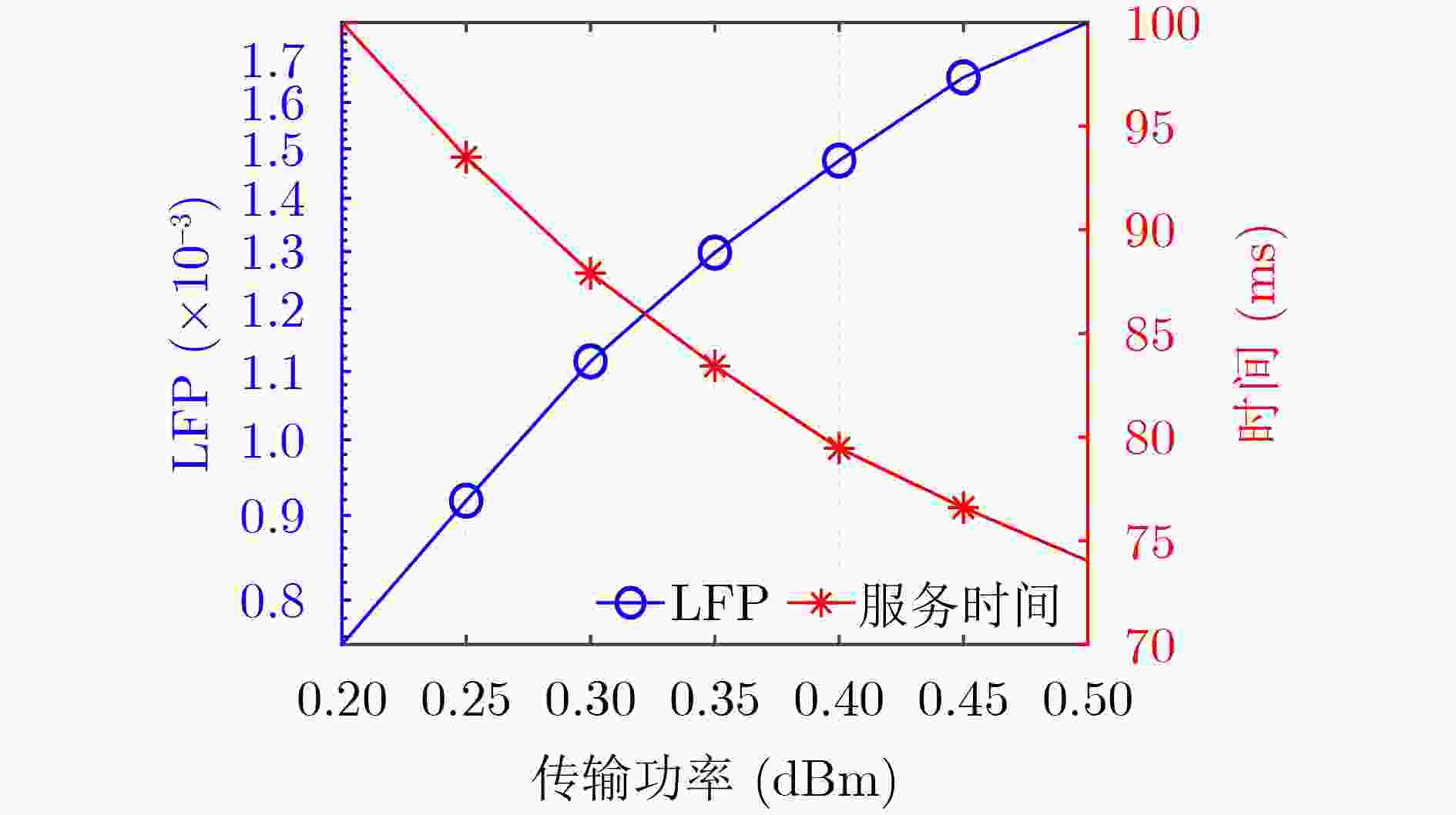
Objective With the advancement of Industry 4.0, the increasing demand for mission-critical and latency-sensitive applications is driving the evolution of Industrial Internet of Things (IIoT) networks. Mobile Edge Computing (MEC) has emerged as a key solution to alleviate the computational constraints of User Equipment (UE), thus enhancing IIoT system performance. However, ensuring high reliability and security remains a critical challenge in multi-access MEC networks. To support Ultra-Reliable and Low-Latency Communication (URLLC), short packet transmission is employed, introducing Finite BlockLength (FBL) effects that impacts communication performance. Additionally, queuing delays at the servers present a significant bottleneck in meeting latency requirement. While existing studies predominantly focus on secure transmission under the Infinite BlockLength (IBL) assumption, comprehensive investigations into Physical Layer Security (PLS) and reliability in the FBL regime remain scarce. To address this gap, this paper aims to jointly optimize the security and reliability of MEC networks. Specifically, an analytical expression for end-to-end Leakage Failure Probability (LFP) is derived to assess the security and reliability performance. Furthermore, an efficient two-phase time length allocation algorithm is proposed to enhance overall system performance. Methods This study examines the uplink URLLC scenario in a multi-access MEC network. First, leveraging FBL theory, the communication phase within frame structure is modeled, and the decoding error probabilities of both the server and the eavesdropper are characterized. Subsequently, Extreme Value Theory (EVT) is employed to model the delay violation probability in the computation phase. Based on these formulations, the end-to-end LFP is derived to comprehensively assess the system’s PLS and reliability. Given the stringent end-to-end latency constraints in URLLC, a fundamental trade-off between security and reliability arises. To investigate this trade-off, an optimization problem is formulated to minimize LFP while satisfying the latency constraint, with the time length of the communication and computation phases as the optimization variables. However, due to the presence of multiplicative non-convex Q-functions in the objective function, solving this optimization problem poses significant challenges. To overcome this, a local point expansion technique is employed to approximate the non-convex terms as summations, facilitating problem reformulation. Additionally, auxiliary variables are introduced to enable convex relaxation of the Q-functions, transforming the problem into a convex optimization framework. The reformulated problem is then efficiently solved using the Successive Convex Approximation (SCA) algorithm. In response to the issue of performance degradation in algorithm convergence when the task scale increases, an Accelerated-SCA (A-SCA) algorithm is introduced. By leveraging the problem structure, a closed-form expression for the time allocation strategy corresponding to the system's optimal reliability is derived, which improves the initial point selection mechanism. Finally, simulation results validate the accuracy, convergence, and adaptability of the proposed algorithm, while also revealing the trade-off between security and reliability. Results and Discussions The proposed FBL coding-based time allocation scheme is evaluated through numerical simulations to validate its effectiveness. A comparative analysis with the IBL coding-based scheme is conducted, demonstrating the performance gains achieved through the joint optimization of communication and computation phases, while highlighting the limitations of IBL coding. Furthermore, the quality of the sub-optimal solution obtained via the SCA algorithm is assessed by benchmarking against the exhaustive search method. Additionally, both constrained and unconstrained resource scenarios are considered to explore the trade-offs between security and reliability, as well as between time resource and LFP. First, ( Fig. 2 ) analyzes the convergence behavior of the proposed SCA-based time allocation scheme, demonstrating that the sub-optimal solution obtained closely approximates the global optimum. Furthermore, by optimizing the initial point selection with the A-SCA algorithm, the convergence speed and scalability are significantly enhanced. (Fig. 3 ) evaluates the variation of LFP with the eavesdropper’s channel gain under different task data sizes, revealing the fundamental trade-off between security and reliability, along with the associated performance compensation mechanism. (Fig. 4 ) illustrates the LFP trend as a function of the server’s channel gain, comparing the proposed scheme with IBL coding-based scheme. The results indicate that even in scenarios with low secure channel capacity, the proposed scheme achieves a 21.4% performance improvement, thereby validating its superiority in joint optimization across both phases. (Fig. 5 ) investigates the impact of task workload on LFP, while (Fig. 6 ) explores an unconstrained resource scenario, analyzing the influence of transmit power on LFP and the corresponding service time requirements.Conclusions This study explores the joint optimization of security and reliability in multi-access MEC networks supporting URLLC. In the FBL regime, the decoding error probability is modeled in the communication phase, while the delay violation probability is characterized using EVT in the computation phase. Based on these models, the LFP is derived as a key metric to quantify the system’s end-to-end PLS and reliability. Given the stringent latency constraints, a two-phase time length allocation optimization problem is formulated to minimize LFP, balancing security and reliability. To address the problem’s non-convexity, this paper first decouples the coupled variables through local linearization and reconstructs the problem. Next, convex upper and lower bounds of the complex Q-function are derived, enabling convex relaxation of the objective function. Subsequently, the SCA algorithm is applied iteratively to obtain a sub-optimal solution for the original problem. To tackle the issue of deteriorating convergence performance and increased complexity as the task scale grows, an A-SCA algorithm is proposed, which optimizes the initial point selection to address this challenge. Finally, simulation results validate the convergence, accuracy, and scalability of the proposed algorithm, demonstrating its performance advantages through comparison with existing approaches. Additionally, the impact of key system parameters on performance is systematically analyzed. The proposed LFP metric exhibits significant extensibility, being applicable to collaborative optimization of physical layer security and network layer security in URLLC systems, reliable task offloading in MEC, and throughput optimization in MIMO systems. Furthermore, the solution framework for LFP optimization problem, including problem decoupling and reconstruction, introduction of auxiliary variables for Q-function convex relaxation, iterative solving via SCA, and optimized initial point selection, provides valuable insights for solving multi-variable non-convex optimization problems in the FBL regime. -
1 基于连续凸近似的时间分配算法
输入：时间分配向量$ {\hat t_0} = (\hat t_1^{{\text{cm}}},\hat t_2^{{\text{cm}}}, \ldots ,\hat t_K^{{\text{cm}}},\hat t_{}^{{\text{cp}}}) $，迭代索引
$k = 0$以及收敛阈值${\mu _{{\text{th}}}}$；输出：系统最优通信与计算阶段时间分配策略
$ {t^*} = ({m^*}{T_{\text{s}}},{t^{{\text{cp*}}}}) $；(1) 根据$ {{\mathbf{\hat t}}_0} $和式(22)-式(25)，构建凸目标函数$ \varepsilon _{{\text{LF}}}^k \triangleq \hat \varepsilon _{{\text{LF}}}^k(t|{\hat t_0}) $； (2) 求解重构的凸优化问题${\mathcal{P}_2}$，得到该轮迭代最优时间分配方案
$ \hat t_k^* $；(3) 如果$ |\varepsilon _{{\text{LF}}}^k(\hat t_k^*) - \varepsilon _{{\text{LF}}}^{k - 1}(\hat t_{k - 1}^*)| \le {\mu _{{\text{th}}}} $，跳转到步骤(6)； (4) $\hat t_{k + 1}^{} = \hat t_k^*$，$k = k + 1$，跳转到步骤(2)； (5) 通过$m \triangleq (\hat t_1^{{\text{cm*}}},\hat t_2^{{\text{cm*}}}, \cdots ,\hat t_K^{{\text{cm*}}})/{T_{\text{s}}}$计算出非整数通信码长； (6) 根据式(28)，对各UE通信码长进行比较取整； (7) 得到原始问题${\mathcal{P}_1}$的有效解$ {t^*} = ({m^*}{T_{\text{s}}},{t^{{\text{cp*}}}}) $ 
下载: 导出CSV
2 基于加速型连续凸近似的高效时间分配算
输入：迭代索引$k = 0$以及收敛阈值${\mu _{{\text{th}}}}$； 输出：系统最优通信与计算阶段时间分配策略
$ {t^*} = (\hat t_1^{{\text{cm*}}},\hat t_2^{{\text{cm*}}}, \ldots ,\hat t_K^{{\text{cm*}}},\hat t_{}^{{\text{cp*}}}) $；(1) 根据式(31)-式(32)，构造优化问题${\mathcal{P}_4}$。根据目标函数关于自
变量单调递减特性，通过二分搜索方法求得最优$ {\hat t_1}^{{\text{cm*}}} $；(2) 根据解析表达式(35)，计算出问题${\mathcal{P}_3}$的最优解$ {\hat t^{{\text{cm*}}}} $； (3) 将$ {\hat t^{{\text{cm*}}}} $作为${\mathcal{P}_2}$迭代的起始点，即$ {\hat t_0} = {\hat t^{{\text{cm*}}}} $。 (4) 执行算法1。
下载: 导出CSV
-
[1] PELLE I, PAOLUCCI F, SONKOLY B, et al. Latency-sensitive edge/cloud serverless dynamic deployment over telemetry-based packet-optical network[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(9): 2849–2863. doi: 10.1109/JSAC.2021.3064655. [2] 王新奕, 费泽松, 周一青, 等. 面向物联网的通感算智融合: 关键技术与未来展望[J]. 电子与信息学报, 2025, 47(4): 888–908. doi: 10.11999/JEIT240806.WANG Xinyi, FEI Zesong, ZHOU Yiqing, et al. Integrated sensing, communication, computation, and intelligence towards IoT: Key technologies and future directions[J]. Journal of Electronics & Information Technology, 2025, 47(4): 888–908. doi: 10.11999/JEIT240806. [3] AL-TURJMAN F and ALTURJMAN S. Context-sensitive access in industrial internet of things (IIoT) healthcare applications[J]. IEEE Transactions on Industrial Informatics, 2018, 14(6): 2736–2744. doi: 10.1109/TII.2018.2808190. [4] MAO Yuyi, YOU Changsheng, ZHANG Jun, et al. A survey on mobile edge computing: The communication perspective[J]. IEEE Communications Surveys & Tutorials, 2017, 19(4): 2322–2358. doi: 10.1109/COMST.2017.2745201. [5] DILLON T, WU Chen, and CHANG E. Cloud computing: Issues and challenges[C]. Proceedings of 2010 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, WA, Australia, 2010: 27–33. doi: 10.1109/AINA.2010.187. [6] SUN Gang, WANG Zhiying, SU Hanyu, et al. Profit maximization of independent task offloading in MEC-enabled 5G internet of vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(11): 16449–16461. doi: 10.1109/TITS.2024.3416300. [7] ZHONG Liang, LIU Yuyang, DENG Xianjun, et al. Distributed optimization of multi-role UAV functionality switching and trajectory for security task offloading in UAV-assisted MEC[J]. IEEE Transactions on Vehicular Technology, 2024, 73(12): 19432–19447. doi: 10.1109/TVT.2024.3434354. [8] SAUTER T and TREYTL A. IoT-enabled sensors in automation systems and their security challenges[J]. IEEE Sensors Letters, 2023, 7(12): 7500904. doi: 10.1109/LSENS.2023.3332404. [9] RANAWEERA P, JURCUT A D, and LIYANAGE M. Survey on multi-access edge computing security and privacy[J]. IEEE Communications Surveys & Tutorials, 2021, 23(2): 1078–1124. doi: 10.1109/COMST.2021.3062546. [10] DING Yu, ZHANG Qingqing, LU Weidang, et al. Collaborative communication and computation for secure UAV-enabled MEC against active aerial eavesdropping[J]. IEEE Transactions on Wireless Communications, 2024, 23(11): 15915–15929. doi: 10.1109/TWC.2024.3435017. [11] MACH P and BECVAR Z. Mobile edge computing: A survey on architecture and computation offloading[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628–1656. doi: 10.1109/COMST.2017.2682318. [12] SHE Changyang, PAN Cunhua, DUONG T Q, et al. Guest editorial xURLLC in 6G: Next generation ultra-reliable and low-latency communications[J]. IEEE Journal on Selected Areas in Communications, 2023, 41(7): 1963–1968. doi: 10.1109/JSAC.2023.3282543. [13] FENG Chen, WANG Huiming, and POOR H V. Reliable and secure short-packet communications[J]. IEEE Transactions on Wireless Communications, 2022, 21(3): 1913–1926. doi: 10.1109/TWC.2021.3108042. [14] WANG Huiming, YANG Qian, DING Zhiguo, et al. Secure short-packet communications for mission-critical IoT applications[J]. IEEE Transactions on Wireless Communications, 2019, 18(5): 2565–2578. doi: 10.1109/TWC.2019.2904968. [15] KOSTINA V and VERDU S. Fixed-length lossy compression in the finite blocklength regime[J]. IEEE Transactions on Information Theory, 2012, 58(6): 3309–3338. doi: 10.1109/TIT.2012.2186786. [16] KOSTINA V and VERDÚ S. Lossy joint source-channel coding in the finite blocklength regime[J]. IEEE Transactions on Information Theory, 2013, 59(5): 2545–2575. doi: 10.1109/TIT.2013.2238657. [17] CAO M X, RAMAKRISHNAN N, BERTA M, et al. Channel simulation: Finite blocklengths and broadcast channels[J]. IEEE Transactions on Information Theory, 2024, 70(10): 6780–6808. doi: 10.1109/TIT.2024.3445998. [18] POLYANSKIY Y, POOR H V, and VERDU S. Channel coding rate in the finite blocklength regime[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2307–2359. doi: 10.1109/TIT.2010.2043769. [19] HU Yulin, ZHU Yao, GURSOY M C, et al. SWIPT-enabled relaying in IoT networks operating with finite blocklength codes[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(1): 74–88. doi: 10.1109/JSAC.2018.2872361. [20] ZHU Yao, HU Yulin, SCHMEINK A, et al. Energy minimization of mobile edge computing networks with HARQ in the finite blocklength regime[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 7105–7120. doi: 10.1109/TWC.2022.3154670. [21] YANG Helin, XIONG Zehui, ZHAO Jun, et al. Deep reinforcement learning based massive access management for ultra-reliable low-latency communications[J]. IEEE Transactions on Wireless Communications, 2021, 20(5): 2977–2990. doi: 10.1109/TWC.2020.3046262. [22] YU Xinlan, ZHU Yao, HU Yulin, et al. Blocklength allocation for security-enhanced MEC with dependency-aware tasks[C]. Proceedings of 2023 International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2023: 761–766. doi: 10.1109/WCSP58612.2023.10404666. [23] BENNIS M, DEBBAH M, and POOR H V. Ultrareliable and low-latency wireless communication: Tail, risk, and scale[J]. Proceedings of the IEEE, 2018, 106(10): 1834–1853. doi: 10.1109/JPROC.2018.2867029. [24] SAMARAKOON S, BENNIS M, SAAD W, et al. Distributed federated learning for ultra-reliable low-latency vehicular communications[J]. IEEE Transactions on Communications, 2020, 68(2): 1146–1159. doi: 10.1109/TCOMM.2019.2956472. [25] LIU Chenfeng, BENNIS M, DEBBAH M, et al. Dynamic task offloading and resource allocation for ultra-reliable low-latency edge computing[J]. IEEE Transactions on Communications, 2019, 67(6): 4132–4150. doi: 10.1109/TCOMM.2019.2898573. [26] MAO Bomin, LIU Jiajia, WU Yingying, et al. Security and privacy on 6G network edge: A survey[J]. IEEE Communications Surveys & Tutorials, 2023, 25(2): 1095–1127. doi: 10.1109/COMST.2023.3244674. [27] ILLI E, QARAQE M, ALTHUNIBAT S, et al. Physical layer security for authentication, confidentiality, and malicious node detection: A paradigm shift in securing IoT networks[J]. IEEE Communications Surveys & Tutorials, 2024, 26(1): 347–388. doi: 10.1109/COMST.2023.3327327. [28] SOLAIJA M S J, SALMAN H, and ARSLAN H. Towards a unified framework for physical layer security in 5G and beyond networks[J]. IEEE Open Journal of Vehicular Technology, 2022, 3: 321–343. doi: 10.1109/OJVT.2022.3183218. [29] HE Xiaofan, JIN Richeng, and DAI Huaiyu. Physical-layer assisted secure offloading in mobile-edge computing[J]. IEEE Transactions on Wireless Communications, 2020, 19(6): 4054–4066. doi: 10.1109/TWC.2020.2979456. [30] BAI Tong, WANG Jingjing, REN Yong, et al. Energy-efficient computation offloading for secure UAV-edge-computing systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(6): 6074–6087. doi: 10.1109/TVT.2019.2912227. [31] XU Jie and YAO Jianping. Exploiting physical-layer security for multiuser multicarrier computation offloading[J]. IEEE Wireless Communications Letters, 2019, 8(1): 9–12. doi: 10.1109/LWC.2018.2845882. [32] ZHU Yao, YUAN Xiaopeng, HU Yulin, et al. Trade reliability for security: Leakage-failure probability minimization for machine-type communications in URLLC[J]. IEEE Journal on Selected Areas in Communications, 2023, 41(7): 2123–2137. doi: 10.1109/JSAC.2023.3280960. [33] ZHU Yao, HU Yulin, YANG Tianyu, et al. Reliability-optimal offloading in low-latency edge computing networks: Analytical and reinforcement learning based designs[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 6058–6072. doi: 10.1109/TVT.2021.3073791. [34] ZHAO Xiaoyu, CHEN Wei, and POOR H V. Achieving extremely low-latency in industrial internet of things: Joint finite blocklength coding, resource block matching, and performance analysis[J]. IEEE Transactions on Communications, 2021, 69(10): 6529–6544. doi: 10.1109/TCOMM.2021.3097727. [35] SHI Chenhao, HU Yulin, ZHU Yao, et al. Security-aware energy-efficient design for mobile edge computing network operating with finite blocklength codes[J]. EURASIP Journal on Wireless Communications and Networking, 2024, 2024(1): 67. doi: 10.1186/s13638-024-02395-z. -
图(6) / 表(2)
计量
- 文章访问数: 57
- HTML全文浏览量: 39
- PDF下载量: 4
- 被引次数: 0
下载:
